FTN系统中两种频域迭代分组判决反馈均衡器仿真分析

张广娜,郭明喜,沈越泓

(解放军理工大学 通信工程学院,南京 210007)

0 概述

1975年,Mazo首次提出了超奈奎斯特(Faster-than-Nyquist,FTN)理论[1],并指出FTN码元速率传输体系在相同带宽、相同比特能量、相同误码率性能的条件下,可以比传统的Nyquist体系多传输30%以上的数据符号[2]。因此,在频谱资源紧缺的当今社会,FTN受到人们更广泛的关注。然而,FTN提高通信系统的传输速率是以接收端引入无限长的码间串扰为代价,如何以较低的计算复杂度来消除码间串扰成为FTN信号研究中非常重要的课题。

目前,人们已经提出了一系列FTN系统接收端的解调算法,其中,Forney和Hayes分别提出了最大似然序列估计[3]和维特比算法[4],但其复杂度随滤波器抽头系数和每符号所包含比特数的增加呈指数增长。文献[5]提出了一种基于矩阵分解的判决反馈均衡算法,其误码率性能优于维特比算法,但矩阵的正交三角(QR)分解使其计算复杂度仍很高。其他复杂度相对较低的接收算法也被引入到FTN系统中,如连续干扰消除算法[6]、加窗Chase均衡[7]。这里提到的接收算法均为基于时域均衡的操作,在码间串扰无限长的FTN系统中的解调复杂度都很高。

相比时域均衡,频域均衡操作可以在保持系统误码率性能不变的前提下有效降低计算复杂度[8],且非线性均衡器消除码间串扰的性能优于线性均衡器[9-10]。线性频域均衡器(Frequency-Domain Equalizer,FDE)[11-12]和迭代分组判决反馈均衡器(Iterative Block Decision Feedback Equalizer,IBDFE)[13-14]均为复杂度较低的频域均衡算法。为进一步降低复杂度,文献[15]提出了将判决信号中的误差与期望信号分离的低复杂度IBDFE(LC-IBDFE)算法。FTN系统中频域均衡器的研究都是在AWGN信道条件下,实际应用中,通信系统很少处于理想的AWGN信道条件。为进一步推进FTN接收理论的实用化,本文将复杂度较低的IBDFE和LC-IBDFE接收算法扩展到频率选择性衰落信道,并仿真验证其可行性,分析两者的误码率性能。

1 FTN系统模型

普通二进制调制信号的基带形式为:

(1)

信号经过AWGN信道并采样得到序列:

(2)

式(2)的第1项为发送符号相关项,第2项代表FTN系统中的码间串扰。为方便接收端的有限长均衡器操作,需要对无限长ISI做近似截短处理,截短后的ISI长度是L[16]。当通信系统为传统Nyquist传输系统,即τ=1时,第2项为0。对于已有的FTN-FDE算法,发送端将数据分割成独立的数据块并加上长度为Lcp的循环前缀(CP)。分别取出数据块的前Lcp/2和后Lcp/2位符号,得到的接收数据块为:

yk=[y0,y1,…,yN-1]T=Ga+n

(3)

其中,a=[a0,a1,…,aN-1]T为发送数据块,n=[η0,η1,…,ηN-1]T为噪声向量,矩阵G代表码间串扰,该矩阵为循环矩阵[11]。

2 低复杂度频域迭代分组判决反馈均衡器

2.1 IBDFE算法

已有的IBDFE结构简图如图1所示。

图1 IBDFE结构简图

由图1可得,IBDFE由前馈滤波器和反馈滤波器两部分组成。在发送信号分组前,发送端首先发送一已知的长度为n的PN序列{qm},之后在长为(P-n)的数据分组{dm}后增加PN序列{qm}。为避免相邻分组内的数据符号相互干扰,PN序列长度需满足n≥(L-1)/2,即不小于码间串扰的长度。

发送数据块经过AWGN信道并经匹配滤波和抽样后得到信号序列{xi},其经过FFT变换得到:

Xp=HpSp+Wp

(4)

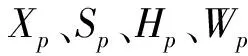
(5)

文献[13]给出该均衡器的反馈抽头系数是:

(6)

(7)

前馈抽头系数是:

(8)

2.2 LC-IBDFE算法

(9)

(10)

根据Parseval定理:

(11)

其中:

将式(9)代入式(11)中,得:

(12)

2.3 频率选择性衰落信道下的仿真实验

上述2种适用于FTN系统的频域均衡器都是基于AWGN信道条件的,但在实际应用中,通信系统很少处于这种理想的信道条件下。为了进一步推进FTN的实用化,本文将2种频域均衡器扩展到频率选择性衰落信道,讨论其可行性,分析其误码率性能。

(13)

当循环前缀序列足够长时,该系统模型可以写成类似于式(3)的矩阵形式,且干扰矩阵仍为一循环矩阵[11],因此,上述2种AWGN信道下的频域均衡器适用于频率选择性衰落信道。

3 仿真实验与结果

下面通过仿真实验验证IBDFE和LC-IBDFE在频率选择性衰落信道中的可行性,并分析其误码率性能。二进制FTN通信系统采用根升余弦成型脉冲,脉冲滚降系数为α=0.3,加速因子τ取0.8,频率选择性衰落信道的有效路径数,每条路径包络服从瑞利分布。数据块长度为1 024,PN序列长度为12,满足Lpn≥(L+2(Lch-1))/2,最大迭代次数为NI=3。对于IBDFE,β=4,Ps,pre=0.1。

图2、图3给出了在2种信道下IBDFE和LC-IBDFE的性能比较情况,其中,α=0.3,τ=0.8,NI=3。可以看出,在频率选择性衰落信道中,IBDFE和LC-IBDFE的误码率性能较AWGN信道中的性能均有所下降,且在衰落信道中,两者的性能十分接近。

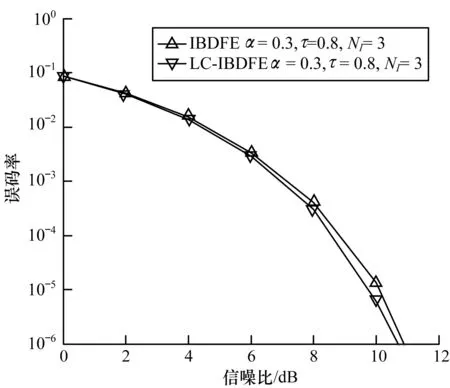
图2 AWGN信道下IBDFE、LC-IBDFE的性能比较

图3 频率选择性衰落信道下IBDFE、LC-IBDFE的性能比较

由仿真结果可知,将2种频域均衡器扩展到频率选择性衰落信道是可行的,且在多径数目不大的情况下,误码率性能与AWGN信道条件下的性能相比变化很小。但是随着多径数目的增加,码间串扰将越来越严重,FTN系统性能会越来越差。为减少ISI对相邻数据块的影响,ISI长度越长,所用的PN序列长度也要越长,但PN序列并非有效信息,这会导致有效信息速率降低,从而使FTN通信系统逐渐失去优势。

4 结束语

为了将FTN接收理论进一步向实用化推进,本文将FTN系统中的低复杂度频域迭代分组判决反馈均衡器扩展到频率选择性衰落信道中,并仿真验证了其可行性。结果表明,在频率选择性衰落信道中,适当增加PN序列的长度,IBDFE和LC-IBDFE接收算法仍可以检测出FTN信号。但PN序列长度随频率选择性衰落信道多径数目的增加而增加,与AWGN信道条件相比,有效信息的速率会逐渐下降,因此,下一步将研究如何选择适当的PN序列长度。

[1] MAZOJ E.Faster-than-Nyquist Signaling[J].Bell System Technical Journal,1975,54(8):1451-1462.

[2] 童 莹,郭明喜,沈越泓.超Nyquist传输技术专题讲座(一)第2讲 超Nyquist传输系统概述[J].军事通信技术,2014,35(4):633-635.

[3] FORNEY G D.Maximum-likelihood Sequence Estimation of Digital Sequences in The Presence of Inter-symbol Inter-ference[J].IEEE Transactions on Information Theory,1972,IT-18(3):363-378.

[4] HAYES J F.The Viterbi Algorithm Applied to Digital Data Transmission[J].IEEE Communication Magazine,2002,40(5):26-32.

[5] BAEK M S,HUR N H,LIM H.Novel Interference Cancellation Technique Based on Matrix Computation for FTN Communication System[C]//Proceedings of IEEE Military Communications Conference.Washington D.C.,USA:IEEE Press,2014:830-834.

[6] RUSEK F,ANDERSON J.Multistream Faster than Nyquist Signaling[J].IEEE Transactions on Communication,2009,57(5):1329-1340.

[7] LI Hui,SHEN Yuehong,XU Kun.Windows Fast Chase Detection for Long Intersymbol Interference Channels[J].Frequenz,2010,64(7-8):134-139.

[8] BENVENUTO N,DINIS R,FALCONER D,et al.Single Carrier Modulation with Nonlinear Frequency Domain Equalization:An Idea Whose Time Has Come Again[J].Proceedings of the IEEE,2010,98(1):69-96.

[9] SALZ J.Optimum Mean-square Decision Feedback Equalization[J].Bell System Technical Journal,1973,52(8):1341-1373.

[10] 郭明喜,沈越泓,聂 勇,等.一种基于两级均衡的超Nyquist码元速率信号传输实现方案[J].电路与系统学报,2013,18(2):119-122.

[11] SUGIURA S.Frequency-domain Equalization of Faster-than-Nyquist Signaling[J].IEEE Wireless Communica-tions Letters,2013,2(5):555-558.

[12] 刘顺兰,刘小云,刘婷婷.基于Turbo信道编码的SC-FDE系统[J].计算机工程,2010,36(7):270-272.

[13] ZHANG Chao,WANG Zhaocheng,PAN Changyong,et al.Low-complexity Iterative Frequency Domain Decision Feedback Equalization[J].IEEE Transactions on Vehicular Technology,2011,60(3):1295-1301.

[14] TOMASIN S,BENVENUTO N.Fractionally Spaced Non-linear Equalization of Faster-than-Nyquist Signals[C]//Proceedings of the 22nd European Signal Processing Con-ference.Washington D.C.,USA:IEEE Press,2014:1861-1865.

[15] XU Yang,GUO Mingxi,SHEN Yuehong,et al.A Low Complexity Iterative Frequency Domain Decision Feedback Equalization of Faster than Nyquist Signals[J].Com-munications Technology,2015,48(8):880-885.

[16] JOHN B A,RUSEK F,OWALL V.Faster-than-Nyquist Signaling[J].Proceedings of the IEEE,2013,101(8):23-35.