基于改进FCLS 算法的南极海冰密集度估算及算法比较

宋翔宇 刘婷婷 王泽民 刘艳霞

(1武汉大学中国南极测绘研究中心,湖北 武汉 430079;2武汉市测绘研究院,湖北 武汉 430022)

0 引言

海冰处于海水与大气的交界面,具有良好的热力隔绝效应,它通过影响海洋和大气的热交换进而影响全球的气候变化[1]。海冰密集度是指给定区域面积内海冰所占比例,是极区海冰研究的重要指标之一。随着遥感技术的快速发展,越来越多的数据可用于海冰密集度监测。目前,可用于海冰密集度估算的数据包括光学影像数据[2-3]、合成孔径雷达(synthetic aperture radar,SAR)数据[4]和被动微波数据[5]。其中,光学影像受云雨和极夜的影响,可用于极区的数据非常有限; SAR影像数据[4]受电磁波的入射角度和频率的影响,数据质量难以保证,同时受到影像幅宽限制,一天之内较难获得覆盖全南极的影像数据; 被动微波数据分辨率较低,但不受云雨等的影响,且覆盖范围广,可全天候获取大范围地表信息。因此,被动微波数据被广泛应用于海冰密集度的估算及应用中。

目前基于被动微波数据估算海冰密集度的算法[6]主要包括 NORSEX[7]、Bootstrap[8]、NASA Team(NT)[9]、NASA Team2(NT2)[10]、ARTIST Sea Ice(ASI)[11-12]等。根据算法所使用的被动微波数据频段的差异,可以将以上算法分为基于低频(19 GHz和 37 GHz)数据的算法和基于高频(89 GHz)数据的算法。其中,NORSEX、Bootstrap和NT均为基于低频数据的算法,该类算法使用空间分辨率较低的低频数据,仅获得空间分辨率为25 km的海冰密集度结果; NT2和ASI均为基于高频数据的算法,这两种算法可获得较高空间分辨率的海冰密集度结果,但由于高频数据易受水汽的影响从而影响NT2和ASI等算法的精度[6]。与ASI相比,NT2算法通过给前向辐射传输模型设置不同的大气条件,获得不同海冰密集度下的亮温值,从而建立模拟观测样本的数据库,但随着气候环境的变化,模型的误差逐年变化,估算精度难以保证。基于全约束最小二乘法(fully constrained least squares,FCLS)的海冰密集度估算方法[13]通过将噪声引入海冰密集度估算方程,并结合约束项利用最小二乘法获得多种类型海冰的密集度的最优解。由于该算法仅使用19 GHz和37 GHz的低频数据,仅可获得空间分辨率为25 km的海冰密集度数据。为实现高空间分辨率多类型海冰密集度的估算,本文结合 NT2算法,提出一种融合亮温极化梯度率和光谱梯度率的基于 FCLS的海冰密集度估算方法(后文简称为“改进的方法”)。为验证算法精度,以日平均南极海冰过程与气候计划[14](Antarctic Sea Ice Processes and Climate,ASPeCt)船测数据为实测海冰密集度数据,利用均方差(root mean square error,RMSE)和偏差(bias)评定并对比改进的方法、NT2和ASI算法结果精度。

1 数据

1.1 AMSR-E

AMSR-E(The Advanced Microwave Scanning Radiometer for EOS)数据[15]自 2002年起可由Aqua卫星上搭载的被动微波传感器收集获得。该数据包括 6.9 GHz、10.7 GHz、18.7 GHz、23.8 GHz、36.5 GHz和89.0 GHz这6个频段,各频段均由垂直极化和水平极化两个通道组成,空间分辨率从5.4 km(89 GHz)—56 km(6.9 GHz)不等。与SMMR、SSM/I以及 SSMIS被动微波数据相比,AMSR-E具有多通道、高分辨率等优势。本研究使用了美国国家冰雪数据中心发布的19 GHz、37 GHz和89 GHz AMSR-E数据,空间分辨率均为12.5 km。

1.2 ASPeCt

ASPeCt[14]数据由南极研究科学委员会(Scientific Committee on Antarctic Research,SCAR)提供,由专业人员通过1980—2005年间的83次航海和2次航拍获得。该数据在海冰密集度低于 70%的区域低于实际值,误差在 10%—20%;随着海冰密集度的升高,误差可缩小为5%—10%;当海冰密集度达到90%—100%后,误差达到最小值。AMSR-E数据与ASPeCt船测数据仅在2002—2005年存在交集部分,因此本文利用 ASPeCt船测数据2002—2005年间的813个船测点,对应点海冰密集度及位置分布如图1所示。

2 海冰密集度估算方法

2.1 基于FCLS的海冰密集度估算方法

给定区域面积内海域可由开阔水域、一年冰和多年冰组成,因此海冰密集度估算方程如式(1)所示,表明被动微波数据中任一像元的亮温TB也可由开阔水域、一年冰和多年冰表述。

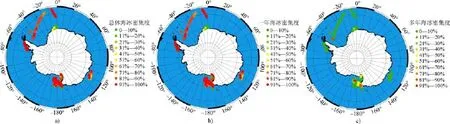
图1 ASPeCt船测数据分布图.a)总体海冰密集度; b) 一年冰海冰密集度; c) 多年冰海冰密集度Fig.1.ASPeCt ship survey data distribution map.a)total sea ice concentration; b)first-year ice concentration; c) multi-year iceconcentration

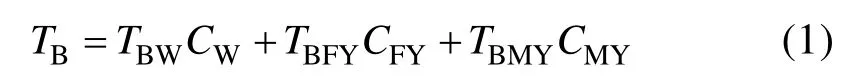
其中,TBW、TBFY和TBMY分别代表开阔水域、一年冰和多年冰参考亮温,CW、CFY和CMY分别表示开阔水域、一年冰和多年冰所占比例。

然而,该方程并未考虑各种误差所带来的影响。实际中,许多因素都将引起误差,如被动微波辐射计传感器带来的误差、微波辐射传输过程带来的误差和影像成像带来的误差等。因此,基于FCLS的海冰密集度估算方法通过引入误差系数n,获得高精度的多类型海冰的密集度结果[13]。基于此,式(1)可扩展为式(2):

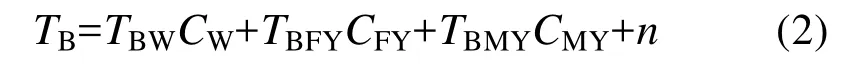
2.2 NT2

NT2算法首先通过给前向辐射传输模型设置不同的大气条件,获得不同海冰密集度下的亮温值,从而建立模拟观测样本的数据库,计算获得PRR(19)、PRR(89)和ΔGR。由影像实测亮温值计算影像极化梯度率PR和光谱梯度率GR,并在模型中搜索离真实观测样本最近的模拟样本,即(δR)最小时对应的海冰密集度及相应海冰类型。计算公式为式(3)—式(6):

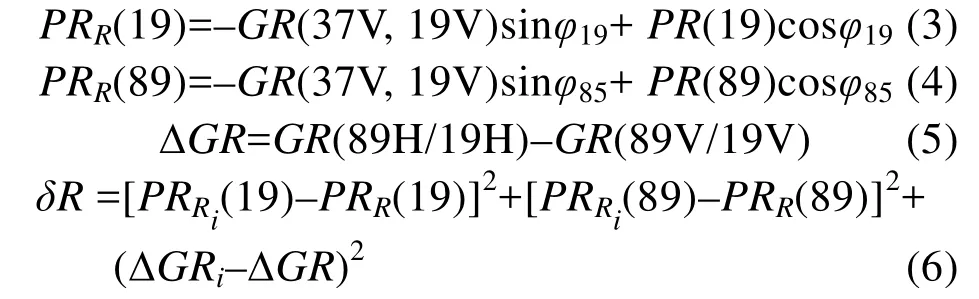
其中,PR是亮温的极化梯度率,GR表示光谱梯度率,PRRi是由影像实测亮温值计算得到的极化梯度率,ΔGRi由影像实测亮温值计算得到的光谱梯度率,计算公式同式(4)和式(5)。PRR(19)削弱了地表分层以及粗糙度对亮温的影响,PRR(89)可以消除海冰密集度变化和大气情况变化之间的不确定性,ΔGR解决了低海冰密集度与被探测表面起伏所带来的影响[10]。φ19和φ85分别代表PRR(19)–GR(37V19V) 所组成的坐标系和PRR(85)–GR(37V19V)组成的坐标中100%海冰组成的直线与GR坐标轴之间的夹角。根据文献[10],φ19和φ85设置如表1所示。

表1 南极角度值Table 1.Angles in Antarctic

NT2算法是通过搜索模拟样本建立的数据库,匹配最佳密集度数值,算法自身的特点导致数据结果的精度依赖于样本数据库的精度,而随着全球气候环境的变化,样本数据库的误差会逐年变化,精度也会受到影响。

2.3 ASI

ASI算法通过计算 89 GHz亮温数据的极化差异P,得到海冰密集度,算法方便高效。具体公式如式(7)所示:

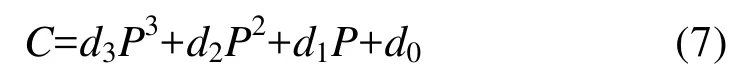
式(7)中的P为89H与89V高频数据之间的极化差异,系数d0、d1、d2、d3可通过求解式(8)得到:

式(8)中P0代表89 GHz的亮温极化差异在开阔水域的数值,P1代表89 GHz的亮温极化差异在100%海冰密集度区域的数值。ASI算法计算简便,所用到的原始数据仅为89 GHz的垂直极化与水平极化亮温数据。

2.4 基于改进FCLS的海冰密集度估算方法

本研究将NT2算法所使用的PRR(19)、PRR(89)和ΔGR三个参数引入基于FCLS的海冰密集度估算方法中,以获取高空间分辨率海冰密集度结果的同时得到多类型的海冰密集度数据。可将式(2)改写为式(9):

其中,T是t行1列的向量,t代表通道数;N=[TBW,TBFY,TBMY],分别代表不同地物类型的参考亮温;β=[CW,CFY,CMY],分别代表开阔水域、一年冰、多年冰所占比例。结合原始频段亮温数据求解海冰密集度可获得更高精度的海冰密集度结果[13],因此本研究不仅利用PRR(19)、PRR(89)、ΔGR三个参数建立海冰密集度求解方程,还结合19H、19V、37V、89H、89V五个通道。根据文献[13]和文献[16],求解过程中使用的参考亮温如表2所示。

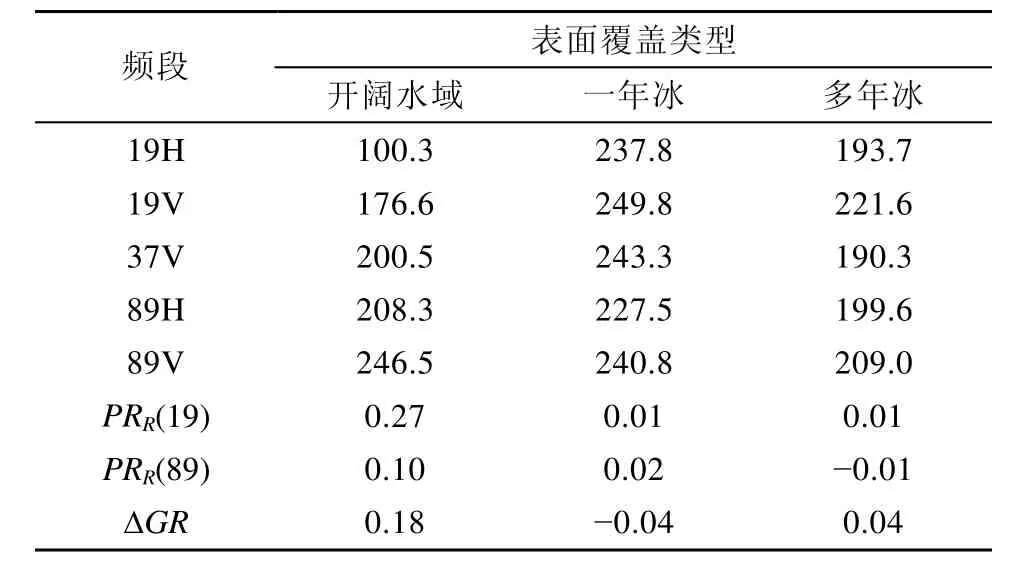
表2 各频段参考亮温Table 2.Reference brightness temperature of each frequency

相比低频数据,高频数据对大气情况更为敏感。为减少水汽对海冰密集度估算结果的影响,基于高频数据的海冰密集度估算方法通常引入大气不透明度参数[12]或使用天气滤波器以消除水气的影响。本文采用引入天气滤波器GR(37/17)和GR(23/19),分别去除云中液态水和水面上水蒸气的影响,计算公式为式(10)和式(11)[17]:

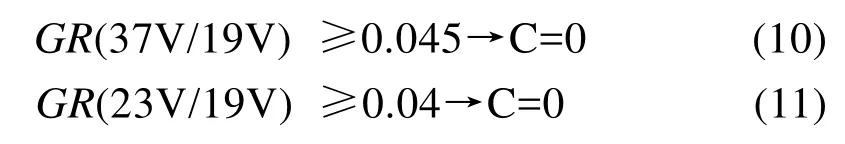
其中,C代表海冰密集度,当GR值大于设定的阈值时,将海冰密集度设为零。

3 精度验证

3.1 多种算法精度比较

利用改进的方法、NT2和 ASI算法,基于2002—2005年间的AMSR-E数据,完成南极地区海冰密集度的估算。并选取813个ASPeCt船测数据为实测海冰密集度数据对3种算法的精度进行验证,结果如表3所示。

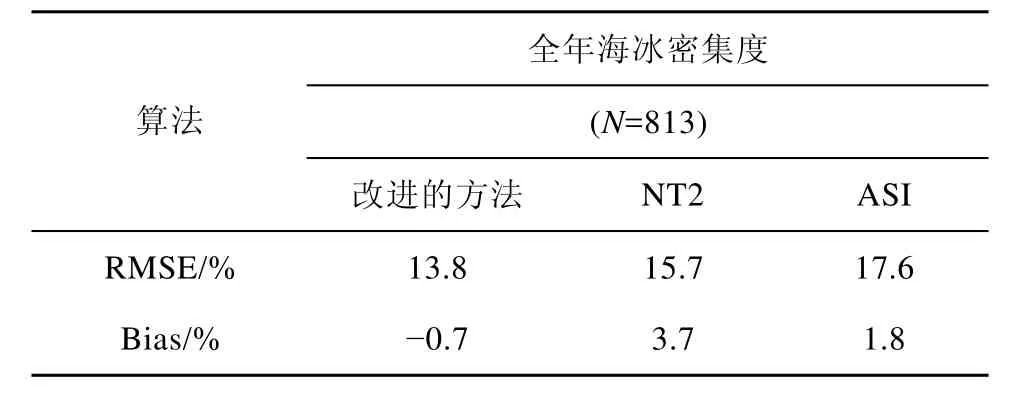
表3 改进的基于FCLS的海冰密集度估算方法、NT2、ASI全年估算精度Table 3.Accuracies of the improved FCLS、NT2 and ASI throughout the year

根据表3,从全年 RMSE分析,改进的方法获得更高的全年海冰密集度估算精度,NT2精度次之,ASI估算精度最低,改进的方法Bias也是3种算法中最小的。导致这3种方法精度差异的原因主要分为两点: 第一,改进的方法与 NT2不仅使用高频的89 GHz极化数据,还包括19 GHz的双极化数据以及 37 GHz的垂直极化数据,其中19 GHz的垂直极化数据在区分开阔水域与海冰时具有良好的特性,而ASI算法仅使用了89 GHz高频数据,因此改进的方法和NT2算法估算精度优于 ASI算法; 第二,改进的方法与 NT2相比,优点是不受模型误差的影响; 计算结果的非负性以及不同地物所占比例和为一的特点,一定程度上优化了结果的精度,使得改进的方法全年海冰密集度估算精度高于NT2。但计算所用到的原始数据决定了该算法对不同地表覆盖类型参考亮温的精度要求更高。

进一步的算法精度验证利用各月和各密集度的数据进行分析,结果如图2—图5所示。

根据图2a,从各月RMSE分析,整体趋势为先减小后增加,最小值出现在7月和8月,同时也是南极气温最低的时间; 根据图2b—d,3种算法各月RMSE最大值均分布于罗斯冰架和芬布尔冰架附近。

出现这种趋势的原因为气温影响着海冰表面状态,气温的升高导致海冰表面融化现象严重,进而导致表面极化差异与开阔水域的极化差异相近,部分海冰被误判为开阔水域; 气温的下降使海冰表面状态稳定,融化现象极为少见。改进的方法在 7月份精度较差,这主要是由两方面原因组成。首先7月份数据是在威德尔海观测得到,海面温度可能与改进的方法预先设定的参考温度相差较大; 其次由于 7月份实测数据有限,导致误差随机性增大。除去季节原因,位于罗斯冰架和芬布尔冰架的数据RMSE偏大,这主要由于冰架附近海水盐度较大,海冰温度偏低,实际亮温与参考亮温差距大,引起较大误差。

根据图3a,从各月Bias分析,3种算法均存在高估海冰密集度的现象。根据图3b—d,除罗斯冰架和芬布尔冰架区域以外,在威德尔海区域也得到了较大的Bias。

出现算法高估海冰密集度的现象,主要是由于南极大陆的低温高压与海面的低压形成强烈对比,风速快,增大了水面的粗糙程度,使其具有了海冰的极化特征,造成部分水域被误判为海冰。除去季节原因,在威德尔海得到了较大的Bias,这是由于该区域存在强劲的东风和旋回的北风[18],在两者共同作用下推动海冰移动,从而造成ASPeCt船测数据与AMSR-E数据在同一天内不同时段所得结果差异较大。

根据图4,分析各密集度RMSE,整体趋势为先增加后减小,最大值出现在海冰密集度60%处。

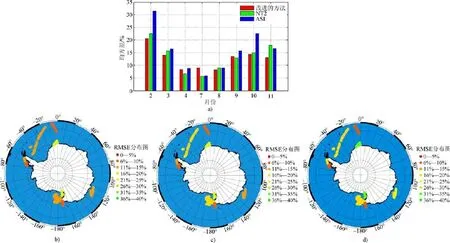
图2 改进的基于FCLS的海冰密集度估算方法、NT2、ASI各月均方差统计图.a)3种算法对比图; b)改进的方法; c)NT2;d)ASIFig.2.Statistics of RMSE with improved FCLS,NT2 and ASI in each month.a)comparison of three algorithms; b)improved FCLS; c)NT2; d)ASI

图3 改进的基于FCLS的海冰密集度估算方法、NT2、ASI各月偏差统计图.a)3种算法对比图; b)改进的方法; c)NT2;d)ASIFig.3.Statistics of bias with improved FCLS,NT2 and ASI in each month.a)comparison of three algorithms; b) improved FCLS; c)NT2; d)ASI

出现RMSE随海冰密集度先增加后减小这种趋势的原因为地表覆盖类型单一,参考亮温更接近于预设的数值,算法精度高。改进的方法在密集度最低和最高时精度并不是特别好,这是由算法本身特点决定的。改进的方法是基于最小二乘原理计算海冰密集度数据,在密集度最低和最高时,混合像元的概念被弱化,使用最小二乘求解的优势不明显。

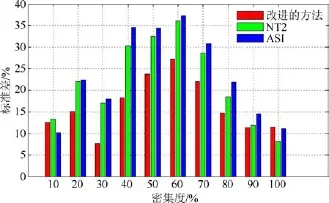
图4 改进的基于FCLS的海冰密集度估算方法、NT2、ASI各密集度均方差统计图Fig.4.Statistics of RMSE with improved FCLS,NT2 and ASI in each concentration

根据图5,从各密集度 Bias分析,三种算法最大值依然出现在海冰密集度60%处。

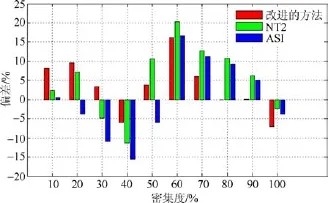
图5 改进的基于FCLS的海冰密集度估算方法、NT2、ASI各密集度偏差统计图Fig.5.Statistics of bias with improved FCLS、NT2 and ASI in each concentration

这表明在海冰与开阔水域所占比例大致相当时,3种算法精度所受到得影响最大。出现这种现象的原因是由混合像元的参考亮温与单一地表覆盖类型参考亮温差异所引起的。

3.2 不同类型海冰密集度结果精度比较

根据表4,从全年 RMSE分析,多年冰的RMSE比一年冰低2%; 全年一年冰Bias为−2.8%,小于零,多年冰Bias为2.2%,大于零。无论是从均方差还是偏差来看,改进的方法对多年冰密集度的估算精度都高于一年冰。

表4 改进的基于 FCLS的海冰密集度估算方法估算一年冰、多年冰的精度Table 4.Accuracies of the improved FCLS algorithm in first-year ice and multi-year ice

根据图6a,从各月RMSE分析,除11月以外,其余各月多年冰RMSE均小于一年冰,其中7月、9月和10月未观测到多年冰,所以RMSE为零; 根据图7a,从各月Bias分析,11月两者绝对值相差5.9%,2月、3月和4月误差相近,其余各月均表现为多年冰精度更高; 根据图6b、c和图7b、c,一年冰各月RMSE和各月Bias最大值均分布在罗斯海区域,多年冰各月 RMSE最大值分布在威德尔海区域,各月Bias最大值分布在罗斯海区域。

通过RMSE与Bias各月时序图综合分析发现,多年冰在 11月的精度不是很好,这主要由于 11月南极处于夏季,温度上升引起多年冰表面融化,冰厚减小,被误判为一年冰。海冰估算精度误差较大点主要分布在罗斯海和威德尔海区域,主要由于两片海域风力强劲,海面上的风造成海冰移动,同时增大了海面的粗糙程度。

根据图8,从各密集度 RMSE分析,除 90%的数据以外,多年冰 RMSE均小于一年冰; 根据图9,从各密集度Bias分析,密集度在40%、70%和80%情况下,一年冰Bias较小,其余情况均表现为多年冰精度更优。

出现一年冰Bias小于多年冰的主要原因是环境温度的变化导致多年冰精度下降; 其次,样本数量较少导致随机误差增大,也有可能导致这种现象。

以上数据综合表明改进的方法在估算多年冰的精度时优于一年冰,造成以上结果的原因主要是由多年冰本身的结构特点决定的。多年冰与一年冰相比结构更为稳定,存在周期更长,受温度变化影响小,稳定的结构使多年冰在亮温数据上表现为稳定的极化差异; 相比多年冰,一年冰的寿命较短,海冰表面容易因温度的短时间回升而出现大量的雪水,使其在亮温数据上表现出与开阔水域接近的极化差异。

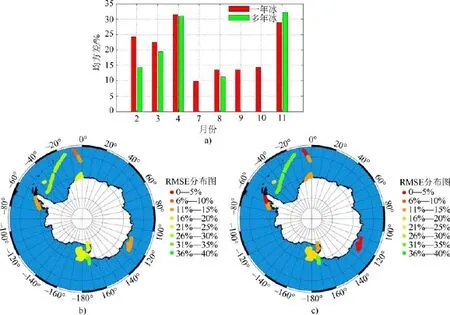
图6 基于改进的FCLS海冰密集度估算方法估算一年冰、多年冰的各月均方差统计图.a)一年冰与多年冰对比图; b)一年冰; c)多年冰Fig.6.Statistics of RMSE with improved FCLS about first-year ice and multi-year ice in each month.a)comparison between first-year ice and multi-year ice; b)first-year ice; c)multi-year ice

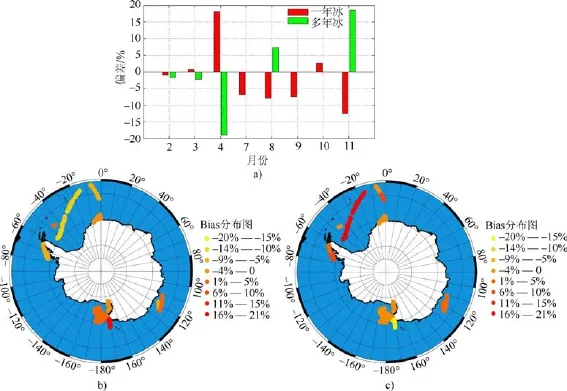
图7 基于改进的FCLS海冰密集度估算方法估算一年冰、多年冰的各月偏差统计图.a)一年冰与多年冰对比图; b)一年冰; c)多年冰Fig.7.Statistics of Bias with improved FCLS about first-year ice and multi-year ice in each month.a)comparison between first-year ice and multi-year ice; b)first-year ice; c)multi-year ice

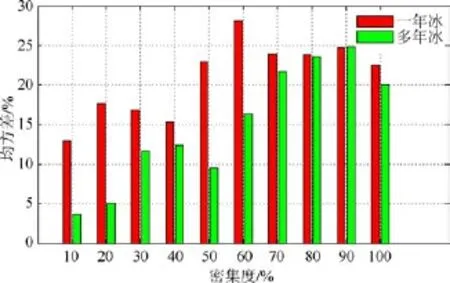
图8 基于改进的 FCLS海冰密集度估算方法估算一年冰、多年冰的各密集度均方差统计图Fig.8.Statistics of RMSE with improved FCLS about first-year ice and multi-year ice in each concentration

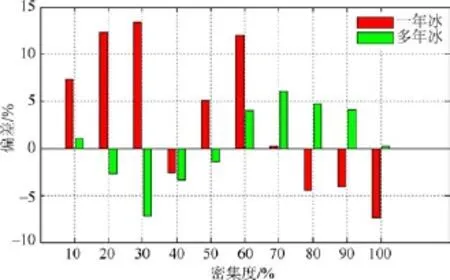
图9 基于改进的 FCLS海冰密集度估算方法估算一年冰、多年冰的各密集度偏差统计图Fig.9.Statistics of Bias with improved FCLS about firstyear ice and multi-year ice in each concentration

4 结论

本文将亮温极化梯度率和光谱梯度率引入基于FCLS的海冰密集度估算方法,以ASPeCt船测数据为实测海冰密集度数据,通过对比分析改进的方法、NT2算法和ASI算法获得的海冰密集度结果得出以下结论。

1.通过与ASI、NT2算法获得的海冰密集度结果比较,改进的方法在全年海冰密集度估算精度最优,RMSE和Bias分别为13.8%和−0.7%; 通过各月RMSE时序图可以看出3种算法均受到气温的影响,并呈现负相关。在7月、8月正值南极的冬季,气温达到最低,精度最高; 通过各密集度RMSE及Bias时序图可以看出3种算法均受到海冰密集度的影响,当密集度达到 51%—60%时,精度受影响最大。

2.在一年冰与多年冰的密集度估算精度中,改进的方法表现出了良好的特性。全年海冰密集度估算中,一年冰和多年冰RMSE分别为22.7%和20.7%,Bias分别为−2.8%和2.2%; 通过各月以及各密集度数据分析,与一年冰密集度估算相比,改进的方法对多年冰密集度估算更加准确,这是由于多年冰相比一年冰结构更加稳定。

由此可知,改进的方法在获得高分辨率多类型海冰密集度结果的同时,也得到了更优的精度,解决了基于高频数据的海冰密集度估算方法无法获得多类型海冰密集度数据和数据精度依赖模型的问题。改进的方法也存在着一些不确定性,如高频数据对大气情况更加敏感,大气中的水汽直接影响算法结果的精度; 混合像元内不同类型地物之间相互影响,导致一年冰、多年冰和开阔水域参考亮温的变化,对计算结果也会产生误差。

由于 FCLS算法本身的特点,改进的方法在处理误差的过程中也存在着一定的不足之处,后续研究考虑将算法公式中的误差系数n分离出有统计特性的项,通过物理模型或统计模型来改进;同时考虑到全球气候环境的不断变换,以及混合像元所引起的地表覆盖类型亮温值的不同,在条件允许的情况下,应尽可能实地测量数据获取符合研究区域时间区间的参考亮温。

此外,由于ASPeCt船测数据的时间、空间分布不同,不同类型海冰统计样本不一样,在一定程度上影响精度验证结果。下一步会搜集更多海冰密集度的实测数据,如高分辨率的极区影像数据,对结果进行验证,以此提高精度验证结果。

1 刘婷婷,刘一君,王泽民,等.基于多源遥感数据的北极新冰提取及范围时序变化分析[J].武汉大学学报(信息科学版),2015,40(11): 1473—1478.

2 Fraser A D,Massom R A,Michael K J.Generation of high-resolution East Antarctic landfast sea-ice maps from cloud-free MODIS satellite composite imagery[J].Remote Sensing of Environment,2010,114(12): 2888—2896.

3 Heinrichs J F,Cavalieri D J,Markus T.Assessment of the AMSR-E sea ice-concentration product at the ice edge using RADARSAT-1 and MODIS imagery[J].IEEE Transactions on Geoscience and Remote Sensing,2006,44(11): 3070—3080.

4 Wang L,Scott K A,Clausi D A.improved sea ice concentration estimation through fusing classified SAR imagery and AMSR-E data[J].Canadian Journal of Remote Sensing,2016,42(1): 41—52.

5 Tanaka Y,Tateyama K,Kameda T,et al.Estimation of melt pond fraction over high-concentration Arctic sea ice using AMSR-E passive microwave data[J].Journal of Geophysical Research: Oceans,2016,121(9): 7056—7072.

6 Ivanova N,Johannessen O M,Pedersen L T,et al.Retrieval of arctic sea ice parameters by satellite passive microwave sensors: a comparison of eleven sea ice concentration algorithms[J].IEEE Transactions on Geoscience and Remote Sensing,2014,52(11): 7233—7246.

7 Svendsen E,Kloster K,Farrelly B,et al.Norwegian remote sensing experiment: evaluation of the nimbus 7 scanning multichannel microwave radiometer for sea ice research[J].Journal of Geophysical Research,1983,88(C5): 2781—2791.

8 Andersen S,Tonboe R,Kern S,et al.Improved retrieval of sea ice total concentration from spaceborne passive microwave observations using numerical weather prediction model fields: an intercomparison of nine algorithms[J].Remote Sensing of Environment,2006,104(4): 374—392.

9 Cavalieri D J,Gloersen P,Campbell W J.Determination of sea ice parameters with the nimbus 7 SMMR[J].Journal of Geophysical Research: Atmospheres,1984,89(D4): 5355—5369.

10 Markus T,Cavalieri D J.An enhancement of the NASA team sea ice algorithm[J].IEEE Transactions on Geoscience and Remote Sensing,2000,38(3): 1387—1398.

11 Kaleschke L,Lüpkes C,Vihma T,et al.SSM/I sea ice remote sensing for mesoscale ocean-atmosphere interaction analysis[J].Canadian Journal of Remote Sensing,2001,27(5): 526—537.

12 Svendsen E,Matzler C,Grenfell T C.A model for retrieving total sea ice concentration from a spaceborne dual-polarized passive microwave instrument operating near 90 GHz[J].International Journal of Remote Sensing,1987,8(10): 1479—1487.

13 Liu T T,Liu Y X,Wang Z M.Fully constrained least squares for Antarctic sea ice concentration estimation utilizing passive microwave data[J].IEEE Geoscience and Remote Sensing Letters,2015,12(11): 2291—2295.

14 Worby A P,Comiso J C.Studies of the Antarctic sea ice edge and ice extent from satellite and ship observations[J].Remote Sensing of Environment,2004,92(1): 98—111.

15 Cavalieri D J,Markus T,Hall D K,et al.Assessment of AMSR-E antarctic winter sea-ice concentrations using aqua MODIS[J].IEEE Transactions on Geoscience and Remote Sensing,2010,48(9): 3331—3339.

16 王欢欢,Heygster G,韩树宗,等.应用AMSR-E 89 GHz遥感数据反演北极多年冰密集度[J].极地研究,2009,21(3): 186—196.

17 Yu Q L,Wang H,Wan L Y,et al.Retrieving the Antarctic sea-ice concentration based on AMSR-E 89 GHz data[J].Acta Oceanologica Sinica,2013,32(9): 38—43.

18 Venegas S A,Drinkwater M R.Sea ice,atmosphere and upper ocean variability in the Weddell Sea,Antarctica[J].Journal of Geophysical Research: Oceans,2001,106(C8): 16747—16765.