基于MF—DFA方法的外汇市场多重分形研究

王继田+李媛

摘要：文章采用MF-DFA方法研究汇率波动的分形特征，以说明人民币与美元汇率走势的长记忆性特征。并通过实证得出两个结论：一是人民币对美元汇率的波动严重依赖其前期波动， 前期汇率数值会全部传导到本期； 二是人民币汇率市场波动存在明显的分形维， 时间序列具有波动异方差性。

关键词：汇率波动；MF-DFA；多重分形

一、引言

汇率是各国进行贸易、资本跨国流动的前提，是连接各国经济往来的桥梁，因此汇率波动会对各国的经济产生一定的影响。汇率波动对经济波动及国际金融风险都具有良好的时效性和敏感性，研究汇率的波动特征能更好地把握汇率变化的规律，从而化解汇率波动对经济的冲击。反过来，经济的变化也会对汇率收益率波动造成冲击，影响汇率收益率的波动特征。

实证研究表明诸如外汇市场、股票市场、期货市场等并不是有效的，人民币对美元價格的变化并不是独立的，而是存在相关性，人民币对美元价格的变化并不服从正态分布，那么基于有效市场假说的经典金融市场理论存在着缺陷。Peters（1991）提出的分形市场假说（Fractal Market Hypothesis，FMH）提供了研究金融市场长时间序列的新方法和新思路，对市场特性的研究更为广泛、深入和切入本质。其中收益率的长记忆性引起很多学者和金融市场实际从业人员的广泛关注。认为人民币对美元波动的行为就像一个动力学系统，对一些外郁的冲击有快速和充分的初始反应，但是由于系统受长期稳定机制的控制，这个反应就会衰减，使其在短期内快速的消失。

基于分形理论的多重分形去趋势分析法（MF-DFA）能够有效去除局部趋势对时间序列标度的影响，可以探测不同时间标度下时间序列所呈现的分形特征，是研究非平稳时间序列长期幂律关系的有效手段。因此，本文拟采用MF-DFA方法研究人民币兑美元价格的波动。

二、研究方法

设时间序列x（t），t=1，2，…，N，其中N为时间序列的长度。

第一步：构造一列新的时间序列，

μ（t）=[x（i）-x] t=1，2，…，N。

第二步：将新的时间序列μ（t）分成Ns段，其中Ns=，并且记

μv（i）=μ（l+i） 1≤i≤s l=（v-1）s。

第三步：对数据μv（i）进行多项式拟合μv（i），得出残差εv（i）=μv（i）-μv（i） 1≤i≤s。

第四步：对每一个子序列进行去趋势处理，最终得到子序列降趋协方差公式。

第五步：定义q阶波动函数，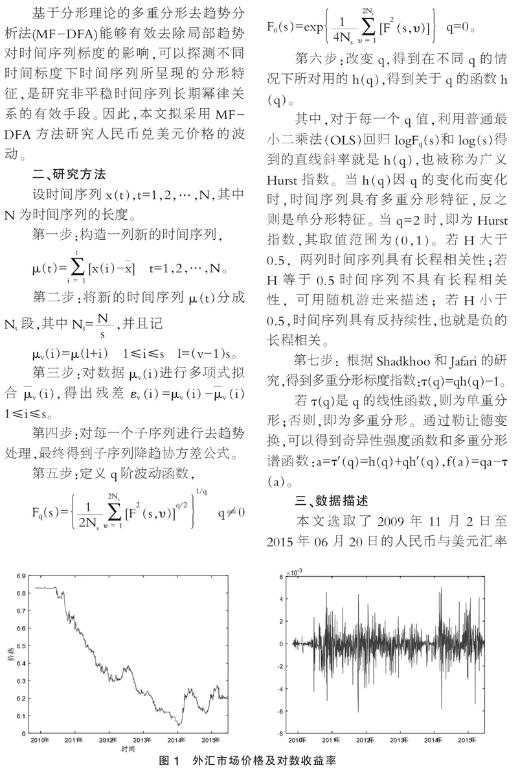

第六步：改变q，得到在不同q的情况下所对用的h（q），得到关于q的函数h（q）。

其中，对于每一个q值，利用普通最小二乘法（OLS）回归logFq（s）和log（s）得到的直线斜率就是h（q），也被称为广义Hurst指数。当h（q）因q的变化而变化时，时间序列具有多重分形特征，反之则是单分形特征。当q=2时，即为Hurst指数，其取值范围为（0，1）。若H大于0.5，两列时间序列具有长程相关性；若H等于0.5时间序列不具有长程相关性，可用随机游走来描述；若H小于0.5，时间序列具有反持续性，也就是负的长程相关。

第七步：根据Shadkhoo 和Jafari的研究，得到多重分形标度指数：τ（q）=qh（q）-1。

若τ（q）是q的线性函数，则为单重分形；否则，即为多重分形。通过勒让德变换，可以得到奇异性强度函数和多重分形谱函数：a=τ′（q）=h（q）+qh′（q），f（a）=qa-τ（a）。

三、数据描述

本文选取了2009年11月2日至2015年06月20日的人民币与美元汇率波动的数据1370条，数据的来源是wind数据库。将人民币与美元的价格进行对数化处理，得到日度对数收益率序列，Rett=ln（Pt+1/Pt）。人民币与美元的价格、对数收益率分别见图1所有时间序列的统计性描述如表1。

从图1中可以看出2009～2010年中期美元对人民币汇率一直保持在稳定的6.8左右，而2010年中期之后到2012年第一季度急剧下降到6.3，此后在2012年内有一个小幅度上升到6.4，到2014年缓慢下降到6.1以下。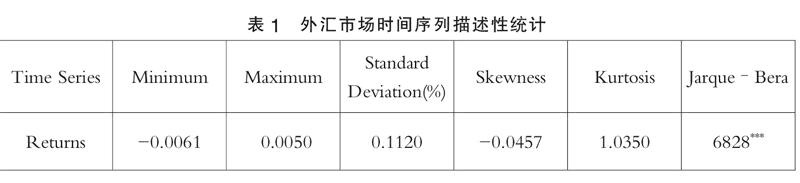

表1给出了外汇市场的基本统计性质。从中可以看出，总体来讲外汇市场比较稳定。时间序列的Jarque–Bera检验结果都在1%的显著性水平下拒绝原假设，说明外汇市场不符合有效市场假设下的正态分布假定。外汇市场的时间序列具有明显的尖峰厚尾分布特性，这与Jarque–Bera检验保持一致。最后由长记忆性检验可以看出，外汇市场的对数收益率呈现弱的反持续性，即通过长记忆性检验。

四、实证结果

前面的数据描述说明了外汇市场存在长记忆性特征，接下来采用前文介绍的MF-DFA方法定量估计时间序列的非线性相关关系和多重分形特征。通过公式画出了波动函数和标度的自然对数的散点图，并用普通最小二乘法拟合出所对应的直线，直线的斜率即为广义的Hurst指数（见图2）。从图2可以看出，随着线性标度q的增加，波动函数和标度之间存在着明显的幂率关系。

图3给出了外汇市场的广义Hurst指数与阶数之间的关系图。从之前的分析可以发现，如果广义Hurst指数都为常数，那么该时间序列就为单分形，否则，为多重分形。从图3中可以看出，对于原始时间序列，随着的q的增大，他们的hurst指数逐渐减小。外汇市场表现出了明显的多重分形特征。endprint

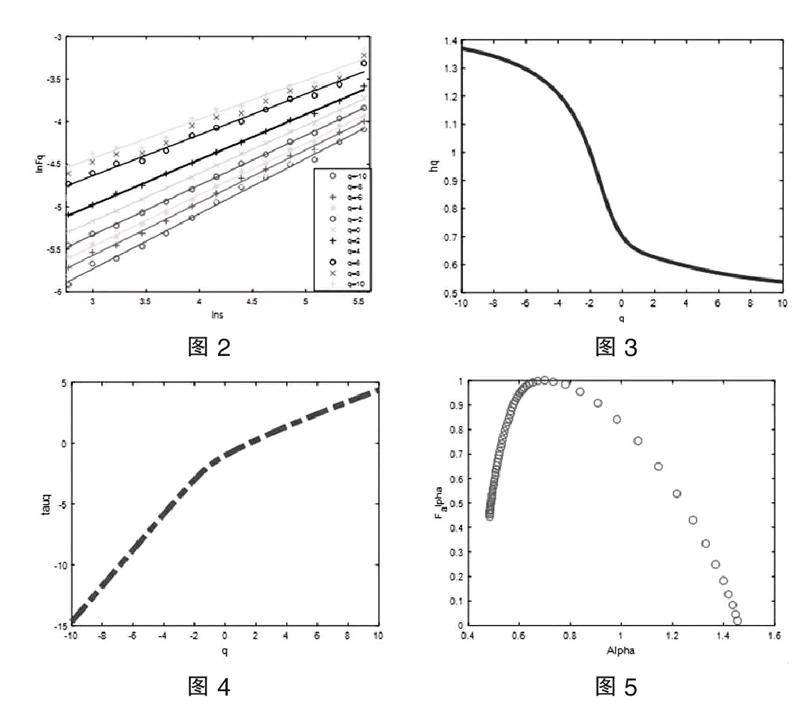
图4是外汇市场的标度指数图。从图4中可以看出外汇市场的自相关关系表现为递增凸函数，再次证明外汇市场具有多重分形特性。图5给出了外汇市场的多重分形谱图形。多重分形谱所刻画的是金融时间序列复杂的动力学机制，其宽度也被认为可以很好的估计多重分形强度，并反映市场的复杂程度。多重分形谱宽度越大，说明多重分形特征越强，进而可以得出长程相关性越大的结论，自然而然，市场的复杂程度也会越高。从图5中可以看出外汇市场序列分形谱呈现开口向下的类抛物线形状，分形谱宽度显著不为0，说明外汇市场序列存在明显的多重分形特征。

五、结论

本文通过对外汇市场多重分形分析发现，外汇市场存在着明显的长程自相关性，以此为基础，又进一步研究了它们之间的动态机理。得到了以下的结论。

1. 人民币对美元汇率的波动严重依赖其前期的波动， 前期汇率数值会全部传导到本期，外汇市场时间序列在统计上表现出明显的非正态性、尖峰厚尾和长期记忆性。

2. 采用MF-DFA方法进行研究发现，外汇市场存在明显的多重分形特征，通过对原始序列进行随机重排和概率分布替代发现，对于外汇市场，长期记忆性和厚尾分布都是其分形的重要来源。在外汇市场，信息不会完全公开，对于投资者而言，信息的获得以及对新信息的消化都不是立即的，这个时间的不确定性使投资者不能准确的把握市场。当新信息持续出现和历史信息的累计效应交互作用时，大量投资者可能会同时做出反应，造成市场大幅度波动。因此，优化市场投资结构，加强信息监管，减少内幕消息和交易，是外汇市场稳定发展的重中之重。

3. 从实际角度出发可以得到如下结论：人民币升值有利于我国商品进口；国外进口商品价格下降，可以增加我国人民对进口商品的需求，从而增加进口数量；有利于稳定国内物价和提高收入。

参考文献：

[1]黄健柏，程慧，郭尧琦，等.金属期货量价关系的多重分形特征研究——基于MF-DCCA方法[J].管理评论，2013（04）.

[2]Mandlebrot， B. B. The Fractal Geometry of Nature[M]. San Francisco： Freeman， 1982.

[3]H.E. Hurst，Long-term Storage Capacity of Reservoirs[J].Transactions of the American Society of Civil Engineers，1951（116）.

[4]H.E. Hurst， A Suggested Statistical Model Of Some Time Series Which Occur in Nature[J]. Nature， 1957.

[5]张永东，毕秋香.中国股票市场多标度行为的实证分析[J].2002（04）.

[6]何建敏，常松.中国股票市场多重分形游走及其预测[J].中国管理科学，2002（03）.

[7]苑莹，庄新田.中国股票市场的长记性与市场发展状态[J].数理统计与管理，2008（01）.

[8]胡雪明，宋学锋.深沪股票市场的多重分形分析[J].数量经济技术经济研究，2003（S）.

[9]施锡锉，艾克凤.股票市场风险的多重分形分析[J].统计研究，2004（09）.

[10]徐龙炳，陆蓉.R/S分析探索中国股票市场的非线性[J].预测，1999（02）.

（作者单位：广西师范大學经济管理学院）endprint