用“正比例”和“反比例”的意义去解答有关的实际问题

叶高社

（甘肃省西和县汉源镇北关小学）

学习了正、反比例的意义与判断后，其作用是什么呢？那就是在实际生活中的应用。我们知道，数学源于生活，而又服务于生活，只有将两者充分地结合在一起，才能体现出数学的价值。

学生学习了正、反比例的判断后，对其判断的方法已经熟记于心，但用此方法来解答实际的问题，又显得束手无策，将两者有效地结合起来，关键是找出“切入点”，这“切入点”就是“先判断，再连接”。在解答实际问题时，先要进行正确的判断，写出成正（或反）比例的关系式，如果是正比例关系，依据关系式，寻找两个比，再用等号连接；如果是反比例关系，就寻找两个积，再连接，特别注意的是所设的未知数一定要看成一个比例量去参与列比例式。

例如：（正比例）

一个晒盐场用100克海水可以晒9克盐，照这样计算，如果一个盐场一次投入585000吨海水，可以晒出多少吨盐？

解：设放入585000吨盐水可以晒出x吨盐

第一步：分析判断

海水的出盐率一定，海水的质量与所晒盐的质量成正比例。关系式是：盐的质量÷海水的质量=出盐率（一定）

第二步：寻找两个比例式

第一个比例式：9∶100 第二个比例式：x∶585000

第三步：连接

9∶100=x∶585000

解得：x=52650

答：略。

例如：（反比例）

学校的小商店有两种中性笔，小明带的钱刚好买4支单价是1.5元的，如果他想买单价是2元的中性笔，可以买几支？

解：设如果买单价是2元的中性笔，可买x支。

第一步：分析判断

单价：1.5元 数量：4支

2元 x支关系式：数量×单价=总价（一定）。因为总价（一定），所以数量和单价成反比量。

第二步：寻找两个积。

1.5×4 2×x

第三步：连结

1.5×4=2×x

解得：x=3

答：略

解这类实际问题，一定要写出正确的关系式，才能列出正确的比例式，如果判断错误，这道题是解不对的。

以上所讲的两例，只是我们遇到的最简单的问题，而在我们的实际生活中还会出现比较复杂的问题，就需要我们仔细分析，寻找最佳的解题方法。一般情况下，用正、反比例解答实际问题，有直接和间接两种解题方法。所谓直接解题方法就是“问什么设什么”了，即：需要求的问题，我们直接设为x表示，然后列式求解，所谓间接解法就是“问什么不设什么”，需要“什么”而“去设什么”，即题目中要解决的问题，我们不把它设成x，而在列比例的过程中，需要哪一个量，就把它设为x。（设未知数的目的就是把未知量变成已知量）

例如：一堆煤如果每天烧0.3吨，30天烧完，如果每天节约0.1吨，可以比计划多烧多少天？

分析：每天的烧煤量×烧煤的天数=一堆煤的总吨数（一定）

用间接解法，我们如果求出实际烧煤的天数，就可以求出多烧的天数。解：设每天节约0.1吨，实际可以烧x天，列表如下

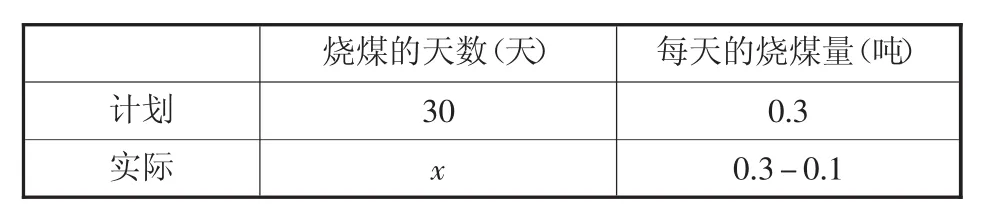
烧煤的天数（天） 每天的烧煤量（吨）计划 30 0.3实际 x 0.3-0.1

因为积一定，所以列式为：

30×0.3=x×（0.3-0.1）

解得：x＝45

45-30＝15（天）

答：略

直接解法：就是把要求的问题直接设为x

解：设如果每天节约0.1吨，实际比计划多烧x天。列表如下

烧煤的天数（天） 每天的烧煤量（吨）计划 30 0.3实际 30＋x 0.3-0.1

列式为：30×0.3=（30＋x）×（0.3-0.1）

解得：x＝15

答：略

间接解法与直接解法最大的区别就是：一个是直接计算的结果就是所求的答案，另一个是计算的结果不是我们最后要解决的问题，还需要进行最后一步的计算，才能求解。这两种方法各有利弊，直接解法设未知量时很容易，但列比例式比较困难，而间接解法把所需的量设为未知数比较困难（即所需量的寻找是解题的关键），而列比例式时就很容易。因此在教学的过程中，我们可以把这两种方法有效地结合起来，但一定注意，不要设未知数时用直接解法而列比例式时用的又是间接解法，设者与解者相互矛盾。