区域负荷趋势特征分析与金字塔模型超短期预测方法

许 刚,吴舜裕

(华北电力大学 电气与电子工程学院,北京 102206)

0 概述

区域负荷指配电网中以馈线分段开关或联络开关围成的小范围用电区域[1]。区别于传统电网负荷特征,区域电网内的负荷受时间、地区、用电性质、气候以及突发性事件等客观因素的影响较大[2],易形成多个趋势拐点降低预测精度,从而进一步影响ADN控制策略的精确性。因此,区域负荷超短期预测对实施有效的配网运行控制具有较为显著的影响,是主动配电网实时协同运行控制以及自愈控制的关键技术之一[3]。

现有的超短期负荷预测方法主要可分为线性外推、支持向量机、神经网络以及大数据挖掘等[4]。文献[5]应用灰色模型纵向预测和横向趋势外推修正的方法,对负荷最新发展趋势进行更新,实现超短期负荷预测。文献[6]采用模糊加权最小二乘向量机法,并考虑预测点与历史负荷数据之间的影响关系,根据“近大远小”原则,提出了超短期负荷预测方法。文献[7]在短期负荷预测的基础上,考虑突发事件、日期类型等因素,提出超短期预测方法,较好地解决了负荷拐点的预测精度问题。文献[8]为解决最小二乘支持向量机(Least Squares Support Vector Machine,LSSVM)参数对预测精度的影响以及单一模型预测误差高的问题,提出了由集合经验模态分解(Ensemble Empirical Mode Decomposition,EEMD)与LSSVM组成的预测模型,并通过贝叶斯推理确定模型参数,实现了家庭负荷的超短期负荷预测。文献[9-10]分别采用RBF与小波神经网络建立了负荷预测模型。文献[11]运用大数据技术,提出基于随机森林算法的并行负荷预测方法,并通过将负荷影响因素分析与预测并行化处理,提升预测模型大数据处理与计算能力。然而,由于区域负荷水平较低,人员构成相对简单,其对部分外界因素(气象、时间、日期类型等)变化更为敏感,易出现负荷突升、突降等现象。现有研究成果在预测过程中对负荷变化特征实时跟随方面尚存在一定欠缺,对存在较为频繁的功率突升、突降以及多功率拐点的区域负荷预测不完全适用。

针对区域负荷在变化过程中易出现多个波峰、波谷以及趋势拐点等特征,为提升超短期预测精度与稳定性,本文提出金字塔结构自适应滚动淘汰机制下的区域负荷超短期预测策略。通过灰色关联分析提取与区域负荷趋势具有显著相关性的客观因素作为学习样本,加快算法计算速度。利用自适应增强随机权网络(Adaptive Boosting Random Weighted Network,Ada-RWN)对学习过程中的样本权重进行自适应调整,改变神经网络初始值分布,提高全局最优解逼近效率。同时,在预测过程中保留精度最高的若干模型作为备选集,滚动淘汰预测精度较低的预测模型,提升算法对区域负荷趋势变化特征的适应性,并保证负荷预测精度的稳定性。

1 区域负荷特征分析

相对于传统负荷,区域负荷供电范围较小,其功率水平对日期类型、环境因素等客观因素变化也更为敏感。同时,由于区域负荷受用户主观行为影响较大,负荷水平发展趋势会出现一定的发散性特征,即实时功率与历史功率之间的关联性较弱。此外,相对于传统负荷日功率曲线一般只受节假日类型影响,区域负荷一周7 d的负荷曲线也会呈现不同的变化特征。以下通过将区域负荷数据与比利时电力传输供应商Elia所提供的配网运行实时功率数据(15 min)进行对比,分析区域负荷在波动性、趋势惯性以及周负荷特征方面的差异。

1)波动性与惯性

负荷波动性指在一定时间周期内,负荷功率与对应周期内平均功率之间的偏离程度。具体在负荷变化过程中表现为,负荷曲线峰谷差以及波峰、波谷数量等特征。惯性指负荷水平变化过程中,其趋势的发散性特征。

以图1所示同一日区域负荷与Elia负荷数据为例,将负荷数据分别归一化后,对比区域负荷与传统负荷变化特征。

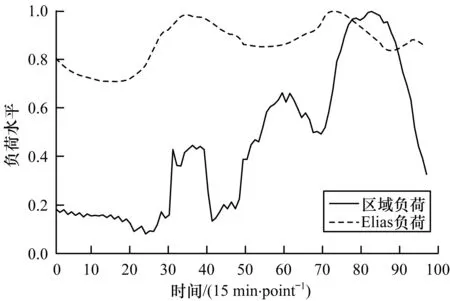
图1 日负荷曲线对比

如图1所示为区域负荷与配电网负荷数据经归一化后的变化趋势对比。区域负荷与普通配电网负荷在峰谷差、峰谷数量等方面存在较大差别。普通负荷的变化趋势通常较为平稳,负荷峰谷差大约只有30%左右。而区域日负荷具有多个明显的波峰、波谷,且峰谷差约为90%。同时,在负荷变化过程中,区域负荷在一定时间段内会出现多个极值,形成功率拐点,对负荷预测精度的稳定性造成较大影响。

相对波动性指标(Relative Volatility Index,RVI)用于分析数据序列的发散趋势。RVI指标越大,则代表对应负荷序列的相对波动性越强,其计算方法如式(1)所示。

(1)

其中,p1、pend、pmax、pmin分别为负荷序列中的首尾值以及最大负荷、最小负荷。

根据式(1)对图1的负荷曲线进行相对波动性计算可得,区域负荷与Elia负荷的RVI指标分别为0.157 1、0.135 1。由此可见,在区域负荷变化过程中,其负荷水平呈现更强的发散特征,即后一时段的负荷水平与历史负荷之间的关联性较弱。

2)周负荷特征

图2与图3为区域负荷与Elia负荷归一化后7 d样本数据。通过对比曲线对比特征可知,区域负荷一周内的负荷曲线虽然存在一定相似性,但每天的负荷水平、拐点、波动性等均存在较大差异。而Elia配电网的负荷曲线则明显形成工作日与周末2种负荷变化类型,且日期类型的负荷水平、变化趋势基本重合。因此,相对于传统负荷具有较为明显的日期类型关联特征,区域负荷在同类日期类型下,同样可能形成趋势各异的功率曲线,其负荷水平随着外界条件与工作日程的变化而形成多种变化模式,并形成多个负荷拐点,降低了负荷预测精度与稳定性。

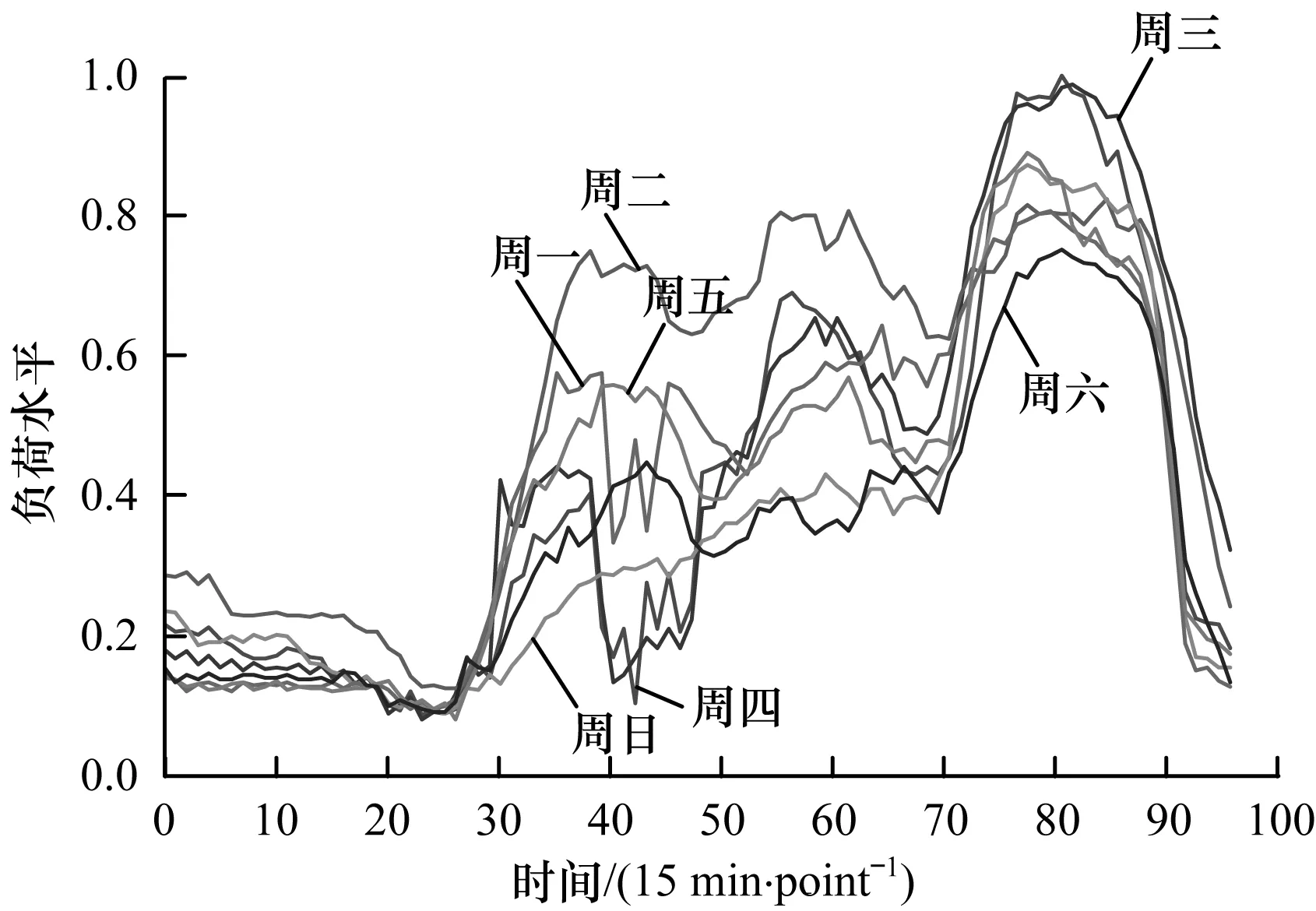
图2 区域周负荷曲线

图3 Elia周负荷曲线

2 超短期负荷预测模型

2.1 自适应增强随机权网络

与中短期负荷类似,超短期负荷同样受到天气、社会活动和节假日等因素的影响,在时间序列上表现为非平稳的随机过程,但是影响系统负荷的各因素中大部分具有规律性,与负荷数据有较强的关联特性,从而为实现有效数据的提取提供了可能[12-13]。因此,为提升预测模型训练速度,采用灰色关联分析区域负荷数据与气象数据之间的关联性,提取负荷敏感因素[14-15]。

采用图4所示随机择取网络结构内权权重的方法提升计算速度[16-17]。

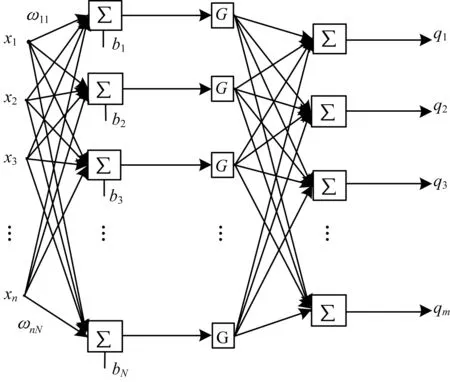
图4 单隐层前馈神经网络结构

(2)

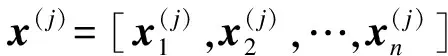
Hβ=T

(3)

(4)

即:

(5)

其中,‖·‖F表示矩阵的Frobenius范数。

由此,可得方程组的最小二乘解:

(6)

由于区域负荷变化趋势惯性较低,为更好识别预测日负荷趋势变化模式,将若干局部样本学习的随机权网络模型合并为全样本加强学习的集成模式,即自适应增强随机权网络模型(Ada-RWN)。通过自适应调整学习过程中的样本权重值,合并多个初值不同的随机权网络,提升全部最优值的求解效率。

(7)

随机权网络fiter的样本训练误差为:

(8)

由err的大小实现对训练样本权重的自适应性更新,有:

(9)

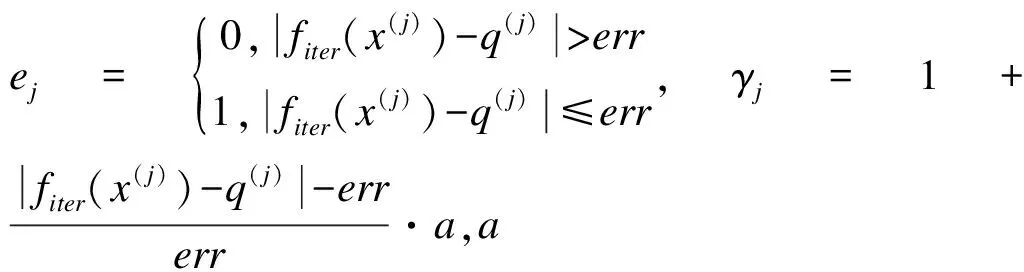
(10)

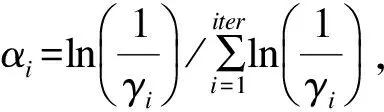
2.2 金字塔滚动淘汰机制

区域负荷趋势在发展过程中由于受客观条件的影响较大,使得其趋势惯性较弱。例如在办公区域中,工作日程或天气突变均可能导致后续负荷趋势变化模式与历史变化模式不同。针对该变化特征,构建图5所示金字塔结构负荷预测模型滚动淘汰机制,实现对负荷变化模式的自适应调整,提升预测精度及其稳定性。

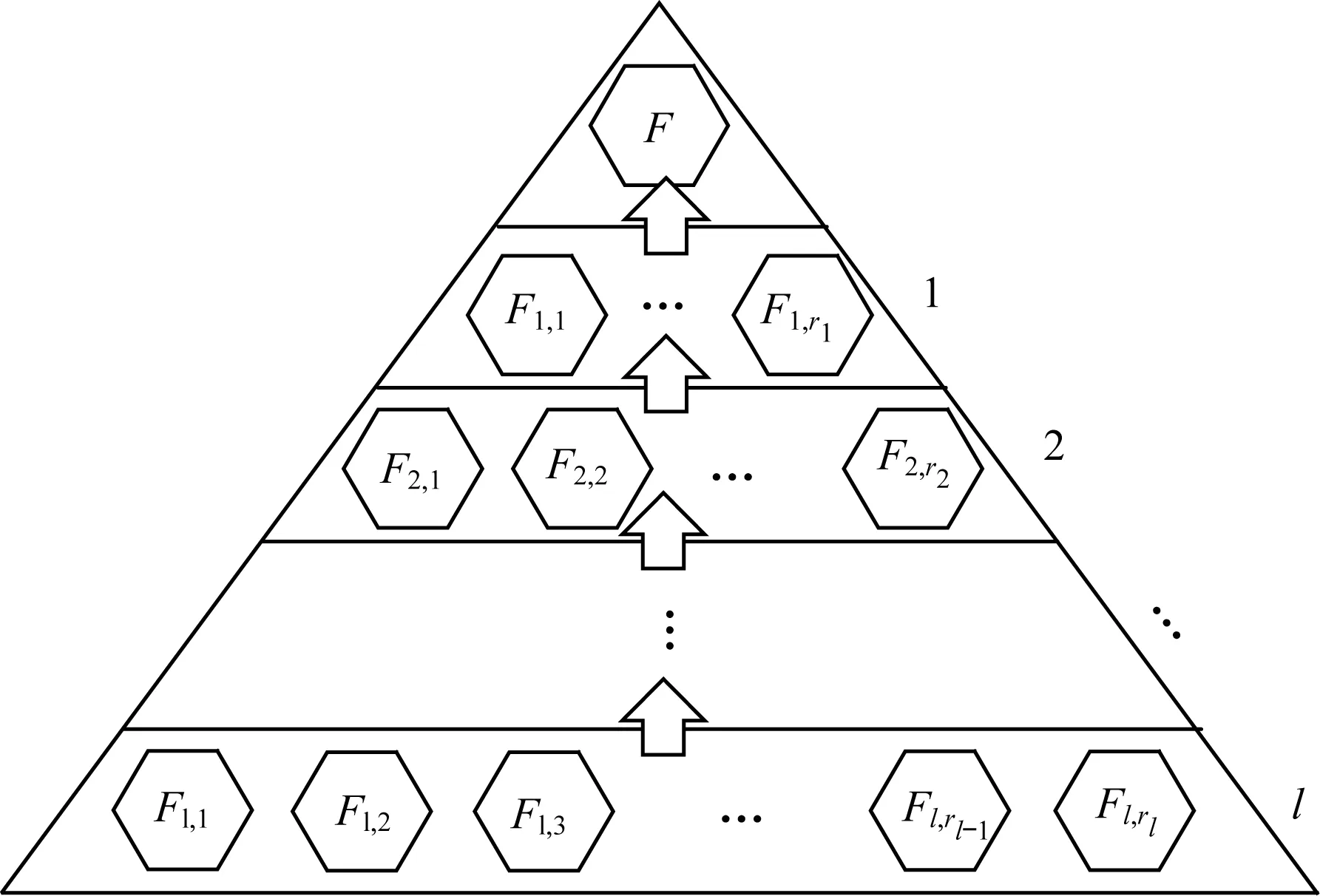
图5 金字塔滚动淘汰机制示意图

如图5所示,负荷超短期预测滚动淘汰机制由顶层预测模型F与l层备选预测模型构成。其中,备选模型层中预测模型个数为rl,且rl≥rl-1。为保证所采用预测模型的精度稳定性,所构建金字塔采用自下而上逐层竞选的模式。在负荷预测过程中,当下层预测模型连续δ个预测点精度高于上一层某个预测模型时,则2个模型的所属层次进行互换。同时,引入末尾淘汰机制保证金字塔中预测模型的更新率。

图6所示为滚动淘汰机制下的区域负荷超短期预测流程,所提超短期负荷预测流程分为3个部分:模型训练,预测精度统计与对比,金字塔滚动淘汰。其中,金字塔滚动淘汰又可分为:1)末尾淘汰;2)顶层替换;3)层间更新。设预测精度统计周期为δ,以t至t+δ时滚动淘汰过程为例,分别论述滚动淘汰3个部分的实行机制。

如图6所示,顶层替换与层间更新均经过各自更新判定与模型选择2个环节。以层间更新为例,其运作过程分为2个过程:1)判断是否进行模型更新,形成逻辑判断结果Y3与N3;2)根据Y3与N3,进行层间更新->金字塔更新选择器。在金字塔更新过程中,若判断某一层的预测模型精度低于下层模型,则将对应的2个模型进行所属层次调换,并形成逻辑条件Y3。此时,对应的选择器开关也切换至Y3侧,并输出相应的变化结果至金字塔模型,形成更新后的金字塔模型。

金字塔滚动淘汰过程中各环节具体运作机制与判定原则如下所述:

1)末尾淘汰

t时刻,根据模型训练流程形成新的自适应增强随机权网络预测模型Ft。t+δ时刻,将模型Ft与第3层中备用预测模型在δ时间段内的预测精度进行对比,若存在一个备用模型Fn3的预测精度统计值小于模型Ft的精度,则删除使用Ft替换Fn3;否则,删除模型Ft。

2)顶层替换

设实际负荷预测值有模型F输出。与末尾淘汰的机制相似,若存在金字塔备用模型中第1层的预测模型Fn1在周期δ内的预测精度统计值高于F,则模型F与模型Fn1互换所属层位置,即在t+1时刻采用模型Fn1进行负荷预测并输出结果。

3)层间更新

层间更新只发生在相邻备用层之间,即1、2层之间更新,2、3层之间更新。其更新机制与前文的末尾淘汰、顶层更新具有一定相似性,只有相邻层间模型的预测精度在统计周期δ内出现下层模型精度高于上层模型时,将对应的2个模型所述层级进行互换。限定只有相邻层间的模型才能进行层间更新的目的是为了保证只有预测精度稳定性最高的预测模型才能逐步提升其所属层级,并最终成为预测模型。

3 仿真分析

为验证所提自适应滚动淘汰机制下的区域负荷超短期预测精度及其稳定性,以某高校一年的负荷作为实验对象进行超短期负荷预测。所用数据采样间隔为5 min,一天共288个数据点。滚动淘汰过程中,为保证预测速度,设定淘汰周期为20 min,即δ=4。由于高校教学在工作日与双休日、节假日等休息日有较大变化,将日期类型设为工作日与休息日2类,即有W={1,2}。激活函数选用Sigmodal函数,即G(x)=1/(1+e-x)。在对历史数据的离线学习中,隐层神经元数量为N=15,权值调节步长为a=0.15,调节系数取λ=0.995,初始化样本集合的权重分布为全1分布,循环次数上限为200。在滚动淘汰过程中,为保证计算效率与预测精度的稳定性,设定第l层备用层的模型数量为2l个。在本文负荷预测过程中,为保证算法运行速度与预测精度,设定l=3。

以平均温度、最高温度、最低温度、气压、平均湿度、平均风速、雨量、辐射度这8个因素作为关联分析输入,计算各气象数据与负荷变化之间的关联性,得到图7所示的关联度分布。

图7所示为各气象因素与区域负荷变化趋势的关联系数分布,关联系数越趋近于1,则代表该气象因素对负荷变化的影响越大。其中,平均温度、最高温度、最低温度、平均湿度、平均风速这5个指标明显高于其他3个气象数据,因此取其作为预测模型的输入量,进行预测模型训练。

以某学校部分教学楼作为区域负荷预测实验样本数据,对该负荷一周的用电功率进行预测,得到图8所示的预测结果。

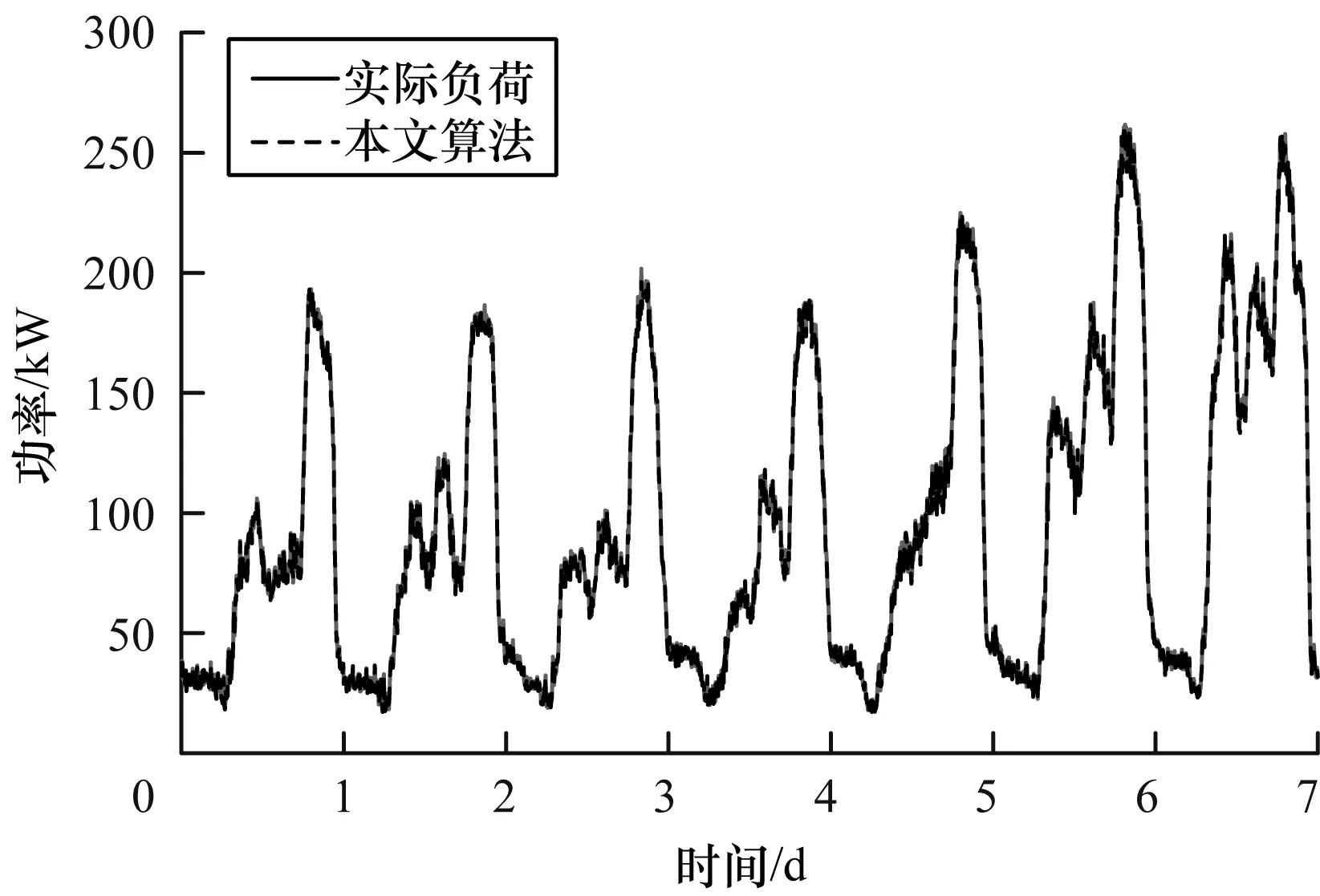
图8 一周区域负荷超短期预测结果

如图8所示,区域负荷由于其供电范围较小,在用电高峰期间出现多次功率突升与突降现象,具有多个明显的功率拐点。然而,在采用所提滚动淘汰机制进行区域负荷超短期预测后可较好地跟随负荷功率变化趋势,且未出现明显预测误差。预测结果显示所提算法具有较好的预测精度。

将周区域负荷数据作为实验对象,对比所提方法与改进灰色模型(IGM)[5]、自适应双向加权最小二乘支持向量机模型(ABW-LSSVM)[6]以及集合经验模态分解与最小二乘支持向量机组合预测模型(EEMD-LSSVM)[8]3种典型超短期预测方法,验证本文方法的有效性。

为衡量本文方法对预测精度的有益效果,采用预测值绝对平均百分比误差(MAPE)与均方根误差(RMSE)衡量预测精度。计算方法如式(11)、式(12)所示。

(11)

其中,x与x0指负荷预测值与真实值,k为预测样本负荷点个数。

(12)

其中,pfore、preal分别为区域负荷预测值与真实值序列。

对预测结果进行统计分析,得到表1所示不同预测模型下的性能对比。

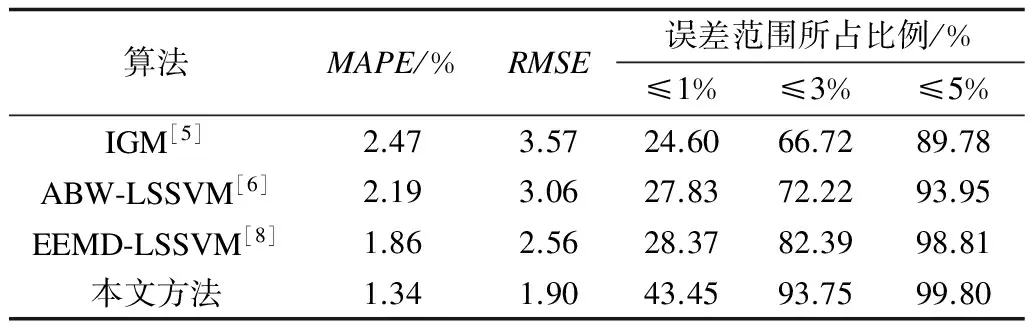
表1 区域周负荷超短期预测性能对比

由表1可知,所提区域负荷超短期预测方法的绝对平均百分比误差与均方根误差处于较低水平,具有较高的预测精度。

进一步分析周负荷超短期预测结果中同一时刻不同方法的误差分布情况,得到图9所示的误差分布情况。

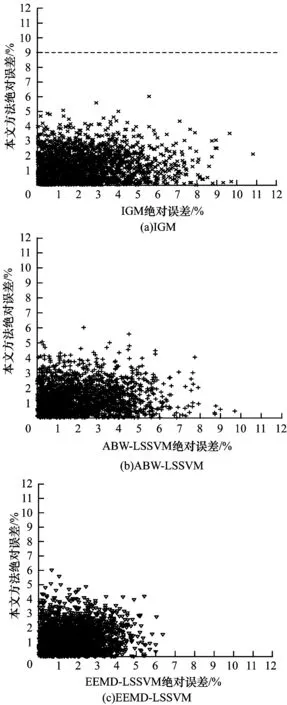
图9 负荷预测误差分布对比

图9所示为本文所提预测方法与其他文献3种方法预测绝对百分比误差的散点对比图,每一个散点对应一个时刻预测结果的绝对百分比误差。纵坐标为本文方法,横坐标分别为3种对比方法结果。由图9(a)、图9(b)可知,对应方法的预测误差分布更偏向于误差较高的方向。对比绝对百分比误差大于5%的预测点,IGM与ABW-LSSVM的分布密度明显较高。由图9(c)可知,虽然本文方法的最大误差略大于EEMD-LSSVM方法(均处于5%附近)。但误差处于3%～4%、4%～5%区间的点,EEMS-LSSVM的分布密度均大于本文方法。由此可见,虽然本文方法预测结果存在部分时刻的预测精度不高,可总体来说,本文方法预测误差较低点的分布密度均高于对比方法,平均预测误差也低于对比方法。为进一步验证算法预测精度的稳定性,计算不同方法的绝对百分比误差的均方差值来表示不同误差的离散程度,以得到区域负荷水平变化频繁情况下算法预测精度的稳定性。IGM、ABW-LSSVM、EEMD-LSSVM以及本文方法绝对百分比误差的均方差分别为1.84、1.62、1.19、0.97。

以预测精度最高的EEMD-LSSVM方法与本文所提方法预测结果作为对比,对比金字塔淘汰预测的过程及其优势。由于在用电低谷部分负荷波动较低,各方法预测精度均较好。因此,以部分用电高峰期8∶00—17∶00的预测结果作为实验对比,如图10所示。

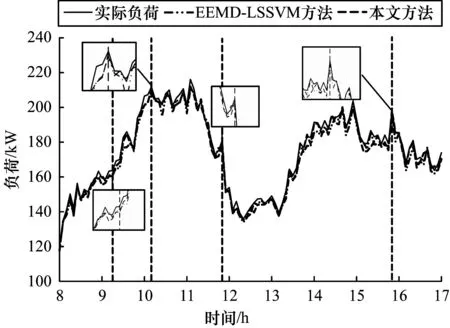
图10 用电高峰期模型滚动淘汰示例

图10所示为EEMD-LSSVM方法与本文方法预测曲线的对比,引线所指为金字塔进行顶层模型替换的预测点。模型替换的原则为当发现现有预测模型最近3个预测点的预测精度平均值小于下层模型,则进行模型替换动作。如图10所示,在预测过程中,金字塔结构总共进行了4次顶层模型替换动作。以第2次模型替换动作为例,在模型替换前,由于区域负荷变化趋势出现突变,预测模型的精度出现连续下降现象。此时金字塔模型中下层预测模型的预测统计精度高于当时正在使用的预测模型。因此,进行了顶层模型替换工作。顶层模型替换后,预测精度得到了明显的改善。对比同时段EEMD-LSSVM方法,该模型由于无法及时适应区域负荷变化特征,在后续时刻出现了较大的预测精度不稳定现象。由此可证明,本文方法可有效提升模型对区域负荷变化趋势突变的适应性,提高预测精度稳定性。

通过上述论述可知,本文方法的优势主要体现在:1)对区域负荷的预测精度较高,即MAPE较小;2)预测误差较为稳定,不会出现较大波动,即误差离散度(均方差)较小;3)对于负荷变化拐点附近的精度较高,可有效降低负荷趋势突变对预测精度的影响。

4 结束语

为抑制区域负荷弱趋势性对负荷预测精度的影响,本文提出了自适应滚动淘汰机制下的超短期负荷预测方法。通过灰色关联分析提取与区域负荷关联特征较大的客观因素,提高模型运算速度。然后利用样本权重自适应调整,实现对区域负荷变化趋势与拐点的有效把握。在此基础上进一步加入滚动淘汰机制,采用预测模型定期更新淘汰的方法,降低区域负荷特征变化对预测精度的影响,增强超短期预测精度的稳定性。本文方法可为主动配电网区域能量优化、运行管理策略等提供良好的数据支撑作用,提升区域电网运行的经济性与稳定性。

[1] 刘 健,勾新鹏,徐精求,等.基于区域负荷的配电网超短期负荷预测[J].电力系统自动化,2003,27(19):34-37.

[2] 甘 雯.小负荷大波动地区短期负荷预测模型研究[D].杭州:浙江大学,2007.

[3] 王娟娟,王宏安.基于多智能体混合调度的电网自愈系统[J].计算机研究与发展,2017,54(4):720-730.

[4] 姚佳馨,田慧欣.基于改进数据驱动子空间算法的电力负荷预测[J].计算机工程,2015,41(5):311-315.

[5] 张红旭,姚建刚,曹 伟,等.基于改进灰色模型的超短期负荷预测[J].电力系统及其自动化学报,2009,21(6):74-77.

[6] 王 岗,姜 杰,唐昆明,等.基于自适应双向加权最小二乘支持向量机的超短期负荷预测[J].电力系统保护与控制,2010,38(19):142-146.

[7] 路 轶,王民昆.基于短期负荷预测的超短期负荷预测曲线外推法[J].电力系统自动化,2006,30(16):102-104.

[8] 王 新,孟玲玲.基于EEMD-LSSVM的超短期负荷预测[J].电力系统保护与控制,2015,43(1):61-66.

[9] ZHANG Yun,QUAN Zhou,SUN Caixin,et al.RBF Neural Network and ANFIS-based Short-term Load Forecasting Approach in Real-time Price Environment[J].IEEE Transactions on Power Systems,2008,23(3):853-858.

[10] GUAN C,LUH P B,MICHEL L D,et al.Very Short-term Load Forecasting:Wavelet Neural Networks with Data Pre-filtering[J].IEEE Transactions on Power Systems,2013,28(1):30-41.

[11] 王德文,孙志伟.电力用户侧大数据分析与并行负荷预测[J].中国电机工程学报,2015,35(3):527-537.

[12] 何耀耀,闻才喜,许启发,等.考虑温度因素的中期电力负荷概率密度预测方法[J].电网技术,2015,39(1):176-181.

[13] 曾 鸣,吕春泉,田 廓,等.基于细菌群落趋药性优化的最小二乘支持向量机短期负荷预测方法[J].中国电机工程学报,2011,31(34):93-99.

[14] 马星河,闫炳耀,唐云峰,等.基于优选组合预测技术的中长期负荷预测[J].电力系统及其自动化学报,2015,27(6):62-67.

[15] 莫若慧,符子星,曾 炎,等.台风天气下电网负荷对气象因素的敏感度分析[J].南方电网技术,2015,9(2):79-83.

[16] PAO Yoh-Han,PARK Gwang-Hoon,SOBAJIC D J.Learning and Generalization Characteristics of the Random Vector Functional-link Net[J].Neurocom-puting,1994,6(2):163-180.

[17] IGELNIK B,PAO Y H.Stochastic Choice of Basis Functions in Adaptive Function Approximation and the Functional-link Net[J].IEEE Transactions on Neural Networks,1995,6(6):1320-1329.