基于平衡系数的加权网络改进k核算法

王 棹,张曦煌

(江南大学 物联网工程学院,江苏 无锡 214000)

0 概述

复杂网络节点重要性研究是复杂网络理论中十分重要的部分,对不同网络的研究已经发展出很多新的理论[1-3]。这些相关理论已应用到社交网络[4]、传播网络[5]、计算机网络[6]等各种网络的分析中,并取得了科学的可靠的结果。由于复杂网络中的节点数目十分巨大,一个网络中有成百上千个甚至数十万个网络节点,如何高效准确地识别出其中的重要节点变得十分困难,这些关键的节点处于网络中十分重要的位置,对整个网络的抗毁性[7-8]有至关重要的作用。

目前,在复杂网络理论中节点重要性的评价方法主要有节点度[9]、网络介数[10]、接近中心和PankRank[11]。节点度只反映了节点在网络局部的重要性。介数和接近中心算法从网络全局角度出发,对节点在网络中所处的位置给出了较为准确的节点重要性评价,但是由于它们都需要计算所有节点到其他网络节点的最短路径[12],因此算法复杂度非常高。文献[13]提出了基于节点重要度贡献的节点重要性算法,给出了基于m阶邻居节点重要度贡献的复杂网络节点重要度计算方法,该算法取得了较好的实验结果,但不适用于加权网络。文献[14]在文献[12]的基础上提出了适用于加权网络的节点重要度改进算法,但由于算法复杂度高,因此不适合用来分析大型网络。PankRank算法是由谷歌公司提出的基于随机游走的网页重要性排序算法,该算法主要应用在互联网领域,且不适合用来分析加权网络。文献[15-16]提出了k核算法,认为网络传播动力学中最重要的节点并非传统的度最大或介数最大的 Hub 节点,而是具有最大k核值的节点。该算法从网络整体布局的角度提出了节点重要性的评价方法,具有较低的算法复杂度,能快速地给出超大型网络的节点重要性评价参数。但该算法同样只适用于无权网络。

针对以上算法的问题,本文在k核算法的基础上,提出基于平衡系数的复杂加权网络改进k核算法。该算法引入权重值重新定义了更适用于加权网络的节点k核值指标。将权重值对评价结果的影响定量化,并调整平衡系数以适应不同网络的特点。

1 复杂网络

1.1 接近中心算法

节点的接近中心是它到其他所有节点的最短距离之和的倒数,表达式为:

(1)

其中,N是节点总数,kij是从节点vi到节点vj的最短路径长度。CC值越大,则节点在全局网络中居于中心位置的程度也越大。

1.2 k核算法

k核算法通过递归地移去网络中所有度值小于或等于k的节点来描述网络结构特征,揭示网络层次性质。

假设网络G=(V,E) 是由|V|=N个节点和|E|=E条边所组成的一个无向网络,则k核的定义如下:由集合推导出的子网络H=(C,E|C),当且仅当对C中的任意节点V,其度值均大于k,具有这一性质的最大子网络的补集被称为k-核,简称Ks,其分解示意图如图1所示。

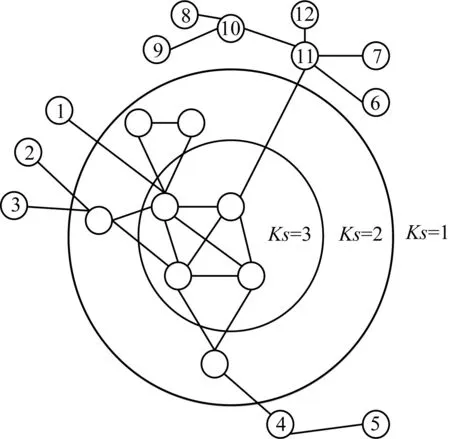
图1 k核算法分解示意图

该网络被划分为3层不同的核:最外层的节点k核值为1,它们处于整个网络的边缘,对网络的影响较小。中间层的节点k核值为2,最里层的节点k核值为3,它们是处于网络中心的节点,对整个网络的连通性和完整性有巨大的影响。但是由于k核算法只注重于寻找网络中最关键的节点,因此在k核分析中存在大量k核值相同的节点。例如图中的节点1～节点12的k核值均为1。这也是k核算法的不足之处。

1.3 基于平衡系数的改进k核算法

1.3.1 基本思路

在Kitsak 等人的研究基础上,本文提出一种针对复杂加权网络的k核改进算法。在加权网络中节点的度k′和k″定义如下:

(2)

(3)

其中,ki表示节点i的度,wij表示与节点i相连的边的权重。α和β是在改进k核算法中加入的2个调整参数,用来调节节点的k核值和连边权重值对改进k核值的影响程度。在选择α和β的值时,要有一定的科学依据,合理地选择这2个值,才能使算法得出的结果具有与实际情况相符的科学性。当α和β的取值发生变化时,反映加权网络节点重要性的k′核值相应地也随之变化。因此,本文定义了k″值,从该值的定义中可以看出,无论k′如何变化,k″都能用来定量衡量每个节点的重要性在整个网络中的定位,其值类似于反映一个数值在所有数值中所占有的百分比。因此,在实际网络分析中,当α和β的取值变动时,可以用k″来准确地反映节点重要性的变化情况。

为了确定α和β的取值关系,本文定义了平衡系数E这一概念,其定义如下:

(4)

其中,k表示网络中节点的k核值,wij表示网络中节点的连边权重值之和。通过计算网络中这2个值的总和和合理地设置平衡系数,能科学地确定k核值和连边权重在节点重要性评价参数中的权重。在不同的网络中,可以根据实际网络的情况调整这一系数。例如在城市路网建设规划时,节点连边的权重值即车流量应不超过道路设计的最大承载量,各节点的度值一般不超过4。在分析水网情况时,连边权重值也应考虑到该河流的最大泄洪能力。在本文实验中,平衡系数的取值将会多样化,用以分析该系数对最终实验结果的影响。当E=1时:

(5)

经过平衡系数调整之后的权重值为:

(6)

在调整之后的网络中,网络所有节点的度值与所有连边之间的权重值在数学意义上具有同样的重要性。

1.3.2 算法步骤和复杂度分析

改进的加权网络节点重要性算法步骤如下:

步骤1选出网络中节点度为1的点并将这些点从网络中删除。

步骤2在删除步骤1中节点后得到的新的网络图中找出度为1的网络节点。

步骤3重复步骤2直至网络图中找不出度为1的节点。步骤1～步骤3中找出的所有节点的k核值均为1。

步骤4将网络图中所有k核值为1的点从网络图中删除,得到一个新的网络图,并寻找该网络图中节点度为2的点。

步骤5重复步骤2和步骤3,直至网络图中不再有度为2的节点。步骤4和步骤5中找出的节点的k核值均为2。

步骤6按照相同的方法确定网络中所有节点的k核值。

步骤7计算出网络中所有节点的k核值的总和与网络中所有边的权重值之和。

步骤8确定平衡系数E的值,并计算权重值之和与k核值之和的比值,将每条边的权重值除以这个比值得到新的权重。

步骤9计算得到加权网络中的节点k核值k′并进一步计算出k″。

由以上步骤可以看出,改进k核算法并没有改变k核算法的算法复杂度O(n),只是在得到节点的k核值后根据式(2)算出节点的改进k核值k′,并通过式(3)算出k″。这2个步骤的算法复杂度均为O(n),因此适用于加权网络的改进k核算法的算法复杂度仍为O(n)。而传统的介数中心算法,接近中心算法的算法复杂度为O(n3)。因此,改进k核算法更适合用来分析大型网络的节点重要性。

2 实验结果与分析

本文实验加权网络图如图2所示。该加权网络由34个节点和70条边构成。实验分别应用接近中心算法、k核算法以及改进k核算法对网络中的节点进行分析。在实验中,改进k核算法的平衡系数E=1,在本文后续的实验中,将会改变改进k核算法中平衡系数E的取值,对比不同平衡系数取值对改进k核算法最终排序结果的影响。并分析网络中各类节点在平衡系数发生改变时的重要性变化趋势。本文加权实验结果如表1所示。

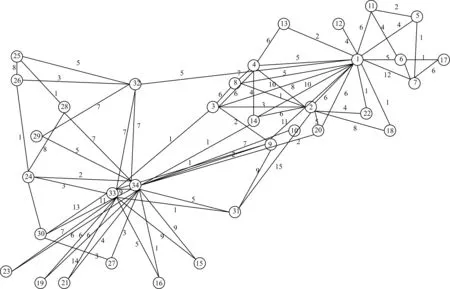
图2 本文实验加权网络图

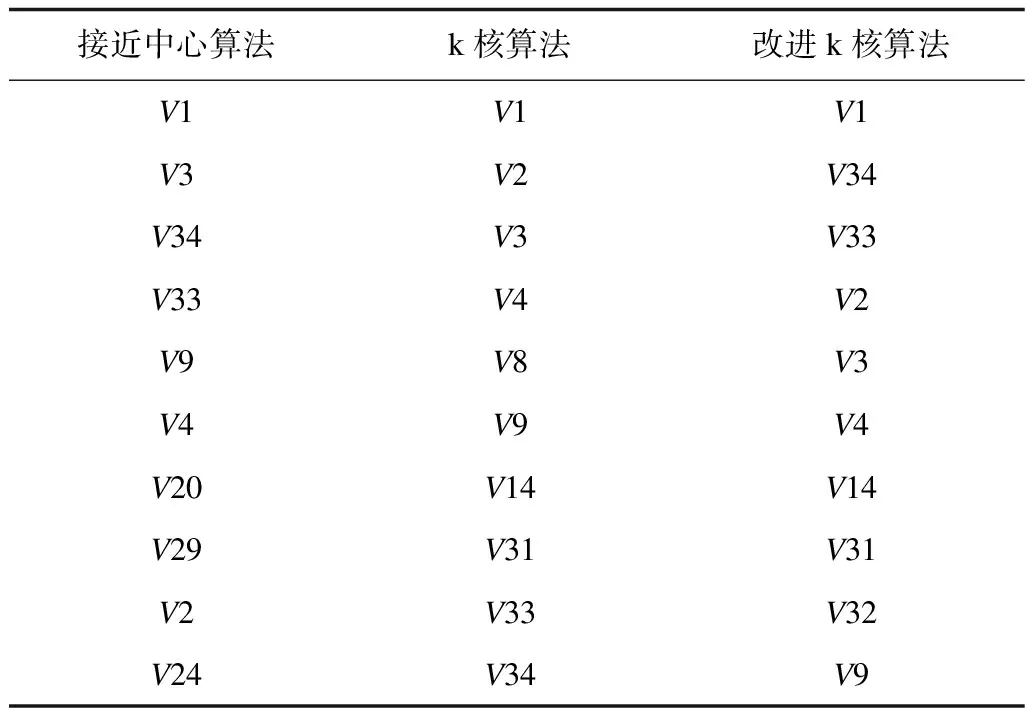
接近中心算法k核算法改进k核算法V1V1V1V3V2V34V34V3V33V33V4V2V9V8V3V4V9V4V20V14V14V29V31V31V2V33V32V24V34V9

表1中分别给出了3种算法的节点重要性排序。由于节点数目较多,因此表中只列出了最关键的10个节点及其顺序。可以比较明显地看出3种算法对关键节点的筛选结果有明显的不同。除了V1节点都排在首位之外,其余节点的位置都不相同。其中考虑网络连边权重的改进k核算法与原k核算法的结果也出现了较大不同。在原k核算法中,也存在相似节点的重要性难以区分的问题,改进k核算法则很好地解决了这个问题。

为了说明表1中3种算法得出的结果的科学性以及验证改进k核算法与原k核算法、接近中心算法相比的优势。在实验中依次将3种算法最重要的10个关键节点从网络图中移除,分别得到3种算法在依次移除节点之后的10张网络图,从移除节点后网络中的失效节点数、网络中最大连通子图的节点数、网络损失的连边权重这3个方面进行分析,得到的实验结果如图3～图5所示。从图3～图5中可以看出,当依次从网络图中移除关键节点后,网络的失效节点数、最大连通子图节点数、网络损失连边权重都发生了很大变化。改进k核算法在移除关键节点后,失效节点数量多于接近中心算法和原k核算法。最大连通子图节点数明显少于原k核算法,与接近中心算法在移除关键节点后的最大连通子图节点数相当。

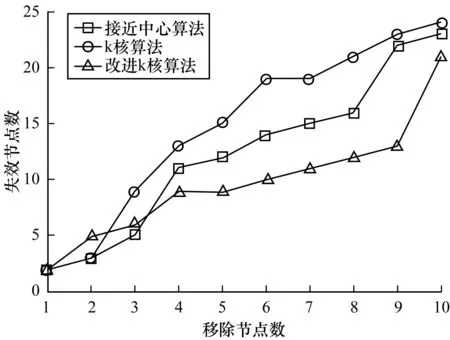
图3 移除节点数与失效节点数关系

图4 移除节点数与网络最大连通子图节点数关系

图5 移除节点数与网络损失连边权重关系

在图5中,改进k核算法在移除节点之后损失的连边权重一直高于原k核算法和接近中心算法。图3～图5的实验结果表明,改进k核算法移除节点后对网络的破坏效果最明显,因此,这些节点在网络中的位置更重要,特别是与原k核算法相比,在3个参数的比较中都较原算法提高了很多,并在整体上优于接近中心算法的结果。

在实验中,改进k核算法的平衡系数值E=1,在加权网络分析中,权重对网络的影响不尽相同,因此在评价网络节点重要性时,权重的参考量是一个不完全定量因素,改进k核算法引进平衡系数E这一参数来描述这一变化,为了研究平衡系数E的取值对网络节点重要性评价的影响,在后续实验中,将平衡系数的取值多样化,从E=1/32依次乘2至E=32进行11次实验结果比较,得到的实验结果如图6所示。从图6中可以看出,当平衡系数取值发生变化时,相应地节点的重要性参数值也发生变化,节点连边较多,权重较大的节点的重要性相对下降,其他节点的重要性相对上升。为了更直观地分析各个节点的重要性变化情况,实验选取几个变化较为明显的节点,例如重要性下降最明显的节点V1、V34、V33,重要性上升最明显的节点V5、V11、V29,以及在平衡系数发生变化时,重要性排序发生改变的几个节点进行两两比较的定量分析,后续实验的结果如图7～图9所示。

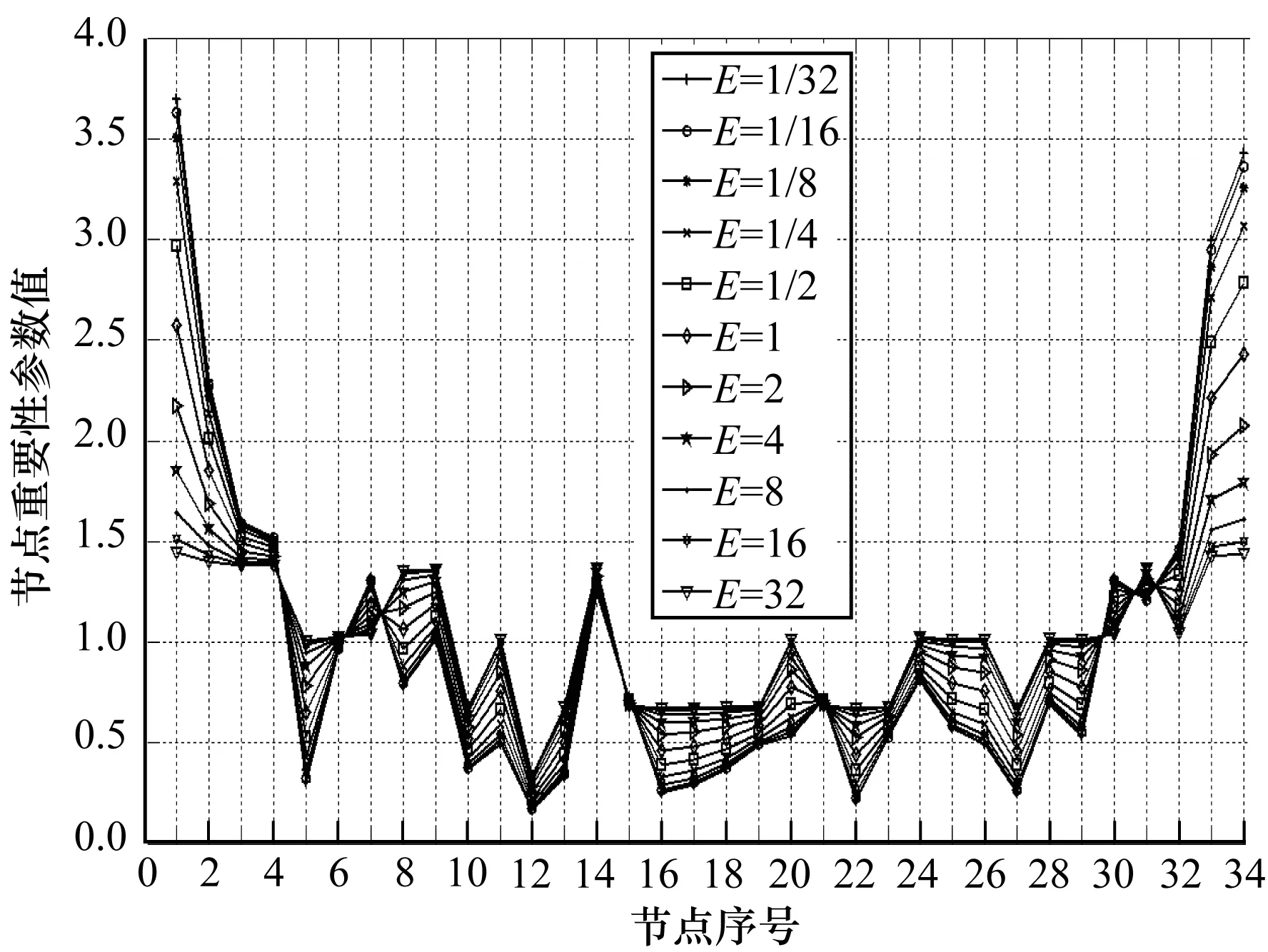
图6 不同平衡系数的改进k核算法结果

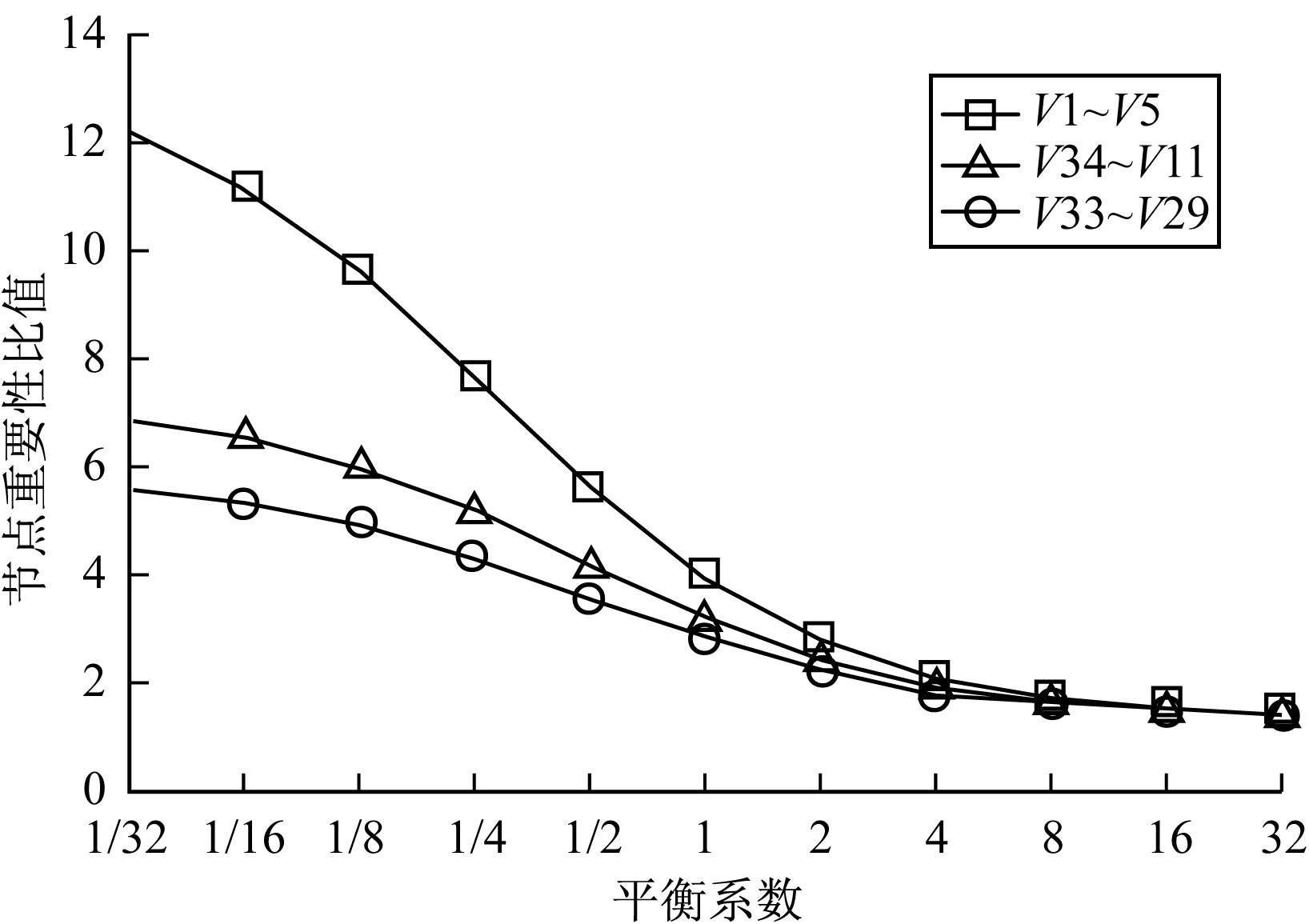
图7 节点重要性分析实验结果1

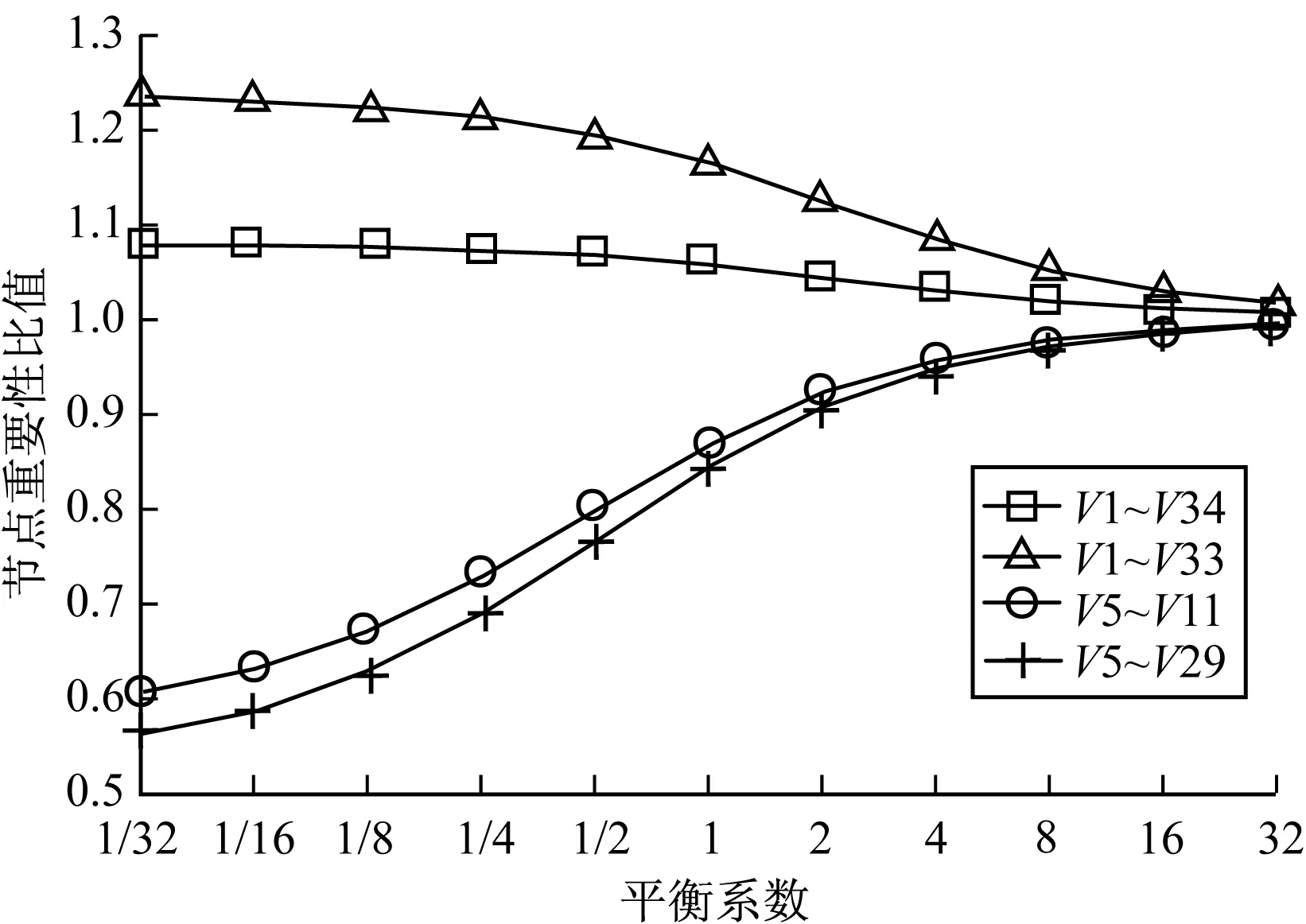
图8 节点重要性分析实验结果2

图9 节点重要性分析实验结果3

从图7可以看出,随着平衡系数的增大,k核值在节点重要性评价参数中的比重逐渐提高,权重值的比重相应降低,V1、V34、V33等权重值较大的节点的重要性逐渐下降,V5、V11、V29等权重值较小的节点的重要性逐渐上升。

从图8中V1与V34、V33的比值曲线中可以看出,随着平衡系数的增大,V1节点较V34、V33节点的重要性下降速度更快,V5节点较V11、V29节点的重要性上升速度更快,因此,V1节点与V5节点分别是平衡系数增大之后重要性变化最大的2个节点。

图9中比较了几个重要性相当的节点重要性变化关系,从图9中可以看出,当平衡系数较小时,在算法得出的结果中,V32、V7、V30节点更为重要,随着平衡系数的增大,比值曲线都开始发生变化,当曲线经过y=1这条线时,2个节点的重要性次序发生变化,V31、V9、V14节点的重要性超过V32、V7、V30。V8节点的重要性则随着平衡系数的增大逐渐逼近节点V9,即比值曲线无限趋近于1。

在平衡系数发生变化的过程中,大部分节点的重要性并没有发生极大变化,因此,在节点重要性排序中并没有与平衡系数为1时的排序有太大的差距,即使改变平衡系数,改进k核算法得出的节点重要性排序结果相比原k核算法也有极大地提高,比最短路径算法得出的结果更具科学性和合理性。

3 结束语

本文提出一种适用于加权网络的改进k核算法。该算法可解决k核算法只能适用于无权网络以及k核值差距过小无法区分节点重要性的问题。在本文实验中,改进k核算法在与k核算法、接近中心的算法比较中得出更准确的结果。该算法在依次删除改进k核算法结果中最重要的10个节点之后,网络受到的破坏程度在失效节点数、最大连通子图、网络损失权重3项指标上均比k核算法有了大幅提高,整体优于接近中心算法。在后续实验中,平衡系数的改变相应地改变了算法最终的结果,并分析了节点重要性的变化。但针对不同加权网络,如何科学地调整平衡系数以取得更精确的实验结果,将是下一步的研究方向。

[1] 任晓龙,吕琳媛.网络重要节点排序方法综述[J].科学通报,2014,59(13) :1175-1197.

[2] 杨 博,陈贺昌,朱冠宇,等.基于超链接多样性分析的新型网页排名算法[J].计算机学报,2014,37(4):833-847.

[3] 段松青,吴 斌,王 柏.TTRank:基于倾向性转变的用户影响力排序[J].计算机研究与发展,2014,51(10):2225-2238.

[4] SEN Pei,LEV M,JOSE S,et al.Searching for Superspreaders of Information in Real-world Social Media[J].Scientific Reports,2014(4):55-67.

[5] 李 栋,徐志明,李 生,等.在线社会网络中信息扩散[J].计算机学报,2014,37(1):189-206.

[6] 杨 博,陈贺昌,朱冠宇,等.基于超链接多样性分析的新型网页排名算法[J].计算机学报,2014,37(4):833-847.

[7] 马润年,文 刚,邵明志,等.基于抗毁性测度的赋权网络抗毁性评估方法[J].计算机应用研究,2013,30(6):1802-1804.

[8] 李文锋,符修文.无线传感器网络抗毁性[J].计算机学报,2015,38(3):625-647.

[9] 闵 磊,刘 智,唐向阳,等.基于扩展度的复杂网络传播影响力评估算法[J].物理学报,2015,64(8):387-397.

[10] GOH K I,OH E,KAHANG B,et al.Spectra and Eigenvectors of Scale-free Networks[J].Physical Review E Statistical Nonlinear & Soft Matter Physics,2003,67(2).

[11] BRYAN K,LEI S E T.Eigenvector:The Linear Algebra Behind Google[J].SIAM Review,2006,48(3):569-581.

[12] 唐晋韬,王 挺,王 戟.适合复杂网络分析的最短路径近似算法[J].软件学报,2011,22(10):2279-2290.

[13] 张喜平,李永树,刘 刚,等.节点重要度贡献的复杂网络节点重要度评估方法[J].复杂系统与复杂性科学,2014,11(3):26-32,49.

[14] 王甲生,吴晓平,廖 巍,等.改进的加权复杂网络节点重要度评估方法[J].计算机工程,2012,38(10):74-76.

[15] KITSAK M,GALLOS L K,HAVLIN S,et al.Identifying Influential Spreaders in Complex Networks[J].Nature Physics,2010,6(11):888-893.

[16] 任卓明,刘建国,邵凤,胡兆龙,郭 强.复杂网络中最小K-核节点的传播能力分析[J].物理学报,2013,62(10):474-479.