基于RBF网络的城市垃圾产量预测及可视化
2018-03-02秦绪佳郑红波张美玉浙江工业大学计算机科学与技术学院浙江杭州310023
秦绪佳,彭 洁,徐 菲,郑红波,张美玉 (浙江工业大学计算机科学与技术学院,浙江 杭州 310023)
城市垃圾指大量以固态形式呈现的废物混合物.随着市民消费水平整体提高,日渐增长的垃圾排放量致使“垃圾围城”的现象成为全球趋势.日前,大量露天堆放的垃圾严重影响居民生活、城市容貌、经济建设、资源永续和生态环境等.因此,控制未来城市垃圾产量成为各环保组织的一个重要研究课题.
研究我国城市垃圾产量的变化规律及发展趋势,不但能为城市环境规划运行和监管等决策提供数据支持,还能为垃圾废物的清扫、运输和处理拟定合理的实施方案.可见,有必要建立合适的预测模型来高效合理的预测未来几年的垃圾排放量.
目前,国内常用的预测方法包括灰色分析模型、BP神经网络模型、多元线性回归模型、时间序列法等.依据全省管理现状,文献[1-2]通过建立灰色分析模型分别对辽宁省未来2012~ 2020年及西安市2011~2020年的生活垃圾产量进行预测,模型精度较高,方法合理且有意义.基于传统BP神经网络,文献[3]基于污染物浓度及可见度,建立风险神经网络预测模型,对天津市历年气象数据检验并预测.文献[4]以深圳市2004~2012年的生活垃圾产量为样本,建立基于时间序列分析的ARIMA模型.方法较好地预测生活垃圾产量的季节性变化规律.此外,国外学者Noori等[5]将人工智能技术中向量机的概念应用于垃圾预测,但该方法发展不成熟,尚处于摸索阶段,存在许多不确定因素.目前,现存的预测模型大都存在相同的特点,即根据未筛选的变量集或基于现状,主观地筛选变量作为拟影响因素,来建立垃圾产量的预测模型.
互信息用来度量多个变量间的亲密度,即互相包含的信息含量.RBF网络衍生于数值分析中初次提到的多变量插值的径向基算法[6].与其他多层反向传播网络类似,它是一种包含输入层、隐含层和输出层的高效的三层前馈式网络拓扑结构.RBF网络不但收敛速度相对较快,而且能以不同精度逼近连续函数.
为克服现存方法精度不高,计算量大及未筛选影响因素等问题,本文提出一种基于互信息确定影响因素,径向基函数网络训练及相对平均误差反向修正建立预测模型的新方法.实验结果显示,采用本文建立的RBF网络预测模型对全国各省市城市垃圾排放量进行预测,不但具有收敛速度快和预测精确度较高等优势,还具有一定的理论和实践意义.
1 基于互信息的垃圾产生量影响因素的确定
据统计,对预测垃圾未来产量的影响要素有很多,比如内在因素、自然环境以及社会经济等[7].本文根据内在因素建立各省份垃圾排放量的预测模型,其中预拟影响因素包括地区生产总值、居民消费水平、社会消费品零售值、金融及建筑业增加值等18项,预拟定影响因素及2014年部分省垃圾产量[8](部分数据)如表1所示.

表1 垃圾产生量及拟定影响因素(部分数据)Table 1 Waste production and possible influence factors (partial data)
合适的变量集可直接决定模型建立的精确度.一般地,相关变量有利于建立准确的预测模型,而冗余变量不但增加模型计算的复杂度,而且掩盖变量间的相关作用.为降低冗余变量带来的干扰,建立高效的预测模型,本文利用多变量间的相关性分析确定一个变量关系最密切的子变量集.一般地,可以采用独立成分分析(ICA)[9]、主成分分析(PCA)、典型相关分析(CCA)、聚类分析和互信息等方法进行多元变量的相关性分析[10].其中互信息起源于信息论中的熵,即信号在传输过程中丢失的信息量,常被用来度量多个变量间的亲密度.该方法不但能定性地推测变量间的关系变化趋势,还能定量地确定变量间的具体数值关系.
下面将基于K-近邻估计互信息,并根据互信息筛选影响城市垃圾产生量的主要因素.
1.1 K-近邻的互信息估计
定义两个连续变量X和Y,假设µx(x)、µy(y)和u( x, y)依次是X、Y的边际密度函数和联合密度函数.根据信息论的相关理论,X和Y之间的互信息可写成:

若上式I越大,说明变量X与Y亲密度越高,彼此的共同信息量越多.相反,若互信息I值越小,甚至为0时,说明这两个变量相互包含的信息含量很少,甚至相互独立.
此外,计算变量X、Y的熵及联合熵是估计互信息的另一种简便方法,如下式:

式中:

由于分别对边际密度函数和联合密度函数近似估计会带来较大误差,为克服这一缺点,Kraskov等[11]提出了基于K-近邻的互信息估计法来减少误差.该算法的主要思想是:假设连续变量X和Y构成向量空Z=(X, Y),则向量空间内每个样本点zi=(xi, yi)的K-近邻可利用最大范数计算:

在空间Z上,假设样本点zi=(xi, yi)到其k-近邻距离为ε(i)/2,且该点投影到X轴和Y轴的距离分别为εx(i )/2和εy(i)/2.在X空间中,到xi的欧氏距离小于ε(i)/2的样本点的数目为nx( i);在Y空间中,到yi的欧氏距离小于ε(i)/2的样本点数目为ny(i).则X和Y的互信息可由以下公式估计:

式中:ψ(x)为digamma函数,简记为ψ(x)=Γ(x)-1dΓ(x)/dx ,该式满足ψ(x+1)=ψ(x)+1/x,ψ(1)≈-0.5772156.若将上述公式扩展到高维空间,多维变量间的互信息可表示为:

1.2 基于K-近邻的互信息的多变量选择
由于输入的多变量之间并非局限于线型关系,因此,为了分析不同输入变量对互信息量的影响,本文采用以互信息为基础的特征选择[12]算法分析多变量间的相关关系,进而识别并移除冗余、无关的变量.早期Battiti等[13]提出基于互信息的特征选择MIFS算法,随后大量改进的评价标准相继涌现,如MIFS-U[14]、mRMR[15]、PMI[16]、NMIFS[17]、CMINN[18]等.下文引入多变量信息作为选择相关变量的评价标准[19-20],即在高维空间中多个变量间的互信息.在该方法中,对于给定的输入特征变量,该方法既考虑与输出特征变量也考虑与已选特征变量的关系.
假设3个连续变量X、Y和Z的互信息记为I( X; Y;Z),则其可表示为:

式中:上式前项称为条件互信息量[21],即在已知某个条件Z的情况下,变量X和Y通讯传递后获得的信息量.条件互信息可表示为:

因此,条件互信息一定为非负值,结合上节基于K-近邻的互信息估计,该条件互信息估计可写为:
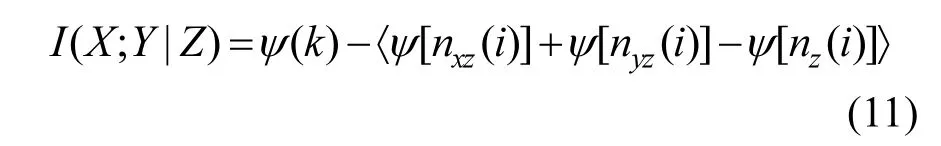
根据上述公式(2)、(9)和(11)可以估计连续变量X、Y和Z的互信息.但是,与条件互信息不同,多变量互信息的值可能为正值也可为负值.当多信息I>0时,说明特征变量X和Y互补;当多信息I<0时,意味着Z是冗余变量,故当添加Z作为条件时反而降低X与Y的依赖程度;当多信息I=0时,表示Y和Z之间的依赖关系与X基本无关.依据上述性质,本文关于多特征变量选择评价标准的定义如下:

式中:X为待选变量;Y为已选变量;Z为类变量;β为用户自定义量.上式用来衡量变量Y和Z的依赖性受变量X影响的程度.当满足上述公式时,则认为X是相关变量,否则是冗余变量.
综上,假设算法的输入变量分别是: U=D(F,C)为训练数据集,F为所有输入特征变量,C为类变量;输出变量是选择特征集S,则基于 K-近邻互信息方法确定影响因素的步骤如表2:

表2 基于K-近邻互信息的确定影响因素算法Table 2 Algorithm of determining influence factors based on k-neighbor mutual information
2 基于RBF网络的城市垃圾产量预测
与其他多层反向传播网络类似,径向基网络函数是一种包含输入层、隐含层和输出层的收敛速度很快的3层前馈式网络拓扑结构,它不但有可能满足实时性要求,而且能以不同精度逼近连续函数.本文关于预测城市垃圾产生量的RBF网络结构如图1所示.

图1 RBF网络Fig.1 Radial basis function network
在上述模型中,输入层是由样本数据构成,输出单元是对隐单元激活后的简单线性函数.通过对激活函数参数的调整,隐含层神经元不但能将低维空间模式转成高维空间,还能将非线性映射转换成线性映射.当输入样本值越邻近基函数的中心,隐含层单元的激活程度越高、权重越高,故RBF网络的输出值为:
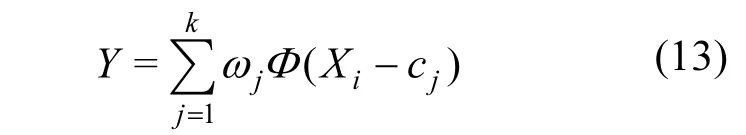
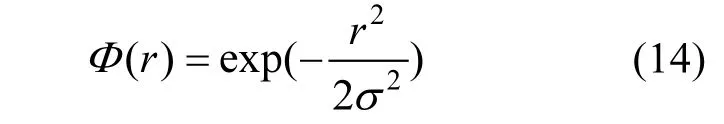
本文采用两阶段预测垃圾产量的方法,第一阶段基于RBF网络训练出初始预测模型.该阶段首先根据改进的K-means++算法确定径向基函数网络的隐含层节点中心,然后利用梯度下降法调节基函数中心c、扩展常数σ和权值w等参数.第二阶段利用相对平均误差对初始模型反向误差修正获得垃圾产生量的最终预测模型.
2.1 数据预处理
考虑到影响城市垃圾产生量的因素的基本量纲不同,为消除不同量纲对实验结果造成的影响,首先对所有输入数据进行归一化预处理,即把所有因素转化为0~1之间的数据.通过归一化不仅提高模型的精度,也增加模型收敛速度.我们采用线性变换对所有影响因素进行归一化:

式中:min和max分别为训练样本数据的最小值和最大值.此外,实验结束时还通过反归一化恢复数据.
2.2 确定初始参数
2.2.1 确定聚类中心 本文基于一种改进的方法——K-means++聚类[22]算法确定径向基函数的中心并且以自适应的方式确定隐含层单元数量k.替代传统的随机选取,利用K-means++聚类网络初始化k个聚类中心,然后根据K-means方法重新调整聚类中心.关于确定初始聚类中心算法如表3所示,自适应确定隐含层单元数量k值的方法如表4所示:
2.2.2 确定扩展常数 根据上节可确定的每个径向基函数的中心距离其他径向基函数中心的最短距离di=mjin(ci-cj),j=1,2,...k ,其中ci为径向基函数中心,且j≠i,λ为重叠系数,则扩展常数σi为可表示为:

2.2.3 确定权值 本文假设随机给定[-1,1]的数值确定隐含层节点至输出层节点之间的权值wi( i=1,2,...k ).
2.3 网络训练及参数修正
根据RBF网络拓扑结构可知,通过调节最小化目标函数中隐单元中心、扩展常数和权值来实现梯度网络训练.神经网络学习的目标函数为:


表3 确定初始聚类中心的算法Table 3 Algorithm of determining initial clustering centers

表4 自适应确定k值方法Table 4 Adaptive determination of k value method
式中:E为径向基函数的全局误差;k为隐含层节点的数量;ei为第i个样本点的预测模型输出值和实际值的误差,计算如下:
到0.93 V,体偏置从0.6 V到-1.8 V,而PMOS阈值电压从-0.32 V降低到-1.01V,体偏置从-0.6 V到1.8 V。

式中:yi为样本实际值;f( xi)为该样本经RBF网络训练的输出值;m为输入样本的数量;wj为隐含层到输出层单元的权重,Φ(Xi-cj)为基函数,本文选用高斯函数作为激活函数;Xi为第i个样本的输入值;cj为第j个径向基函数的中心.
为使目标函数E最小,本文采用梯度下降法调节径向基函数中心c、扩展常数σ和权值w:

式中:η为学习率,采用自适应调节学习率的方法,当前迭代次数记为i,总共迭代次数记为n,学习率与迭代次数间的关系可表示为:

重复上述过程,直至完成迭代,或当前预测值与真实值的方差小于用户定义的最小方差,即S2<,则迭代结束,初始模型训练完成.
2.4 误差反向修正
采用上述方法对全国各省市垃圾产量建立径向基网络函数获得初始预测模型,但不同省份对径向基函数网络的适应性不同.下面利用相对平均误差反向修正初始结果获得最终预测模型.具体修正方式如下:

2.5 整体算法流程
综上所述,基于径向基函数(RBF)网络建立全国城市垃圾排放量预测模型的基本思路如下:已知样本输入数据,通过径向基函数网络构造的线性公式,利用样本预测值和实际值间的误差调节径向基函数中心、扩展常数和权值,经过误差反向修正,获得最终预测模型.模型预测流程如图2所示:

图2 预测模型流程Fig.2 The flow chart of the prediction model
3 结果分析及可视化
选取我国各省2004~2011年垃圾产生量的影响因素和2006~2013年的垃圾产生量的实际数据作为网络训练样本,2012~2013年的影响因素和2014~2015年的垃圾量数据为模型检验样本,并利用该模型预测及可视化全国各省市2017~2018年的垃圾产量.
首先对18个拟影响因素(表1中仅列出了其中9个)建立K-近邻估计互信息,根据互信息筛选出对城市垃圾产生量有主要影响的8个因素,即预测模型的输入变量.确定的影响因素分别为常住人口、地区生产总值、社会消费品零售值、金融业增加值、工业增加值、批发和零售业增加值、住宿和餐饮业增加值和第三产业增加值.其中,社会消费品零售值与城市垃圾产生量负相关,其他项与城市垃圾产生量正相关.
根据RBF网络的拓扑结构,采用两阶段的径向基函数网络对垃圾产量进行预测,并以Choropleth地图对全国各省的垃圾产生量进行可视化.Choropleth地图(也称为分级统计图)是指对数据属性值划分为不同等级,并选择合适的色级,以反映数据在地理上的分布差异.通过比较2014~2015年全国各省检验样本基于RBF模型的预测值和实际输出值,获得模型的相对误差及平均相对误差.由于检验样本数据量较大,表5仅列出部分省市数据、样本最优相对误差和平均相对误差.表中平均相对误差为所有样本数据相对误差的平均值.图3为浙江省垃圾产量预测变化曲线.图4为基于Choropleth地图我国2015~2016年垃圾产生量的分布图及2017~2018年的垃圾产生量预测分布.

图3 浙江省垃圾产生量预测变化曲线Fig.3 The prediction curve of waste production in Zhejiang province
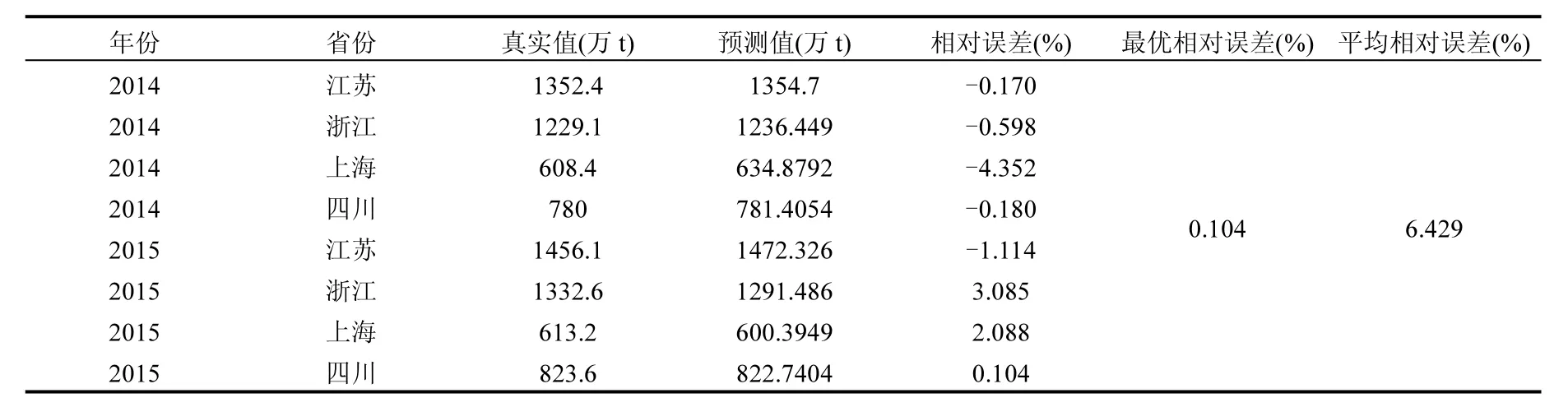
表5 实际与预测数据对比(部分数据)Table 5 Comparison between actual and predicted data (partial data)
实验结果发现:由图4所示,近几年广东省垃圾产量在全国范围内一直位居首位.整体而言,华东地区垃圾产生量较多且有明显增多的迹象.大部分省市垃圾产生量有略微的增长,其中山东省增长最快;少量省市垃圾产生量降低,其中黑龙江和吉林减少最明显.由图3所示,浙江省垃圾产量模型曲线拟合比较好.
对比现有相关文献,文献[2]采用GM(1,1)模型预测建成土地面积及居民可支配收入的相对平均误差为5.7%和11.11%.文献[4]建立ARIMA模型的相对平均误差为5.288%,但最大绝对百分比误差高达 25.775%.本文通过对2014~2015年全国各省市检验样本基于RBF模型得到的预测值和实际输出值的比较,理论上计算得出相对平均误差是6.43%,相当于预测精度为93.57%.其中,相对平均误差最优值为0.1%,相当于预测精度为99.9%. 近些年,随着城市生活垃圾管理体系的不断变化,垃圾的处理方式在不断升级,从露天堆积和焚烧、随地填埋到资源回收再利用,再到尽力减少源头垃圾量.由于本文目标是预测2017~2018年的垃圾产生量,一般地,在短期内垃圾的管理方式变化基本不大,故对本文的预测模型影响不大.因此,本文建立的两段式径向基函数网络模型的预测精度较高,能较好的对城市垃圾的产生量进行预测.

图4 基于2015~2018年Choropleth的垃圾产生量可视化分布Fig.4 The visualization of waste production based on Choropleth from 2015 to 2018
4 结论
运用具有较强非线性处理能力和逼近能力的径向基函数网络建立预测模型,并预测及可视化我国2017~2018年全国各省市垃圾排放量.
由于城市垃圾产量受到许多因素的影响,合适的变量集可直接决定模型的预测精度.故本文首先基于K-近邻互信息的多变量选择特征准则剔除冗余、无关因素,从18个拟影响因素中确定了8个影响垃圾排放量的因子;然后基于RBF网络训练得出垃圾产生量初始预测模型,并对初始预测结果误差反向修正获得最终预测模型.通过比较检验样本预测值和实际观测值,大部分省市垃圾产生量仍有略微的增长,尤其广东省稳居首位,相反,黑龙江和吉林等少量省市垃圾产生量有所降低.
[1] 王东明,吕洪涛.基于灰色预测模型的辽宁省城市生活垃圾产生量预测 [J]. 环境保护与循环经济, 2013,33(4):30-31+44.
[2] 李艳平,麻敏洁,鲁来凤.基于多模型拟合的西安市生活垃圾量预测 [J]. 计算机工程与应用, 2015,(6):222-226.
[3] 王 恺,赵 宏,刘爱霞,等.基于风险神经网络的大气能见度预测 [J]. 中国环境科学, 2009,29(10):1029-1033.
[4] 吴灵玲,卢加伟,廖利,等.基于ARIMA模型的生活垃圾产生量预测 [J]. 环境卫生工程, 2013,(5):1-4.
[5] Noori R, Abdoli M A, Ghasrodashti A A, et al. Prediction of municipal solid waste generation with combination of support vector machine and principal component analysis:a case study of mashhad [J]. Environmental Progress & Sus-tainable Energy,2009,28(2):249-258.
[6] 郑剑锋,焦继东,孙力平.基于神经网络的城市内湖水华预警综合建模方法研究 [J]. 中国环境科学, 2017,37(5):1872-1878.
[7] 何德文,金 艳,柴立元,等.国内大中城市生活垃圾产生量与成分的影响因素分析 [J]. 环境卫生工程, 2005,13(4):7-10.
[8] 国家统计局.中国统计年鉴 [M]. 北京:中国统计出版社,2016:71-612.
[9] Lee T W. Independent Component Analysis: Theory and Applications. Boston: Kluwer Academic Publisher, 1998.
[10] 王展青.核统计成分分析及其在人脸识别中的应用研究 [D].华中科技大学, 2008.
[11] Alexander Kraskov, Harald Stogbauer, Peter Grassberger.Estimating mutual information [J]. Physical Review E. 2004,69(6):066138.
[12] 边肇祺,张学工.模式识别 [M]. 北京:清华大学出版社, 2000:176-177.
[13] Battiti R. Using mutual information for selecting features in supervised neural net learning. [J]. IEEE Transactions on Neural Networks, 1994,5(4):537-550.
[14] Kwak N, Choi C H. Input feature selection for classification problems. [J]. IEEE Transactions on Neural Networks, 2002,13(1):143-159.
[15] Peng H, Long F, Ding C. Feature Selection Based on Mutual Information: Criteria of Max-Dependency, Max-Relevance, and Min-Redundancy [J]. IEEE Transactions on Pattern Analysis &Machine Intelligence, 2005,27(8):1226-38.
[16] May R J, Maier H R, Dandy G C, et al. Non-linear variable selection for artificial neural networks using partial mutual information [J]. Environmental Modelling & Software, 2008,23(10/11):1312-1326.
[17] Estévez P A, Tesmer M et al. Normalized mutual information feature selection [J]. IEEE Transactions on Neural Networks,2009,20(2):189-201.
[18] Tsimpiris A, Vlachos I, Kugiumtzis D. Nearest neighbor estimate of conditional mutual information in feature selection [J]. Expert Systems with Applications, 2012,39(16):12697-12708.
[19] Mcgill W J. Multivariate information transmission [J].Psychometrika, 1954,19(2):93-111.
[20] Vergara J R, Estévez P A. A review of feature selection methods based on mutual information [J]. Neural Computing and Applications, 2014,24(1):175-186.
[21] Tsimpiris A, Vlachos I, Kugiumtzis D. Nearest neighbor estimate of conditional mutual information in feature selection [J]. Expert Systems with Applications, 2012,39(16):12697-12708.
[22] Arthur D, Vassilvitskii S. k-Means++: the advantages of careful seeding, in: SODA ’07 [C]. Proceedings of the Eighteenth Annual ACM-SIAM Symposiumon Discrete algorithms, Society for Industrial and Applied Mathematics, 2007:1027-1035.
