机场跑道毁伤效果评估及功能恢复模型

康元基，董 辉，陈子匀，吴长宇

（解放军66136部队，北京 100043）

0 引言

现代高科技条件下的战争中，夺得制空权对战争胜负具有决定性意义。战争中，为压制空中力量，可集中火力对机场进行袭击和封锁。对于露天机场而言，由于其跑道面积较大并且暴露在地面，因此，最常见、最有效的打击手段之一就是破坏机场跑道，而如何对机场跑道的毁伤效果进行评估成为作战效果评估领域的研究热点。

目前，关于机场跑道毁伤效果评估的主要研究方向集中在如何利用遥感图像对机场的毁伤效果进行分析［1-4］以及对毁伤效果进行模拟计算［5-6，8］，而文献［7］中设计机场跑道毁伤效果评估系统框架，通过扫描最小起降窗口的方法定性评估毁伤效果。本文建立了机场跑道毁伤效果评估仿真模型，以多个基础数据库为支撑，在数学上严格描述了搜索最小起降窗口的算法，并对其精度与效率的关系进行计算，在此基础之上，设计了从被封锁机场最快恢复一个最小起降窗口的算法。

1 仿真模型建立

本文中仿真模型以多个基础数据库为支撑，实现毁伤效率评估模型和功能恢复时间评估模型两大部分。模型的整体结构如下页图1所示。

基础数据库模板中包括：1）各类机型数据库，存储各类机型的尺寸、最小起降窗口等信息；2）全球机场数据库，存储各个机场的长宽、跑道材质、海拔、支持起降的机型等信息；3）弹目效能数据库，存储弹目类型、毁伤半径、圆概率误差等信息；4）路面修复数据库，存储各类路面的修复方法及其时间等信息。

毁伤效果评估模型以各类机型数据库、全球机场数据库、弹目效能数据库为支撑，设计寻找最小起降窗口的算法，依此判断机场跑道针对某类机型是否成功封锁，同时对该算法的效率与精度进行评估，在确保效率的同时尽可能地提高精度，提高了该模型的实用性。

功能恢复时间评估模型以路面修复数据库为基础，对毁伤效果评估模型中的算法进行改动，对已封锁的机场跑道，可找到受毁伤最小的与最小起降窗口等大的矩形区域，结合路面修复数据库，可得到最快恢复该机场跑道起飞功能的方法和时间。

2 关键模型设计

本文仿真模型中最关键的部分为毁伤效果评估模型和功能恢复时间评估模型，前者对打击后机场进行毁伤效果评估，判断其是否被成功封锁；后者实现对被封锁机场的最短修复时间进行评估。

2.1 毁伤效果评估模型

绝大多数飞机起降都需要一块未受毁伤的矩形跑道区域，一般将某类机型起飞或降落所需的最小矩形区域称为该机型的最小起降窗口。机场跑道遭受攻击后，若仍存在最小起降窗口（竖直或倾斜皆可），则视为未成功封锁该跑道，反之则认为成功封锁该跑道，因此，如何判断打击后机场跑道是否仍存在最小起降窗口是判断是否封锁成功的关键，本节采用将最小起降窗口作为模板对整个跑道进行遍历的算法，并评估其效率与精度的关系。

2.1.1 算法设计

在给定机场跑道和最小起降窗口的长宽的条件下，可计算出机场跑道可能的最大倾斜角度，以机场跑道左上角为原点，跑道的宽为x轴，跑道的长为y轴构造直角坐标系如图2所示，令最小起降窗口的长边与y轴夹角∠ABE=α，当最小起降窗口逆时针旋转至图3所示角度时，α达到最大，令此最大值为β，此时应满足方程

实际上，还应满足 Lwcos α+Wwsin α≤Lr，即最小起降窗口不能超出机场跑道的上下边界，但由于一般Lr是Lw+Ww的几倍甚至十几倍，故可忽略此式。

由式（1）可解得

同理，最小起降窗口沿顺时针旋转到达夹角最大时也为β，令此时最小起降窗口的长边与y轴夹角为负，在-β≤α≤β的条件下，通过上下左右平移一个较小的距离遍历跑道来寻找最小起降窗口，将最小起降窗口的矩形视作一个模板，xA，yA表示A的横纵坐标，依此类推，令Δx和Δy表示搜索时横向和纵向平移的距离，那么算法如表1所示。

表1 最小起降窗口搜索算法

2.1.2 效率评估

通过每次旋转 Δα，遍历［-β，β］区间，可得到在此种精度（Δα，Δx，Δy）的搜索中的窗口数目。精度越高，Δα、Δx、Δy越小，找到最小起降窗口的可能性越大，找到的数目越多，但搜索效率也随之降低。如图3所示，横向平移最大距离Δxmax与α满足关系

同理，纵向平移最大距离Δymax与α满足关系

令完成整个搜索算法需要的总模板数为N，那么有

令判断每个模板是否存在弹坑的时间为TD，完成整个算法的时间即为t=N·TD。由上式可以看出，在Δα和Δy不变的前提下，时间t与Δx成反比；在Δα和Δx不变的前提下，时间t与Δy成反比；在Δx和Δy不变的前提下，情况较为复杂，随着Δα的减小，2β/Δα随之线性增大，但模板与y轴的夹角越小，此夹角下的模板数越少，因此，随着Δα的减小，越大。综上，在Δα1缩小为Δα2（Δα1=nΔα2），那么N2＞nN1，其中N1和N2分别对应在Δα1和Δα2精度下的总模板数。

2.2 功能恢复时间评估模型

若打击后机场跑道不存在某类机型的最小起降窗口，需要判断如何使用最短时间恢复最小起降窗口使该类机型顺利起飞，可通过对2.1.1节中α-最小起降窗口搜索算法略微改动实现功能恢复时间评估模型。

在每次判断模板中是否存在弹坑的同时，判断该模板中存在的弹坑数是否为当前最少，算法改动如下，令c记录当前已搜索模板中弹坑最少模板的弹坑数，D为跑道上总弹坑数如表2所示。

表2 最小起降窗口搜索算法（改）

可以看出，该算法完成后，会得到弹坑数最少的模板及其坐标信息，结合路面修复数据库，可得到最快恢复最小起降窗口的时间为c·T·S，T为通过查询数据库得到的该跑道路面单位面积的修复时间，S为弹坑面积。

3 模型仿真实验

本节首先对最小起降窗口搜索算法进行仿真实验，然后对算法效率与精度之间的关系进行评估。

3.1 最小起降窗口搜索算法

仿真条件为：机场跑道长为2 500 m，宽为40 m，某机型的最小起降窗口长为800 m，宽为20 m，生成弹坑分布如图5（a）所示。

在 Δα=0.5°，Δx=2 m，Δy=2 m 的精度条件下，执行最小起降窗口搜索算法，得到87个最小起降窗口，如图 5（b）所示。

图5（b）中虚线围起来的矩形区域中，取800m×20 m的任一区域都是最小起降窗口，图中给出其中一个最小起降窗口。（由于机场跑道长宽比例过大，因此，图 5（a）和图 5（b）中对比例进行压缩，以致最小起降窗口看起来不是矩形，但其在真实比例下为矩形）。

3.2 效率与精度的关系仿真

为评测效率与精度之间的关系，在不同精度条件下进行最小起降窗口搜索，针对每种精度进行10次仿真，取其时间平均值，若某型号子母弹携带子弹数为100发，结果如下页表3。

由表3可以看出，仿真实验的结果基本与2.1.2节的分析基本一致，在精度（Δx，Δy，Δα）=（0.05°，0.1 m，0.1 m）的条件下，判断时间已经达到481.23 s，超过8 min，实际中可根据具体情况的时间需求来选择精度，达到兼顾效率与精度的目的。

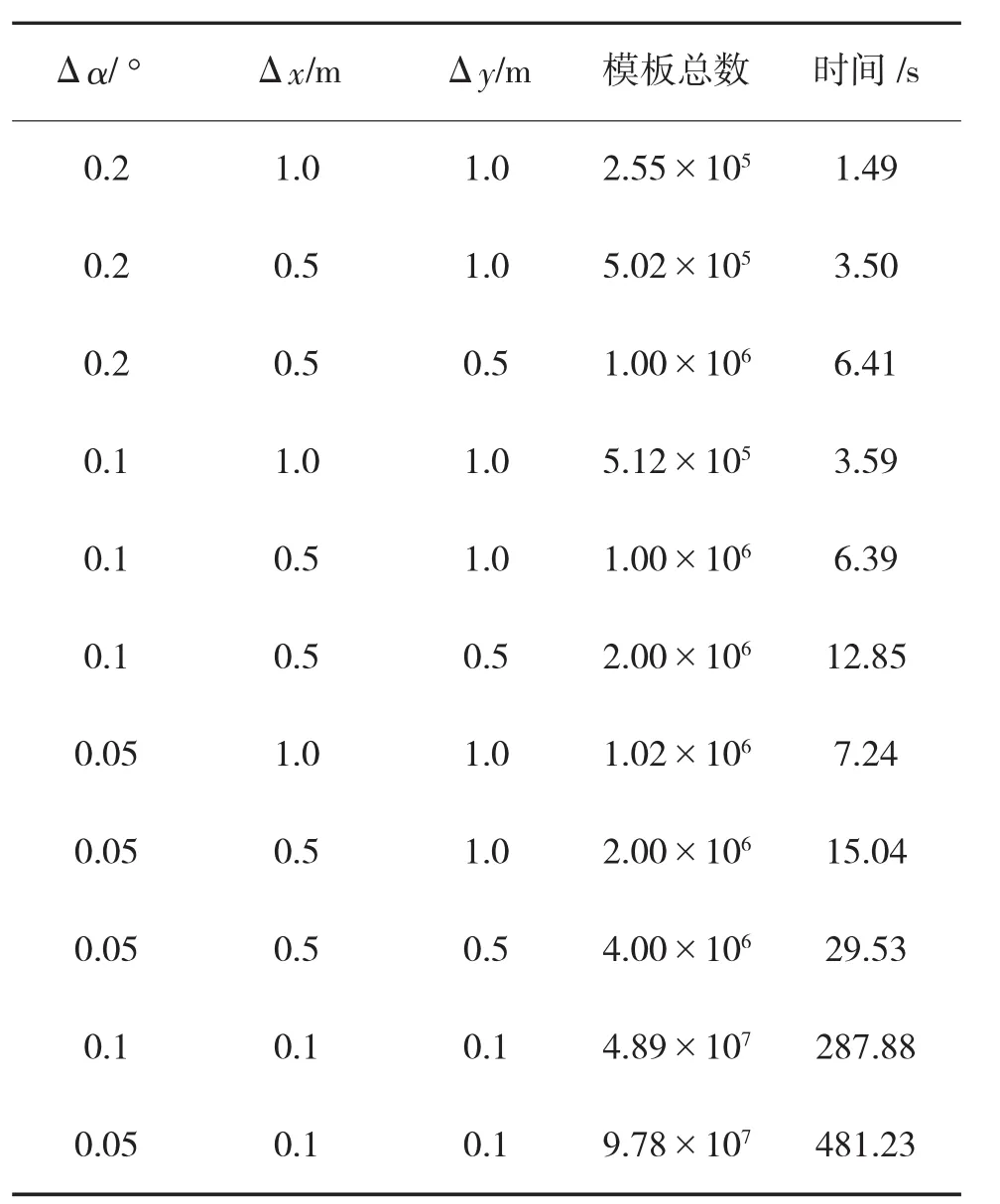
表3 效率与精度关系

4 结论

通过建立各类机型数据库、全球机场数据库、弹目效能数据库、路面修复数据库，设计毁伤效果评估模型和功能恢复时间评估模型，若敌方对我方机场跑道进行打击，可以首先使用毁伤效果评估模型检测，确定打击后机场跑道是否仍然存在最小起降窗口，使飞机正常起飞；若不存在，则可使用功能恢复时间评估模型计算最快恢复时间，在实战中具有重要意义，同时为下一步更完善的仿真模型建立提供基础。

［1］马波，周成平，娄联堂，等.基于图像分析的机场打击效果自动评估研究 ［J］.华中科技大学学报，2004，32（6）：13-15.

［2］蒲刚，许鹏，任平，等.基于图像分析的机场跑道毁伤效果评估研究［J］.舰船电子工程，2012，32（2）：31-32.

［3］苏高峰，王宝树，苗启广.机场跑道的打击效果评估研究［J］.火力与指挥控制，2008，33（11）：46-47.

［4］王卫星，周宁.遥感图像中机场跑道的检测［J］.重庆邮电大学学报，2010，22（1）：108-111.

［5］戴毅，苗育红，周江华.毁伤概率评估的加权蒙特卡罗方法［J］.计算机仿真，2008，25（3）：115-118.

［6］王帅，陈立云，袁曦，等.子母弹打击机场跑道毁伤概率的蒙特卡洛仿真［C］//系统仿真技术及其应用学术会议，2009.

［7］费智婷，周朝阳，岑小锋，等.机场跑道毁伤效果评估系统研究［J］.指挥控制与仿真，2012，34（1）：66-69.

［8］王刚，李臣明，刘怡昕.远程制导火箭子母弹对机场跑道毁伤研究［J］.火力与指挥控制，2015，40（4）：111-114.