纯角度信息的舰载无人机目标运动分析算法

张渝缘，刘 健，石章松

（海军工程大学，武汉 430033）

0 引言

舰载无人机（Unmanned Aerial Vehicle，UAV）系统作为无人飞行器与舰艇平台及其装备相结合的新事物，已成为一支功能日趋全面的作战力量，越来越受到各国军方的重视。相比于有人舰载机，舰载无人机具有轻便、灵活、更机动的特点，它的出现为海上作战提供了一种灵活、高效、低风险的战场感知和战斗应用平台［1］。通过舰载无人机，可实现对目标协同定位与跟踪，提高水面舰艇的远程感知能力。利用光电系统的目标运动分析处理系统，对舰载无人机光电系统测量的目标高低角、方位角，以及无人机自身平台的航向、速度、高度、机载GPS提供的经纬度等信息进行合理解算，实现对陆、海上目标的定位与跟踪。

基于角度信息的目标运动分析（BTMA）是指在不使用向外辐射能量的设备情况下，仅利用获取的目标角度信息对目标的运动状态参数（初始距离、速度、航向等）进行解算的过程。

本文提出了基于无人机观测目标的角度信息，构建目标运动分析模型，实现对目标快速有效定位，并求解相应的目标运动参数，结合具体的仿真算法，对目标运动进行仿真分析，验证了算法的有效性和可行性，为未来无人机目标定位研究提供参考。

1 基于角度信息的目标运动分析算法数学模型

在目标定位中，将无人机此时的坐标作为相对地理坐标系的原点，X轴指向东，Y轴指向北，Z轴垂直XY平面指向天顶［2-3］。

记 D1、Km、φm、Vm为目标初始距离、航向、俯冲角和速度，目标作匀速直线运动。无人机的航向为Kw、速度为 Vw、俯冲角为 φw。分别记 β1，β2，…βk；ε1，ε2，…εk为t1，t2，…tk时刻无人机测得的目标方位角和目标俯仰角。

（D1，Km，φm，Vm）能唯一确定目标的轨迹。所谓的目标定位，就是利用测量值（β1，β2，…，βk）和（ε1，ε2，…，εk）解出上述向量的过程。

根据相对运动的空间几何封闭性原理，从XYZ 3个方向分析，可以得到下面3个方程［4］：

对 j=0，1，…，k，εk，βk为已知量，利用式（2）可形成关于（Vmx，Vmy，Vmz，D1）的非线性方程组，如果能解出上述的4个参数，则可求出目标的初始距离、航向、俯冲角、速度，再根据无人机的航向和速度，便可以唯一地确定目标的运动轨迹。

2 可观测性分析

由式（2）知，方程组未知量为：Vwx，Vwy，Vwz，Dj，D1。可知该方程组不可解。为满足方程有唯一解的要求，采用构建 D1D2，D2D3两段方程［5］联立对目标求解。构成方程式如下：

未知量：Vwx，Vwy，Vwz，D1，D2，D3。此时方程组可有唯一解，写成矩阵形式得：

记式（4）的系数矩阵为F，讨论当无人机作匀速直线运动时的可观测性问题。

无人机速度在坐标系中3个分量Vwx，Vwy，Vwz为已知量，因其作匀速直线运动，有：，，，，由行列式性质易知：。

可以得出结论：当无人机作匀速直线运动时，目标运动状态是不可观测且不可解的。

下面讨论当无人机作匀加速直线运动时的可观测性。知：

经计算并化简得到：

3 算法原理

经过计算，将式（2）经过化简消去Dj，整理得到：

由于测量误差的存在，上式一般不严格满足，此时，可得下式：

经过k次观测，基于最小二乘估计原理，构建如下极小化目标函数：

为求得目标运动参数 Vmx、Vmy、Vmz和 D1，分别对其求偏导，并使：

对式（9）简化，令：

或

其中：

针对上面的算法分析，是在观测到的目标方位角 β1，β2，…，βk，俯冲角 ε1，ε2，…，εk未受到噪音污染的条件下进行的，解式（16）便可以求出Xk的最优解。假定目标方位、俯仰存在测量误差 δβj，δεj，j=0，1，…，k，求解目标参数 Xk，将 βj=βmj+δβj，εj=εmj+δεj带入到式（16），利用式（16）解出。符号 βmj，εmj代表目标方位、俯仰测量的精确值。记可得：

考虑到式（16）最小二乘估计若采用成批处理数据的方式，将导致算法的实时性差、所需存储空间大和计算复杂等缺点。此处选用递推最小二乘定位算法［6］进行解算。

解得：

利用矩阵反演公式化简得：

其中I为3阶单位矩阵，且由式（16）可知：

利用式（21）将式（22）化简得：

所以，利用上面推导得出的递推格式，便可唯一确定目标相对运动参数，根据求得的，可实现对目标航向km，俯冲角εm，速度Vm的运动参数的估计。同时根据初始距离，可求出对目标X，Y，Z方向实时距离 Dx，Dy，Dz，从而求出实时距离 D。即：

4 算法仿真及误差分析

4.1 对陆上目标的定位跟踪

假定无人机作匀加速直线运动，速度25 m/s，航向 80°，俯冲角 1°，加速度 0.07 m/s2，跟踪时长 300 s。目标作匀速直线运动，速度20 m/s，航向10°，目标俯冲角3°。无人机与目标初始距离为3 000 m，目标相对无人机初始方位角60°，俯仰角30°，角度测量误差均方差为0.05°。依据前述的解算方法进行40次仿真解算，求得目标相对无人机初距均值、初距相对误差、航向均值、航向绝对误差、俯冲角均值、俯冲角绝对误差、速度均值、速度相对误差曲线如图2～图9所示：

具体误差如下页表1所示。

由上图和表1可知，在测量误差为0.05°的情况下，观测300 s后，算法得到的参数结果与真实值较接近，初始距离和速度相对误差控制在5%以内，目标航向和目标俯冲角误差控制在2°以内，其精度可以接受。

4.2 对海上目标的定位跟踪

当对海上目标进行定位时，由式（3）可知，当无人机作匀速直线运动时，目标是可观测的。假定无人机作匀直线运动，速度 60 m/s，航向60°，俯冲角5°，跟踪时长40 s。目标作匀速直线运动，速度54m/s，航向30°。无人机与目标初始距离为4000m，目标相对无人机初始方位角30°，俯仰角30°，角度测量误差均方差为3°。依据前述的解算方法进行40次仿真解算，求得目标相对无人机初距均值、初距相对误差、航向均值、航向绝对误差、俯冲角均值、俯冲角绝对误差、速度均值、速度相对误差曲线如图10～图15所示：

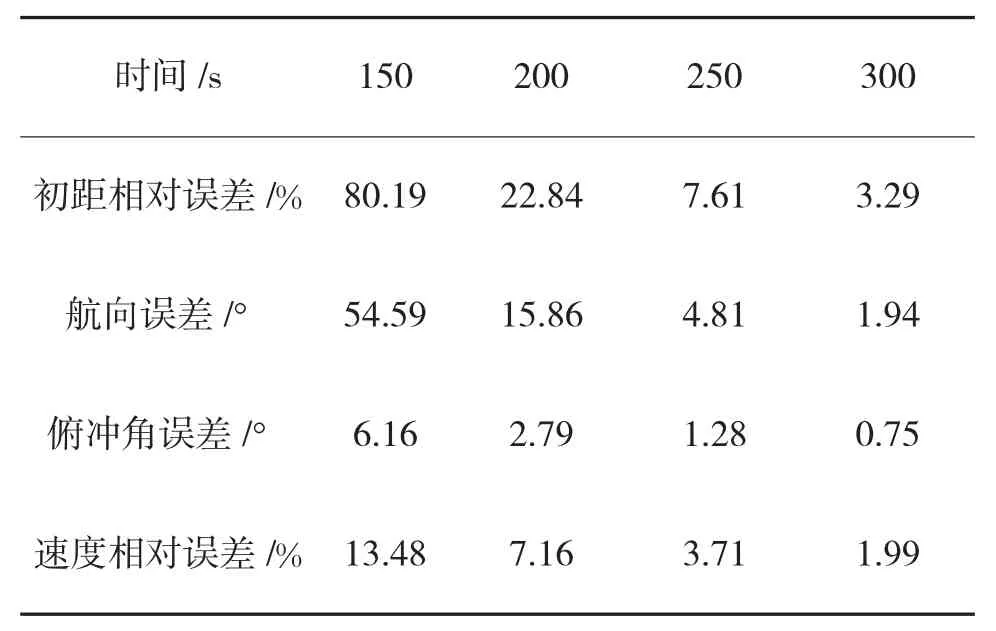
表1 误差统计表

不同测量误差条件下误差如表2所示。

由上图和表2可知，在测量误差为1°和3°的情况下，观测100 s后，算法得到的参数结果与真实值较接近，初始距离和速度相对误差控制在5%以内，目标航向误差控制在0.5°以内，当误差不断增大时，初始距离和速度误差明显升高。

通过此算法，可以对二维和三维空间目标进行跟踪定位。其计算精度较高，收敛速度较快，在实际中具有一定应用价值。

表2 误差统计表

5 结论

为通过舰载无人机对陆、海上目标定位跟踪，本文建立目标运动模型，并根据目标运动特性，构建等式，利用最小二乘法，对目标角度信息解算，求得目标初始距离、航向及速度，以便对其进行定位跟踪，并通过仿真验证，对计算信息进行误差分析。由于目标都是近距离直线运动，算法局限性较大，对远距离慢速机动目标的定位分析还有待深入研究。

［1］黄定超，樊兴，郭铭.舰载无人机系统技术研究［J］.舰船电子工程，2008，167（5）：32-36.

［2］李晨，韩崇昭.纯方位跟踪问题研究及算法性能［J］.火力与指挥控制，2007，32（7）：4-7.

［3］王航宇，卢发兴，刘健.大噪声背景下的纯方位导引方法［J］.火力与指挥控制，2001，26（4）：77-80.

［4］曲毅，刘忠，郭睿，等.基于光电观测信息的空中机动平台被动跟踪研究［J］. 系统工程与电子技术，2009，31（5）：1093-1096.

［5］孙亮，于雷，王凯，等.机载三维纯方位无源定位的可观测性［J］.空军工程大学学报，2008，9（4）：1-5.

［6］莫成坤，陈树新，吴昊，等.基于角度信息的递推最小二乘无源定位算法 ［J］. 计算机测量与控制，2014，22（9）：2863-2866.

［7］贺若飞，李大健，刘宏娟，等.无人机自主控制应用需求及研究发展分析［J］.火力与指挥控制，2016，41（5）：1-5.

［8］丛红日，周海亮，陈邓安.舰载反潜直升机蛇形机动前方护航搜索方法及其仿真［J］.兵器装备工程学报，2016（6）：158-161.