“拍照赚钱”的任务定价

卢施奇，陈子炜，程 荃

(北京体育大学 管理学院，北京 100084)

1 问题重述

1.1 背景知识

“拍照赚钱”是随着互联网的发展新兴起的一种自助式服务模式。用户在手机上下载App，注册成为会员，然后从App上领取需要拍照的任务，赚取App对任务所标定的酬金。这种基于移动互联网的自助式劳务众包平台，为企业提供信息搜集和商业检查，相比传统的市场调查方式可以大大节省调查成本，并且有效保证了数据调查的真实性，缩短了调查的周期。因此App成为该平台运行的核心。任务定价是App的核心要素，因为如果定价不合理，有的任务就会无人问津，最终导致商品检查的失败。

1.2 要解决的问题

研究给出的部分项目的任务定价规律，并分析任务未完成的原因。

给这些项目设计新的任务定价方案，并和原方案进行比较。

实际情况下，多个任务可能因为位置比较集中，导致用户会争相选择，一种考虑是将这些任务联合在一起打包发布。在这种考虑下，如何修改前面的定价模型，并分析对最终的任务完成情况的影响。

对给处的新项目设计一个任务定价方案，并评价该方案的实施效果。

2 问题分析

问题一：首先，笔者认为任务的定价是一个二元函数，它和任务地点距离任务中心点的距离有关，也和会员地点距离会员中心点的距离有关。笔者先用Matlab对任务地点进行层次聚类，结果显示最好分成几类，然后运用SPSS的K均值聚类得出这几类的坐标。在谷歌地图上对这几个坐标一一查询，确定出中心区域(会员地点同理)。其次，用Excel建立函数求出各个任务地点与中心点的距离以及各个会员地点据会员中心点的距离，然后利用这些距离数据拟合出一个关于任务价格的函数，并且测定该函数与原数据的拟合度。最后，分析任务地点与任务聚集的中心区域和会员聚集地三者关系，并运用目标设定理论等心理学理论分析任务定价的规律和任务未完成的原因。

问题二：在问题一的基础上，将任务获取的难易程度纳入考虑范围，并且将人均获取的任务量定义为任务获取难易的程度。

问题三：因为是涉及任务联合问题，因而将原来的定价模型分为两个部分，第一部分即用户到该任务点所应获得的酬劳，以及从该任务点出发到其他联合任务点所需要的酬劳。由此酬劳的其中一部分即需要考虑用户同第一个任务点的距离及其相关因素，第二部分即任务点之间转换所需考虑的因素。修改后的模型可以促进任务的完成率，提升部分用户的经济收入。

问题四：提高计算精度，将会员应得的报酬更加细致地表现出来。从App的收入以及客户满意程度这两个维度对新的任务定价方案进行分析。

3 模型假设

第一，假设所有人都是理性的经济人。

第二，假设某些个别的任务位置偏离，导致个别任务中心区域存在误差。

第三，假设会员选取任务的考虑因素只是客观的，不考虑多样的主观因素。

第四，假设会员之间不存在差异性。

4 符号说明

本文所用主要符号变量符号及意义如表1所示。

表1 文中主要变量符号说明

续表

5 模型建立和求解

用Matlab对任务地点进行分层聚类，结果显示最好分成五类。所以，附录一中的任务地点可以被分为类别1、类别2、类别3、类别4、类别5。各个类别所包含的任务地点数量如表2所示。

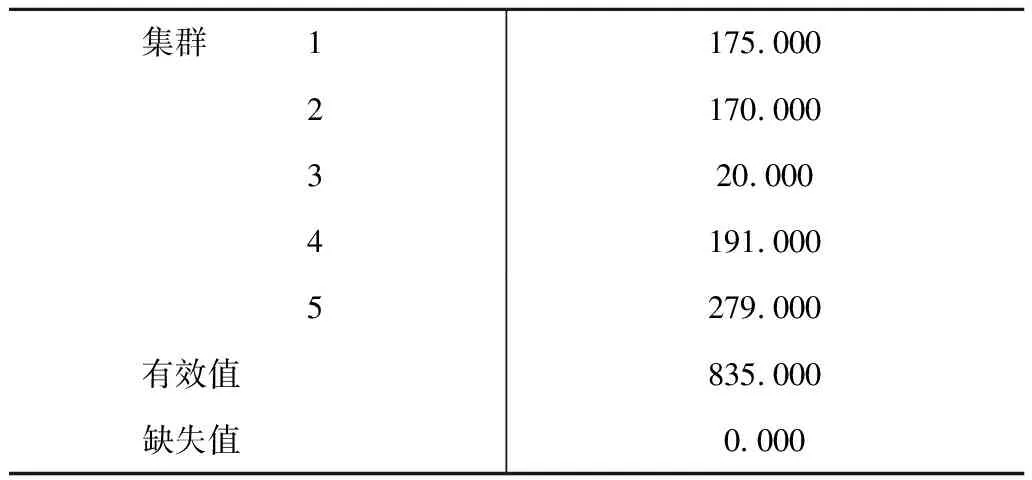
表2 每个集群中的频数分布

之后再利用SPSS软件中的K均值聚类，在5个类别中分别得到5个中心点。坐标分别为：

(X1=22.943214445,Y1=113.75312006)、(X2=23.00649466，Y2=113.10047901)、(X3=23.58329231，Y3=113.59590074)、(X4=22.66128623，Y4=114.0856776)、(X5=23.16947939，Y5=113.31220156)如表3所示。

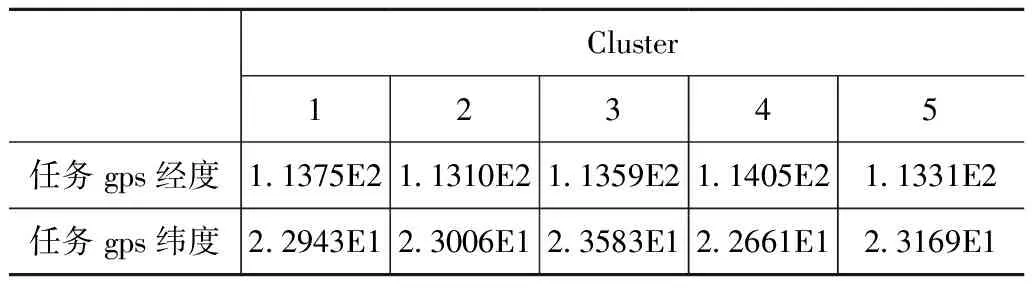
表3 最终聚类中心

然后用Excel软件将附件一中的任务位置、任务执行情况以及上文提及的5个中心点显示在三维地图上。

在Google地图上对这五个坐标一一查询，也确定出了这五个中心区域。然后用Excel将附件一中的任务位置和附件二中的会员位置显示在了三维地图上，分析任务地点与会员位置的关系。

对会员所在地的经纬度进行K均值聚类，发现其仅有一个中心点(Cx=22.92932908，Cy=113.63726825)。

之后笔者运用以下函数计算各个类别中各个任务地点距离中心点的距离Dn，以及各个会员地点距离会员中心点的距离Dc。

Dn=6371004×ACOS(SIN(RADIANS(Xn))×SIN(RADIANS(xn))+COS(RADIANS(Xn))×COS(RADIANS(xn))×COS(RADIANS(yn-Yn)))

Dc=6371004×ACOS((SIN(RADIANS(Cx))×SIN(RADIANS(xn))+COS(RADIANS(Cx))×COS(RADIANS(xn))×COS(RADIANS(yn-Cy))))

最后，运用SPSS数据分析，得出了任务价格Z与Dn，Dc呈现下图的函数关系：

Z=0.31225337×Dn+0.16950474×Dc+64.71688731

笔者得出的价格曲线，与原数据拟合度达到了0.132。如表4所示。

表4 模型总结b

注：a.人地距离

b.任务标价

6 模型评论与推广

6.1 模型的优点

(1) 运用Matlab、SPSS等软件工具将附件中大量的数据聚类分析，结论更为清晰、直观。

(2)方案较为符合实际情况，具有可采纳性。

6.2 模型的缺点

(1)未考虑会员的主观因素及个体差异，所以计算结果与实际状况存在偏差，不够精确。

(2)近似处理对于计算的准确度存在影响。

(3)拟合优化程度是约为21%，也就是说，只能预测出约21%的价格，存在局限性。

[1]孙吉贵,刘杰,赵连宇. 聚类算法研究[J]. 软件学报,2008(1):48-61.

[2]王惠文,孟洁. 多元线性回归的预测建模方法[J]. 北京航空航天大学学报,2007(4):500-504.

[3]陈希孺. 广义线性模型(一)[J]. 数理统计与管理,2002(5):54-61.

[4]孙健敏. 人力资源管理中工作设计的四种不同趋向[J]. 首都经济贸易大学学报,2002(1):58-62.

[5]孙泠. 互联网+赋予大数据无尽想象[J]. IT经理世界,2015(15):18-20.