我国城乡恩格尔系数与居民收入的关系研究

毕宁远，邢天天

(1.浙江省春晖中学，浙江 绍兴 312000；2.清华大学 社会科学学院，北京 100084)

1 概 述

恩格尔系数是指食品支出占家庭支出的比重，其反映的是居民生活水平的高低。越富裕的家庭，食品支出占比越低。联合国粮农组织恩格尔系数的划分标准：59%以上为绝对贫困；50%～59%为温饱；40%～49%为小康；30%～39%为富裕；30%以下为最富裕。从我国总体来看，近几年恩格尔系数一直在下降，从2013年的31.2%下降到2014年的31%，2016年进一步下降到30.1%。与此同时，我国的居民人均收入则在不断攀升。一个国家的恩格尔系数必然与其相应的人均居民收入存在一定的关系，一般来说，居民人均收入越高，恩格尔系数越低。但是，对于城市地区和农村地区分别而言，由于产业结构和经济政策等的不同，不同地区的恩格尔系数与居民人均收入的关系鲜有学者讨论和研究。考虑到城市地区和农村地区的经济发展水平差距，恩格尔系数与居民人均收入的关系可能存在差异。我们认为，恩格尔系数与人均收入之间存在某种关系，这种关系可能是线性的，也有可能是非线性的。对于城市和农村地区而言，这种关系很可能是不同的。因此，我们将探究这种关系，分别建立起相应的回归模型，进而对城乡收入水平的差距现状做出分析。

本文结构如下：首先，我们通过对城市和农村2008—2015年的恩格尔系数和居民人均收入的数据散点图分析，发现二者的关系在城市地区和农村地区具有比较明显的不同趋势。因此我们分别针对城市、农村地区建立了恩格尔系数和居民收入的回归模型，结合回归统计R方的检验，通过比较多种类型拟合方程，发现采用线性回归模型更加准确简洁。此外，我们还对该线性回归方程进行了回归统计和方差分析，基于数值分析给出了两个模型的评价，即统计检验和显著性评估。并且基于所得到的两个回归方程，对城市、农村恩格尔系数—居民收入差异进行了讨论分析。最后给出了全文总结，指出了本文工作的亮度和不足。

2 城乡恩格尔系数与居民收入的回归模型

我们选取了中国国家统计局的公开数据，统计了自2008年至2015年我国城市和农村居民家庭的恩格尔系数以及居民人均收入资料，整理如图1所示。

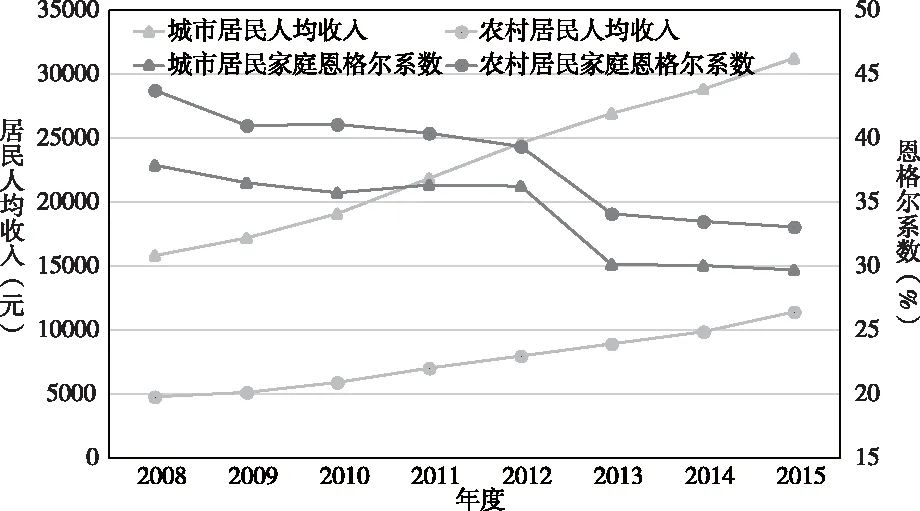
图1 2008年至2015年我国城镇和农村居民数据

结合该数据,我们可以发现城市或农村的居民的恩格尔系数与人均收入具有比较明显的负相关趋势。人均收入逐年依次上升，恩格尔系数逐渐下降。值得注意的是，恩格尔系数的提高，其主要因素则是人均收入、食品价格等。为简化处理，这里我们不讨论食品价格等因素对恩格尔系数的影响，只考虑恩格尔系数与人均收入的关系。因此，这里取居民人均收入为自变量X，恩格尔系数为因变量Y，分别绘制城市和农村相应的散点图，如图2所示。

图2 城乡恩格尔系数与居民人均收入散点分布

观察图2，城市居民和农村居民的散点分布明显存在不同的趋势，其分别的恩格尔系数与人均收入之间存在一种近似线性关系，随着人均收入的提高，二者的恩格尔系数都在下降，但城市的下降趋势趋于平缓，而农村的恩格尔系数下降非常急剧。因此，结合城市和农村的散点趋势明显不同，我们认为非常有必要将二者分开讨论，即分别进行回归分析。

下面采用最小二乘法对模型进行估计,建立Y与X的回归模型：城市/农村恩格尔系数—收入模型，以下简称“城市/农村恩—收模型”。分别采用指数、线性、对数、二次多项式、幂函数关系作为回归拟合方程，如表1和表2所示。

上述所列拟合方程的结果并不都是非常切合的，一个好的回归方程将使得人们对变量之间的本质关系有着更加深刻的理解。因此，选取一个好的回归方程将是非常重要而且关键的一步。决定系数是衡量一个回归方程优劣的标准之一，为检验模型的优劣，我们考虑其相应的决定系数(R2)。R2描述了回归模型所解释的因变量方差在总方差中的比例。其表达式为:

表1 “城市恩—收模型”的回归方程及检验

表2 “农村恩—收模型”的回归方程及检验

结合表1和表2，我们发现在“城市恩—收模型”回归中，二次多项式的决定系数最高，线性方程次之。而对于农村而言，同样也是线性方程和二次多项式的决定系数排在前列，鉴于此，另外考虑到回归方程的简洁性和使用方便性，我们一并采用线性拟合的结果作为回归方程。即，“城市恩—收模型”回归为y= -1458.4x+ 72837(R2=0.8072)，“农村恩—收模型”回归为y= -543.07x+ 28396(R2=0.8981)。

3 城乡恩格尔系数与居民收入的回归分析

上述选取模型过程中，只是简单选取了R2作为参考依据，为了进一步评价所选取的两个线性回归方程，下面我们将对两者进行详细的回归分析。首先，通过采用数学软件，分别对两组数据进行回归统计，统计结果如表3所示。

表3 回归统计

为了判定回归模型的回归效果，还需要对上述模型进行方差分析，通过数学软件进行数值分析可以得到表4。

表4 方差分析

这里主要关注回归分析中的显著性统计F的值，以统计常用的0.05显著水平为例，这里的0.002423和0.000344均明显小于0.05，则F检验通过，因此上述两个整体回归方程都显著有效。

通过统计检验和显著性评估以后，我们再对两个可适用的回归方程进行讨论，主要有以下两点发现。

(1)“农村恩—收模型”的线性回归方程斜率绝对值明显比“城市恩—收模型”的要大，意味着随着人均收入的提高，农村的恩格尔系数将比城市下降得更为迅速。同样地，意味着尽管随着恩格尔系数的共同下降，城市居民和农村居民的人均收入差距可能存在进一步拉大。

(2)在上述的两个回归方程中，“农村恩—收模型”的关系趋势比“城市恩—收模型”更加明显。主要原因可能是，城市的恩格尔系数受到更加多的影响因素的干扰，比如教育医疗产业的结构变化，劳动力和生产效率的改变等对其影响较大，人均收入的影响不再那么明显。另一种可能的原因是上述建立的线性回归方程具有一定的局限性，也就是说，该线性回归方程仅在居民人均收入不足够高的条件下具有可靠性，当人均收入足够高时，恩格尔系数对居民生活质量的评定不再直接，例如，当人们收入非常高时，人们对食物的品位和要求也在提高，甚至有人愿意掏出大笔支出用于美食开支，因此此时恩格尔系数可能下降趋势不再明显。

4 结 论

综上所述，基于2008—2015年我国城镇和农村居民家庭的恩格尔系数，以及居民人均可支配收入数据资料，我们最终将“城市恩—收模型”回归为y=-1458.4x+72837(R2=0.8072)，“农村恩—收模型”回归为y=-543.07x+28396(R2=0.8981)。同时，我们对两个模型分别进行了统计检验和显著性评估，其显著性统计F的值分别为0.002423和0.000344，证明了两个整体回归方程都显著有效。该两个线性回归方程形式简洁，对自变量和因变量的关系描述准确，显著且可靠，可以被推广使用。同时该两个方程对乡恩格尔系数与居民收入的关系预测和分析具有很大意义。但是，由于本文选取的数据量有限，样本数仅为8，故回归的结果可能具有一定的局限性。

[1] 汪建萍.中国城乡居民恩格尔系数分析 [J].统计与决策，2002(4)：32-33.

[2]赖文燕.运用恩格尔系数分析我国城乡居民生活差异 [J].北方经济：综合版，2010(6)：26-27.

[3]顾剑华.黄河流域城乡恩格尔系数对经济增长的动态效应与地区差异[J].商业时代，2010(4)：120-121.

[4]张鸿武，王亚雄.恩格尔系数的适用性与居民生活水平评价[J].统计与信息论坛，2005，20(1)：20-23.