中国工业低碳全要素生产率的测算及分解

2018-03-01许冬兰张敏

青岛科技大学学报(社会科学版) 2018年4期

关键词：工业

许冬兰张敏

[摘要]采用動态EBM-MI指数模型测度2000—2015年中国33个工业行业的低碳全要素生产率，并将低碳全要素生产率分解为规模效率变动（SEC）、动态进步（DPC）、纯技术进步（TPC）、纯技术效率变动（PTEC）以及环境效率变动（EC）五项。研究结果表明：1.中国工业低碳全要素生产率的年均增长率为4.3%，其历年指数大都围绕1波动。在五个分解项中，技术进步对低碳全要素生产率增长发挥的作用最大。2.绝大多数工业行业的低碳全要素生产率是增长的，且增速具有较为明显的行业异质性，技术密集型、清洁型工业的增速明显高于其他行业，污染密集型工业的增速最为缓慢。

[关键词]低碳全要素生产率;工业;动态EBM-MI指数模型

[中图分类号]F42[文献标识码]A [文章编号]1671-8372（2018）04-0019-06

The measurement and decomposition of Chinas industrial low-carbon total factor productivity

—based on the dynamic EBM-MI index model

XU Dong-lan， ZHANG Min

（Economics College， Ocean University of China， Qingdao 266100， China）

Abstract：The dynamic EBM-MI index model is used to measure the total factor productivity of low-carbon in 33 industrial sectors in China from 2000 to 2015， which has been decomposed into five indices， including scale efficiency change （SEC）， dynamic progress （DPC）， pure technological progress （TPC）， pure technical efficiency change （PTEC） and environmental efficiency change （EC）. The results show that Chinas industrial low-carbon total factor productivity has an average annual growth rate of 4.3%， and its index is mostly fluctuated around 1 over the years. Among the five decompositions， the technological progress plays the largest role in the growth of low-carbon total factor productivity. It is also found that the total factor productivity of low-carbon in most industrial sectors is increasing， and the growth rate has obvious industrial heterogeneity. The growth rate of technology-intensive and clean industries is significantly higher than that of other industries， and the growth rate of pollution-intensive industries is the slowest.

Key words：low carbon total factor productivity; industry; dynamic EBM-MI index model

The measurement and decomposition of Chinas industrial low-carbon total factor productivity

—based on the dynamic EBM-MI index model

XU Dong-lan， ZHANG Min

（Economics College， Ocean University of China， Qingdao 266100， China）

Key words：low carbon total factor productivity; industry; dynamic EBM-MI index model

一、引言

伴随着全球气候变暖和《联合国气候变化框架公约》的制定，能源消耗与科学发展等问题越来越受到国际社会的关注，“低碳经济”“低碳发展”等新型理念也愈发得到人们的认同。长久以来，如何实现经济与环境的协调发展一直都是学术界关注的热点，且中国现阶段处在经济转型发展的关键时期，正面临着前所未有的能源和碳排放的双重压力。作为一种剔除了碳排放环境成本之后的全要素生产率改进，低碳全要素生產率将能源消耗和碳排放纳入到经济增长的核算框架当中，因而对其进行科学准确地测算必将有助于经济发展质量与综合效益的客观评价，且对于中国工业的低碳转型发展意义重大。

关于全要素生产率的核算，国外学者提出了诸多方法，其中应用最多的有代数指数法（AIN）、索洛余值法、随机前沿分析法（SFA）以及数据包络分析法（DEA）四种。Abramvitz在1956年提出了代数指数法（AIN），其核心思想是用产出指数与所有投入要素加权指数的比率来表示全要素生产率。该方法严格假定边际生产率不变和资本劳动完全替代，明显缺乏合理性，故并不适用于实证经济的研究[1]。Solow提出了索洛余值法，其基本思路是利用C-D函数计算出的产出增长率减去全部投入要素增长率后的残差来衡量全要素生产率的增长。该方法存在许多缺陷，比如它假设经济是完全竞争的，且技术效率完全有效，这些假设均不符合现实情况。随机前沿分析方法（SFA）虽不存在前面两种方法的缺陷，但它只适用于单产出、多投入的生产方式，无法对含有非合意产出的情况进行测算[2]。Farrel提出了数据包络分析法（DEA），克服了SFA的局限，可以用于研究多产出、多投入的生产类型，且无须给出具体的生产函数[3]。随后，Charnes等、Banker等分别提出了CCR模型和BBC模型，扩展了DEA在生产率测算方面的适用范围[4-5]，此两种模型的方向性距离函数主要是基于径向角度的DEA计算得出，并不适用于投入过度或者产出不足的情况。为解决该问题，Fare等提出了基于松弛向量的非径向、非角度的SBM方向性距离函数[6]。此外，为了考察全要素生产率的变动情况，学术界还构建了基于DEA的一系列生产率指数。Malmquist首次提出了缩放因子的概念;Caves等将其应用于生产率领域的研究，定义了Malmquist生产率指数[7-8]。Chambers等提出了具有相加结构且无须选择测度角度的Luenberger生产率指数;Chung等对Malmquist生产率指数进行扩展，得到了考虑环境因素的ML指数[9-10]。

由于前文所提到的全要素生产率测算方法均没有充分考虑资源、环境等因素的约束，故难免会对经济社会发展的综合绩效评价产生扭曲，进而不利于政策建议的制定。20世纪80年代以后，许多学者开始将环境因素引入到全要素生产率的框架中，使得全要素生产率的度量更加客观，也更加具有现实研究意义。在测算包含环境因素的工业全要素生产率时，一些学者进行了分区域、省份的分析和比较。涂正革将SO2排放量作为非期望产出，利用方向性环境距离函数测算了我国各地区的环境技术效率。研究发现，东部沿海地区的环境技术效率均较高，而中西部地区则普遍偏低[11]。吴军以工业废水中的COD和废气中的SO2作为“坏”产出，利用Malmquist-Luenberger指数对中国东部、中部及西部地区的全要素生产率分别进行了测算和比较[12]。汪克亮等将CO2、SO2作为“坏”产出，利用投入导向的BC2-DEA模型测算了2000—2007年中国省际全要素能源效率。结果表明，中国整体的全要素能源效率较低，且三大地区及各省份之间均存在显著差异[13]。屈小娥和席瑶用SO2、烟尘、粉尘、废水及固体废弃物五种工业主要污染物的排放量构造了环境污染指数，以其作为“坏”产出指标测算了1996—2009年中国28个省份的全要素生产率。并且将全要素生产率指数分解成技术进步指数和技术效率指数，又进一步将后者分解成为规模效率指数和纯技术效率指数[14]。

另外，部分学者着重研究了环境约束下中国工业分行业的全要素生产率。岳书敬和刘富华利用三种不同的模型，测算了考虑环境因素的2001—2006年中国36个工业行业的增长效率。研究发现，各行业间的经济增长效率差距显著，其中通信设备计算机及其他电子设备制造业、仪器仪表及文化办公用机械制造业的增速较快[15]。陈诗一估算了1980—2008年中国38个工业行业的绿色全要素生产率，发现考虑环境因素的全要素生产率比传统不考虑环境因素的低了很多[15]，这与Jeon和Sickles等许多研究的结论一致。他还指出，政府所实施的节能减排政策有效推动了工业绿色全要素生产率的改善，并且导致重工业的生产效率超过了轻工业[16]。李涛等基于双重产出RAM模型和SML指数，构建了中国低碳TFP指数，基于该指数考察了技术存量效应与效率追赶效应[17]。周五七和聂鸣将CO2排放作为非期望产出，测度了1998—2010年中国36个工业行业的绿色全要素生产率的动态变化，并且探究了资本深化、FDI等行业特征因素对于绿色TFP的增长影响[18]。邓晓兰和鄢哲明测算了2001—2011年中国36个工业行业的低碳生产率，检验了资源错配对于低碳生产率的影响。其结果显示，资源错配程度的加深确实阻碍了中国工业低碳生产效率的提高[19]。

本文利用数据包络分析法（DEA）理论框架中较为前沿的Epsilon-Based Measure（EBM）模型对中国工业行业的低碳全要素生产率进行评价。该模型是对传统DEA理论的重大突破，吸收了径向模型（CCR、BCC等）和非径向模型（以SBM模型为代表）的优点，在决策单元相对效率的评价上更具优势，评价结果更为客观可靠[20-21]。还参考雷明等的做法，引入动态要素，构建动态EBM-MI指数模型对中国工业行业的低碳全要素生产率进行测算[22]，分别从纵向时间序列和横向行业角度对测算结果进行分析，并据此提出相应的政策建议。

二、研究方法

（一）考虑环境约束的生产可能性集

本文将每个工业行业视为一个生产决策单元来构造生产前沿面，且分别用x、y、d表示投入要素、期望产出和非期望产出。假设每个行业使用m种投入要素，则，生产出r种期望产出，则，生产出s种非期望产出，则，那么生产可能性集P（x）可以表示为：

可以生产（1）

令第k个行业在第t期的投入和产出值为，且满足自由可处置、副产品和产出弱可处置性三公理。那么运用数据包络分析法（DEA）可将（1）式进行模型化变换为：

（2）

其中，表示各横截面观察值的权重，这一约束条件意味着生产技术为可变规模报酬（VRS）;若去掉该约束条件，则表示规模报酬不变（CRS）。

（二）考虑非期望产出的EBM模型

为了克服传统的DEA模型和方向距离函数（SBM）模型的弊端，Tone和Tsutsui提出了EBM模型，由此实现了径向与非径向两种方法的有效结合，放宽了径向函数投入要素同比例缩减的假定，综合了非径向函数考虑松弛变量的特点[23]，故能够对研究对象的效率进行更加精确有效的评价。

对于含有m种投入要素，z种产出的n个决策单元，考虑非期望产出的EBM模型可以表示为：

（3）

其中，表示EBM模型测度的最优效率得分，若= 1，表明该决策单元技术有效;表示径向部分的规划参数（由CCR模型计算得出）;为决策单元的线性组合系数;为非径向部分的投入要素松弛变量;表示含有径向和非径向松弛的核心参数，表示各项投入指标的相对重要程度（满足），二者得分由数据本身的客观属性决定;表示决策单元的第个非期望产出;、分别表示第t种期望产出的松弛改进部分的值和重要程度指标;、分别表示第s种非期望产出的松弛改进部分的值和重要程度指标;表示投入矩阵，表示产出矩阵，且。

（三）动态EBM-MI指数

将动态要素（一种当期产出作为下期投入的特殊要素）引入到考虑非期望产出的Malmquist模型当中，构建一个全新的动态EBM-MI指数，探究中国33个工业行业低碳全要素生产率的动态效应。

首先，生产前沿面的构造、投入要素、期望产出及非期望产出均同上文所述一致。假定为动态要素，则每个生产决策单元期的投入产出值可以表示为。

然后，运用考虑环境负产出的动态EBM-MI指数来测算中国各工业行业的低碳全要素生产率，且期到期的动态Malmquist指数的具体表达式如下：

（4）

（4）式中，动态Malmquist指数被进一步分解，即对技术效率指数中的规模效应实行了剥离，但未考虑到技术进步指数中也包含有相当部分的规模效应因素。为提升以上模型的科学性和解释能力，本文借鉴吕蕴虹的做法，将动态LCTFP分解为规模效率变动指数（SEC）、技术效率变动指数（TEC）和技术进步指数（TC），即[24]。

此外，技术效率变动指数（TEC）可被进一步分解为环境效率变动指数（EC）（反映环境质量效率的改善情况）和纯技术效率变动指数（PTEC）（反映管理水平及制度创新的情况），即;技术进步指数（TC）也可被进一步分解为动态进步指数（DPC）（反映动态要素的跨期生产影响效应）和纯技术进步指数（TPC）（反映投入要素的质量进步情况），即。

三、指标体系构建与数据说明

（一）指标选择

1.投入指标。（1）劳动投入。采用2000—2015年各工业行业全部从业人员的年末人数（单位：万人）进行衡量，具体数据来源于历年《中国工业统计年鉴》和《中国劳动统计年鉴》。（2）能源投入。选取以用标准煤法折算后的能源消费量（单位：万吨标准煤）作为代理指标，其数据来源于2001—2016年《中国能源统计年鉴》。

2.产出指标。（1）期望产出。采用2000—2015年各工业行业的增加值（单位：亿元）进行表征，为消除通货膨胀的影响，以2000年为基期，利用GDP平减指数对数据进行调整，数据来源是历年《中国统计年鉴》。（2）非期望产出。采用各工业行业的CO2排放量（单位：万吨）进行衡量，个体排放数据根据IPCC提供的方法计算得到。

3.动态要素。考虑到动态要素在生产过程中具有跨期影响的特征，而固定资产投资又恰好具有一定的收益滞后性和延续性，故本文采用固定资产投资作为动态要素进行衡量，其数据来源于2000—2015年《中国固定资产投资统计年鉴》。

（二）數据调整说明

为了保证前后分析的一致性，本文依据上文测算GVC嵌入程度指数的行业分类对以上年鉴中的数据按照行业进行了对应的合并加总处理。此外，由于工业能源消费量与CO2排放是按照全部工业企业核算的，而其他要素是按照规模以上工业企业进行统计的，为保证所有投入产出统计口径的一致性，本文参考陈诗一的做法，将行业投入产出数据由规模以上工业企业口径统一调整至全部工业企业口径[25]。

四、测算结果分析

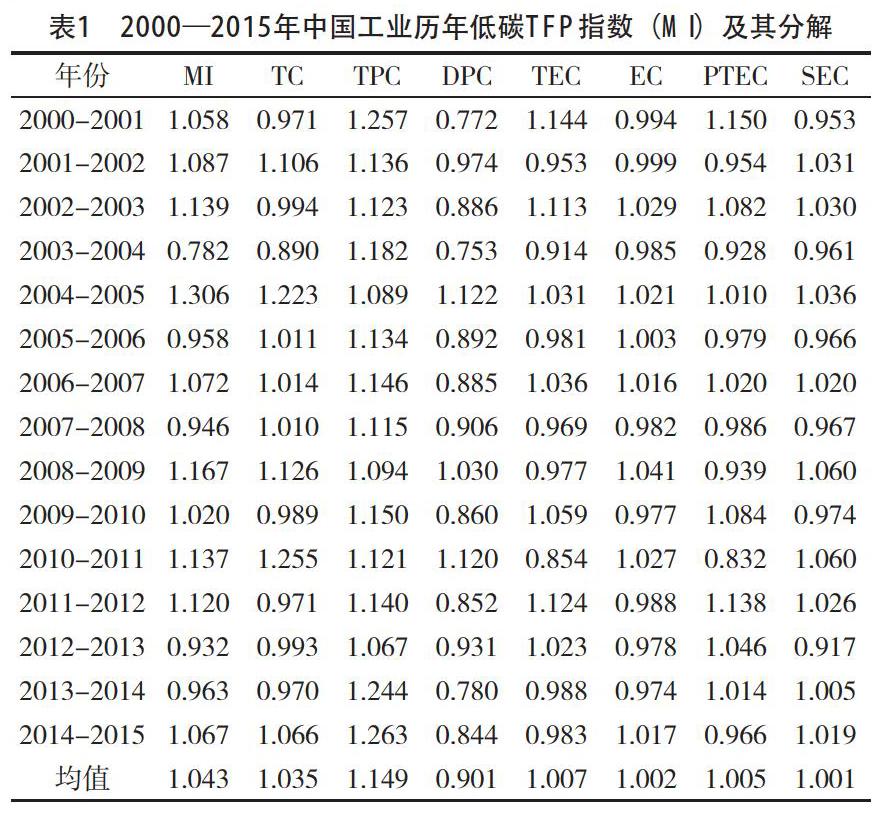
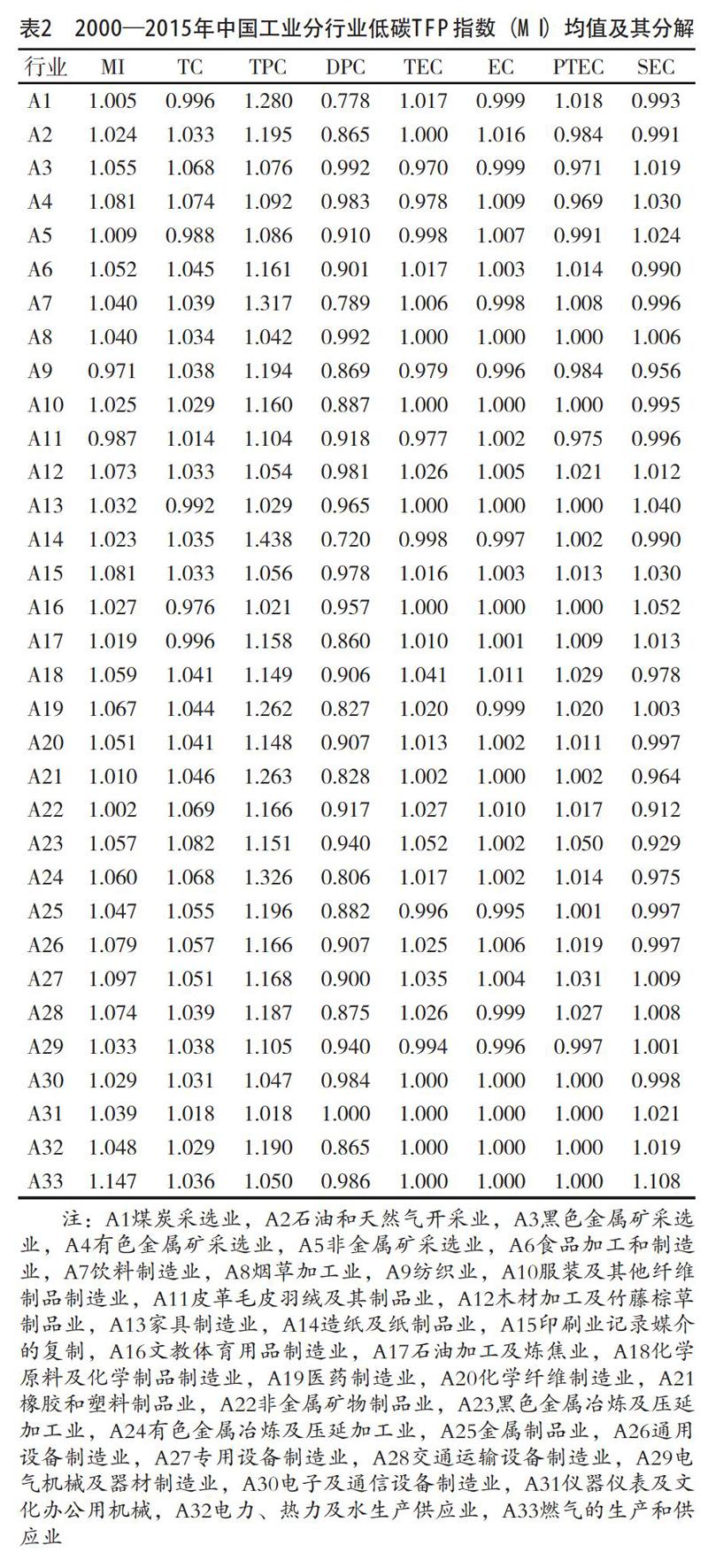
本文利用MaxDea 6.4专业版软件测算了中国工业行业的低碳全要素生产率指数及其分解项（见表1、表2）。

从表1可以看出，2000—2015年中国工业低碳全要素生产率指数（MI）的平均值为1.043，低碳全要素生产率的年均增长率为4.3%，并且历年指数基本围绕着1而小幅波动。具体来讲，2000—2003年持续增长，随后迅速降低，且在2004年降至最低后出现反弹，并于2005年达到峰值1.306;2005—2012年指数大致呈现“锯齿形”走势;2012年后再次上升。2000—2012年大多数年份的低碳TFP指数（MI）是大于1的，这表明2000—2012年中国工业低碳TFP总体上处于增长态势;但2012—2014年，低碳TFP指数（MI）均小于1，2014年后开始回升。纵观整个考察期间，不难发现，2000—2015年中国工业低碳全要素生产率经历了一段升降交替的“波浪式”变动过程。

从低碳全要素生产率指数（MI）的分解项来看，2000—2015年中国工业技术进步指数（TC）的均值为1.035，技术进步的年均增长率为3.5%;技术效率变动指数（TEC）的均值为1.007，年均增长率为0.7%;规模效率变动指数（SEC）的均值为1.001，年均增长率为0.1%。因此，考察期内技术进步、技术效率和规模效率对中国工业低碳全要素生产率的增长均具有正向影响，并且技术进步的推动作用明显大于后两者。从技术进步的两大分解因子—纯技术进步和动态进步来看，纯技术进步指数（TPC）的均值为1.149，动态进步指数（DPC）的均值为0.901，这表明技术进步的增长主要得益于纯技术进步水平的提高，动态进步对其具有阻碍作用;从技术效率的分解情况来看，环境效率变动指数（EC）和纯技术效率变动指数（PTEC）的年均值都大于1，说明这两者的正向作用共同推动了工业行业技术效率水平的提高。并且，两个分解项的年均增长率都不足1%，这反映出在考察期间中国工业的环境效率与纯技术效率的增长均较为缓慢[26]。

从表2可以看出，除了纺织业（A9）、皮革毛皮羽绒及其制品业（A11）这两个行业之外，其他行业的低碳全要素生产率指数的年均值均大于1，这表明在考察期间中国绝大多数工业行业的低碳全要素生产率实现了不同程度的提升。低碳全要素生产率的增速排在前五的工业行业依次为燃气的生产和供应业（A33）、专用设备制造业（A27）、有色金属矿采选业（A4）、印刷业记录媒介的复制（A15）和通用设备制造业（A26），以技术密集型行业为主。低碳全要素生产率增速最慢的五个行业依次为纺织业（A9）、皮革毛皮羽绒及其制品业（A11）、非金属矿物制品业（A22）、煤炭采选业（A1）和非金属矿采选业（A5）。并且橡胶和塑料制品业（A21）、石油加工及炼焦业（A17）及造纸及纸制品业（A14）这类污染密集型工业的低碳TFP增长率也同样非常缓慢，高耗能、高污染、低技术的行业特征导致了其低碳全要素生产率的低下。此外，从低碳全要素生产率的各分解项来看，全部工业行业的纯技术进步指数（TPC）的均值都大于1，这说明我国工业行业低碳全要素生产率的增长主要来源于技术进步[27-29]。

五、結论及政策建议

（一）结论

本文利用动态EBM-MI指数模型对2000—2015年中国工业33个行业的低碳全要素生产率及其分解项进行了测算，得出结论如下：

1.从纵向时间序列来看，在考察期间中国工业低碳全要素生产率指数大都围绕1波动，年均增长率为4.3%。具体来讲，2000—2003年持续增长，随后迅速降低，且在2004年降至最低后出现反弹，并于2005年达到峰值1.306;2005—2012年指数大致呈现“锯齿形”走势;2012年后再次上升。技术进步指数、技术效率变动指数及规模效率指数的年均值都大于1，且三者当中促进低碳全要素生产率的增长贡献最大的是技术进步。技术进步的增长主要得益于纯技术进步水平的提高，动态进步对其具有阻碍作用。纯技术效率变动指数及环境效率变动指数两者共同的正向作用推动了技术效率水平的增长[27，30-33]。

2.从分行业来看，2000—2015年绝大多数工业行业的低碳全要素生产率是增长的，且低碳TFP的增速具有较为明显的行业异质性：技术密集型、清洁型工业的增速明显高于其他行业，污染密集型工业的增速最为缓慢[34-36]。

（二）政策建议

1.努力深化与加快中国工业的低碳转型发展，以求早日在工业领域全面实现生产方式的“低碳化”。在实际的生产过程中应该处理好“投入—产出”二者的关系，即需从经济学的角度出发，以最少的要素投入追求最大的经济社会综合效益。同时，高度重视技术创新与技术进步，健全技术创新体系，提高企业内部的管理水平，积极引进低碳技术以及推行节能减排，这些措施对于低碳全要素生产率的提高都是非常有必要的。

2.继续推进产业结构的优化升级，使之成为我国工业低碳发展的不竭动力。坚持可持续发展的原则，注意协调好各类碳排放工业行业的发展规模和速度，优先发展高新技术、清洁型工业，限制污染密集型工业过快发展。政府可在政策和监管方面给予低碳清洁企业更多的支持，从而激励其开展低碳生产工艺的研发等技术创新活动，以助于提升我国工业整体的低碳全要素生产率。

[参考文献]

[1]Abramvitz M. Resource and out-put trends in the U.S. since 1870 [J].America Economics Review，1956（46）：5-23.

[2]Solow R M. Technical change and the aggregate production function [J]. Review of Economics and Statisticsm，1957（39）：312-320.

[3]Farrel M J.The measurement of productive efficiency[J]. Journal of the Royal Statistical Society，1957（12）： 253-281.

[4]Charnes A， Cooper W W， Rhodes E. Measuring the Efficiency of decision making units [J].European Journal of Operational Research，1978（2）：429-444.

[5]Banker R D， Charnes A， Cooper W W. Some models for estimating technical and scale inefficiencies in data envelopment analysis [J].Management Science，1984（30）：1078-1092.

[6]F?re R， Grosskopf S， Lindgren B， et al. Productivity Developments in Swedish Hospitals： A Malmquist Output Index Approach[M]// Data Envelopment Analysis： Theory， Methodology，and Applications. Springer Netherlands， 1994：227-235.

[7]Malmquist S. Index numbers and indifference surfaces [J]. Trabajos de Estadistica，1953（4）：209-242.

[8]Caves D W， Christensen L R， Diewert W E. The economic theory of index numbers and the measurement of input， output and productivity [J]. Econometrica，1982（50）：1393-1414.

[9]Chambers R G， Fare R， Grosskopf S. Productivity growth in APEC countries [J].Pacific Economic Review，1996（1）：181-190.

[10]Chung Y H， Fare R， Grosskopf S. Productivity and undesirable outputs： a directional distance function approach[J]. Journal of Environmental Management，1997（51）：229-240.

[11] 涂正革.环境、资源与工业增长的协调性[J].经济研究，2008（2）：93-105.

[12] 吴军.环境约束下中国地区工业全要素生产率增长及收敛分析[J].数量经济技术经济研究，2009（11）：17-27.

[13] 汪克亮，杨宝臣，杨力.考虑环境效应的中国省际全要素能源效率研究[J].管理科学，2010（12）：100-110.

[14] 屈小娥，席瑶.资源环境双重规制下中国地区全要素生产率研究—基于1996—2009年的实证分析[J].商业经济与管理，2012（5）：89-97.

[15] 岳书敬，刘富华.环境约束下的经济增长效率及其影响因素[J].数量经济技术经济研究，2009（5）：94-106.

[16] 陈诗一.中国的绿色工业革命：基于环境全要素生产率视角的解释（1980—2008）[J].经济研究，2010（11）：21-34.

[17]李涛，陈碧琴，何雪峰.技术存量效应、真实效率追赶与中国低碳TFP核算—基于RAM与序列Malmquist-Luenberger指數[J].管理工程，2013（3）：116-123.

[18]周五七，聂鸣.低碳转型视角的中国工业全要素生产率增长—基于1998—2010年行业数据的实证分析[J].财经科学，2012（10）：73-83.

[19]邓晓兰，鄢哲明.资源错配对中国工业低碳生产率影响的实证分析[J].财经科学，2014（5）：74-83.

[20]Porta R L， Lopez-De-Silanes F， Shleifer A. The economic consequences of legal lrigins[J]. Journal of Economic Literature，2008（46）：285-332.

[21]Egger H， Egger P.Labor market effects of outsourcing under industrial interdependence[J].International Economics&Finance，2005（14）：349-363.

[22]雷明，赵欣娜，张明玺.基于环境负产出的能效动态Malmquist 模型研究[J].数量经济技术经济研究，2012（4）：33-48.