用理学单“理”出数学学习的深度
2018-03-01刘大伟
刘大伟

【关键词】理学单;数学语言表达;数学思维;数学思想方法
【中图分类号】G623.5 【文献标志码】A 【文章编号】1005-6009(2018)81-0076-02
所谓“理学”,是整理性学习的简略说法。整理性学习重视学习的条理性、系统性和结构性,是一种有效的学习方式。理学单则是指学生运用文字、图示或者符号等自己喜欢的方式表达自己的学习过程,展示自己对某一数学问题的思考,是学生内化知识过程的体现。运用理学单学习数学,有助于提升学生数学语言表达的严谨性和科学性,帮助学生在知识之间建立联系,促进思维建构,提炼数学思想和方法,促进学生深度学习。下文以苏教版四下《三角形的分类》一课为例,探讨理学单对数学学习的价值。
1.“理”出语言表达。
新课标明确指出:“能清晰、有条理地表达自己的思考过程,做到言之有理,落笔有据;在与他人交流的过程中,能运用数学语言合乎逻辑地进行讨论与质疑。”数学是思维的体操,语言是思维的外壳。课堂上学生的发言是其思维的一次发展,是提升自我数学语言素养的一次机会。但课堂时间有限,无法让学生一一展示,或交流时间短暂,语言表达不够完整精练。理学单巧妙地解决了这一问题,帮助学生整合本节课的内容,在头脑中形成较为完善的结论,有条有理地写出自己的思考和想法。这既锻炼了学生的数学语言表达能力,也让学生的思维能力得到较好的发展。
尤其是文字形式的理学单(如图1),更能磨砺学生的语言表达能力。通过自我反思和梳理,也为学生后续知识的学习打下坚实的基础。
2.“理”出知识结构。
理学单有助于学生转变学习方式,将以往的被动学习变为自主自觉地学习。灌输式的教学方式教给学生的大多是零碎孤立的信息和知识,这些知识往往是不稳定的、不牢固的。而理学单能够帮助学生自主内化知识,引导学生透过现象看本质,找到知识的精华所在,理清知识的内在聯系,形成系统的知识网络,让学习真实发生。
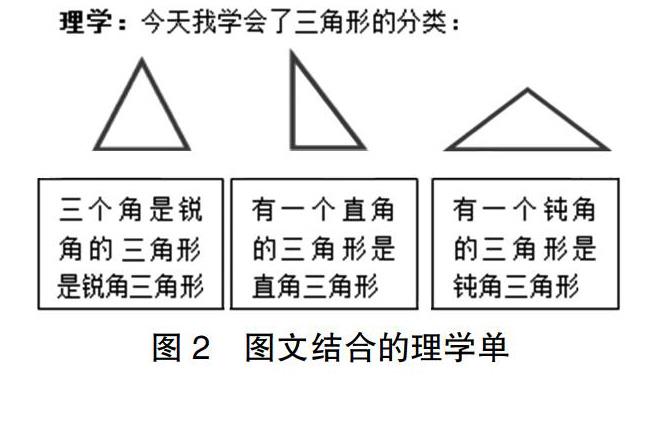
例如:在学习三角形的分类后,学生通过文字归纳出三种三角形的特征,配上对应的三种三角形图形,能更加清晰地表示三角形分类的知识结构(如图2)。
3.“理”出思维发展。
教育家赞可夫指出,在各科教学中要始终注意发展学生的逻辑思维,培养学生思维的灵活性和创造性。在数学教学中,教师要特别重视发展学生的思维,让每一个学生养成想问题、问问题、解决问题的习惯,而理学单正是提升学生思维的工具。一步一步地思考,一点一滴地整理,学生的思维在这个过程中得以发展和完善。
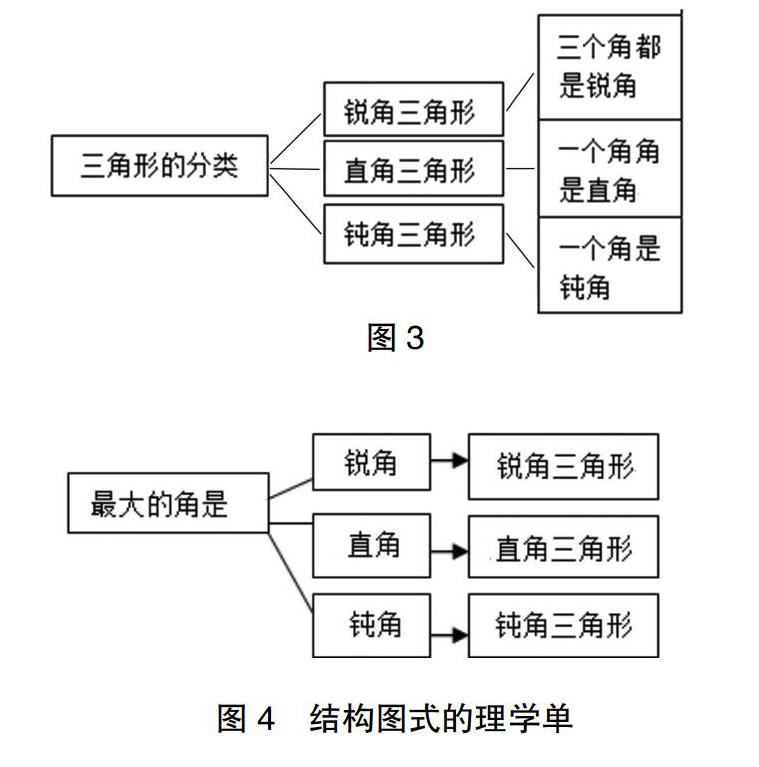
例如:结构图式的理学单(如图3和4)能清楚地表示出三类三角形及其角的关系。这两张结构图看似相同,其实不同:图3是按照角的特点进行三角形的分类,图4中的理学能抓住每类三角形的关键特征进行分类,进一步提炼出用三角形中“最大角”的标准来进行分类,其思维含量更高。
4.“理”出数学思想方法。
数学思想本质上是对数学知识的深刻认识,是对教学内容以及教学方式的抽象概括与规律性总结,同时也适用于解决数学问题的根本看法,贯穿于提出数学问题、分析数学问题、解决数学问题的整个过程,具有高度的概括性和抽象性。数学思想是数学的灵魂,数学方法是数学的行为,理学单正是学生展示数学思想方法的有效载体。学生在完成理学单的过程中,逐步将归纳思想、分类思想、符号化思想、对应思想等数学思想方法渗透其中。
例如:图5中的集合式理学单便诠释了三角形和锐角三角形、直角三角形、钝角三角形之间的关系,以文字备注出相应三角形的特征,使学生对图的理解和表达更加准确。这种形式新颖的理学单有助于学生自主学习、自我梳理的能力。学生通过多种形式的表达,理出了本课的知识脉络和线索结构。
一般来说“理学单”是在以单元为板块学习时设计使用的,而这节课是在学生掌握了角的分类后,对《三角形的分类》这一节课进行的理学尝试。本节课的理学不仅有线条式的“理”,还有结构化的“理”,通过图示、文字,思维导图等形式理出知识,不仅体现了定义概念和图示结构的整理,而且勾连了分类与归纳的方法,体现出学生在现场学习中的智慧和能力。
理学单的使用,促使教师在备课中关注学生的思维发展,不断思考如何能最大程度地让学生自主学,自主理,有利于帮助学生个体独立思考、碰撞思维,让思维向更深处发展,让学习真实有效地发生。
(作者单位:南京市建邺实验小学)
