城市轨道交通列车时刻表与车底运用整合优化模型

姚 宇，朱晓宁*，康柳江，廖正文,1b

(1.北京交通大学a.交通运输学院，b.轨道交通控制与安全国家重点实验室，北京100044；2.新加坡国立大学土木与环境工程系，新加坡117576，新加坡)

0 引言

随着城市交通需求的不断扩大，城市轨道交通凭借其快速、准点、运量大、安全性高等优势在城市公交系统中发挥着骨干作用[1].近年来，以提高服务水平、降低运输成本为目标的运行计划编制成为城市轨道交通运营管理的重要研究内容之一[2].

在理论研究方面，现有的研究通常将城市轨道交通的运行计划编制问题依次划分为4个部分：列车开行计划、列车时刻表、车底运用计划和乘务计划，并将前一部分的解决方案作为后一部分的前提和基础，通过迭代优化取得一个较优解.其中，时刻表规定各次列车在区间的运行时间、在车站的到发或通过时刻；车底运用计划则指派各车底承担相应的车次任务.国内外众多学者对以上2个问题进行过深入研究，或利用数学、运筹学等建模方法[3]，或利用现代启发式优化算法[4]进行求解.然而，上述大部分研究都是单独考虑2个子问题，或仅将车底数量作为保证时刻表方案可行的约束条件[5]，而未从系统的角度整体优化该问题.虽然分步求解子问题可以降低问题的复杂度，但是忽略了列车时刻表与车底运用之间的有机联系，导致求解结果具有局限性.回顾文献，仅有少部分研究针对这一整合问题，例如，王世峰建立了城轨列车时刻表与车底运用一体化双层规划模型[6]，但在求解方法上仍是采用了分步算法.Luis Cadarso等以马德里快速轨道交通为背景，构建了时刻表和车底改编作业的一体化模型[7]，但忽略了乘客候车时间.

基于上述既有研究成果中的不足，本文结合城市轨道交通运输组织的特点，充分考虑列车发车时刻与车底接续的相互联系，建立了时刻表与车底运用整合优化模型.

1 问题描述

1.1 线路组成

对于单条城市轨道线路，可将其上下行方向视为2条独立线路.如图1所示，每条线路有q座车站，S为车站集合，S={s|s=1,2,3,…,2q} ；L为运行方向集合，L={l|l=1,2}，l=1为上行方向，即从1站至q站，l=2为下行方向，即从q+1站至2q站；D为停车场集合，D={d|d=1,2}；R d为停车场d保有的车底集合，r∈R d⊂R.

图1 城市轨道交通线路示意图Fig.1 Illustration of urban railway transit line

1.2 车次任务与车底运用接续关系

构建城市轨道交通车次任务和车底运用接续关系图，如图2所示.节点表示列车出入车场或车次任务；实线弧表示车底r执行的车次任务间的接续，对应变量虚线弧表示车底r出入车场与车次任务之间的接续，分别对应变量

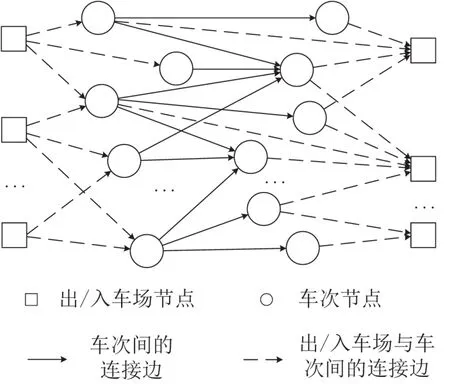
图2 车次任务与车底运用接续关系图Fig.2 Relationship diagram between train services and rolling stocks utilization

1.3 研究问题

车底是时刻表得以执行的保证，同时时刻表又是车底运用方案的基础，考虑到两者间的密切联系，本文将列车发车时刻和车底接续方案均作为决策变量，建立了列车时刻表与车底运用整合优化模型.模型已知条件、求解问题、核心决策变量及与图2中元素的对应关系如表1所示.

2 列车时刻表与车底运用整合优化模型

2.1 符号定义

为方便描述，本文对模型中涉及的主要参数和变量进行定义.

[0 ,T]——列车运营时段，τ∈[0,T]，每小时为1个时段；

J——车次任务集合分别表示l方向车次任务的集合和l方向在τ时段的车次任务集合；

U——拥挤度等级集合，U={u|u=1,2,3}；

表1 独立模型与整合模型对比Table 1 Comparison of independent models and integrated model

hmin,hmax——最小发车间隔和最大发车间隔；

ts——列车从s站行驶至s+1站的运行时间；

ttr——列车最短折返时间；

Al(t)——l方向时间t的乘客到达速率；

θu——拥挤度等级u对应的感知时间偏差系数；

Cu——拥挤等级u对应的列车能力；

Cf——车底固定保有费用；

Cr——车底执行1次车次任务的运行成本；

Vd——车场d的车底保有量；

Tj——车次j的发车时刻；

2.2 目标函数

(1)公司运营费用.

公司运营费用Zc包括2部分：车底固定保有费用和车底运行费用.前者为单位车底固定保有费Cf与上线运营车底总数的乘积，后者为单次车次任务的运行成本Cr与总车次数的乘积.

(2)乘客出行费用.

乘客出行费用包括购票费用、换乘时间费用、候车时间费用和乘车时间费用等，本模型考虑受时刻表影响的候车时间费用Zp，乘车时间费用Zt和滞留乘客的时间费用Zd.

假设在同一时段内到达的乘客服从均匀分布，则乘客的候车时间可以表示为候车人数乘以发车间隔的1/2.乘客总候车时间为

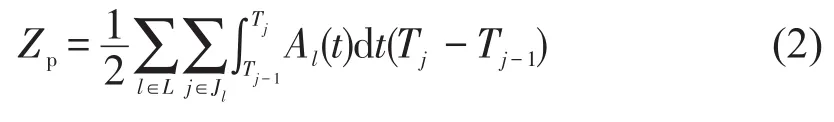
实际乘车时间是指乘客从进入车厢至到站后离开车厢所经历的时间，但车厢内的拥挤环境会造成乘客对乘车时间的感知偏差[8].本文将车厢内的乘客拥挤度分为3个等级，用u表示.当u=1时，乘客有较大站立的空间，可自由走动；u=2时，车厢处于中度拥挤状态；u=3时，车厢处于拥挤状态且无法容纳更多乘客.乘客在拥挤度等级为u时感知的乘车时间为实际时间的(1+θu)倍.因此，乘车时间Zt由乘客实际乘车时间和拥挤环境造成的偏差感知时间2部分组成.

拥挤环境不仅会造成对时间的感知偏差，当车厢内乘客数达到饱和时，未上车的乘客只能在站台等候下次列车，滞留乘客的惩罚系数用ξ表示，总时间费用Zd为

通过乘客平均时间价值μ将乘客费用的时间单位转换为经济单位，模型的总目标函数为公司运营和乘客出行的总费用Z最少.

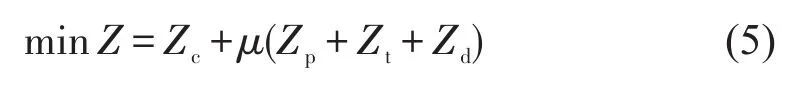
2.3 约束条件

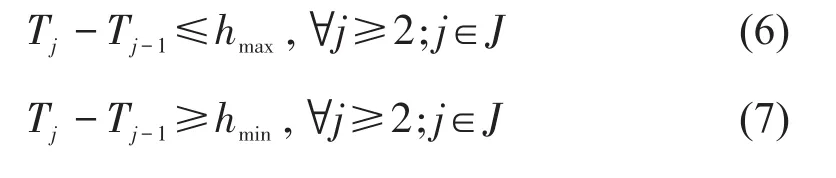
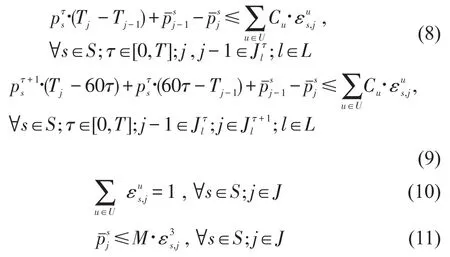
约束条件式(6)～式(11)是时刻表相关约束：式(6)和式(7)为发车间隔上下限约束；式(8)和式(9)分别为相邻列车处于同一时段和不同时段下的“车流耦合”约束，即列车车次和客流需求之间的匹配关系，表示断面客流需求减去滞留乘客数应小于等于列车在对应拥挤度等级下的运力；式(10)表示列车在每个区间的拥挤度等级唯一；式(11)表示只有在车厢内乘客达到饱和时才会产生滞留乘客，M为一个足够大的正数.

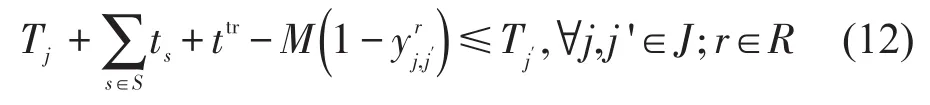
式(12)是联系时刻表与车底运用问题的关键约束，表示同一车底依次执行2次车次任务时，必须满足相应的时间约束.

约束条件式(13)～式(15)表示车底运用与车次任务之间的匹配关系：式(13)表示每一车次都有1个前驱点与之相连，前驱点可以是车次任务，也可指车底从车场发车；同理，式(14)保证每一车次节点都有1个后继节点相连；式(15)为同一车底约束，即每个车次节点的前驱和后继节点都由同一车底连接；式(16)表示所有的车底只能从车场发出1次；式(17)表示从d车场发出的车辆数应小于该车场的列车保有量.

2.4 模型的线性化处理

目标函数中的乘客总候车时间Zp为非线性表达式.候车时间取决于列车发车间隔，当发车数确定时，乘客总候车时间随发车间隔之间的偏差增大而增大.本文引入0-1变量，通过分段化处理使Zp线性化；定义为l方向τ时段的理想发车间隔，即该时段内总偏差为0的发车间隔；定义与理想发车间隔之间偏差等级的集合N={n|-5≤n≤5}，且n为整数，当列车j与前车的实际发车间隔和理想发车间隔之间的偏差等级为n时否则为0.对应增加约束条件式(18)～式(20).

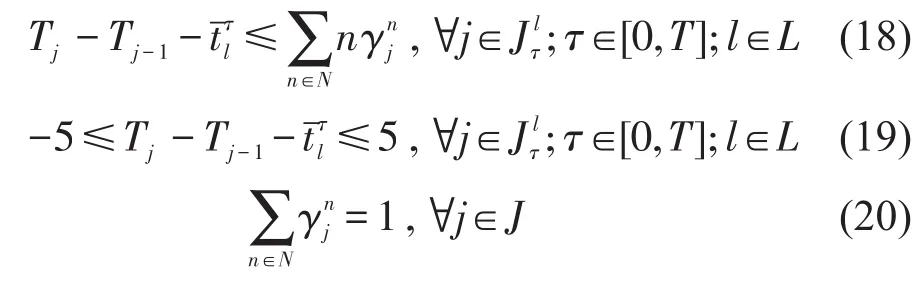
实际发车间隔与理想发车间隔的差值对乘客候车时间的影响可由式(21)算出，其中是l方向在τ时段平均每分钟的到达人数.则乘客总候车Zp的近似线性化表示为第1部分表示理想发车间隔下乘客的总候车时间，第2部分为变化部分.

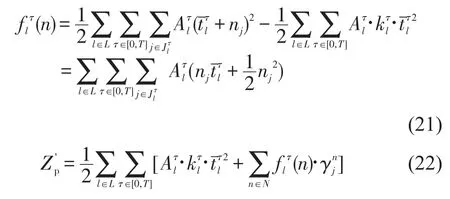
总目标函数变为

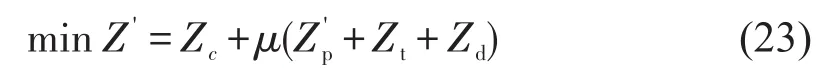
综上，本文最终构建的混合整数线性模型为目标函数，即式(23)；约束条件为式(6)～式(20).经测试，该模型可用CPLEX软件在一定时间内求得全局最优解.

3 实例分析

3.1 基本信息及参数取值

以2015年7月北京市地铁亦庄线的实际运营情况为基础进行案例分析，该线路运营长度23 km，共有13座车站.研究运营时段为6:00-8:00，研究时段站间断面客流量如表2所示.

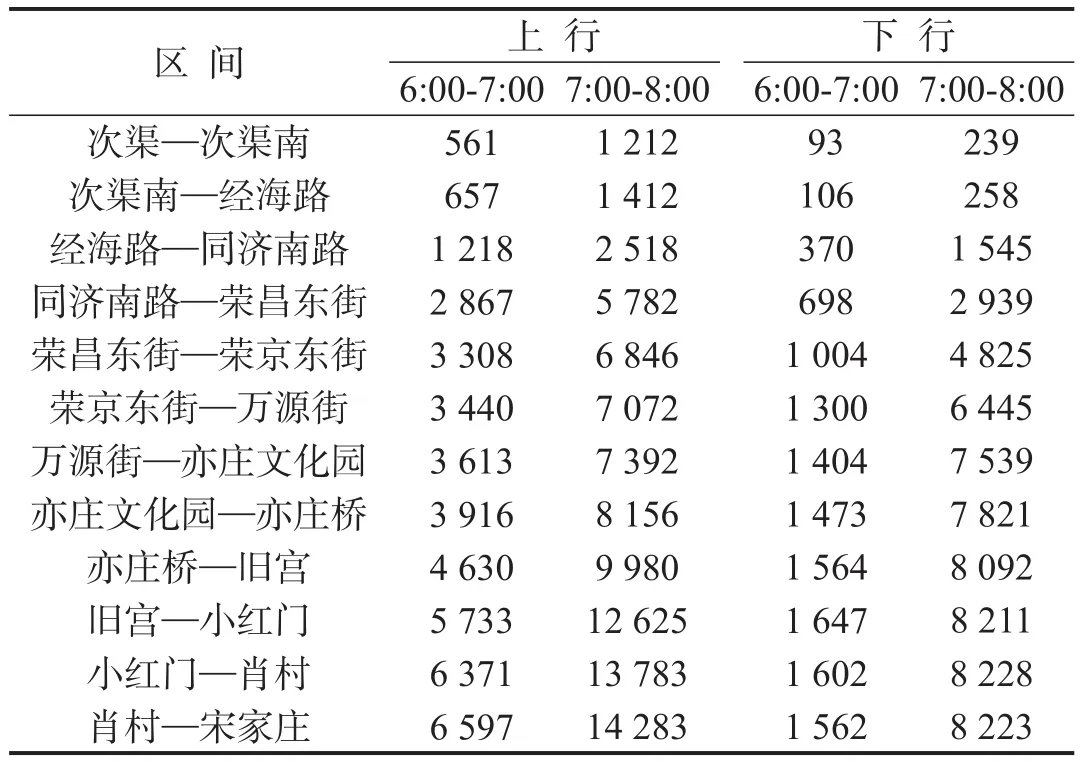
表2 研究时段断面客流Table 2 Transect volume during study hours

其他参数取值如下：当车厢内乘客密度小于6.0人/m2时，u=1，C1=1 468人/车；乘客密度为6.0～7.5人/m2时，u=2，C2=1 752人/车；乘客密度为7.5～9.0人/m2时，u=3，C3=2 037人/车.车底保有成本利用城市轨道交通车辆全寿命周期成本计算模型[9]进行计算，车底日均保有成本=(车辆购置费用+维修费用+处置成本-残值)/全寿命周期，可估算出Cf=5 000元/列，单次车次任务的运行成本为单位里程成本[10]与线路里程的乘积，计算得Cr=60×23=1 380 元.θ1=0，θ2=1.5，θ3=2，ξ=15，hmin=2min，hmax=12 min，列车最短折返时间ttr=4 min.2015年北京市职工年平均工资为85 083元，计算得乘客平均时间价值

3.2 结果分析

模型运行的硬件环境为Intel(R)Core(TM)i5-4210U CPU@2.40GHz，内存为4GB；软件环境为Windows10系统，使用PYTHON调用ILOG CPLEX12.7.1对模型进行求解.

根据实例中上下行客流需求相差较大的特点，本文考虑了城市轨道交通运输组织中通常使用的成对发车和非成对发车2种模式，利用上述时刻表与车底运用整合优化模型进行求解，并与分步优化模型的求解结果进行对比，分步优化模型的解是先求解列车时刻表子模型，再将其结果作为输入求解车底运用子模型计算得到，求解结果对比如表3所示.

表3 模型求解结果比较Table 3 Comparison of results by different models

其中，成对开行方案中，上下行方向列车开行对数一致，6:00-7:00和7:00-8:00分别开行列车6列和9列；非成对开行方案中，上行方向列车在2个时段分别开行6列和9列列车，下行方向均开行6列列车.

比较整合优化模型与分步优化模型，在2种运行模式下整合模型均有明显的优化效果，在乘客成本变化可接受的前提下，有效地缩减了所需车底数量，降低了企业运营成本.以成对开行方案为例，总费用下降了3.37%，其中，上线车底数量减少了2列，公司运营费用下降了8.71%；同时，乘客平均出行时间仅增加1.16 s，拥挤度等级未改变，总乘客出行费用仅增加0.10%.

比较成对开行与非成对开行2种运行模型，在分步模型的计算结果中，非成对开行方案的乘客出行费用和公司运用费用均高于成对开行方案，这是由于非成对开行的运输组织方案较为复杂，如果不对发车时刻和车底运用方案综合考虑，会造成车底的不充分利用和成本的增加.而在整合优化模型计算结果中，非成对开行方案的总费用小于成对开行方案.因此，对于方向不均衡明显的线路或时段，采用适应客流的非成对开行方案，利用整合优化模型求解，可以提高列车满载率，节约运营成本.

综上所述，结合客流需求特征选择相应的运行模式，利用本文提出的整合优化模型进行求解，可以达到乘客和公司利益的综合最优.列车发车时刻及车底运用方案最优解如表4所示.

绘制相应的列车运行图，如图3所示，斜线表示列车运行线.

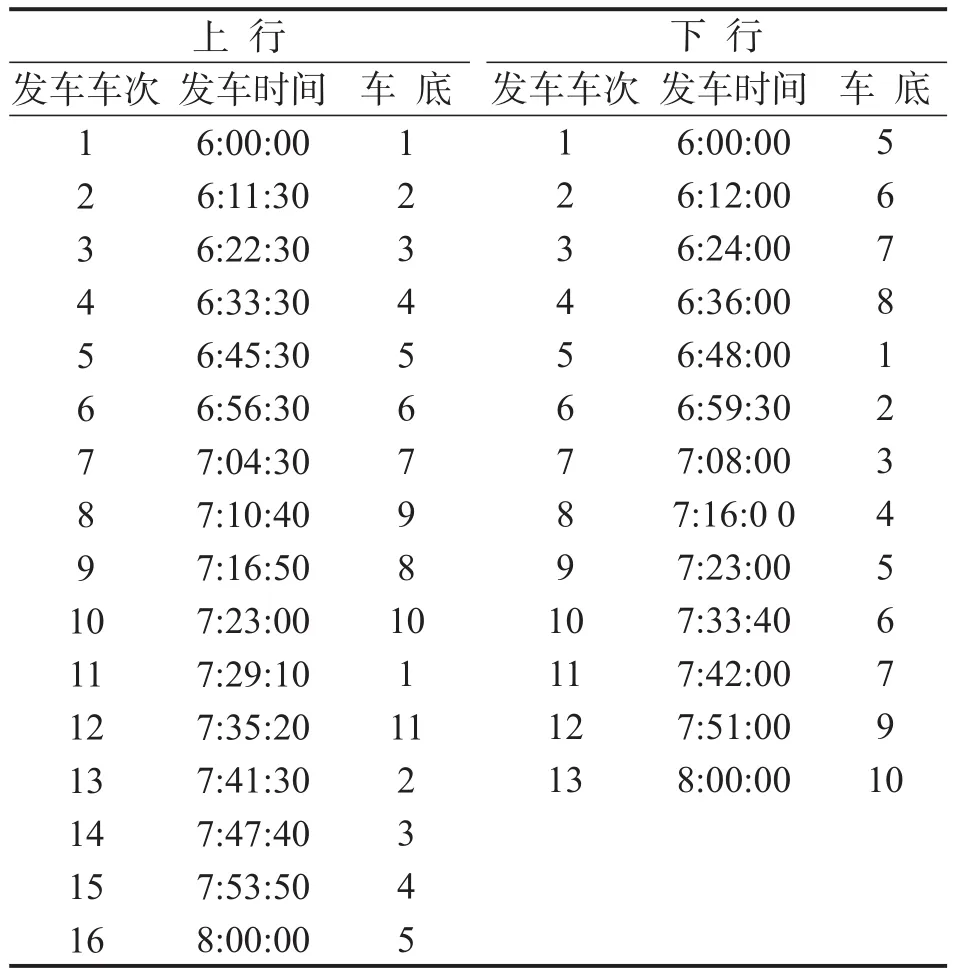
表4 列车发车时刻及车底运用计划Table 4 Train departure times and rolling stock schedules

图3 列车运行图Fig.3 Optimal train timetables

4 结论

本文综合考虑了列车时刻表和车底运用之间的有机联系，结合客流需求，构建了基于单条线路的城市轨道交通列车时刻表与车底运用整合优化模型，并提出了模型线性化处理方法，利用CPLEX在可接受时间内求得最优解，生成了列车时刻表和车底运用计划，优化效果明显.最后以北京地铁亦庄线为例进行了实例分析，并得出以下结论：

(1)对时刻表和车底运用方案进行综合考虑，可以在保证服务水平的前提下减少上线运营的车底数量；

(2)选择和客流特征相匹配的运行模式，可以有效地避免运能浪费，节约运营成本.

此外，在实际运营中，多线路的协调调度和统一指挥可以减少旅客换乘时间，同时促进车底和车场等资源的合理运用.因此，进一步考虑网络化运营下的列车时刻表和车底运用整合优化将是下一步研究的主攻方向；其次，停站方案、乘务组排班计划等问题也与时刻表及车底运用方案间存在必然联系，如何将这些问题与本文研究结合也将是今后研究的主要内容.

[1]KANG L,ZHU X,SUN H,et al.Modeling the first train timetabling problem with minimal missed trains and synchronization time differences in subway networks[J].Transportation Research Part B Methodological,2016(93):17-36.

[2]KANG L,WU J,SUN H,et al.A case study on the coordination of last trains for the Beijing subway network[J].Transportation Research Part B,2015,72(72):112-127.

[3]宁丽巧,赵鹏,徐文恺,等.城市轨道交通末班车时段时刻表协同优化研究[J].交通运输系统工程与信息,2016,16(6):108-114.[NING L Q,ZHAO P,XU W K,et al.Timetable synchronization optimization for urban rail transit in the last trains’hour[J].Journal of Transportation Systems Engineering and Information Technology,2016,16(6):108-114.]

[4]郑锂,宋瑞,肖赟,等.网络化运营下城市轨道交通列车车底运用计划编制的优化方法[J].中国铁道科学,2014,35(2):104-110.[ZHENG L,SONG R,XIAO Y,et al.Optimization method for working out vehicle scheduling plan of urban rail transit under network operation[J].China Railway Science,2014,35(2):104-110.]

[5]牛惠民,陈明明,张明辉.城市轨道交通列车开行方案的优化理论及方法[J].中国铁道科学,2011,32(4):128-133.[NIU H M,CHEN M M,ZHANG M H.Optimization theory and method of train operation scheme for urban rail transit[J].China Railway Science,2011,32(4):128-133.]

[6]王世峰.基于动态客流的城市轨道交通列车时刻表与车底运用一体化优化模型和算法研究[D].北京:北京交通大学,2016.[WANG S F.Study on integrated train timetabling and rolling stock scheduling model and algorithm based on time-dependent demand for urban rail transit[D].Beijing:Beijing Jiaotong University,2016.]

[7]CADARSO L,ÁNGEL MARÍN.Integration of timetable planning and rolling stock in rapid transit networks[J].Annals of Operations Research,2012,199(1):113-135.

[8]NIU H,ZHOU X.Optimizingurban rail timetable under time-dependent demand and oversaturated conditions[J].Transportation Research Part C,2013,36(11):212-230.

[9]JUN H K,KIM J H.Life cycle cost modeling for railway vehicle[C].International Conference on Electrical Machines and Systems,IEEE,2007:1989-1994.

[10]中国交通运输协会.城市轨道交通运营绩效评估体系成果报告2015[R].北京:中国交通运输协会,2015.[China Communications and Transportation Association.Report of metro operation performance evaluation system for 2015[R].Beijing:China Communications and Transportation Association,2015.]