基于随机机会约束规划的班轮联盟舱位租赁最优分配

陈继红，杨 晨，真 虹 ，张方伟，于 航，郑师禹

(1.上海海事大学交通运输学院，上海201306；2.上海国际航运研究中心，上海200082;3.美国罗格斯大学土木与环境工程学院，皮斯卡塔韦NJ 08854-8018，美国)

0 引言

面对持续低迷的航运市场和激烈的市场竞争，各大集装箱班轮公司纷纷通过组建班轮联盟来降低其系统成本，增加市场竞争力.随着班轮联盟的迅速发展，班轮联盟及其优化等问题的研究越来越全面[1-2].如今，针对联盟中已经投入合作的船舶、航线等进行合理的调度，联盟各成员之间合理的舱位分配等问题成为研究的重点.在过去的研究中，学者从不同研究角度和方法入手，探讨了大量有关班轮航线和舱位分配优化的问题.卜祥智等[3]基于收益管理的理念，建立了一个海运集装箱舱位分配与路径选择优化模型.陈继红等[4]在传统的班轮配船模型中考虑联盟箱位租用的影响，构建了1个新的班轮配船模型.Agarwa等[5]考虑了航运业收益管理发展趋势的不同特点，建立了集装箱多航段多产品和空箱调运能力分配的鲁棒优化模型.Fransoo等[6]从联盟的角度出发，基于成本最低建立了1个联盟下的空箱调运优化模型，用以研究联盟下的空箱调运问题.Parola等[7]利用网络流量的观念研究海运集装箱排程问题.Chen[8]等研究了联盟舱位互租模式下的舱位分配问题.此外，随机机会约束规划方法也被应用到舱位分配和运输路径优化的研究中.杨楠[9]建立了空箱调运的随机机会约束规划模型.朱萧篥等[10]构建了随机条件下运输问题的机会约束规划模型，并设计合适的混合智能算法进行求解.

纵观国内外的文献，许多都是基于确定条件下对联盟中单个班轮公司的舱位最优分配进行研究，而从联盟系统层面研究舱位协同分配的文献较少.随着联盟数量和规模的扩大，班轮联盟系统下舱位租赁分配优化显得更为复杂，尤其是在不确定需求的环境中.本文结合实际，分析并研究不确定需求下班轮联盟舱位租赁及分配优化的相关问题，构建了1个舱位租赁最优分配模型，并应用到舱位分配决策及实证分析中.

1 集装箱班轮联盟舱位租赁模式

班轮联盟始于1996年初，近几年发展极为迅速，尤其是联盟之间运力资源的合作.其中舱位租赁(Space/Slot Charter)[11]是合作中最为基础的模式，如图1所示.它是指自身在不投入船舶的情况下，通过向某航线上拥有舱位的其他经营人租用一定量舱位的方式来经营相关航线，并定期支付舱位租赁费.

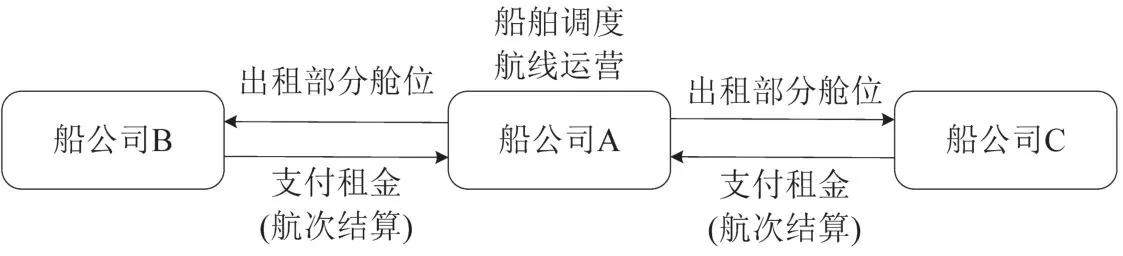
图1 舱位租赁模式示意图Fig.1 Space charter mode diagram

舱位租赁的特征主要体现在经营独立性、舱位配置不确定性及复杂性.通常情况下，联盟各成员主要进行舱位租赁数量权衡和舱位租金结算，其他运营业务和资金保持独立.舱位配置不确定性主要是指班轮联盟中各成员在某一具体航次上集装箱舱位需求的不确定性，其又体现在联盟内舱位需求的数量、运输时间、挂靠港口起讫对等多个方面.班轮联盟涉及多个成员，港口起讫对的不同及集装箱箱型的不同等多方面的因素会造成舱位配置非常复杂，多家船公司舱位配置的难度要远远大于一家公司.

2 不确定需求下的舱位租赁最优分配模型

2.1 不确定需求下的舱位最优分配模型的建立

实际情况中，集装箱的运输需求受季节性多种情况的综合影响，导致每个港口起讫对之间的集装箱运输需求具有不确定性，往往近似服从正态分布规律.除此之外，考虑到实际海运业务中的船舶舱容、吨位、重箱空箱需求等限制，以及签署的联盟协议中不同箱型舱位及插座的租赁数量限制，本文以合作航线上班轮联盟的最大收益为决策目标，构建模型为

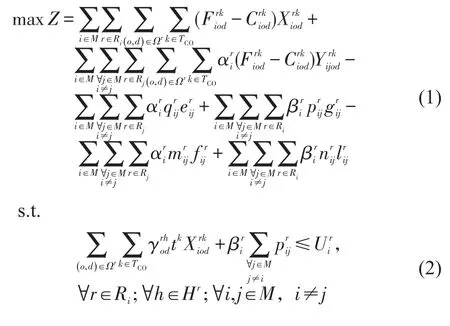
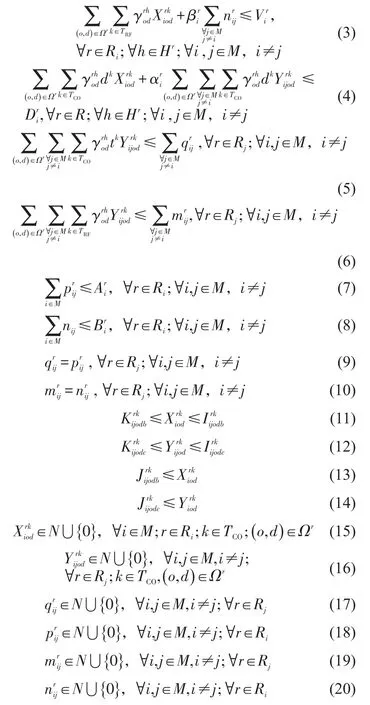
式中：Z——联盟总收益；

i,j——联盟各方；

o,d——港口；

k——箱型，包括20/40英尺重、空干货箱、冷藏箱和开顶箱；

r——航线类别，自营航线或合作航线；

h——航段类别；

M——联盟方集合，M={1 ,2,…,i,j,…} ,∀i,j∈M,i≠j；

Ri——表示联盟方i纳入联营范围的自有航线；

Rj——表示联盟方j纳入联营范围的合作航线；

TCO——所有集装箱集合；

THV——重箱集合；

TET——空箱集合；

TGP——干货箱集合；

TRF——冷藏箱集合；

TOT——开顶箱集合；

Ω——所有经停港口起讫对(o,d)的集合；

Ω r——合作航线r上所有港口起讫对集合；

H——所有合作航线中各航段所组成的集合；

H r——表示合作航线r中各航段所组成的集合；

d k——各种箱型对应的载重量系数；

目标函数如式(1)所示.在约束条件中，式(2)为船舶舱容限制，它表示分配的舱位之和不能超过联营船舶的最大舱容；式(3)为船舶冷藏容量限制，它表示舱位出租方所提供出租的冷藏插座数与其自用的冷藏插座数之和不能大于Vi；式(4)为船舶载重吨限制，它表示所有分配舱位的货物重量必须满足船舶总载重吨的限制；式(5)～式(10)为舱位及冷藏插座租赁限额，它表示舱位租赁数量之和与冷藏插座租赁数量之和必须满足租赁限额；式(11)～式(14)分别为重箱、空箱舱位需求限制，且均为随机需求；式(15)～式(20)为非负整数约束.

2.2 不确定优化模型的随机机会约束规划方法

由于重箱、空箱舱位需求为随机需求，本文考虑将机会约束规划问题转化为等价的确定性数学规划问题来求解.

设随机向量ε退化为1个随机变量ε，其分布函数为φ.若函数形如这样的形式，那么，当且仅当其中

当约束条件以置信度αj成立，即

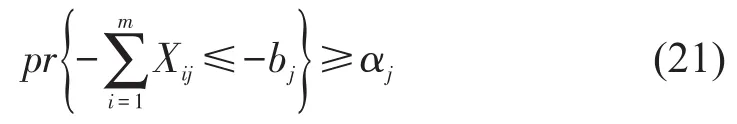
则运用上述定理可转化为

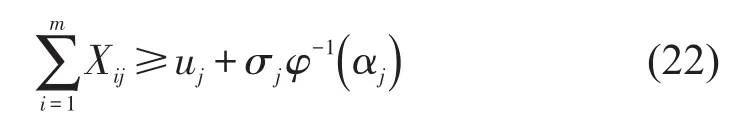
运用以上随机机会约束规划的思想，可将上述不确定需求下的舱位最优分配模型转化为1个单目标的线性规划模型，便于利用成熟的软件进行求解，本文将使用Lingo软件对实例进行求解.

3 算例应用研究

3.1 算例描述与模型规模

在亚洲—欧洲的一个完整航次上，A公司在自有航线上出租舱位给B公司和C公司.三方签订联盟租赁协议，其航线如图2所示，所经过的港口依次是上海(SHA)—宁波(NGB)—香港(HKG)—南沙(NSH)—汉堡(HAM)—鹿特丹(RTM)—费利克斯托(FXT)—新加坡(SIN)—南沙(NSH)—上海(SHA).

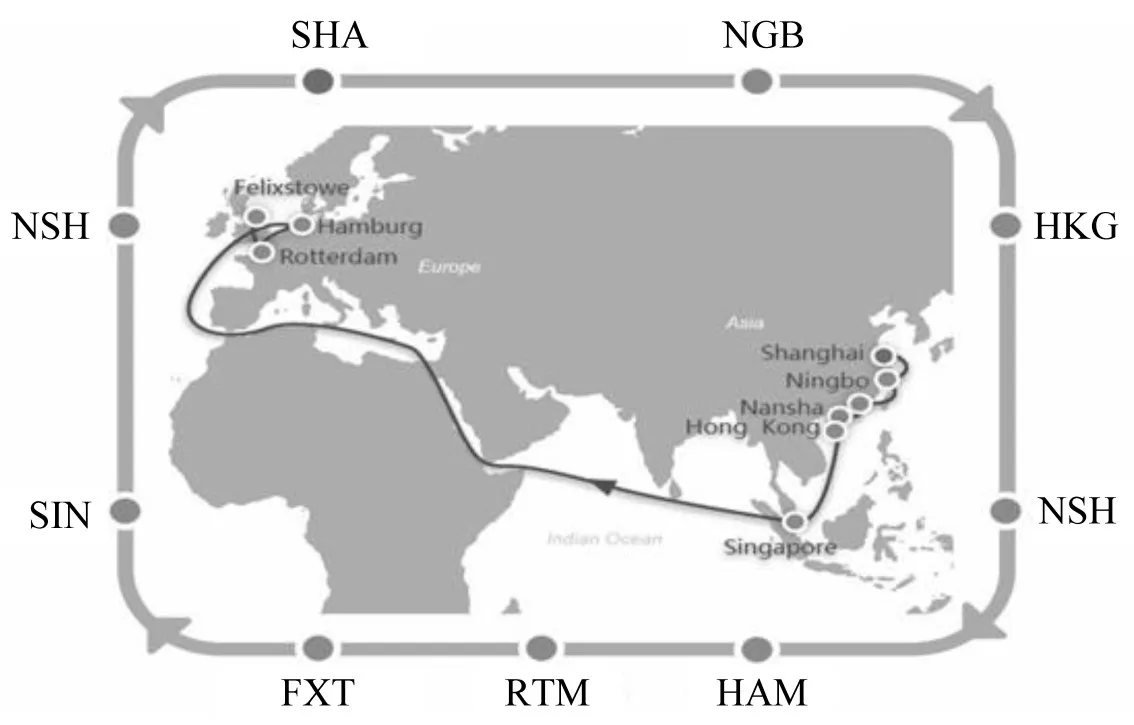
图2 实例航线图Fig.2 Shipping line of the case

在该航线上，A公司投入9 500 TEU、总载重吨135 000 T的海船，冷藏插座数为1 400个.本文重点研究12种箱型，包括20/40GP重空箱、20/40RF重空箱和20/40OT重空箱，其中20英尺箱和40英尺箱分别占1个和2个舱位.舱位和冷藏插座租赁限额分别为5 000 TEU和800个.

本文运用LINGO 11软件对不确定需求下班轮联盟舱位租赁的舱位配置单目标线性规划模型进行求解.求解硬件和系统分别为：英特尔I5处理器，内存8.00GB；操作系统为Windows 8.1(64位).该模型采用分支定界算法(B-and-B)，约束条件规模为2 178个，整数变量规模为1 765个，非零整数规模为35 872个.

3.2 优化结果分析

最终求解结果为A公司利润为4 049 531美元，B公司利润为1 087 883美元，C公司利润为881 092美元.B公司租进舱位量和冷藏插座量分别为2 806个和431个，C公司租进舱位量和冷藏插座量分别为2 194个和369个.

A、B、C公司在各个港口上各种箱型的配置量如表1～表3所示.

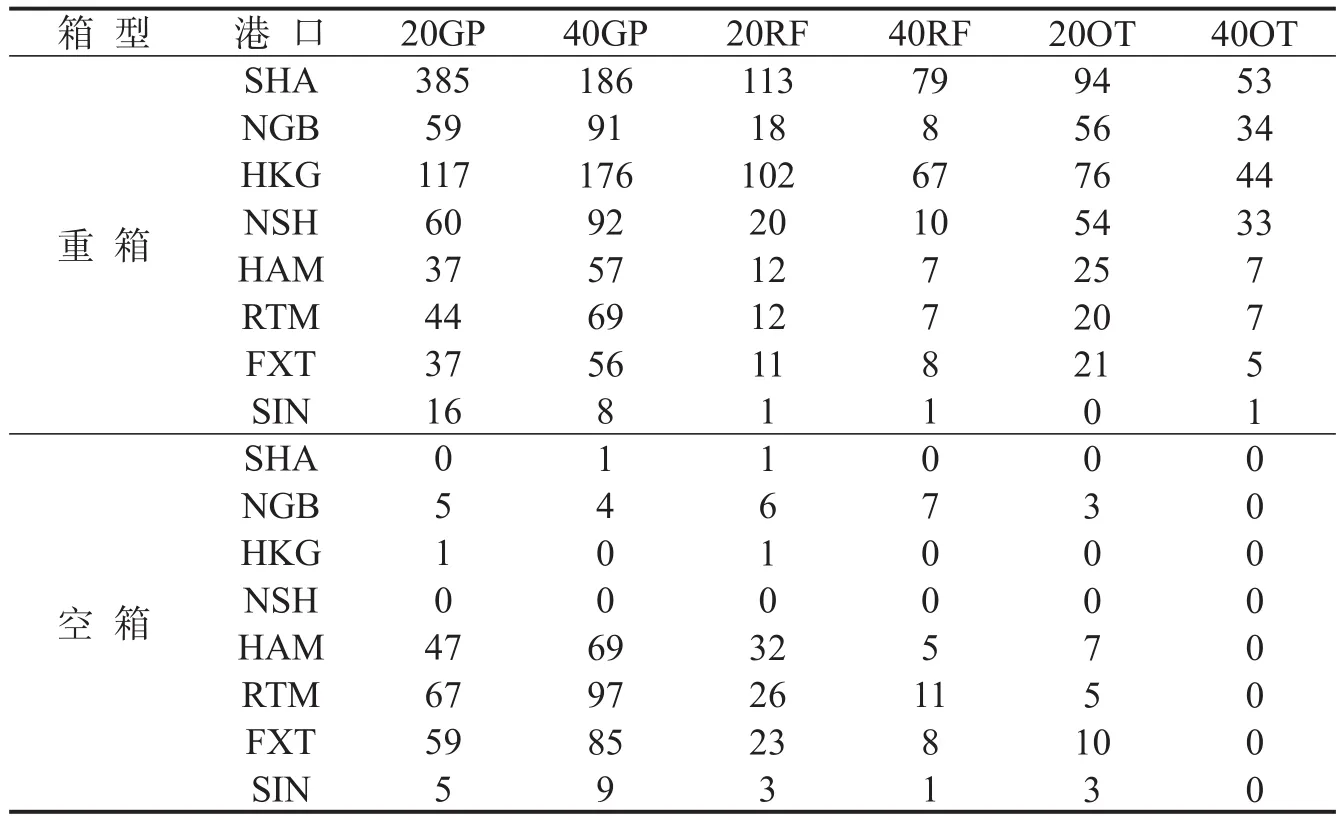
表1 A公司在各个港口上各种箱型分配量Table 1 Allocation of all kinds of container type in each port of A company

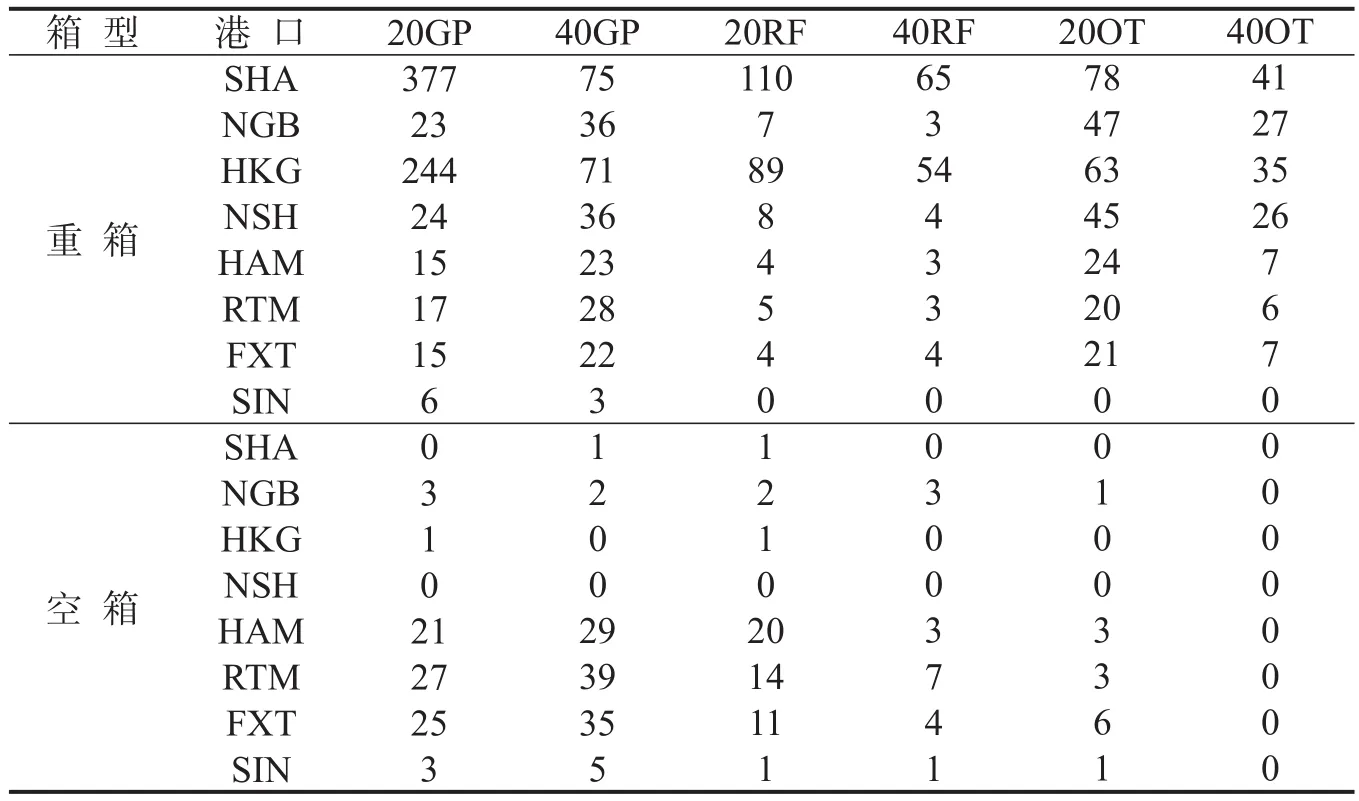
表2 B公司在各个港口上各种箱型分配量Table 2 Allocation of all kinds of container type in each port of B company

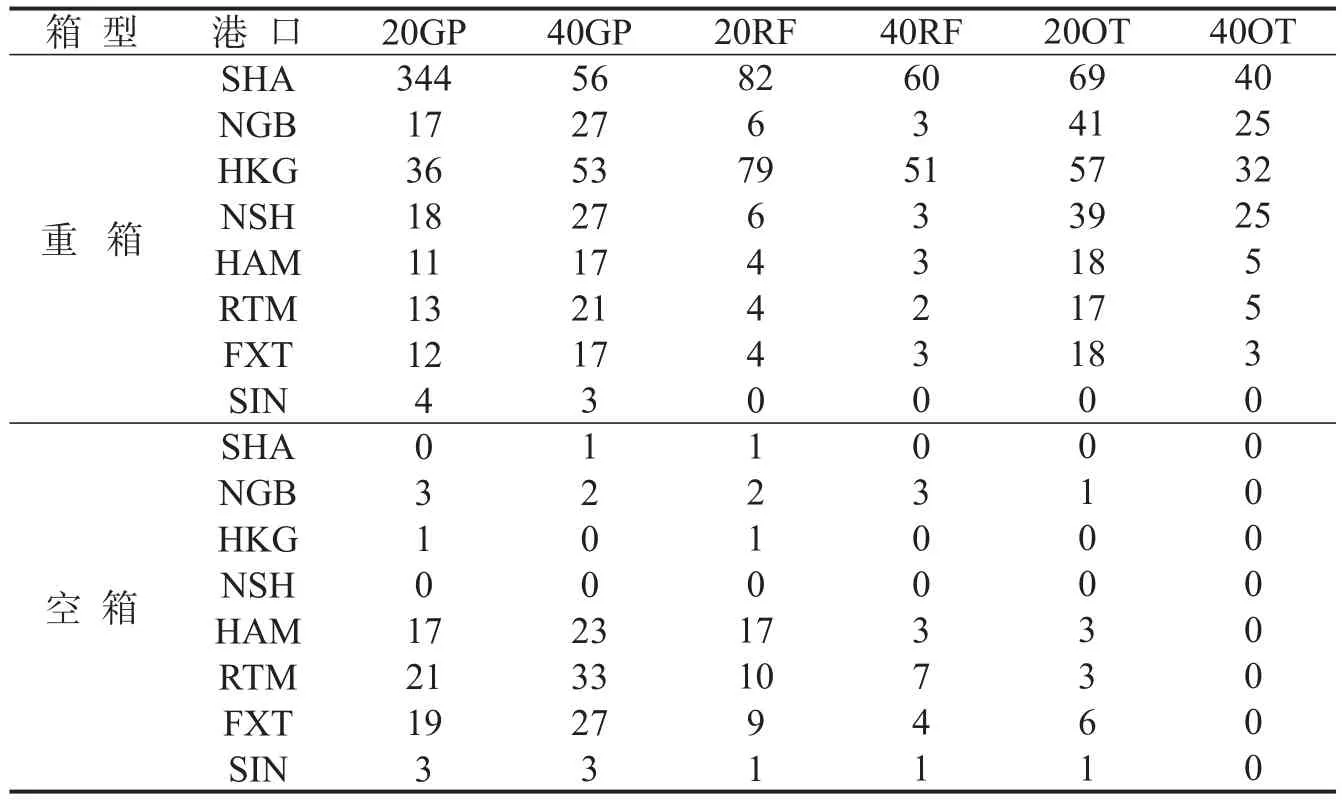
表3 C公司在各个港口上各种箱型分配量Table 3 Allocation of all kinds of container type in each port of C company

为了更加清楚直观地看出联盟各方在各港口舱位分配的规律，经统计得出联盟各方各港口舱位分配标箱量，如图3～图5所示.

具体分析结果如下：

(1)在该航线港口起讫对间，A、B、C公司重箱各箱型货种东西流向比(东西流向指的是案例中亚欧航线的正向航程及反向航程)分别为23.14%、14.92%和15.38%，这体现了东西航向的贸易不平衡，符合当前国际集装箱运输市场的实际情况.

(2)除了由于普通箱需求较大分配的舱位较多之外，重箱舱位优先分配给冷藏箱和开顶箱，这是因为这2种箱型的收益相对较高，因此优先满足冷藏箱和开顶箱的运输需求，满足收益最大化原则.

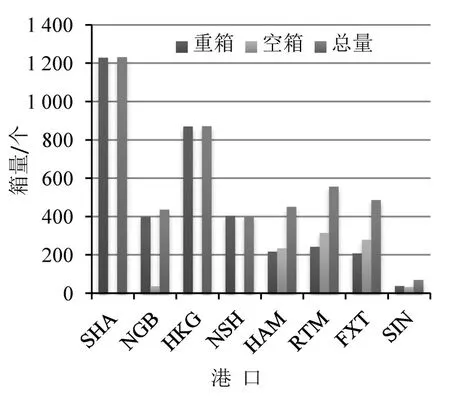
图3 A公司各港口舱位分配标箱量Fig.3 The amount of standard containers in each port of A company

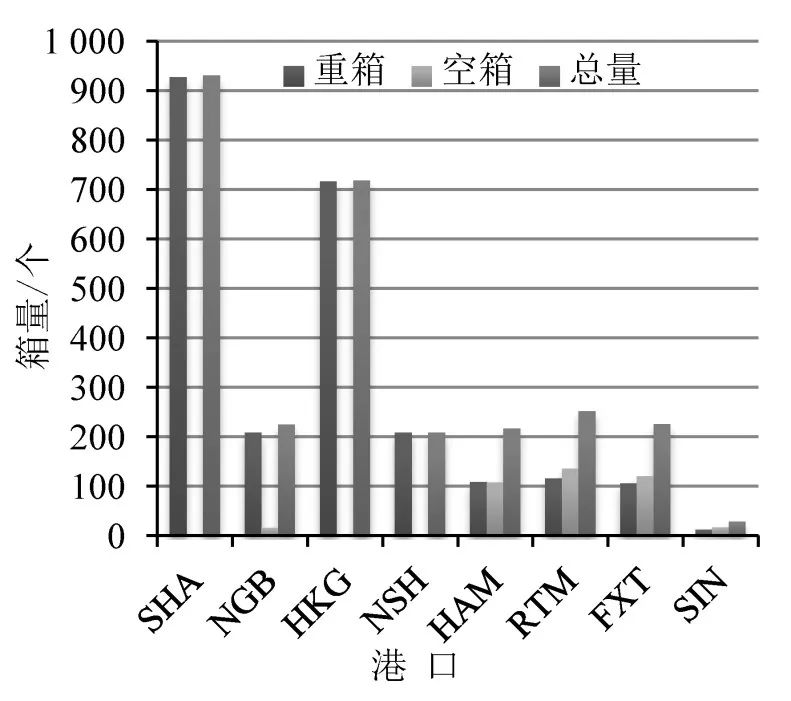
图4 B公司各港口舱位分配标箱量Fig.4 The amount of standard containers in each port of B company

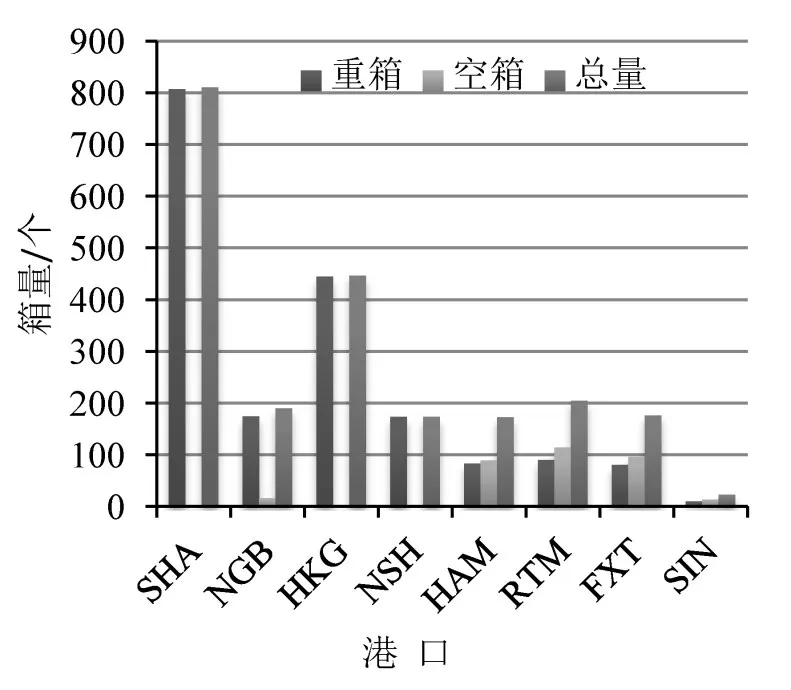
图5 C公司各港口舱位分配标箱量Fig.5 The amount of standard containers in each port of C company

(3)该航线为亚欧国际干线，重箱主要分配到亚洲区域，空箱主要分配到欧洲区域，同一区域内的重箱舱位分配量非常少，其运输任务主要由支线运输来承担.

(4)各港口各箱型的舱位分配结果体现了该航线上各港口在国际贸易中地位的不同.亚洲区域，上海港和香港港的舱位分配量高达40.91%和28.95%，欧洲区域，鹿特丹占比37.29%，由此可以判断上海港、香港港和鹿特丹港分别是亚洲和欧洲区域重要的枢纽港或中转港.

3.3 灵敏度分析

为了检验本文所构建的模型并研究重要参数的变化对模型中目标函数的影响，本文设计了5组实验，分别对运输货物的单位运价、舱位成本、航次可用运力、总冷藏插座数和舱位租赁费用进行灵敏度分析，其中每组实验进行时均保持其他参数不变，并按照-20%，-15%，-10%，-5%，5%，10%，15%，20%来调节参数大小，最后用图形来展示联盟总收益结果，如图6所示.

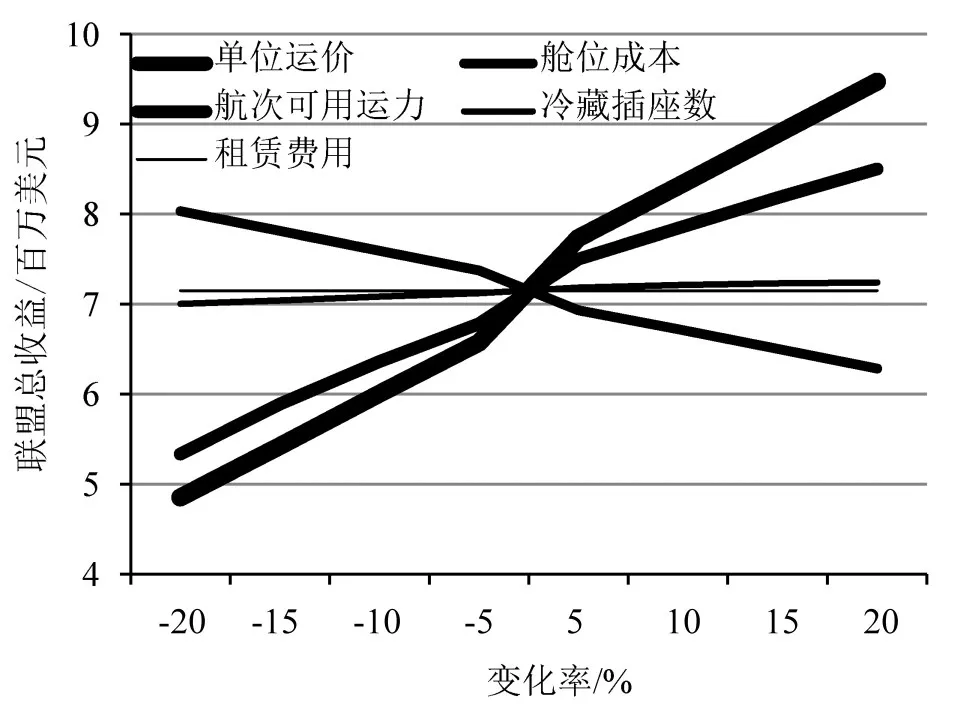
图6 5种参数与联盟总收益的关系Fig.6 The relationship between the five parameters and the total income of the alliance

通过5组实验的灵敏度分析，可以看出，单位运价、航次可用运力、总冷藏插座数与联盟总收益呈正相关，舱位成本与联盟总收益则呈负相关，舱位租赁费用不影响联盟总收益.其中，单位运价斜率的绝对值最大，即对联盟总收益的影响最大，因此，制定合理的运价是收益的最大保证.

4 结论

班轮联盟是目前集装箱班轮运输发展的主要趋势，本文在考虑航运市场不确定需求的基础上，研究了班轮联盟系统舱位租赁最优分配问题，构建了1个班轮联盟舱位租赁最优分配模型，并基于随机机会约束规划方法对模型进行了处理.根据调研数据与资料，对联盟系统舱位租赁模式下舱位的最优分配问题进行了详尽的实例研究，结果与事实相符，体现了班轮联盟系统舱位配置的协同性，同时也验证了方法和模型的有效性和实用性.

[1]PANAYIDES P M,WIEDMER R.Strategic alliances in container liner shipping[J].Research in Transportation Economics,2011,32(1):25-38.

[2]LEWANDOWSKIK.Alliance of marine container carriers-back to the cartels[J].Logistics and Transport,2015,26(2):21-32.

[3]卜祥智,赵泉午,陈荣秋.基于收益管理的海运集装箱舱位分配与路径选择优化模型[J].管理工程学报,2008,22(3):94-99.[BU X Z,ZHAO Q W,CHEN R Q.An optimization model of ocean shipping container slot allocation and routing choice problem based on revenue management[J].Journal of Industrial Engineering and Engineering Management,2008,22(3):94-99.]

[4]陈继红,真虹,宗蓓华.班轮配船模型的改进及其在航运联盟箱位租用中的应用[J].交通运输系统工程与信息,2008,8(3):120-125.[CHEN J H,ZHEN H,ZONG B H.Improved vessel allocation model of liner shipping and its application for slot chartering under shipping alliance[J].Journal of Transportation Systems Engineering and Information Technology,2008,8(3):120-125.]

[5]AGARWALR,ERGUN Ö.Network design and allocation mechanisms for carrier alliances in liner shipping[J].Operations Research,2010,58(6):1726-1742.

[6]FRANSOO J C,LEE C Y.The critical role of ocean container transport in global supply chain performance[J].Production and Operations Management,2013,22(2):253-268.

[7]PAROLA F,SATTA G,PANAYIDES P M.Corporate strategies and profitability of maritime logistics firms[J].Maritime Economics&Logistics,2015,17(1):52-78.

[8]CHEN J,LIU X,ZHANG X,et al.Optimal bilateral cooperative slot allocation for two liner carriers under a co-chartering agreement[J].The Journal of Navigation,2017,70(5):1170-1182.

[9]杨楠.空箱调运的随机机会约束规划模型[J].科技信息,2011(27):I0133-I0133.[YANG N.A stochastic chance constrained programming model for empty container transferring[J].Science and Technology Information,2011(27):I0133-I0133.]

[10]朱萧篥,夏倩.需求随机条件下运输问题的机会约束规划模型研究[J].交通科技与经济,2015,17(2):66-68.[ZHU X L,XIA Q.Study on chance constrained programming model of transportation problem under stochastic demand[J].Technology and Economy in Areas of Communications,2015,17(2):66-68.]

[11]陈继红,胡志华,何新华,等.集装箱班轮联营系统协同测度方法与实证[J].交通运输系统工程与信息,2013,13(6):112-119.[CHEN J H,HU Z H,HE X H,etal.Synergy evaluation method and empirical application for joint-service system of containerized liner shipping[J].Journal of Transportation Systems Engineering and Information Technology,2013,13(6):112-119.]