钢板夹钢管组合板弯曲变形与最大承载力

周竞洋， 夏志成， 张建亮， 孔新立， 刘长财

(1. 陆军工程大学 国防工程学院， 江苏 南京 210007； 2. 宁波市甬泰人防技术咨询有限公司, 浙江 宁波 315016)

近年来，全球恐怖爆炸袭击事件不断增多，已对社会安定和建筑物安全构成重大威胁。为了有效减轻爆炸产生的危害，在建筑物及构筑物前设置防爆组合板[1]，可快速提升建筑物及构筑物的防护能力，有效保障人员的生命安全。

圆钢管材料[2～7]相比其他型钢材料具有优异的受力性能和广泛的使用价值，因而常常用于公路隔离带、石油化工管道和海洋平台支架等重要结构物[8]上。沈国辉等[9]对带加劲肋十字型钢管节点进行了试验和模拟研究，并进一步分析贯穿后的加劲肋对承载力的影响。郭咏华等[10]采用试验和模拟相结合的方法，对高强钢管的稳定性进行了研究，并给出了受压稳定系数计算公式。金霞等[11]基于钢管弯曲变形理论，建立了钢管弯曲部分外侧和内侧壁厚变化的理论公式。汪玉祥等[12]对钢管弯曲变形的影响因素进行了分析，提出了两种减少变形的方法。Xia等[13]对钢板夹钢管组合板进行了接触爆炸和非接触爆炸试验研究。

当前对单根钢管及钢管桁架的力学性能研究较多，对钢板夹钢管组合板力学性能研究较少。防护板材是防爆墙的基本组成构件，其性能好坏将直接影响防爆墙的防护性能。因此本文拟对钢板夹钢管组合板进行抗弯试验、理论分析和数值模拟研究，为防爆墙基本防护板材的结构设计提供基础依据。

1 试验概况

1.1 试验原材料及构件制作

试验钢板采用马鞍山钢铁股份有限公司生产的Q235B热轧钢板，厚度为4.5 mm。钢管采用临沂正阳管业有限公司生产的输送流体用无缝钢管，外径为89 mm，内径为79 mm，壁厚为5 mm。钢板和钢管的材料参数实测值如表1，2所示。

试验组合板共有3块，整体尺寸为长×宽×高=1200 mm×454 mm×98 mm。组合板由上下钢板、两边侧板以及中间钢管组成，截面示意图和实物图见图1。组合板拼装顺序为先将钢管与上下钢板进行焊接连接，然后再将两边侧板与上下钢板和钢管进行焊接。焊接时，沿组合板跨度方向每隔100 mm有一个长约35 mm的角焊缝。

表1 钢板材料参数

表2 钢管材料参数

图1 组合板截面和实物/mm

1.2 试验加载及量测

图2为试验加载量测示意图。试验采用单点加载，利用分配梁分配集中荷载。P为压头作用力，组合板跨度L=1100 mm，压头(分配梁)宽度为160 mm，两端支承外伸长度H=50 mm，两端支座分别采用直径为50 mm的钢棒和高度为50 mm的三角形钢棒。在加载过程中，压头和支座均视为刚性，即假设不发生任何弹性变形和塑性变形。压力传感器沿组合板跨中短边方向三等分点处各布置一个。将9个位移计分别放置在组合板两边支座和跨中位置，沿宽度方向均匀放置3个位移计，用以量测两支座处的沉降及跨中挠度，挠度值由LVDT直线位移传感器收集。组合板跨中实际挠度值可用跨中挠度值减去两支座沉降位移的平均值表示，记为δ。

图2 试验加载量测示意

图3为组合板准静态加载现场。试验加载过程为试验前准备、预加载和正式加载三个阶段。

图3 准静态加载现场

在试验前准备阶段，首先对组合板的尺寸进行仔细复核，确保没有初始变形。然后将位移计、静态应变箱和数据采集仪等测量记录设备安装到位，并确保压力传感器、千斤顶和组合板三者中心在一条直线上。

预加载分3级进行，每级取标准荷载的10%，然后分级卸载。为防止构件在预加载时产生塑性变形，预加载的荷载不超过组合板屈服荷载计算值的20%。

正式加载时，在达到估算屈服荷载之前，每级加载值约为极限荷载的10%。当所加荷载达到估算屈服荷载的90%时，为准确起见，每级加载值改为屈服荷载的5%。待达到屈服荷载后，每级加载值仍按极限荷载的10%进行加载。当所加荷载达到估算极限荷载的90%时，每级加载值再次改为极限荷载值的5%进行加载。

当组合板承载力达到最大承载力时，即认为组合板已经失效。为了进一步分析组合板加载失效后的变形和P-δ曲线变化趋势，当加载达到最大承载力时，并不会立刻停止加载，而是继续加载一段时间。

2 试验结果与分析

图4为组合板试验P-δ曲线[13]，三种组合板的最大承载力依次为325.5，374.9，433.9 kN。由图4可知，钢管数量越多，承载力越大。密排钢管组合板承载力提升量优于间排钢管组合板，主要原因在于密排钢管组合板的钢管为连续排布，连续排布的钢管相互接触，增加了单根钢管的约束，间接提高了钢管的抗失稳能力[14]。

图4 试验P-δ曲线

图5～7分别给出了三种组合板加载失效过程。对比可知，组合板加载变形破坏首先从焊缝开裂开始，其次是压头作用处上钢板的局部屈曲以及钢管局部压扁，当组合板达到最大承载力时，即表示组合板已经失效破坏。在压头作用处，钢板和钢管发生较为严重的局部塑性变形，支座两端的钢管被压扁现象不明显，五钢管组合板焊缝开裂情况要明显好于三钢管组合板和四钢管组合板焊缝开裂情况，表明钢管连续分布的结构形式有利于避免焊缝过早开裂。

图5 三钢管组合板失效过程

图6 四钢管组合板失效过程

图7 五钢管组合板失效过程

3 最大承载力理论公式

图8为假设的组合板失效模型。由图8可知，组合板在加载过程中，δ近似表示加载压头下降位移，各部分做功表现为：压头做功为W1；上钢板在弯曲过程中产生两个塑性铰，并通过塑性铰转动做功为W2；下钢板在一定长度范围内发生弯曲与拉伸，其中弯曲做功为W3，拉伸做功为W4；钢管在弯曲过程中，近似假设发生弯曲与拉伸，其中弯曲做功为W5，拉伸做功为W6；侧板随下钢板弯曲做功为W7。考虑能量平衡，则有：

W1=W2+W3+W4+W5+W6+W7

(1)

图8 组合板理论失效模型

压头做功W1为：

W1=Pδ

(2)

式中：P为压头反力；δ为压头下降的位移。

上钢板塑性铰做功W2为：

(3)

(4)

(5)

式中：Mp为上钢板塑性铰弯矩；b为上、下钢板的宽度；t为钢板的厚度；σby为钢板屈服强度；L为组合板的跨度；θ为组合板一侧转动的角度。

下钢板弯曲做功W3为：

(6)

(7)

式中：Mxgb为下钢板弯矩；r为钢管的内径。

由于下钢板跨中一定长度发生近似圆弧的弯曲，由图8组合板各部分几何关系可知：

(8)

(9)

u+2t+R=e

(10)

2eθ=s

(11)

式中：k为弯曲后两侧上钢板延长线的交点到一侧下钢板弯终点与圆心连线的垂线距离；u为两端上钢板平直段到圆心的垂线距离；i为压头两端到一侧下钢板弯终点与圆心连线的垂线距离；t为钢板厚度；R为钢管内径，e为下钢板弯曲圆弧的半径；s为下钢板弯曲圆弧长度。

由式(8)～(11)可得下钢板拉伸长度Δ为：

(12)

下钢板拉伸做功W4为：

(13)

钢管弯曲做功W5为：

(14)

(15)

(16)

式中：Wx为弯曲截面系数；Mgg为单根钢管的弯矩；n为钢管的数量；R为钢管外径；σgy为钢管屈服强度。

钢管拉伸做功W6为：

(17)

(18)

侧板弯曲做功W7为：

(19)

(20)

式中：Mcb为侧板弯矩。

将各部分做功的具体表达式带入式(1)，可得组合板理论最大承载力P为：

(21)

基于式(21)可以计算得出组合板的最大承载力理论值。表3给出了三种组合板最大承载力理论值与试验值。由表3可知，三种组合板理论值与试验值的误差分别为5.90%，3.65%，-0.32%，表明建立的理论最大承载力公式可以较好地预测组合板的最大承载力。由假设的理论模型可知，推导的最大承载力公式适用于上下钢板厚度相同的对称组合板形式。

表3 最大承载力理论值与试验值

4 有限元模拟分析

4.1 有限元模型及材料参数

由于组合板为对称模型，所以利用ABAQUS/CAE创建组合板的四分之一模型，模型尺寸与试验尺寸完全相同。创建部件时，钢板和钢管均采用Explicit单元库中三维实体单元C3D8R，加载压头采用离散刚体单元R3D4，材料参数取自表1,2。为方便起见，加载压头模型改为平面建模，组合板两端支座用相应约束代替。钢板及钢管均采用理想刚塑性模型。设置分析步时，通过定义场输出和历史输出，可以得到组合板吸能、跨中挠度和承载力等基础数据。通过定义绑定约束来模拟钢板和钢管之间的焊接作用。分析采用ABAQUS/Explicit模块，选择动力-显式。钢管和钢板之间的接触设为通用接触，切向摩擦系数为0.25，法向为硬接触。为了保证模拟精度以及网格均匀对称，划分网格时将网格尺寸控制在4mm以内。钢管网格划分技术选择扫略-中性轴算法，以避免网格畸形，从而影响计算时间和模拟精度。

4.2 试验模拟与验证分析

对原试验进行模拟分析，模拟和试验的P-δ曲线见图9。由图9可知，模拟曲线与试验曲线吻合较好。表4给出了组合板最大承载力模拟值与试验值。三种组合板最大承载力模拟值与试验值误差分别为-1.47%，-0.56%，1.77%，表明基于上述材料参数和数值模型可以较好地模拟原试验。图10给出了组合板的云图。由图10可知，压头作用处的钢管和钢板应力最大，且压头作用处的钢板局部屈曲和钢管局部压扁现象与试验加载失效过程吻合较好。

图9 试验与模拟的P-δ曲线

图10 三种组合板云图

编号试验值/kN模拟值/kN误差/%G3325.5320.7-1.47G4374.9372.8-0.56G5433.9441.61.77

4.3 组合板最大承载力优化分析

组合板最大承载力优化方案主要包括：增强材料性能、增加钢板厚度、增加钢管壁厚和增加钢管数量。在上述方案中，增强材料性能在文中不作讨论，而增加钢管数量，试验部分已经讨论，故不再赘述。下面重点讨论增加钢板厚度和增加钢管壁厚对组合板最大承载力的影响。为避免对钢管数量的重复讨论，故优化方案均在四钢管组合板基础上进行讨论。表5给出了组合板模拟尺寸与编号。

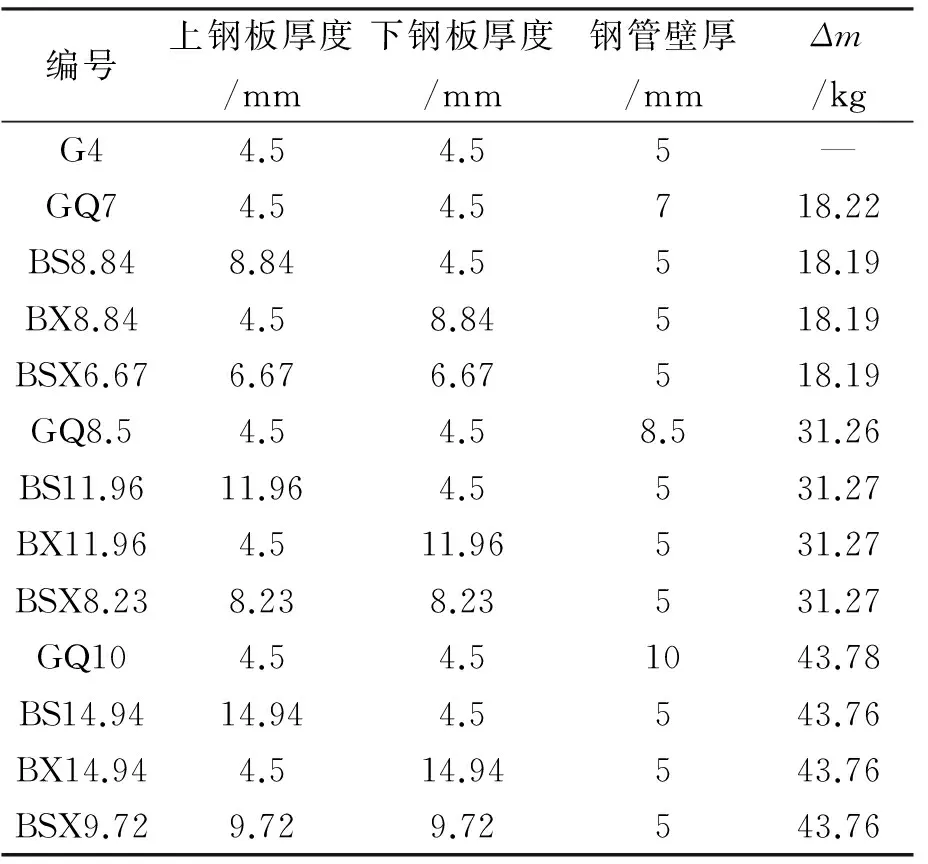
表5 组合板尺寸与编号

注：Δm为组合板增加的重量。GQ7表示四根钢管壁厚同时变为7mm；BS8.84表示仅上钢板厚度变为8.84mm；BX8.84表示仅下钢板厚度变为8.84mm；BSX6.67表示上下钢板厚度同时变为6.67mm；其余编号含义以此类推，不再赘述

4.3.1 最大承载力理论值与模拟值

由于推导的组合板最大承载力理论公式仅适用于上下钢板厚度相等的对称结构形式，因此只对增加钢管壁厚和同时增加上下钢板厚度两种优化方案进行对比分析。表6给出了组合板最大承载力理论值与模拟值。由表6可知，钢管壁厚越大，组合板最大承载力理论值与模拟值的误差也越大，表明推导的组合板最大承载力公式更适合壁厚较小的钢管。上下钢板厚度越大，组合板最大承载力理论值与模拟值的误差先减小后增大，但误差均控制在10%以内，且BSX8.23最大承载力误差仅为0.01，表明推导的组合板最大承载力公式可以较好预测同时增加上下钢板厚度优化方案的最大承载力，具有较高的精度。

表6 最大承载力理论值与模拟值

4.3.2 最大承载力优化方案

图11给出了表4模拟工况的最大承载力。由图11可知，随着用钢量的增加，最大承载力分别出现在AB段和BC段。当用钢量增加较少时，增加上钢板厚度，可使组合板最大承载力达到最大，主要原因在于初始组合板部件厚度较小，当增加上钢板厚度后，使上钢板不至于过早发生塑性铰屈服而失效，从而提高了组合板的整体抗力。当用钢量增加较大时，同时增加上下钢板厚度，可使组合板最大承载力达到最大，主要原因在于同时增加上下钢板厚度将使组合板截面惯性矩达到最大，下钢板和钢管得到充分变形，从而提高了组合板的整体抗力。

图11 模拟工况最大承载力

5 结 论

通过试验研究、理论分析和数值模拟，得到以下结论：

(1)钢管数量越多，组合板抗弯承载力越大。变形失效前，往往先出现焊缝开裂、上钢板局部屈曲和芯层钢管局部压扁等现象。

(2)基于假设的理论失效模型和能量原理，推导的理论最大承载力公式可以较好地预测试验结果和模拟结果，可以为上下面板厚度相同的对称组合板承载力设计提供理论依据。相比增加钢管壁厚优化方案，该公式对同时增加上下钢板厚度优化方案承载力预测精度总体更高。

(3)模拟结果可以较好预测试验结果。加载过程中，压头作用处的钢板和钢管局部变形最严重，产生的应力最大。

(4)当用钢量增加较少时，增加上钢板厚度对组合板最大承载力的提升最为有效。当用钢量增加较大时，同时增加上下钢板厚度对组合板最大承载力的提升最为有效。

[1]XiangXM,LuG,WangZH.Quasi-staticbendingbehaviorofsandwichbeamswiththn-walledtubesascore[J].InternationalJournalofMechanicalSciences, 2015, 103: 55-62.

[2]LiuY,DayML.Bendingcollapseofthin-walledcirculartubesandcomputationalapplication[J].Thin-WalledStructures, 2008, 46(4): 442-450.

[3] 路国运, 秦庆华, 雷建平, 等. 厚壁压力管道侧向冲击破坏的实验研究[J]. 实验力学, 2004, 19(3): 353-358.

[4] 秦庆华, 路国运, 雷建平, 等. 薄壁圆管侧向冲击动力响应的仿真分析[J]. 太原理工大学学报, 2003, 34(5): 513-516.

[5]AarønsA,NilssonH,NeumannN.Dynamicresponseofsteelpiperackstructuressubjectedtoexplosionloads[J].SteelConstruction, 2015, 8(3): 162-166.

[6]HuoS,ChaoY,DaiG,etal.FieldTestResearchofinclinedlarge-scalesteelpipepilefoundationforoffshorewindfarms[J].JournalofCoastalResearch, 2015, 73(s1): 132-138.

[7] 王 蕊, 秦庆华, 程国强, 等. 金属圆管在轴向冲击力作用下的破坏基理[J]. 太原理工大学学报, 2004, 35(4): 392-395.

[8] Guo L, Yang S, Jiao H. Behavior of thin-walled circular hollow section tubes subjected to bending[J]. Thin-Walled Structures, 2013, 73: 281-289.

[9] 沈国辉, 陈 震, 郭 勇, 等. 带加劲肋十字型钢管节点支管轴压的承载力研究[J]. 工程力学, 2013, 30(9): 70-75.

[10]郭咏华, 李晓彦, 张 斌, 等. 高强钢轴心受压钢管整体稳定性承载力试验研究及数值分析[J]. 工程力学, 30(8): 111-118.

[11]金 霞, 李 强. 薄壁管材弯曲变形理论分析[J]. 机械研究与应用, 2007, 20(5): 30-31.

[12]汪玉祥, 康志军. 管材弯曲的变形研究[J]. 淮阴工学院学报, 2002, 11(3): 27-29.

[13]Xia Z, Wang X, Fan H, et al. Blast resistance of metallic tube-core sandwich panels[J]. Internation Journal of Impact Engineering, 2016, 97: 10-28.

[14]顾红军, 方维凤, 郭胜鹏. 薄壁钢管动力全屈曲变形分析及计算[M]. 北京: 国防工业出版社, 2009.

[15]Jones N. Energy-absorbing effectiveness factor[J]. International Journal of Impact Engineering, 2010, 37(6): 754-765.