基于实际车流的在役桥梁承载力动态评定方法
2018-03-01杜延昭王云燕
梁 栋, 董 婉, 杜延昭, 王云燕
(1. 河北工业大学 a. 土木与交通学院; b. 河北省土木工程技术研究中心, 天津 300401;2. 石家庄市京昆高速公路石太管理处, 河北 石家庄 050073)
近年来,随着桥梁建设增多,交通量和重型汽车数量快速增长,很多桥梁长期处于超载超限的服役状态,不断发生垮桥、损桥事故,这不仅给人民生命财产带来了巨大损失,也造成了恶劣的社会影响。例如,2011年5月29日,建成于1989年的长春市伊通河荣光大桥由于车辆超载,导致大桥桥面发生塌陷(图1),货车坠入河中,两人不同程度的受伤;2011年7月14日,武夷山公馆大桥由于车辆严重超载超限,导致大桥北端发生坍塌事故,一辆旅游大巴车坠入桥下,造成1人死亡,22人受伤;2011年7月19日,北京市宝山寺白河桥由于货车严重超载,导致桥梁4孔全部坍塌(图2)[1]。

图1 伊通河荣光大桥桥面塌陷

图2 宝山寺白河桥4孔全部坍塌
究其原因,主要是桥梁的实际通行情况与设计条件存在较大差异;同时,桥梁承载力评定一般是依据设计荷载通过荷载试验进行。由此带来的主要问题有:一方面,使用设计荷载作为标准开展荷载试验,和桥梁实际通行状况相去甚远,而且目前桥梁超载超限问题相当严重,使用设计荷载进行试验在一定程度上并没有太大的意义;另一方面,使用静力性能去评定桥梁的工作性能,这和桥梁在汽车荷载作用下的实际工作状态也不相符。因此,有必要寻求一种接近桥梁实际运行状态的动态评定方法,来对桥梁进行承载力评定。
为解决上述问题,很多学者开展了卓有成效的研究工作。谭学民、钟晓林[2]在原设计承载能力基础上,以各项因素折减系数折算求出桥梁现有承载能力,但由于各经验系数的研究工作做的不够充分,系数较难确定;长安大学贺栓海等[3]通过试验建立结构动刚度与静刚度之间的关系,计算结构名义配筋率并以此建立模型分析结构承载力;胡大琳等[4]通过对钢筋混凝土构件不同阶段的频率、阻尼比以及振型进行分析,回归得出结构模态参数与承载力之间的关系对结构承载力进行评估;宗周红等[5]根据实测动力特性指标值,得出反映结构实际受力状态的有限元模型,以有限元为基础分析结构承载能力;孙晓燕等[6]通过对超载作用下结构破损前后的动力参数进行回归分析,建立频率和阻尼比等模态参数与承载力之间的关系,并以此来评定结构承载力;长安大学孙鹏旭[7]分别利用等代荷载法和实际荷载验算法验算超限车辆过桥承载力,以及中小跨径桥梁承载能力。指出等代荷载法适宜在时间紧、任务重的情况下,验算桥梁极限承载力,而实际荷载验算法相对精确,但专业性较强,一般人员尤其是养护人员很难操作。
上述学者的研究中,动力参数的获取受环境影响比较大,只有提高试验手段和方法,才能取得比较精确的数据,不同桥型不同病害等因素对结构动力参数的影响关系还需要大量桥梁的样本数据作为补充。而且目前超载试验资料较少,基于动态评估方法的超载试验更加罕见,因此超载损伤导致的动力参数变化只能定性描述。
1 基于实际车流的在役桥梁承载力动态评定方法
为弥补上述研究的不足,对桥梁实际运行状态下的承载能力进行更为精确的评定,本文在对在役桥梁实际通行状态调查的基础上,提出以桥梁实际工作状态下的荷载等级为标准,选用跑车试验,利用动挠度作为评价指标来评定其承载力。
基于实际车流的在役桥梁承载力动态评定方法的具体步骤如下:(1)对在役试验桥梁进行实际车流的调查,包括车辆数、车辆类型、车速等;(2) 依据调查数据,利用自编的随机车流程序RCAR,生成随机车流;(3) 用有限元软件Ansys建立试验桥梁的模型,分析随机车流下桥梁的挠度指标,将此挠度指标作为桥梁实际工作状态下的标准荷载等级;(4) 依据新确定的标准荷载等级以及荷载试验效率系数,在桥梁模型中进行车辆数和车速的组合验算,并最终确定试验所需要的车辆数和车速;(5)进行跑车试验,测量试验桥梁的动挠度指标;(6)将试验结果与(4)中的理论值进行比较分析,计算校验系数,评定试验桥梁的承载力是否满足要求。
2 动态评定方法的试验验证
2.1 试验准备
为了说明上面提出的跑车试验评定桥梁承载力的可行性,进行室内试验加以验证。本文以某高速公路实桥为背景,按10∶1缩尺比例设计了一简支梁模型,桥梁跨径300 cm,桥面总宽150 cm,设为单向四车道,车道荷载取为Pk=0.96 kN,qk=0.06 kN/m,限速50 mm/s。
试验加载车采用重物和轮子模拟,绳子一端系在模拟装置上,另一端系在电机上,用电机牵引绳子拉着重物前进模拟牵引装置。轮距15.5 cm,加载车之间的安全距离为9.5 cm,设护栏宽3.0 cm,车轮与护栏间的安全距离为4.5 cm。全桥采用有机玻璃板粘结而成的等截面小箱梁结构,横向一共四片梁,结构细部尺寸如图 3所示。

图3 横断面细部尺寸/cm
2.2 试验步骤
桥梁横断面从左面开始,依次为1#梁、2#梁、3#梁、4#梁。在1#梁和2#梁梁底架设激光位移计,编号a,b。
试验开始,距护栏4.5 cm处,第一车道上第1辆加载车以50 mm/s的速度匀速驶过桥跨结构;距第一辆加载车9.5 cm的安全距离处,两车同时以50 mm/s的速度匀速驶过桥跨结构;依次增加直到达到设计车道数,也就是4辆加载车同时行驶。车辆行驶过程中,采集激光位移计a,b的数值,试验加载如图 4所示。

图4 试验加载
2.3 有限元模型
依据试验梁参数,用Ansys有限元软件建模,得到跑车试验下的理论值。模型如图5所示。

图5 有限元模型立面
2.4 试验结果
为了对桥梁模型进行承载力评定,依据试验记录数据得到各梁的实测值,并计算校验系数如表1所示。
分析比较试验结果发现,校验系数h(h=实测值/理论值)在0.60~1.00之间,均符合规范[8]要求,说明试验梁的承载力满足要求,用跑车试验评定桥梁的承载力是可行的。

表1 试验结果
3 实际通行状态下公路桥梁的动挠度计算
3.1 分析方法
本文选择某一重载交通区进行交通情况的调查,根据调查数据,用数学方法和软件模拟出实际运行状态下的车流,然后运用有限元程序Ansys进行建模,分析实际车流下桥梁的动挠度,作为桥梁实际工作状态下的标准荷载等级。
根据前人研究的结果[9~11],认为车的质量和速度是影响桥梁动态测试的重要因素。以上述计算结果作为标准荷载,同样建模分析比较相应动挠度指标下跑车试验需要的车辆数和车速,然后进行跑车试验,来评定当前实际工作状态下的桥梁承载力。
3.2 实际通行车流的荷载表达
3.2.1 重载情况调查
本文选择某一重载交通区进行实际通行状态下车辆数据的调查,调查情况见表2(节选部分调查数据)。

表2 某重载交通区车辆数据调查
3.2.2 车辆参数的确定
实际通行状态下,桥上行驶的车辆参数具有很大随机性,这种随机性可以由概率论中连续型分布函数为依据来进行描述。本文选择车型、车头间距、车重、车速来描述行进中的车辆。
(1)车型的确定
根据有关调查数据显示[12],目前我国主要有5种车辆模型,各种车辆模型参数详见表3。
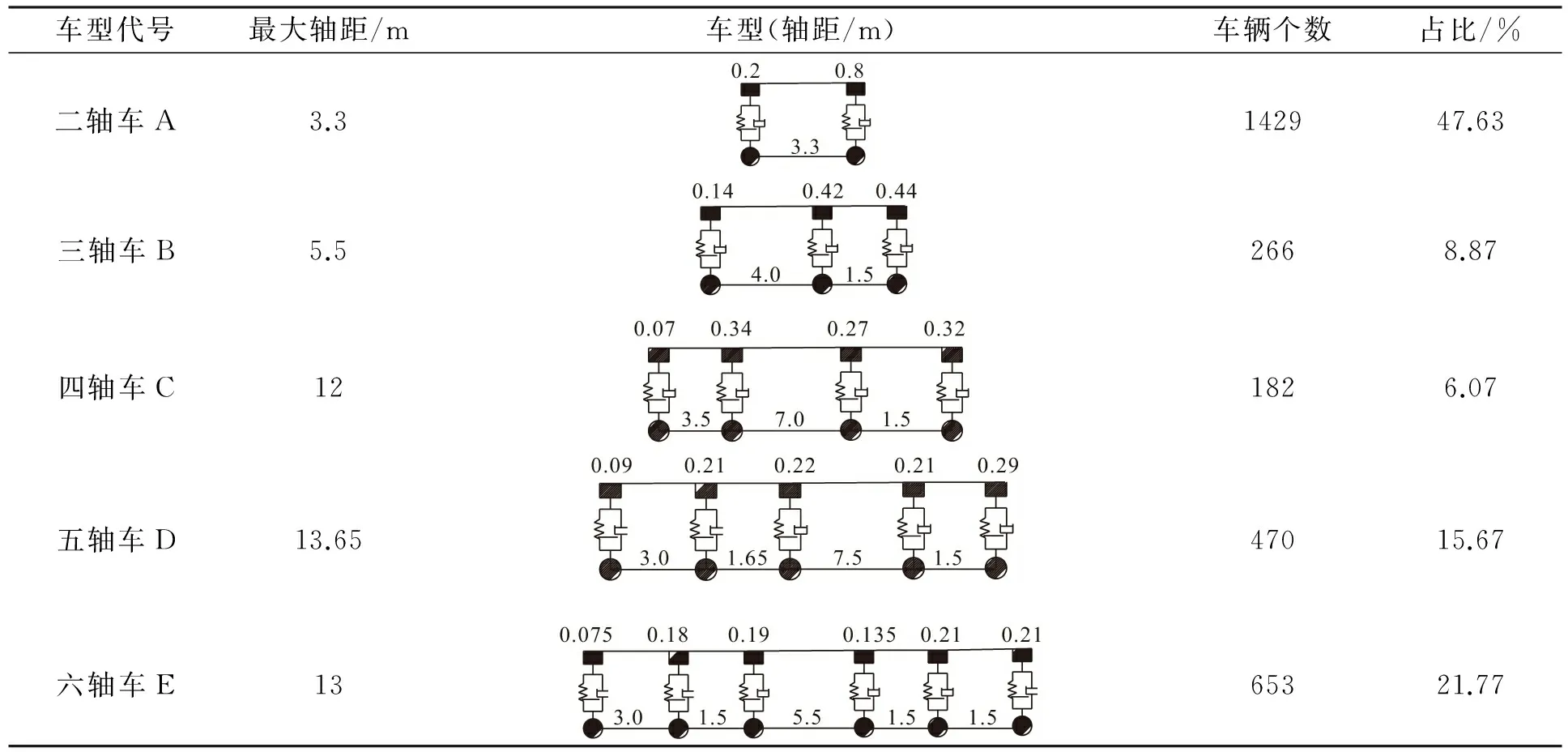
表3 各种车辆模型参数
(2)车头间距的确定
很多学者对车头间距做过一定的研究[13,14],发现车头间距服从正态分布或对数正态分布。本文在前人研究的基础上,做如下规定:在桥上出现堵车情况时,车头间距可以达到最小值,将这个最小值近似定为车辆前、后间轴距,其车头间距上限值规定为桥梁的计算跨径;然后利用M-C方法生成一组基于车头间距最小值、最大值之间的正态分布数据,进而得到模拟车头间距d的频率分布图。例如,对于最小车间距3.3 m,桥梁计算跨径30 m,样本容量为500的正态分布随机序列,模拟得到的车头间距样本分布直方图如图6所示(图中:N为样本容量;μ为正态分布的平均值;σ2为正态分布的方差)。

图6 车头间距样本分布直方图
(3)车重的确定
国内外很多学者对车重做过一定的调查研究[11],发现每种车型都有其具体的车重范围,A型车符合正态分布,B,C,D,E型车符合双峰正态分布,具体分布参数见表4。

表4 车重分布参数
注:p为分布参数的概率
(4)车速的确定
本文将所统计的现场汽车运行状态分为两种,即密集运行和一般运行状态。认为密集运行时,时间间隔在3 s以下,包括堵车状态;一般运行时,时间间隔在3 s及以上。并在前人研究的基础上,将车队行驶速度简化为以下式子:v=1.2dkm/h(d为平均车头间距)。
3.2.3 实际车流模拟
以上述调查数据和统计分析为基础,对车型、车头间距和车重进行分布拟合,利用M-C法生成各自所对应的随机数[15,16],并以车辆的轴重、轴距分配模型,以此形成接近实际通行状况下的车流数据。基于上述原理,利用MATLAB语言编制随机车流程序RCAR,其计算流程如图7所示,生成的随机车流如图 8所示(节选生成的30辆车区段模型),图中A~E代表车型,符号附近的数据代表车辆行驶速度。

图7 RCAR计算流程

图8 随机车流示意
3.3 实际通行车流下的动挠度
为了确定实际通行状态下桥梁的荷载等级,选择该重载交通区常用的30,40 m的三跨连续梁桥为研究对象分析。运用Ansys软件建立有限元模型[17],选择相同的车速,计算可得相应的动挠度时程曲线(图9,10)。

图9 3×30 m连续梁桥位移时程曲线
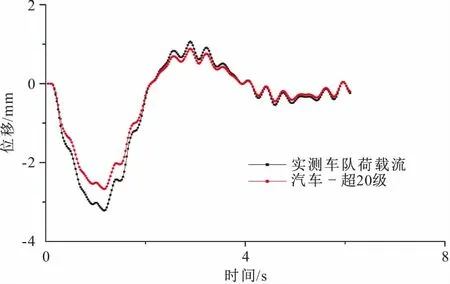
图10 3×40 m连续梁桥位移时程曲线
由上述结果可以看出,仅利用汽车-超20级作为设计荷载进行荷载试验所得到的结果不能反应桥梁的实际工作状态,是偏于不安全的。
4 动态评定实例
为验证本文所提出的实际车流下在役桥梁承载力动态评定方法,选择该地区一简支T梁桥进行承载力评定试验。该桥跨径为11.4 m,设计荷载为公路-I级,设计车道数为2车道,上部结构为4片T梁,桥面宽7+0.75×2+0.1×2 m,梁高为110 cm。为了说明基于实测车流的桥梁动态评定方法的实用性,对该桥进行常规静载对比试验分析。
4.1 基于跑车试验的桥梁承载力评定试验
根据上文的方法步骤,先对该桥进行交通情况的调查,并依据调查数据,确定该桥实际通行状态下的荷载等级。用Ansys建立有限元模型,将此荷载等级加载到模型上,得到跨中截面挠度理论值。
由目前加载车辆的重量和该桥的限速规定,进行车辆数量和车速的组合,分析各个荷载组合下有限元模型的动挠度时程曲线,通过试算,发现选取2×35 t的三轴加载车以平均车速20 km/h行驶时,跨中截面的最大位移值和标准荷载等级引起的理论值最接近,故选择2×35 t的三轴加载车进行试验。
试验依据规范要求,在1和2号梁的梁端及跨中分别布置挠度测点,采用电阻式位移计进行测量。为了准确测量跨中挠度值,去除支座沉降对跨中挠度的影响,在两端支座处也布置位移计,具体挠度测点布置如图11所示。
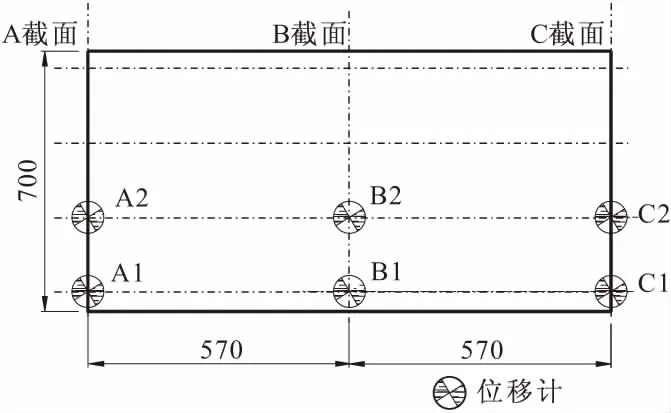
图11 挠度测点布置平面/cm
试验分为两级加载,具体加载车布置方案见图 12,13。

图12 一级加载示意/cm

图13 二级加载示意/cm
4.2 试验结果分析
根据试验结果计算校验系数h如表5所示。

表5 B截面各工况加载等级测试挠度值
分析表中数据发现,校验系数h(h=实测值/理论值)在0.60~1.00之间,符合规范要求,说明试验梁的承载力满足要求。
4.3 常规静力荷载试验
按照规范要求,该桥设计荷载为公路-I级,建立有限元模型,得到跨中截面挠度理论值。按规定计算得到用2×35 t的加载车进行试验,试验过程分两级加载和一次性卸载,一级加载C1车,二级加载C1+C2车,试验加载平面布置如图 14所示。

图14 跨中截面试验加载平面布置/cm
4.3 试验结果对比
各测试点仪器完整记录了加载车从上桥到离桥时段内的时间-挠度曲线,测点B1和B2记录数据见表 6。

表6 B截面各工况加载等级测试挠度值
注:表中u=(yd-yj)/yj
对表中数据进行误差分析和测试时间分析,可得:umax=2.6%<5.0%,说明相对误差在允许范围之内。常规静载试验实测值均小于动载试验实测值,说明静载试验测试值与桥梁结构的实际运行状态有一定的出入,由车桥耦合振动所引起的桥梁结构变形也不能准确反映出来,所以本文提出的基于实测车流的桥梁承载力动态评定方法更加合理,具有一定的现实意义。
5 结 语
本文针对目前桥梁出现的超载超限问题,考虑桥梁实际运营状况,提出了一种基于实际车流的桥梁承载力动态评定方法,并通过室内试验和实桥评定验证了这种方法的可行性。
研究发现:
(1)运用本文提出的方法进行荷载试验,试验校验系数符合公路桥梁承载能力检测评定的规定,说明试验桥梁的承载力是满足要求的;
(2)通过和常规静载试验对比,得到试验实测值大于常规的静载试验,说明试验结果更加接近桥梁的实际运营状况;
(3)试验选择车辆以一定车速从标准车道上驶过,试验流程简单易行,方便快捷,相比静载试验需要将车辆的轮胎准确地加载到桥梁结构的固定位置,节约了大量的时间和人力物力,经济效益明显。
综上,说明本文提出的基于实测车流的桥梁承载力动态评定方法更能反应桥梁的实际运营状况,有一定的实际意义。
[1] 戈 铭, 王 涛. 桥梁坍塌事故的原因分析及其预防措施[J]. 特种结构, 2012, 29(2): 72-75.
[2] 谭学民, 钟晓林. 基于检测的折算系数法评定桥梁承载力研究[J]. 广州建筑, 2008, 36(5): 23 -27.
[3] 贺拴海, 郭 琦, 宋一凡, 等. RC桥梁健康状况及承载能力的动力评估试验[J]. 长安大学学报(自然科学版), 2003, 23(6): 36 -39.
[4] 胡大琳, 王克鸿, 罗 丁. 钢筋混凝土梁桥破损模态分析及承载力评定[J]. 西安公路交通大学学报, 1999, 19(2): 31-35.
[5] 宗周红, 阮 毅, 任伟新. 基于动力的预应力混凝土独塔斜拉桥承载力评估[J]. 铁道学报, 2004, 26(6): 86-94.
[6] 孙晓燕, 黄承逵, 窦玉秋, 等. 考虑超载影响的混凝土简支梁结构动态评估[J]. 水力发电学报, 2005, 24(3): 105-109.
[7] 孙鹏旭. 基于超载运输的在役中小跨径桥梁承载力研究[D]. 西安: 长安大学, 2015.
[8] JTG/T J21-2011, 公路桥梁承载能力检测评定规程[S].
[9] 舒绍云, 施尚伟, 王海城, 等. 桥梁结构性能综合评价方法研究[J]. 建筑结构, 2010, 40(s1): 97-99.
[10]王永平, 陈彦江, 傅金科. 单车荷载下简支梁桥的动力特性和响应的试验研究[J]. 土木工程学报, 1995, (5): 39-47.
[11]史剑发. 简支转连续多片箱梁桥静动载试验研究[D]. 长春: 吉林大学, 2011.
[12]安振源. 基于实桥车辆调查的在役桥梁可靠度研究[D]. 西安: 长安大学, 2010.
[13]王元庆, 李继锐, 周 伟. 道路车间时距分布探讨[J].重庆交通学院学报, 2001, 20(1): 47-49.
[14]罗 霞, 杜进有. 车头间距分布规律的研究[J]. 西南交通大学学报, 2001, (2): 113-116.
[15]杨自强, 魏公毅. 任意分布随机变量抽样的通用算法与程序[J]. 数值计算与计算机应用, 2006, (3): 191-200.
[16]朱晓玲, 姜 浩. 任意概率分布的伪随机数研究和实现[J]. 计算机技术与发展, 2007, 17(12): 116-118.
[17]张 洁. 基于总成结构的重型载货汽车建模与操纵稳定性仿真[D]. 长春: 吉林大学, 2011.
[18]党 栋. 公路桥梁设计荷载及其组合研究[D]. 西安: 长安大学, 2012.
[19]肖志辉, 郭 鑫. 广西全兴高速公路屏山渡湘江大桥荷载试验[J]. 公路与汽运, 2009, (5): 150-153.
[20]谌润水, 胡钊芳. 公路桥梁荷载试验[M]. 北京: 人民交通出版社, 2003.
[21]张宇峰, 段鸿杰, 马志国. 基于准静态荷载试验的梁式桥梁状态快速评定[J]. 现代交通技术, 2009, 6(5): 21-24.
