仿生变刚度关节设计与试验
2018-03-01房立金周生啟
王 颜 房立金 周生啟
(1.东北大学机械工程与自动化学院, 沈阳 110819; 2.东北大学机器人科学与工程学院, 沈阳 110819)
0 引言
随着机器人技术的日益成熟,穿戴式机器人、康复机器人、假肢等以人为中心的机器人应用领域越来越多,使用者与机器人本体接触的物理性人机交互也随之增加[1]。为了提高人机交互的安全性,有多种驱动方式已应用于仿生关节,如智能材料驱动[2-3]、气动人工肌肉驱动[4-5]。此外,电动机驱动的机械式仿生变刚度关节受到许多学者关注,在动力输入与输出之间采用弹性元件连接,通过改变弹性元件的受力形式实现刚度的非线性变化[6],能够从本质上实现人机交互安全性。MACCEPA[7]、NST[8]、FAS[9]中的弹簧变形方向与所受外力的方向呈一定角度,通过预紧弹簧来调节刚度,在平衡位置时仍损耗能量。利用特殊零件的曲面或斜面挤压弹簧也可以产生非线性变刚度特性,如MACCEPA 2.0[10]、PVSA[11],但对零件的轮廓要求较高。在vsaUT-Ⅱ[12]、HDAU[13]和AwAS-Ⅱ[14]中,弹簧力作用点、载荷作用点及支点构成杠杆结构,通过改变外力与弹簧力的力臂比值改变刚度,在平衡位置不必损耗能量,但受力时仅一侧弹簧起作用,刚度随着偏角的增加而持续增大。采用弹簧片的变刚度关节/驱动器大多是通过改变弹簧片有效长度实现变刚度的目的,如VSR-joint[15]、VSJ[16]、ADEA[17]和超弹性材料变刚度关节[18]均采用这种方式调节刚度,在平衡位置不损耗能量,刚度范围与弹簧片长度有关。
本文设计一种仿生变刚度关节,以弹簧片作为弹性元件,并综合考虑关节和电动机的整体布局及输出结构,使关节便于安装,输出架更平稳。对变刚度关节的机构原理和主要功能机构的设计及关节参数进行介绍。基于大挠度变形的椭圆积分方法,对2种弹簧片末端施力结构的刚度特性进行仿真分析,并对样机进行刚度性能试验。
1 变刚度关节原理
变刚度关节通过调节弹簧片的有效长度来实现刚度的改变,其工作原理如图1所示,由中心轴、移动支座、位置支架、输出架及2个弹簧片组成。位置支架和输出架可以绕中心轴旋转。弹簧片一端固定在位置支架上,另一端与载荷作用点相连,而载荷作用点可以在输出杆上的滑槽内移动,位置支架通过弹簧片、载荷作用点与输出架连接。移动支座在位置支架上沿着弹簧片相对或相反移动,来调节移动支座与载荷作用点间的弹簧片有效长度l。载荷作用点与中心轴之间的距离为关节力臂lj,输出架受外力矩τ作用而相对于原位置偏转θj。位置支架的旋转与移动支座的移动分别独立地控制关节的位置和刚度。

图1 变刚度关节原理简图Fig.1 Principle of variable stiffness joint1.中心轴 2.移动支座 3.弹簧片 4.位置支架 5.载荷作用点 6.输出架
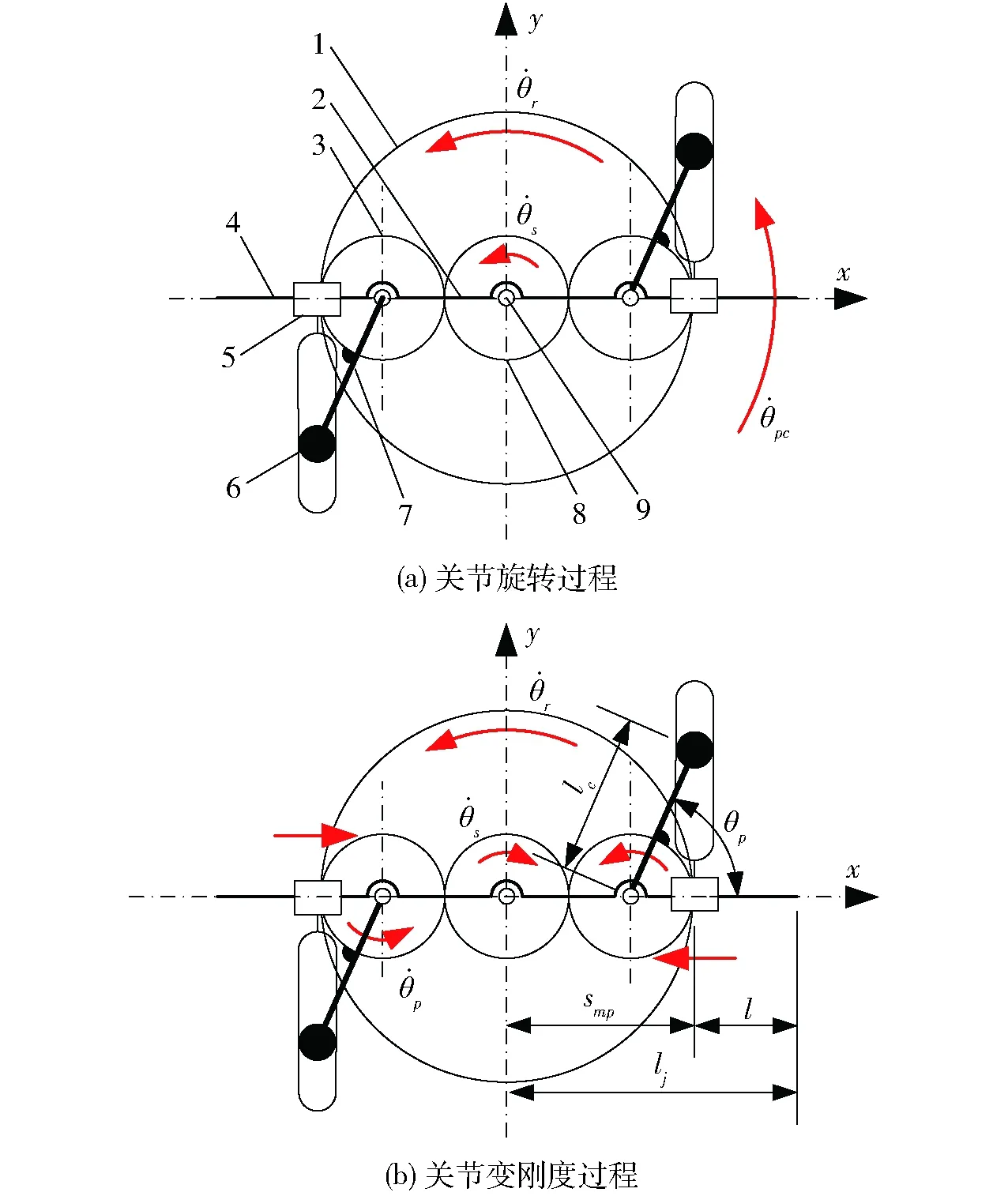
图2 基于差动轮系的变刚度机构的工作原理Fig.2 Working principle of variable stiffness mechanism based on differential gear train1.齿圈 2.行星架 3.行星轮 4.位置支架 5.移动支座 6.销轴 7.曲柄 8.太阳轮 9.中心轴
根据图1的原理,提出了一种基于差动轮系的变刚度机构的设计,其工作原理如图2所示,利用2自由度差动轮系驱动变刚度机构。变刚度机构包括固定在行星架上的位置支架、与行星轮轴相连的曲柄、带有滑槽的移动支座以及一端固定在位置支架上的弹簧片。图2a为关节旋转过程,当太阳轮与齿圈不产生差动,同向同速转动时,行星轮不自转,仅行星架及与其相连的位置支架旋转,转速关系为
(1)

图2b为关节变刚度过程,仅行星轮自转,而行星架不转动,此时太阳轮与齿圈转动方向相反,并且转速关系为
(2)
式中Ns——太阳轮齿数Nr——齿圈齿数
由于曲柄与行星轮相连,当行星轮自转时,曲柄也随之转动,此时,通过曲柄另一端上的销轴拨动移动支座沿位置支架移动,此时,弹簧片有效长度改变,变刚度机构将行星轮的自转变为移动支座的直线移动。2个移动支座相对中心轴作中心对称布置,可以实现同时相向或相反地移动。移动支座与中心轴间的距离为
smp=0.5mNs+0.5mNp+lccosθp
(3)
式中Np——行星轮齿数lc——曲柄长度θp——行星轮转动的角度m——齿轮模数
弹簧片有效长度l为
l=lj-smp
(4)
2 变刚度关节的结构设计
根据变刚度机构的原理,设计了变刚度关节,图3为变刚度关节模型的3D视图,主要的功能机构为动力输入机构、差动轮系和变刚度机构。动力输入机构分为齿圈动力输入机构和太阳轮动力输入机构。齿圈电动机通过齿圈动力输入机构驱动差动轮系中的齿圈,太阳轮电动机通过太阳轮动力输入机构驱动差动轮系中的太阳轮,而齿圈和太阳轮共同驱动行星轮和行星架。变刚度机构中的位置支架固定在行星架上,移动支座通过曲柄和销轴与行星轮轴相连。变刚度机构中的弹簧片通过滑杆与输出架相连,滑杆可以在输出架上的滑槽中滑动。输出架相对于固定支架旋转。

图3 变刚度关节的3D视图Fig.3 3D views of variable stiffness joint1.齿圈动力输入机构 2.太阳轮动力输入机构 3.差动轮系 4.变刚度机构 5.输出架 6.滑杆 7.齿圈电动机 8.太阳轮电动机 9.固定支架
主要功能机构及关键部件如图4所示。基于差动轮系的变刚度机构的具体结构如图4a所示。位置支架如图4b所示,采用H型结构,既满足受力要求,又使结构紧凑。输出架如图4c所示,可绕中心轴转动,是由1个连接件连接2个带有滑槽的构件组成的U型架,U型结构使输出架受力时更稳定,具有较好的承载能力。齿圈动力输入机构和太阳轮动力输入机构均由蜗轮蜗杆、同步带轮及同步带组成,分别如图4d、4e所示,动力输入机构改变了动力传动的方向,使关节易于安装。
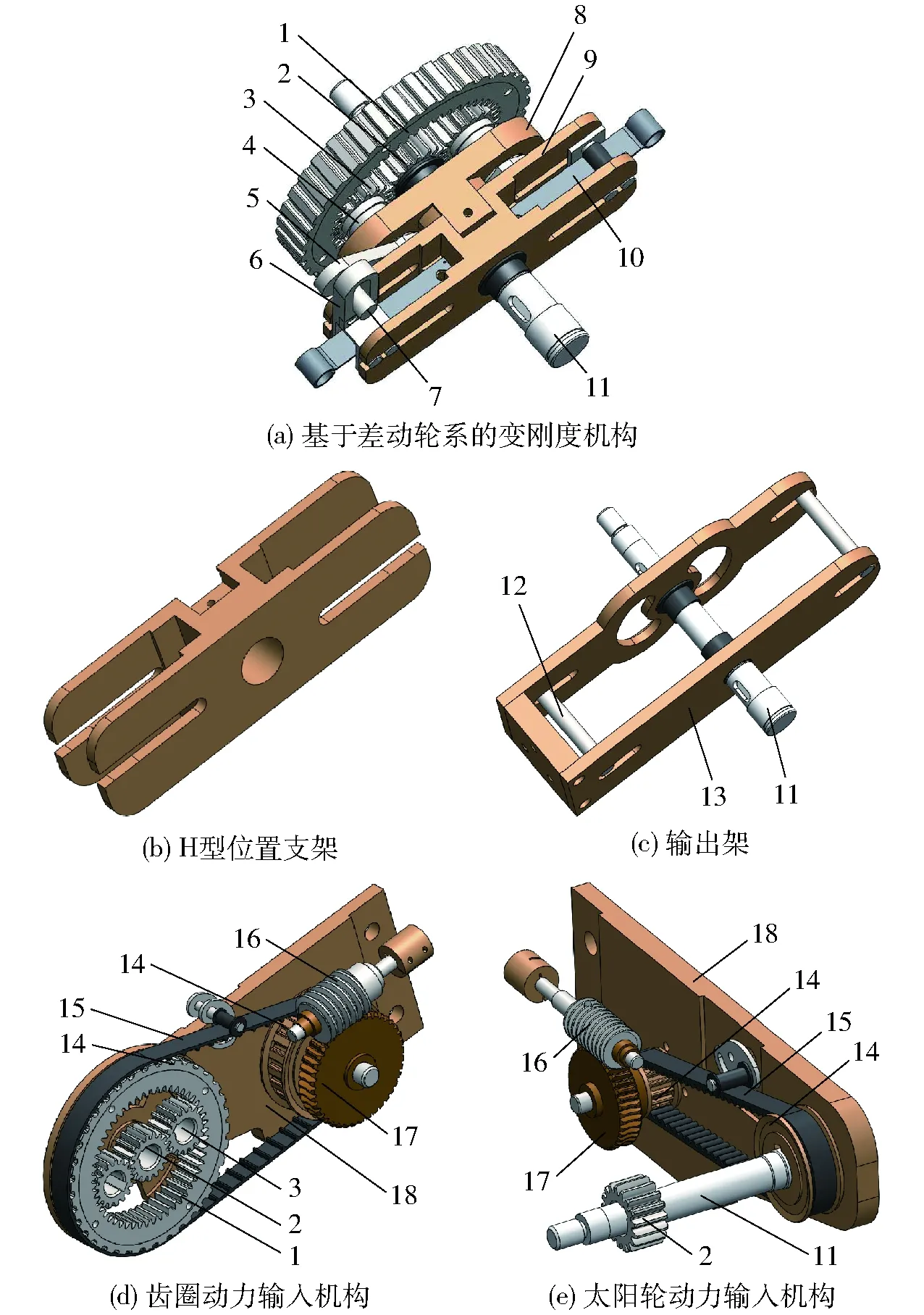
图4 主要功能机构及关键部件Fig.4 Fundamental mechanisms and key components1.齿圈 2.太阳轮 3.行星轮 4.行星轴 5.曲柄 6.移动支座 7.销轴 8.行星架 9.位置支架 10.弹簧片 11.中心轴12.滑杆 13.输出架 14.同步带轮 15.同步带 16.蜗杆 17.蜗轮 18.固定支架
变刚度关节的具体参数如表1所示,弹簧片的相关参数如表2所示。

表1 变刚度关节参数Tab.1 Parameters of variable stiffness joint
3 末端施力结构对关节刚度特性的影响分析
提出的变刚度关节中的弹簧片末端施力结构如图5a所示,作为弹簧片上载荷作用点的滑杆相对输出架移动,该结构中的弹簧片有效长度在关节偏转时不变;而在引言中提到的以弹簧片作为弹性元件的变刚度机构中,常采用的弹簧片末端施力结构如图5b所示,作用于弹簧片上的杆固定在输出架上,即载荷作用点位置不变,该结构中弹簧片有效长度在偏转时会改变,可以将本关节的滑杆固定在输出架来实现这种末端施力结构。

表2 弹簧片参数Tab.2 Parameters of leaf springs

图5 2种弹簧片末端施力结构Fig.5 Two structures to exert external force on end of leaf spring1.移动支座 2.弹簧片 3.滑杆 4.滑槽 5.输出架 6.固定杆
根据图5中2种弹簧片末端施力结构,一侧弹簧片受力而产生的大挠度变形如图6所示,旋转中心为O点,移动支座为O′点,载荷作用点为B点。不考虑摩擦力,当关节受到外力矩τ偏转时,弹簧片上受到外力F。以O′点为坐标系原点,弹簧片在B点的转角为θB,挠度为ω,水平方向的位移为δ。

图6 一侧弹簧片的大挠度变形示意图Fig.6 Sketch of large deflection of a leaf spring
根据图6a中的受力分析,任意一点的弯矩M与曲率的关系为
(5)
式中E——弹簧片弹性模量I——弹簧片惯性矩
根据图6b中的受力分析,任意一点的弯矩M与曲率的关系为
(6)
基于悬臂梁的大挠度变形的椭圆积分方法[19-21]来求解式(5)、(6),第一类和第二类不完全椭圆积分分别为
式中φ——幅度k——模数(-1≤k≤1)
当φ=π/2时,则为第1类和第2类完全椭圆积分,分别记为F(k)和E(k)。图6a一侧输出架所受的外力矩可表示为
(7)
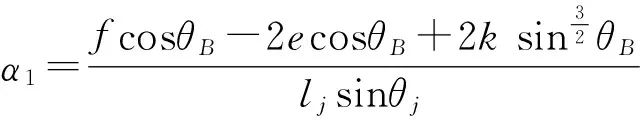

图6b一侧输出架所受的外力矩可表示为
(8)
其中
α2=f/l
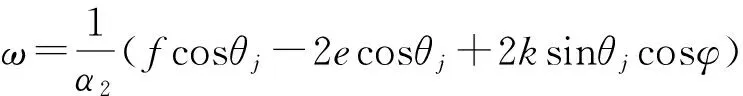
关节刚度kj为
(9)
式中n——弹簧片个数,取2
以一侧弹簧片为例,进行仿真分析,外力矩τ与关节偏角θj的关系如图7所示,关节刚度kj与关节偏角θj的关系如图8所示。对于图5a中的弹簧片末端施力结构,kj随着θj的增大而增大,可以应用在持续提供高刚度的工作场合;对于图5b中的弹簧片末端施力结构,kj随着θj的增大而减小,可以提高碰撞安全性。仿真结果表明,末端结构对关节偏转时的刚度变化有较大影响。
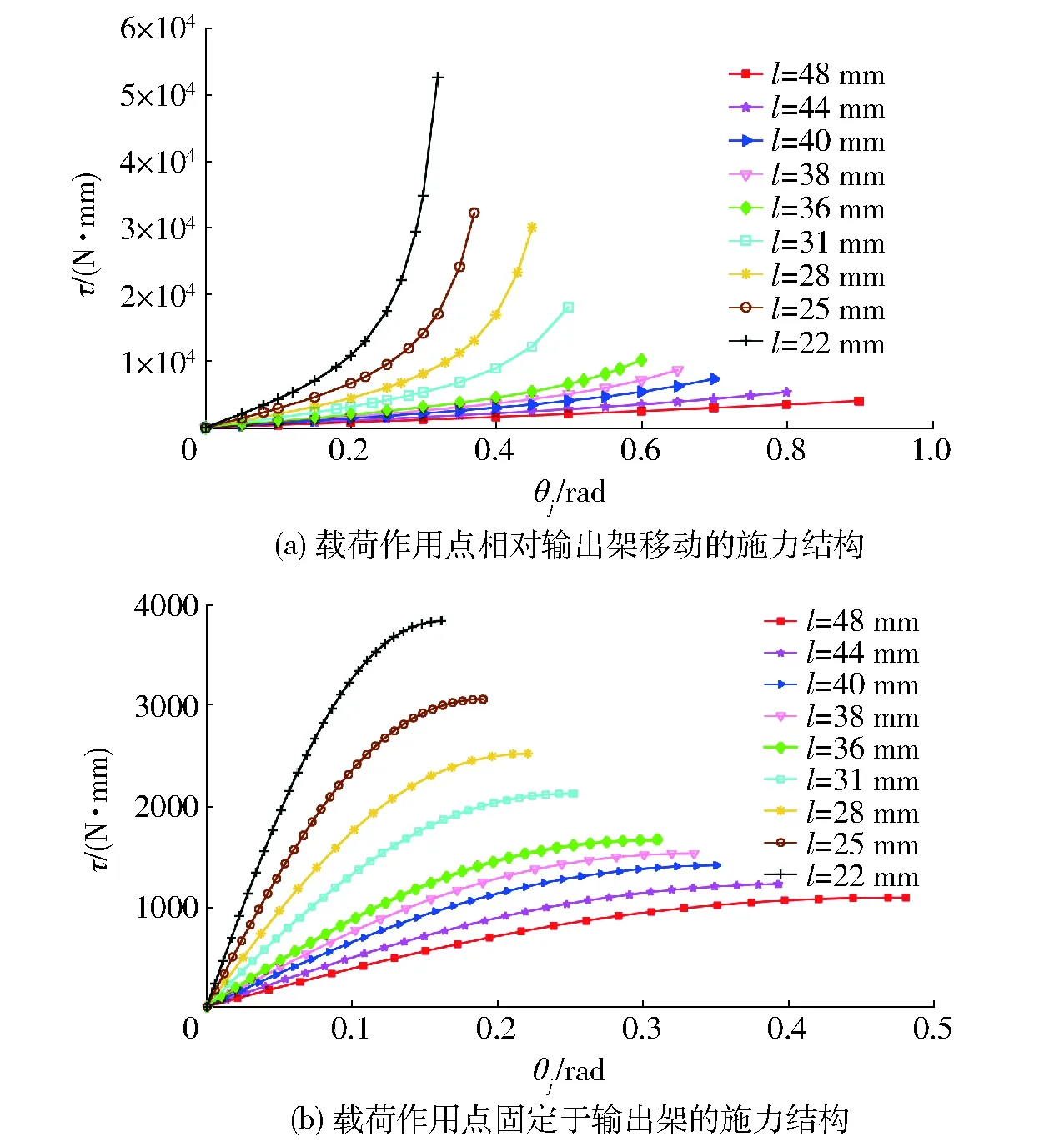
图7 外力矩τ与关节偏角θj的关系Fig.7 Relationships of external moment τ and deflection angles θj

图8 外关节刚度kj与关节偏角θj的关系Fig.8 Relationships of joint stiffness kj and deflection angles θj
本关节将弹簧片并联在一起,输出架偏转时,2个弹簧片同时起作用,因此,可以使用抗弯系数较小的弹簧片来实现较大的关节刚度;通过改变弹簧片上滑杆的固定位置,可以实现2种末端施力结构,从而得到2种不同刚度变化特性,应用更广泛。
4 变刚度关节样机的刚度性能试验
变刚度关节样机的具体设计参数见表1,其差动轮系中的太阳轮齿数Ns为18,齿圈齿数Nr为54,因此,太阳轮、齿圈及行星架的转速关系为
(10)

图9 变刚度关节样机的刚度试验装置Fig.9 Experimental setup of prototype1.57步进电动机 2.42步进电动机 3.IMU 4.拉力传感器
样机刚度性能的试验装置如图9所示,绳子拉动关节旋转,拉力传感器测量作用在关节上的力,输出架上的IMU(惯性测量单元)测量关节偏转角度。在变刚度关节上,对2种弹簧片末端施力结构的刚度特性进行试验。当弹簧片的有效长度l分别为28、38、48 mm时,关节所受外力矩τ随偏角θj变化如图10所示。由图10可以看出,试验结果与仿真结果出现一定的偏差。试验中,当关节偏角较大时,弹簧片产生大挠度变形,此时也会发生材料非线性变形,其中,蠕变、塑性变形等会引起非保守力问题,随着偏角的增大上述因素的影响也逐渐增加。根据试验数据的拟合曲线得到试验的关节刚度,如图11所示,试验数据的拟合刚度与仿真结果相近,证明了对于2种弹簧片末端结构刚度特性分析的正确性,并且该关节能够通过改变弹簧片末端结构来满足不同应用目的。

图10 关节力矩τ的试验结果与仿真结果对比Fig.10 Comparison of experimental and simulation results of external moment τ
对关节刚度调节性能进行试验,采用价格低廉的步进电机,曲柄上的IMU用来测量调节刚度时曲柄的旋转角度,并根据式(4)计算得到的弹簧片有效长度的变化,结果如图12所示,在2 s内,关节的刚度可以由最小调节到最大,调节速度快。
5 结论
(1)提出了一种仿生变刚度关节,利用差动轮系中行星轮的自转与公转分别实现关节刚度与位置的独立控制。该关节可以采用2种弹簧片末端施力结构分别实现不同的变刚度特性,1种末端施力结构使刚度随着偏角的增加而增大,而采用另1种结构的关节刚度随着偏角的增大而减小。
(2)变刚度关节样机的刚度性能试验结果与仿真结果一致,证明了弹簧片末端施力结构对关节偏转时的刚度变化的影响较大,并且该关节具有刚度变化范围大的特点。当关节应用在需要提供连续高刚度的情况时,采用载荷作用点相对输出架移动的弹簧片末端施力结构;当要求提高碰撞安全性时,关节刚度需在偏转过程中减小,此时变刚度关节可采用载荷作用点固定于输出架的末端施力结构。

图11 刚度kj的试验数据拟合结果与仿真结果对比Fig.11 Comparison of experimental fitting results with simulation results of joint stiffness kj
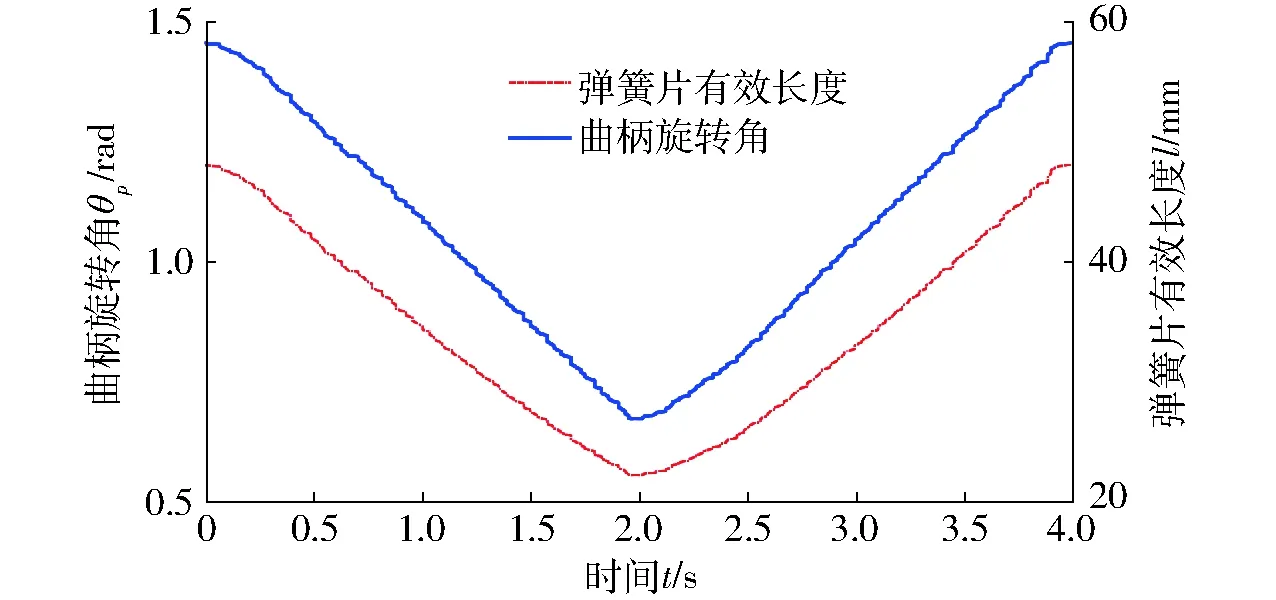
图12 曲柄的旋转角度及弹簧片有效长度的变化范围Fig.12 Rotation angle of crank and changing range of effective length
1 HAM V R, SUGAR T G, VANDERBORGHT B, et al. Compliant actuator designs: review of actuators with passive adjustable compliance/controllable stiffness for robotic applications[J]. IEEE Robotics Automation Magazine, 2009, 16(3): 81-94.
2 朱银龙, 张鑫焱, 王化明,等. 介电型电活物聚合物驱动转动关节控制技术研究[J/OL].农业机械学报,2015, 46(7): 333-338,332. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20150747&journal_id=jcsam.DOI:10.6041/j.issn.1000-1298.2015.07.047. ZHU Y L, ZHANG X Y, WANG H M, et al. Research on actuation control of dielectric elecroactive polymer rotary joint[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(7): 333-338,332.(in Chinese)
3 何天虎, 陈程, 崔磊磊.电活性聚合物薄膜万能肌肉作动器的力电非线性变形分析[J].工程力学,2011, 28(8): 232-239. HE T H, CHEN C, CUI L L. The mechanical-electro nonlinear deformation analysis of universal muscle actuators made of electro-active polymer membrane[J]. Engineering Mechanics, 2011, 28(8):232-239.(in Chinese)
4 谢胜龙, 刘海涛, 梅江平, 等. 基于高速开关阀的气动人工肌肉轨迹跟踪控制仿真[J/OL].农业机械学报,2017, 48(1): 368-374,385. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20170149&journal_id=jcsam. DOI: 10.6041/j.issn.1000-1298.2017.01.049. XIE S L, LIU H T, MEI J P, et al. Simulation of tracking control of pneumatic artificial muscle based on fast switching valves[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2017, 48(1): 368-374,385.(in Chinese)
5 项超群, 郝丽娜, 张颖,等. 软体手臂刚度特性分析[J/OL].农业机械学报,2017, 48(6): 407-412. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20170654&flag=1. DOI: 10.6041/j.issn.1000-1298.2017.06.054. XIANG C Q, HAO L N, ZHANG Y, et al. Analysis of stiffness characteristcs of soft arm[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2017, 48(6): 407-412.(in Chinese)
6 王颜, 房立金. 机械式仿骨骼肌变刚度机构原理及设计[J].机器人,2015, 37(4): 506-512. WANG Y, FANG L J. Principle and design of mechanically musculoskeletal variable-stiffness mechanism[J]. Robot, 2015, 37(4): 506-512.(in Chinese)
7 HAM V R, VANDERBORGHT B, DAMME M V, et al. MACCEPA, the mechanically adjustable compliance and controllable equilibrium position actuator: design and implementation in a biped robot[J]. Robotics and Autonomous Systems, 2007, 55(10): 761-768.
8 OSADA M, ITO N, NAKANISHI Y, et al. Realization of flexible motion by musculoskeletal humanoid “Kojiro” with add-on nonlinear spring units[C]∥ 2010 IEEE/RAS International Conference on Humanoid Robots, 2010:174-179.
9 FRIEDL W, CHALON M, REINECKE J, et al. FAS—a flexible antagonistic spring element for a high performance over actuated hand[C]∥2011 IEEE/RSJ International Conference on Intelligent Robots and Systems, 2011:1366-1372.
10 VANDERBORGHT B, TSAGARAKIS N G, HAM R V, et al. MACCEPA 2.0: compliant actuator used for energy efficient hopping robot Chobino 1D[J]. Autonomous Robot, 2011, 31(1): 55-65.
11 NAM K H, KIM B S, SONG J B. Compliant actuation of parallel-type variable stiffness actuator based on antagonistic actuation[J]. Journal of Mechanical Science and Technology, 2010, 24(11): 2315-2321.
12 GROOTHUIS S S, RUSTICELLI G, ZUCCHELLI A, et al. The variable stiffness actuator vsaUT-Ⅱ: mechanical design, modeling, and identification[J]. IEEE/ASME Transactions on Mechatronics, 2014, 19(2): 589-597.
13 KIM B S, SONG J B. Hybrid dual actuator unit: a design of a variable stiffness actuator based on an adjustable moment arm mechanism[C]∥ 2010 IEEE International Conference on Robotics and Automation, 2010:1655-1660.
14 JAFARI A, TSAGARAKIS N G, SARDELLITTI I, et al. A new actuator with adjustable stiffness based on a variable ratio lever mechanism[J]. IEEE/ASME Transactions on Mechatronics, 2014, 19(1): 55-63.
15 TAO Y, WANG T M, WANG Y Q. A new variable stiffness robot joint[J]. Industrial Robot, 2015, 42(4): 371-378.
16 CHOI J, HONG S, LEE W, et al. A robot joint with variable stiffness using leaf spring[J]. IEEE Transactions on Robotics, 2011, 27(2): 229-238.
17 WANG R J, HUANG H P. ADEA—active variable stiffness differential elastic actuator: design and application for safe robotics[C]∥ IEEE International Conference on Robotics and Biomimetics, 2011:2768-2773.
18 NASELLI G A, RIMASSA L, ZOPPI M, et al. A variable stiffness joint with superelastic material[J]. Meccanica, 2016:1-13.
19 HOWELL L L. 柔顺机构学[M]. 余跃庆,译. 北京:高等教育出版社,2007.
20 葛如海, 储志俊. 悬臂梁集中载荷大挠度弯曲变形的一种解[J]. 应用力学学报,1997,14(4):71-77. GE R H, CHU Z J. A way to calculate the deformation of great flexibility of slender long overhanging beam under concentrated load[J]. Chinese Journal of Applied Mechanics, 1997, 14(4): 71-77.(in Chinese)
21 KIMBALL C, TSAI L W. Modeling of flexural beams subjected to arbitrary end loads[J]. Journal of Mechanical Design, 2002, 124(2):223-235.
