自动导航插秧机路径跟踪系统稳定性模糊控制优化方法
2018-03-01唐小涛陶建峰李志腾李彦明刘成良
唐小涛 陶建峰 李志腾 李彦明 刘成良
(上海交通大学机械与动力工程学院, 上海 200240)
0 引言
自动导航技术对于开展精准农业研究和实践具有重要意义[1-2]。作为自动导航控制系统的核心,农机的路径跟踪系统对于提高作业质量和作业效率有决定性作用。目前关于路径跟踪的方法,国内外已有许多学者进行了大量研究,包括智能控制[3-5]、最优控制[6-7]、PID控制[8-11]和纯追踪模型[3,12-14]等方法。智能控制包括神经网络方法、模糊控制等,其优点是不要求为农机建立精确的运动学模型或动力学模型,但是神经网络在训练时需要有高质量的训练样本。最优控制对模型精度要求较高,为方便计算需要对农机非线性的运动学模型进行线性化处理。PID控制参数的整定一般比较困难,并且单变量PID控制只考虑了横向偏差而忽略了航向角偏差的影响[8-9,11],文献[10]虽然提出了用双变量PID的方法把横向偏差和航向角偏差同时作为反馈,但是并没有解决2个反馈变量之间的融合问题。纯追踪模型自从由卡耐基梅隆大学应用在无人驾驶汽车的路径跟踪控制上以来[15-16],由于其模型简单、参数易调的优点得到了广泛应用。作为纯追踪模型的唯一可调参数,前视距离会影响系统对目标路径的跟踪效果,前视距离过大或过小都难取得较好的跟踪效果。由于速度对基于纯追踪模型的路径跟踪控制系统稳定性的影响[17-18],速度太大会导致跟踪目标路径时系统发生振荡。为避免振荡以及跟踪上目标轨迹所需的行程太长,在不同的车身速度下运行的纯追踪模型也要求具备不同的前视距离。而传统前视距离固定的纯追踪模型,其数学公式中没有考虑速度参数,明显不能适应速度的变化。对于纯追踪模型前视距离的优化问题,文献[3,19]也采用了利用模糊控制来自适应调整前视距离的方法,但是把农机做恒速处理,仅以横向偏差和航向角偏差作为模糊控制器的输入,虽然对初始横向偏差有一定的鲁棒性和适应性,但是缺乏对速度变化的适应能力。实际上,插秧机在田间作业时,水田土壤环境和负载等都会影响车身速度。同时为了确保作业安全,车身速度必须根据车身姿态主动进行调整。文献[5,20]在调整前视距离时虽然考虑了速度的影响,但是提出的经验公式并不适合其他农机,需要通过大量实验才能确定公式参数。
本文提出用模糊控制优化前视距离,通过提高路径跟踪系统对速度的适应性改善其稳定性。该方法的模糊控制规则考虑速度因素,以速度和横向偏差作为模糊控制器的输入,在线自适应调整前视距离。为了证明该方法对不同速度的适应性,分别在高速1 m/s和低速0.3 m/s下进行实验。
1 运动学模型
1.1 车身运动学模型
以目标路径AB为Y轴,垂直于直线AB的方向为X轴,建立如图1所示的XOY直角坐标系,则车身的横向偏差d等于其横坐标x。直线AB的方向为从B点指向A点,且车身航向与直线AB方向的夹角绝对值不大于90°。在此坐标系下,将水田插秧机模型简化成二轮车模型,以后轮轴中心作为控制点,建立插秧机的运动学模型为
(1)
式中d——横向偏差,在直线AB右侧为正v——车身速度y——车身Y方向行进距离θ——航向角,逆时针方向为正l——前后轴距δ——前轮实际转角,左转方向为正

图1 插秧机坐标系Fig.1 Coordinate of tractor
1.2 自动转向环节建模
水田插秧机的方向盘采用步进电动机驱动,步进电动机转速与控制器输出成正比,所以插秧机的整个自动转向系统可以看作是一阶惯性环节,表达式为
(2)
式中δU——前轮目标转角,左转方向为正T——一阶惯性环节时间常数
转弯曲率和前轮转角δ之间的关系为
(3)
式中γ——实际转弯曲率,车身逆时针转动时为正
前轮转角为小角度时,式(3)可以线性化得
(4)
所以插秧机转向曲率的变化过程也可以看作是一阶惯性环节
(5)
式中γu——目标转弯曲率,车身逆时针转动时为正
因此跟踪直线时,纯追踪模型下的插秧机运动学模型为
(6)
2 纯追踪模型
纯追踪模型直线跟踪原理图如图2所示。其中O1为插秧机转向时的瞬时圆心,R为瞬时转弯半径,车身逆时针运动时为正,前视距离Ld相当于当前位置C(插秧机后轮轴中心)与预瞄位置D之间的弦长。

图2 纯追踪模型直线跟踪原理图Fig.2 Line tracking schematic diagram of pure pursuit model
在弦长一定的情况下,沿着前进方向可以在目标轨迹AB上找到唯一一点D作为预瞄位置。由已知两点坐标以及其中一点的切线方向可以确定一个圆可知,根据当前车身位置C的坐标、当前车身航向角以及预瞄位置D的坐标3个信息可以确定一个圆。当前车身位置与预瞄位置之间的这段圆弧即为插秧机接下来的理论运动路径,根据圆弧的曲率就可以求出插秧机接下来的理论前轮转角。一个周期过后,控制系统再重新根据车身位置和航向角,规划理论运动路径并计算出理论前轮转角。不断重复以上步骤,插秧机走过的实际路径会无限趋近目标路径。纯追踪模型数学公式的推导过程如下。
过预瞄位置D作车身航向的平行线交半径O1C于E点,线段CE的长度为L1,线段DE的长度为L2,φ为弦CD对应的圆心角,则
L1=-R(1-cosφ)
(7)
L2=-Rsinφ
(8)
由几何关系可知
(9)
(10)
(11)
由式(7)~(9)可得
(12)
将式(10)、(11)代入式(12)得
(13)
对应的曲率为
(14)
3 稳定性分析
(15)
其中
(16)
系统特征多项式为

(17)
简化得
(18)
由劳斯稳定性判据可知,系统在平衡位置处稳定的充要条件为
(19)
将式(14)、(16)代入式(19)得
Ld≥Tv
(20)
4 模糊控制器设计
4.1 输入输出变量模糊化
以横向偏差和车身速度为模糊控制器的输入,前视距离为其输出,首先对输入输出变量进行模糊化。
(1)横向偏差d。基本论域为:[-0.5, 0.5],量化等级为:{-1,-0.5,0,0.5,1}={NL, NS, Z, PS, PL},量化因子取2。
(2)车身速度v。基本论域为:[0,1.5],量化等级为:{0,0.5,1}={Z, S, L},量化因子取2/3。
(3)前视距离Ld。基本论域为:[0,6],量化等级为:{0,0.25,0.5,0.75,1}={Z, S, M, L, VL},量化因子取4。
为防止车身速度很小以及横向偏差偏大的时候出现前视距离小于横向偏差的情况,给模糊控制器的输出加上一个偏移量Ld0=0.5。
4.2 模糊规则设计原则
虽然取较小的前视距离可以使车身尽快趋近目标位置,但是另一方面会导致严重的超调现象,甚至有可能导致系统不稳定;而前视距离越大,虽然车身实际行走轨迹会比较平稳,但是逼近目标轨迹所需时间太长。即前视距离过大或者过小都不会取得较好的跟踪效果。在设计模糊规则时,应考虑以下原则:①横向偏差越小,前视距离越大;横向偏差越大,前视距离越小。②在满足稳定性条件下,速度越大,前视距离越大;速度越小,前视距离越小。
模糊规则如表1所示,模糊控制曲面如图3所示。
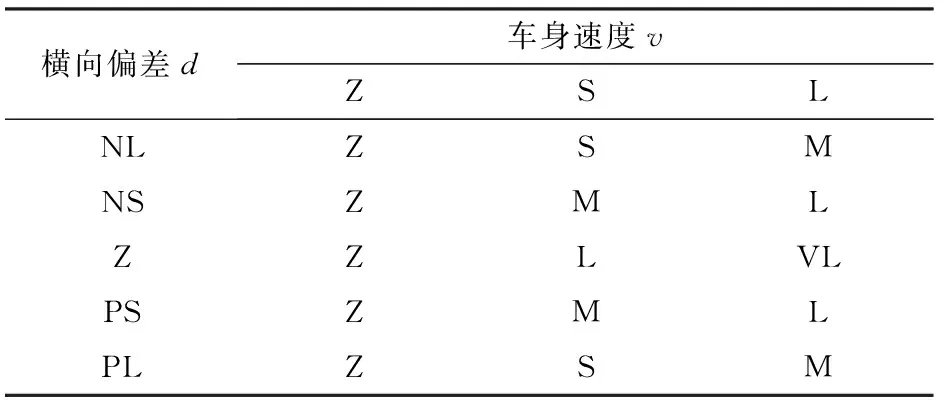
表1 模糊控制规则Tab.1 Fuzzy control regulation
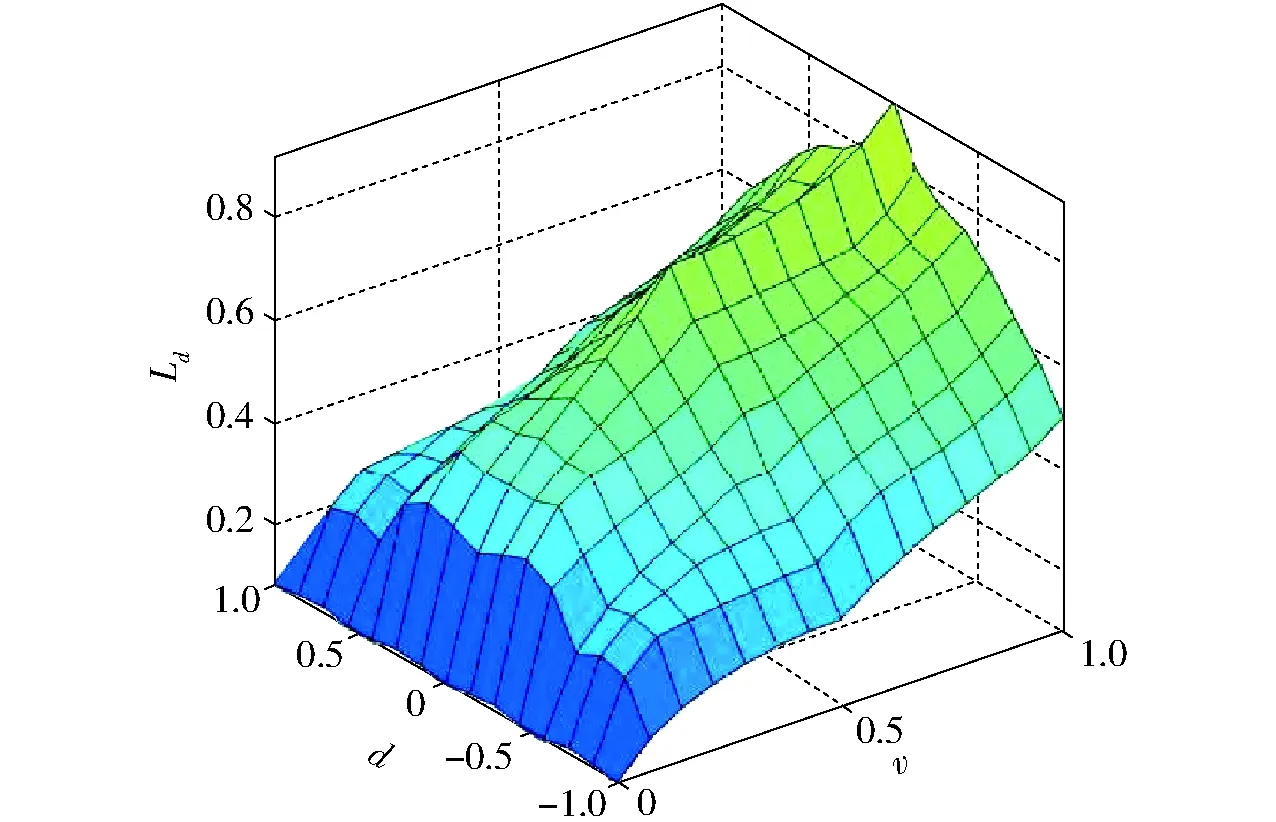
图3 模糊控制曲面Fig.3 Surface of fuzzy model
5 实验与分析
5.1 实验平台
洋马VP6E型水田插秧机经过自动化改造后,包括插秧机本体、北斗/GNSS高精度差分定位系统、导航控制器、自动转向系统、车轮转角测量传感器等,插秧机本体以及实验环境如图4所示。

图4 实验平台Fig.4 Experimental platform
北斗高精度差分定位系统由上海联适导航公司提供,由基站和移动站组成。其中基站包括R30接收机、一个定位天线和电台通信模块,安装在空旷地面上的固定位置,用于接收北斗/GNSS卫星数据。移动站包括R60接收机、2个定位天线和电台通信模块,安装在插秧机上面,其中2个定位天线分为主天线和副天线。通过电台接收来自基站的参考坐标信号,再通过差分算法计算得出移动站主天线的实时坐标位置。使用双天线是为了改善单天线在低速状态下的航向角精度。该定位系统的定位精度可达2.5 cm,航向角精度可达0.1°,数据传输频率为10 Hz。
转向系统采用步进电动机驱动插秧机原有的方向盘轴转动,步进电动机的机身与方向盘外的套筒固定,电动机转轴通过传动比为1∶2的同步轮减速系统与方向盘轴相连。步进电动机采用日本山社电机株式会社的TM2301PGA45A-5系列,保持扭矩为4 N·m。
车轮转角测量传感器采用北京世纪铭创公司提供的MCGJ485B系列绝对值角度编码器,满量程测量误差为±0.2°。
5.2 路径跟踪实验
分别在高速和低速两种情况下,对比插秧机利用固定前视距离的纯追踪模型和利用本文提出的方法跟踪直线的实验效果。考虑插秧机在田间作业时的速度范围,低速指车身速度为0.3 m/s,高速指车身速度为1.0 m/s。对于传统的固定前视距离的纯追踪模型而言,不同的车身速度对应着一个不同的最优前视距离。设定车身初始横向偏差为1 m,本文通过多次实验分别确定了车速为0.3 m/s时的最优前视距离为1.2 m,车速为1 m/s时的最优前视距离为3 m。实验对比结果如表2所示。
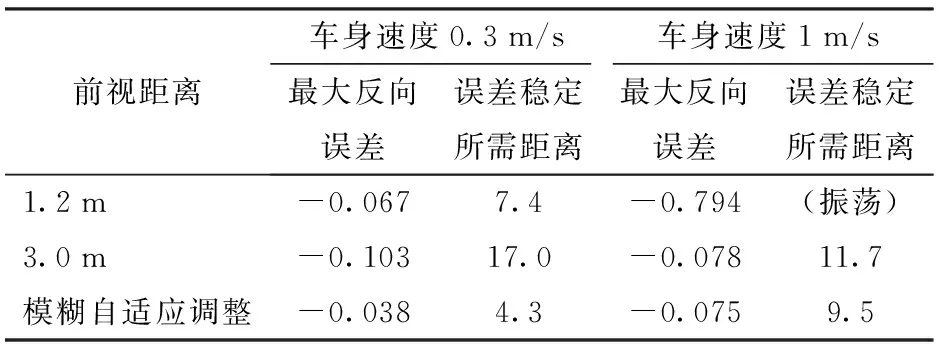
表2 实验结果Tab.2 Result of experiment m
在车速为0.3 m/s时,分别以前视距离为1.2、3.0 m和模糊调整进行直线跟踪实验,横向偏差的变化如图5所示。前视距离固定为1.2 m的纯追踪模型系统在前进7.4 m之后跟踪误差趋于稳定,而前视距离固定为3.0 m的控制系统在前进17 m后才趋于稳定,前者比后者能更快地向目标轨迹收敛。前视距离自适应调整的纯追踪模型方法和前视距离固定为1.2 m的方法相比,在跟踪前期都能在前进3 m左右接近目标路径,具有很快的收敛速度;随着横向偏差越来越小,模糊控制器输出的前视距离会变大,最大反向误差只有-0.038 m,继续前进至4.3 m跟踪误差趋于稳定,而固定前视距离为1.2 m的控制系统的最大反向误差达到-0.067 m,继续前进至7.4 m误差才趋于稳定。

图5 车速为0.3 m/s时的横向偏差变化曲线Fig.5 Lateral deviation curves at 0.3 m/s
在车速为1.0 m/s时,同样以上述3种前视距离进行实验,横向偏差的变化如图6所示。实验结果表明,前视距离固定为1.2 m的纯追踪模型在跟踪目标路径时发生了振荡现象,说明此时的纯追踪模型已经不满足稳定性条件。采用前视距离自适应调整的纯追踪模型控制策略,插秧机前进9.5 m后跟踪误差趋于稳定;而在前视距离固定为3.0 m的纯追踪模型方法下,插秧机跟踪上目标轨迹至少需要10 m。

图6 车速为1 m/s时的横向偏差变化曲线Fig.6 Lateral deviation curves at 1 m/s
根据以上对比实验可知,固定的前视距离并不能适应整个速度范围内的路径跟踪。前视距离太小,在速度快时容易导致系统不稳定;前视距离太大,在速度慢时跟踪目标轨迹不及时。本文提出的根据模糊控制器自适应调整纯追踪模型前视距离的方法,能够根据速度变化和横向偏差的变化实时调整纯追踪模型的前视距离,对速度具有更好的适应性,同时也能改善纯追踪模型的跟踪效果,使插秧机更快跟踪上目标轨迹。
从图5和图6可以发现,直线跟踪进入稳态阶段后,插秧机与目标轨迹之间始终存在一定的稳态偏差,不管是传统的固定前视距离的纯追踪模型,还是本文提出的前视距离变动的纯追踪模型都无法消除这一偏差,其产生原因是因为导航系统的航向角坐标系与车身坐标系之间的偏差以及插秧机前轮转角测量传感器的零位偏差。
6 结论
(1)以速度和横向偏差作为输入,建立模糊控制器自适应调整纯追踪模型的前视距离。首先建立了自动转向系统为一阶惯性环节的插秧机运动学模型,基于此模型分析了纯追踪模型的稳定性条件,分析结果表明,速度影响纯追踪模型的稳定性。在满足稳定性条件的基础上建立模糊控制规则。
(2)为了验证方法的有效性,分别在插秧机以高速1.0 m/s和低速0.3 m/s运动的情况下进行了实验,实验结果表明,本文提出的方法对不同的车身速度都具有适应性,在速度较快时能避免插秧机跟踪目标轨迹时发生振荡,有效改善了路径跟踪控制系统的稳定性。
1 胡静涛,高雷,白晓平,等. 农业机械自动导航技术研究进展[J]. 农业工程学报,2015,31(10):1-10. HU Jingtao, GAO Lei, BAI Xiaoping, et al. Review of research on automatic guidance of agricultural vehicles[J]. Transactions of the CSAE, 2015, 31(10): 1-10. (in Chinese)
2 BU Xuhui, HOU Zhongsheng, CHI Ronghu. Model free adaptive iterative learning control for farm vehicle path tracking[J]. IFAC Proceedings Volumes,2013,46(20):153-158.
3 李逃昌,胡静涛,高雷,等. 基于模糊自适应纯追踪模型的农业机械路径跟踪方法[J/OL].农业机械学报,2013,44(1):205-210.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20130139&journal_id=jcsam. DOI:10.6041/j.issn.1000-1298.2013.01.039. LI Taochang, HU Jingtao, GAO Lei, et al. Agricultural machine path tracking method based on fuzzy adaptive pure pursuit model[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2013, 44(1):205-210. (in Chinese)
4 周建军, 张漫, 汪懋华,等. 基于模糊控制的农用车辆路线跟踪[J]. 农业机械学报, 2009, 40(4):151-156. ZHOU Jianjun, ZHANG Man, WANG Maohua, et al. Path tracking for agricultural vehicle based on fuzzy control[J]. Transactions of the Chinese Society for Agricultural Machinery, 2009, 40(4):151-156. (in Chinese)
5 张闻宇,丁幼春,王雪玲,等. 基于SVR逆向模型的拖拉机导航纯追踪控制方法[J/OL]. 农业机械学报,2016,47(1):29-36.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20160105&journal_id=jcsam.DOI:10.6041/j.issn.1000-1298.2016.01.005. ZHANG Wenyu, DING Youchun, WANG Xueling, et al. Pure pursuit control method based on SVR inverse-model for tractor navigation[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(1):29-36. (in Chinese)
6 周俊,姬长英,刘成良. 农用轮式移动机器人视觉导航系统[J]. 农业机械学报,2005,36(3):90-94. ZHOU Jun, JI Changying, LIU Chengliang. Visual navigation system of agricultural wheeled-mobile robot[J]. Transactions of the Chinese Society for Agricultural Machinery, 2005, 36(3):90-94. (in Chinese)
7 周俊. 农用轮式移动机器人视觉导航系统的研究[D].南京:南京农业大学,2003. ZHOU Jun. Research on visual navigation for agriculture wheeled mobilerobot[D].Nanjing:Nanjing Agricultural University, 2003.(in Chinese)
8 DONG F, HEINEMANN W, KASPER R. Development of a row guidance system for an autonomous robot for white asparagus harvesting[J]. Computers and Electronics in Agriculture, 2011, 79(2):216-225.
9 罗锡文,张智刚,赵祚喜,等. 东方红X-804拖拉机的DGPS自动导航控制系统[J]. 农业工程学报,2009,25(11):139-145. LUO Xiwen, ZHANG Zhigang, ZHAO Zuoxi, et al. Design of DGPS navigation control system for Dongfanghong X-804 tractor[J]. Transactions of the CSAE, 2009, 25(11): 139-145.(in Chinese)
10 姜勇. 基于双变量PID控制算法的地下智能铲运机自主导航技术研究[J]. 机械制造, 2016, 54(5):19-22,31.
11 熊中刚,叶振环,贺娟,等. 基于免疫模糊PID的小型农业机械路径智能跟踪控制[J]. 机器人, 2015(2):212-223. XIONG Zhonggang, YE Zhenhuan, HE Juan, et al. Small agricultural machinery path intelligent tracking control based on fuzzy immune PID[J].Robot, 2015(2):212-223.(in Chinese)
12 SAMUEL M, HUSSEIN M, BINTI M. A review of some pure-pursuit based path tracking techniques for control of autonomous vehicle[J]. International Journal of Computer Applications, 2016, 135(1):35-38.
13 SHAN Y, YANG W, CHEN C, et al. CF-pursuit: a pursuit method with a clothoid fitting and a fuzzy controller for autonomous vehicles[J]. International Journal of Advanced Robotic Systems, 2015, 12(9): 134.
14 黄沛琛,王紫虹. 基于纯追踪曲线跟踪模型的车辆自动导航[J]. 自动化应用,2011(4):23-27. HUANG Peichen, WANG Zihong. Pure pursuit curve tracking model research for vehicle automatic guidance[J]. Automation Application, 2011(4):23-27. (in Chinese)
15 WALLACE R, STENTZ A, THORPE C E, et al. First results in robot road-following[C]∥IJCAI, 1985: 1089-1095.
16 AMIDI O, THORPE C E. Integrated mobile robot control[C]∥Fibers’91, International Society for Optics and Photonics, 1991: 504-523.
17 MURPHY K N. Analysis of robotic vehicle steering and controller delay[C]∥Fifth International Symposium on Robotics and Manufacturing (ISRAM), 1994: 631-636.
18 OLLERO A, HEREDIA G. Stability analysis of mobile robot path tracking[C]∥ International Conference on Intelligent Robots and Systems, IEEE Computer Society, 1995:3461.
19 汪小旵,鲁伟,陈满,等. 基于改进纯追踪模型的温室采摘运输自动跟随系统[J/OL]. 农业机械学报,2016,47(12):8-13.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20161202&journal_id=jcsam. DOI:10.6041/j.issn.1000-1298.2016.12.002. WANG Xiaochan, LU Wei, CHEN Man, et al. Automatic following system for greenhouse harvesting transportation based on adaptive pure pursuit model[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2016,47(12):8-13. (in Chinese)
20 ZHANG Q, QIU H. A dynamic path search algorithm for tractor automatic navigation[J]. Transactions of the ASAE, 2004, 47(2): 639-646.
