水下舷外发射水密隔膜运动特性数值仿真研究
2018-03-01吴明晨
吴明晨,苏 杭,赵 铮
(1.中船重工713研究所六室, 河南 郑州 450052; 2.南京理工大学 能源与动力工程学院, 江苏 南京 210094)
水下发射装置的研究及其设计,对于提高鱼雷、潜射导弹等武器的出水品质具有十分重要的意义。对于有关弹丸的水下发射过程的研究,李亚男[1]通过建立热力学模型,对小型运载器的弹丸发射过程进行了仿真;李志华[2]通过建立鱼雷的运动方程,作出了鱼雷的弹道曲线,并确定鱼雷不会产生很大的袋深现象;程广涛[3]对水下发射系统进行了数学建模,确定了发射过程中发射系统参数和武器运动参数。
水下发射的主要困难在于整流罩和耐压壳之间的空间狭小,对发射装置水密隔膜的结构设计要求较高,水密隔膜在张开或散布过程中不能与邻筒发生干涉。目前水下发射装置水密隔膜多采用不系留方式,即水密隔膜破裂后与发射筒分离。该方式虽然结构简单,但无法控制水密隔膜破片的散布范围,在多筒同时发射或小间隔发射时隔膜破片容易碰撞邻筒弹体。本文设计了一种水下弦外发射水密隔膜系留结构,通过转轴连接水密隔膜和发射筒,使破裂后的水密隔膜系留在发射筒上,控制隔膜翻转角度避免与邻筒发生干涉。
由于发射筒为多单元联装结构,单元间距离较小,水密隔膜在张开过程中所占据的空间逐渐增大,因此,需要计算在不同发射条件下,水密隔膜的最大张开角度。本文主要研究水密隔膜在发射过程中的运动特点,不考虑发射装置的动力部分及相关影响。
1 计算模型的建立
本文所研究的水下舷外发射装置由发射筒、水密隔膜、滑块滑轨、动力系统和弹体组成。滑块位于弹体尾部,动力系统推动滑块使弹体沿滑轨在发射筒内加速运动,弹头冲破水密隔膜后弹体发射出筒。计算模型由水域、鱼雷、鱼雷发射筒、水密隔膜和相对应安装在发射筒上的铰链转轴所组成。
计算域后部为鱼雷,鱼雷前部为球冠,后部为空心的圆柱体,材料为钢,模型质量与实际鱼雷质量相同;鱼雷前部为四瓣水密隔膜,材料为有机玻璃,扁球壳状;水域为给定水深的海水;鱼雷发射筒和水密隔膜将鱼雷与水域分隔开;自行设计铰链转轴机构,在Solid Edge软件环境下进行建模,其结构模型图如图1,计算域模型如图2。

图1 铰链转轴模型三视图及三维图

图2 计算域示意图
2 有限元分析模型的建立
流固耦合计算需要同时考虑流场冲击和弹丸运动的相互作用,包括流场计算、固体力学计算、耦合计算等。在保证计算精度的条件下,需要对计算模型简化,以减少计算时间,提高计算速度。
采用cm-g-μs单位制对计算域进行建模,本系统的有限元模型由水域、鱼雷发射筒、水密隔膜、弹丸和铰链转轴组成。经过ICEM软件进行网格划分后,得到铰链转轴的有限元网格如图3,整个计算域的有限元网格如图4所示。
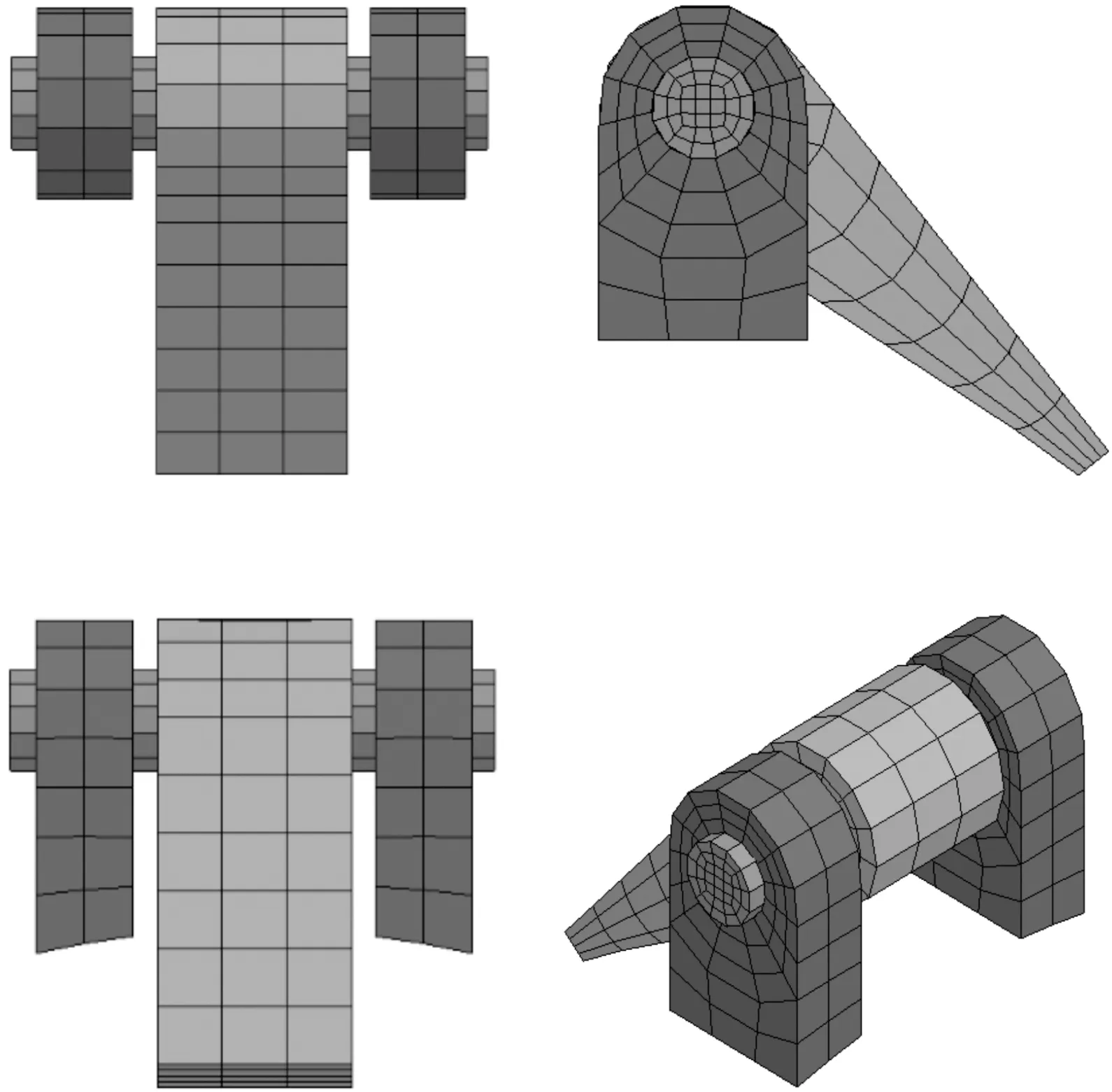
图3 铰链转轴网格三视图及三维图

图4 计算域网格
其中水介质采用欧拉网格建模, GRUNEISEN状态方程[4];弹丸、发射筒和铰链转轴均为钢材料,采用拉格朗日网格建模,MAT_JOHNSON_COOK材料模型[5];水密隔膜采用有机玻璃材料,采用MAT_ELASTIC弹性材料模型[6]。计算中采用的水介质和发射装置的材料及状态方程参数如表1、表2所示,未给出的参数取 LS-DYNA软件和工程实践中的默认值。

表1 不同模型的材料参数

表2 水介质的材料参数
约束设置与接触设置为:在水-结构边界,通过Euler/Lagrange罚函数耦合算法建立约束方程,将发射装置结构与水域流体进行耦合计算[7];采用转轴实现水密隔膜与发射筒的连接,铰链转轴的固连面采用面面固连接触,接触面采用自动面面接触。为节约求解时间和计算量,将发射装置放在流场的中心对称位置。对于外流场设置,通过定义不同的水深-密度曲线间接模拟不同水深时的环境压力[8];在水域边界面施加透射边界约束,模拟无限水域。
对于初始条件设置,设定弹丸以给定速度曲线运动;设定发射装置以恒定速度运动,即以一定的艇速运动。
对于控制设置,为了避免沙漏现象的产生,采用沙漏控制语句*CONTROL_HOURGLASS,在语句中的默认沙漏系数为0.03;*CONTROL_TIMESTEP控制语句的时间步长比例因子为0.9,有效的防止了负体积的产生;基本计算时间为0.6 s,每隔0.6 ms输出一个d3plot结果文件。
3 水密隔膜破裂过程分析
通过基于 LS-DYNA程序的多物质ALE 算法[9],对鱼雷发射过程进行了三维有限元模拟,并采用 LS-PREPOST 软件对 LS-DYNA 求解后得到的d3plot文件进行后处理[10]。在仿真过程中,为了减少计算量,外流场只选取了离弹丸较近的部分。
图5为在发射过程中,发射装置在不同时刻下(t=0 s,0.10 s,0.15 s,0.20 s)的状态变化图。由图5可以看出,随着时间的进行,水密隔膜绕着铰链转轴转动,从而水密隔膜由封闭状态缓慢张开,使弹丸有空间出筒。在发射过程中水密隔膜与弹丸没有直接接触。
4 不同发射条件下的水密隔膜转角变化
4.1 不同弹速条件下的影响
计算了不同弹速条件、水深150 m、无艇速条件下,水密隔膜的转动角度随时间的曲线,如图6。
由图6可以看出,水密隔膜转角先在t=0.2 s左右快速增大,后保持一定角度不变,当弹丸出筒后,由于弹丸尾部产生的低压区造成较大的压差阻力[11],因此在发射装置外部有海水补入,导致发射装置产生振动[12],水密隔膜转角达到最大值,并且在状态稳定以后转角保持不变。在不同的弹速条件下,水密隔膜的转角曲线趋势相同,且最大转角基本保持不变,大致为48°。
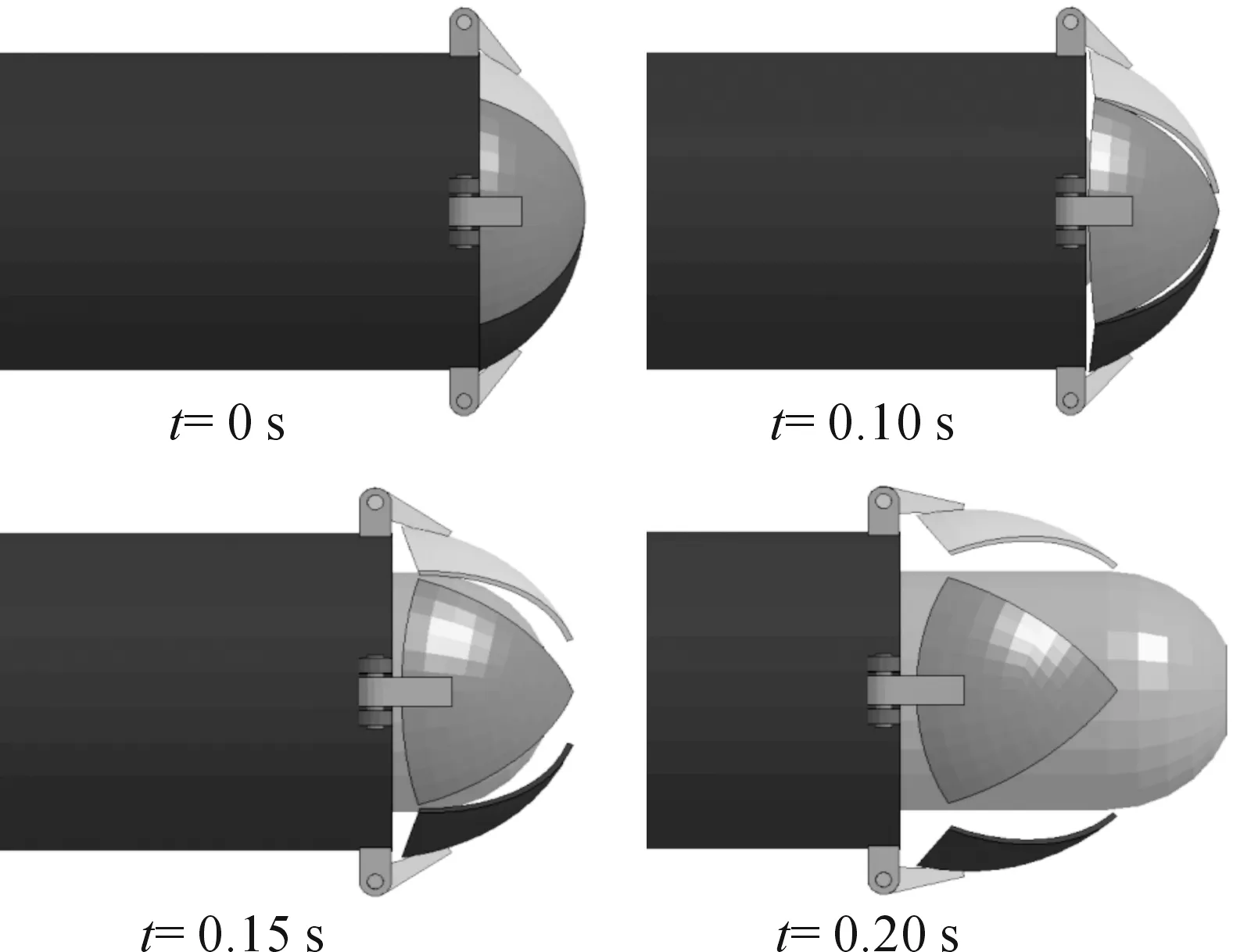
图5 发射装置及弹丸在不同时刻下的状态图

图6 弹速不同时的水密隔膜转角-时间曲线
4.2 不同水深条件下的影响
计算了不同水深条件、弹速12 m/s、无艇速条件下,水密隔膜转角随时间的曲线如图7。
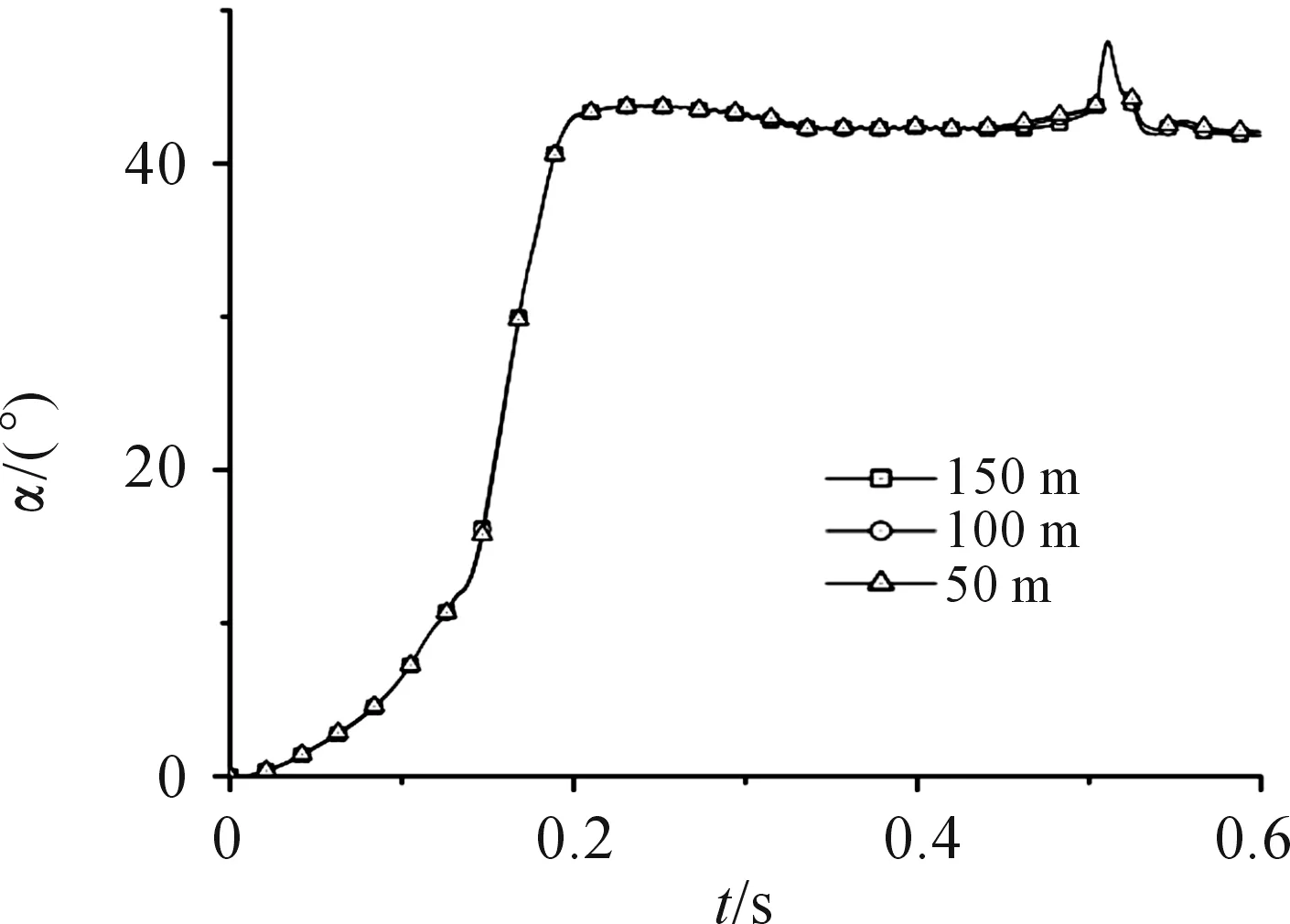
图7 不同水深条件下的水密隔膜转角曲线
由图7可以看出,不同水深条件下,水密隔膜转角曲线的趋势及峰值均相同,因此可以确定,不同水深条件对水密隔膜转角基本没有影响。
4.3 不同艇速条件下的影响
图8是在水深150 m、弹速12 m/s、不同艇速条件下的水密隔膜转角随时间的曲线图。

图8 艇速不同时的水密隔膜转角-时间曲线
将其与图7所示的无艇速条件下水密隔膜转角曲线相对比后可以看出:
在t=0-0.15 s左右的运动起始阶段,由于发射装置有艇速,弹丸实际速度比无艇速时大,因此在相同时间下,弹丸所推动的水的体积也相对增大,水密隔膜转角速度相比无艇速时明显增加;在t=0.15-0.45 s,为弹身出筒阶段,由于弹丸的实际速度为艇速加上推力所造成的速度,弹丸给水密隔膜的力也会相对增大,因此其在48°时,水密隔膜仍会继续转动。当其转动到61°左右,水密隔膜在轴向保持相对平衡状态,转角在61°左右基本不变;在t=0.45~0.6 s,弹丸已出筒,由于发射筒内需要海水的补入,因此水密隔膜转角会有一定程度的振荡,振荡过后基本保持稳定。整个发射过程中,水密隔膜转角的最大值为61°。
5 结论
1) 在给定不同弹速条件下,水密隔膜转角先迅速增加,后基本不变,随后由与弹丸出筒时产生的振荡达到峰值并有所回落,水密隔膜在发射过程中的最大转角为48°;
2) 在给定不同水深条件下,水密隔膜转角曲线基本不变,最大转角为48°;
3) 在给定艇速条件下,水密隔膜转角速度相比无艇速时有所增大,在转动61°左右时,水密隔膜在轴向达到相对平衡状态,并且在达到最大转角之后,转角曲线基本保持稳定,整个发射过程中水密隔膜的最大转角为61°。
由于在建模的过程中考虑到了水密隔膜的安装方式,和海水水压的作用,可以为水密隔膜结构模型设计提供一定指导,也可以为鱼雷发射装置设计提供参考。下一步设计应考虑水密隔膜实际结构对于发射装置的影响。
[1] 李亚男,叶慧娟,张西勇,等.水压平衡式鱼雷发射装置发射小型运载器内弹道仿真[J].兵器装备工程学报,2016,37(2):41-44.
[2] 李志华,阎勇,吴吉伟.鱼雷发射装置安全性仿真分析[J].四川兵工学报,2011,32(4):7-8.
[3] 程广涛,孔岩峰,张振山.液压平衡式水下武器发射系统仿真分析[J].兵工学报,2009,30(7):915-919.
[4] KUBOTA S,SABURI T,OGATA Y,et al.Numerical Modeling of Shock Initiation in PETN by Unified EOS[J].Science & Technology of Energetic Materials,2010,71(3):92-97.
[5] GREGORY.Failure Modeling of Titanium 6Al-4V and Aluminum 2024-T3 With the Johnson-Cook Material Model,September 2003.
[6] GURTIN M E,MURDOCH A I.A Continuum Theory of Elastic Material Surfaces[J].Archive for Rational Mechanics and Analysis,1975,57(4):291-323.
[7] 朱洪来,白象忠.流固耦合问题的描述方法及分类简化准则[J].工程力学,2007,24(10):92-99.
[8] AIAA.Dynamics Impact Tolerance of Shuttle Rcc Leading Edge Panels Using Ls-Dyna[C].Aiaa/Asme/Sae/Asee Joint Propulsion Conference and Exhibit.2005.
[9] ZHANG Z,SANG J,ZHANG Y.Inflation Analyses of a Circular Elastomeric Membrane With Hydrostatic Pressure[J].Theoretical and Applied Mechanics Letters,2012,2(6):15-18.
[10] 凡金金.沙粒碰撞平板模型的数值仿真研究[D].南京:南京航空航天大学,2016.
[11] 刘传龙,张宇文,王亚东,等.提拉活塞式导弹水下发射过程数值模拟[J].上海交通大学学报,2015(5):651-656.
[12] 傅德彬,于殿君,张志勇.潜射导弹离筒后海水倒灌效应数值分析[J].固体火箭技术,2012,35(2):157-160.
