基于模糊逻辑的轮速信号可信度监控∗

靳立强，陈鹏飞，黄建凌，刘蒙蒙

（1.吉林大学，汽车仿真与控制国家重点实验室，长春 130022； 2.浙江亚太机电股份有限公司，杭州 311203）

前言

轮速信号传感器是汽车上众多传感器中最重要的传感器之一[1]，是电子稳定控制系统(ESC)的基本输入信号之一，对一些关键参数，例如车轮滑移率、参考车速等计算至关重要[2]。而汽车本身又是一个复杂系统，行驶于各种复杂的工况时，作为弱电系统的轮速信号，难免会受到各种干扰的影响[3]。如果异常轮速信号输入到ESC系统内，可能会影响到控制效果，甚至产生反作用，进而影响到驾驶安全。因此，需要增强对轮速的故障监控能力[4]。

轮速的故障模式较多，可分为硬件电路的故障和信号数值异常，硬件故障的监测比较简单，通常集成在ECU的诊断电路中，而对数值异常的监控算法则比较复杂[5]。基于动力学模型和模糊逻辑的故障诊断技术在汽车电控系统中有不少的应用[6－8]。本文中基于这一思路，首先分析了异常信号产生的原因和特征，并对轮速信号计算过程中的脉冲、角速度、角加速度和角加速度变化的数值特征进行了分析，提出了一种参考线速度的简单计算方法，并基于模糊逻辑提出了一种轮速异常信号的监控方法。通过模糊逻辑来描述轮速信号的动力学特征，从而得到当前轮速信号的可信程度。

1 异常信号产生原因

轮速传感器的故障会导致轮速信号异常，但在某些情况下，轮速传感器本身并没有损坏，不过是由于其他干扰如广播电台和车辆振动等造成对轮速信号干扰，导致瞬时的轮速信号失真，此时轮速信号不可信。这种异常无法通过硬件电路进行监测，需要通过软件算法进行监控。尤其是在转速较低时，轮速信号更容易受到干扰。

轮速信号异常或者数值不可信时，可能出现以下状态特征:

(1)轮速信号频率过高；

(2)车轮加速度过大；

(3)车轮加速度变化率过大；

(4)低速状态下，轮速脉冲信号的边缘数量和间隔时间数值不可信时，轮速信号不可信；

(5)轮速原始值和滤波值的差值较大，轮速信号不可信。

本文中提出的可信度监控是通过对轮速信号的动力学状态进行观察分析，如加速度、轮速与车速的偏差等等。由于相关的动力学状态都是变化的，并且有些是由于偶然的干扰信号导致，有时偶然出现的几个干扰信号也无须把轮速信号置为异常状态。这就对监控算法的鲁棒性和自适应性提出了一定的要求。

本文中综合运用两种方法来监控轮速信号的可信度:一种是基于门限值的方法，不同的车速状态下，设定相关变量(边缘值、间隔时间、脉冲数、加速度和加速度变化率等)的门限值，当相应变量超过该门限值即可认为是轮速信号异常；另外一种方法是基于模糊逻辑，建立相关变量的可信度规则，判断轮速信号可信与否，这样可以改变监控的敏感度，增加监控逻辑的鲁棒性和自适应能力。基于门限值判断相关变量数值的错误与否，只能是刚性地设置一些门限值，这样会使监控程序对错误触发异常的敏感，可能会有一些错误的判断，而引入模糊逻辑，恰恰可以弥补这些不足。

新疆是温带大陆性气候，昼夜温差大，属典型的大陆性干燥气候。尤其是处于塔克拉玛干边缘的南疆部分地区，气候异常干燥，年降雨量较小，缺水严重，而当地土壤沙化现象严重，土壤保水能力差，缺水与土壤保水能力差的现状无疑增加当地棉花种植成本，成为制约当地经济快速发展的一个瓶颈。

2 相关变量分析

图1为轮速传感器信号采集的基本原理。单片机的捕获与比较单元记录输入的边缘数量，测量下降沿和上升沿的时间标记，以5ms为采样的时间周期，计算这些时间标记的间隔时间。之后基于输入的边缘数量和间隔时间，可继续计算得到角速度、角加速度和角加速度变化率等，下面对各个变量的特征和最大门限值进行分析。

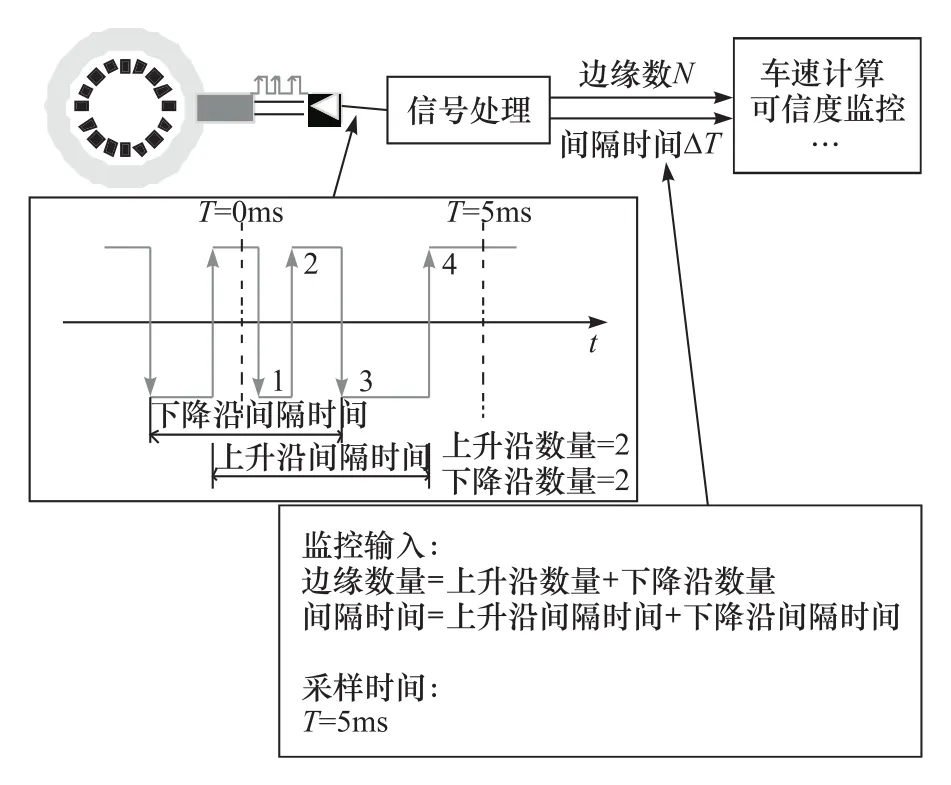
图1 时间间隔和边缘数量

(1)边缘数量的最大值 边缘数量的最大值按照最高车速换算，例如最高车速为240km/h时，对应最大边缘数量8个/5ms。

(2)时间间隔的最大、最小值 时间间隔的最大值和最小值与采集到的边缘数量有关系，单独统计间隔时间没有意义。根据采集到的边缘值设定间隔时间的对应数组，数组分别如下:边缘值输入:[0 1 2 3]，3个以上则按照3计算；最小错误间隔时间:[5 3.75 5.8 7.0]ms；最大错误间隔时间:[0xFFFFFFFF 0xFFFFFFFF 31 20]ms。其中，0xFFFFFFFF由变量的数值类型而来，有4个字节的占位。

(3)车轮角速度的最大值 按照单位时间内可能得到的最大角速度来设置，例如210rad/s。

(4)车轮角加速度的最大值 角加速度允许的最大值计算，只有在采集到边缘值或者速度不为0的情况下才有效，在没有轮速的情况下计算的最大值没有意义。在定义最大角加速度时，不仅要考虑到实际的行驶极限，还应该考虑到实际信号中掺杂的未能滤掉的噪声，因此不能将门限设置的过低。例如角加速度绝对值的最大值门限:1 885rad/s2。

(5)车轮角加速度变化率的最大值 与角加速度的门限值设定类似，角加速度变化率绝对值的最大值门限:30 000rad/s3。

(6)轮速原始值和滤波值之差的最大值 轮速原始值和滤波值之差的绝对值的最大值门限，要以车辆实际的信号作为基础分析，不同的车型可能需要不同的门限值，例如4.4rad/s。

3 参考线速度计算

根据轮速脉冲信号和齿圈齿数等参数可以计算得到各车轮旋转角速度ωi，则各个车轮线速度vxi＝2πrωi；当前各车轮线速度的最大值、最小值、平均值分别为 vmax，vmin和 vx，其中线速度平均值的计算是基于异常轮速信号以外的有效轮速信号；由于剔除了无效轮速信号的影响，所以计算出的参考线速度会更加准确。

当前时刻k的参考线速度简单计算为

其中:v(k)base＝vx＋βΔ vx

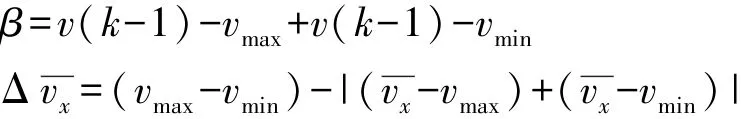
式中α为设定的系数常数。

4 基于模糊逻辑的轮速信号可信度监控

基于第2节中关于轮速异常状态特征的描述，建立故障监控的模糊规则。设输入向量:x＝{｜ω··i｜，｜ω·i｜，ωi，｜Δωi｜，｜ωi－v/2πr｜}，分别代表了各个车轮角加速度变化率的绝对值(x1)、角加速度的绝对值(x2)、角速度(x3)、角速度滤波值与原始值之差的绝对值(x4)和角速度与参考角速度差的绝对值(x5)。需要说明的是，参考角速度由参考线速度通过换算得到。

由于是对轮速信号的异常与否进行监控，因此没有必要把所有信号的各种状态隶属度都考虑在内，为了简化计算，只须考虑可能出现轮速信号不可信的典型工况即可。由于噪声而使轮速信号不可信时，最直观的参数变化便是车轮的加速度，因此重点监控加速度的变化趋势。

轮速信号受到干扰时，最直观的现象是轮速可能会瞬间增加到非常大，这期间的角加速度和角加速度变化率会超出正常的范围，此时原始的角速度与滤波后的数值以及参考值的差别会非常大。另外，车辆实际行驶时，由于动力储备等原因，速度越高，可能达到的加速度越小，如果此时原始值与参考值偏差较大，也可以认为是轮速信号异常的表现。由此建立如下模糊规则:

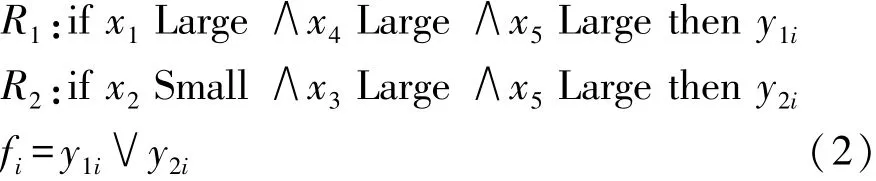
隶属度函数对计算的结果有很重要的影响，模糊逻辑中隶属度有多种，考虑到工程实际中的计算量和实时性等需求[9]，在满足计算要求的前提下，选取梯形函数作为隶属度函数，隶属度曲线示意图如图2所示。

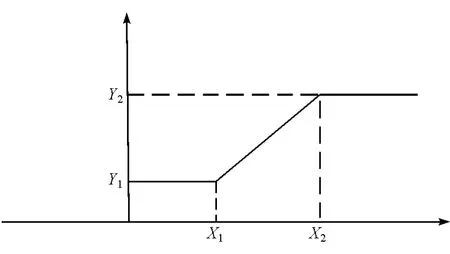
图2 模糊子集的隶属度函数

梯形隶属度函数计算公式如下。

当 Y2－Y1＞0 时:

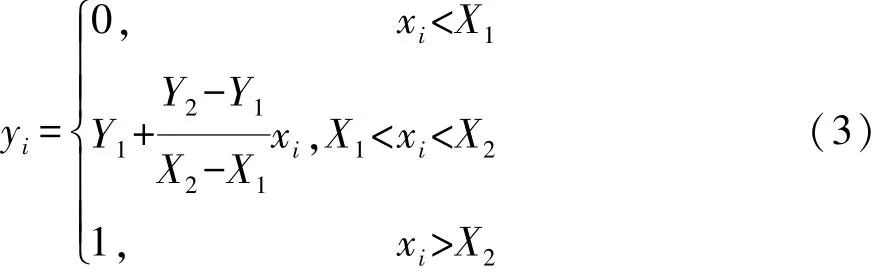
当 Y2－Y1＜0 时:

输入变量和参数如表1所示。

通过轮速信号相关变量的门限值和模糊逻辑得到轮速信号的可信程度，可信度的数值区间为[0，1]，用以表示轮速信号的可信程度，超过一定的数值，即可认为此时轮速是为异常信号。

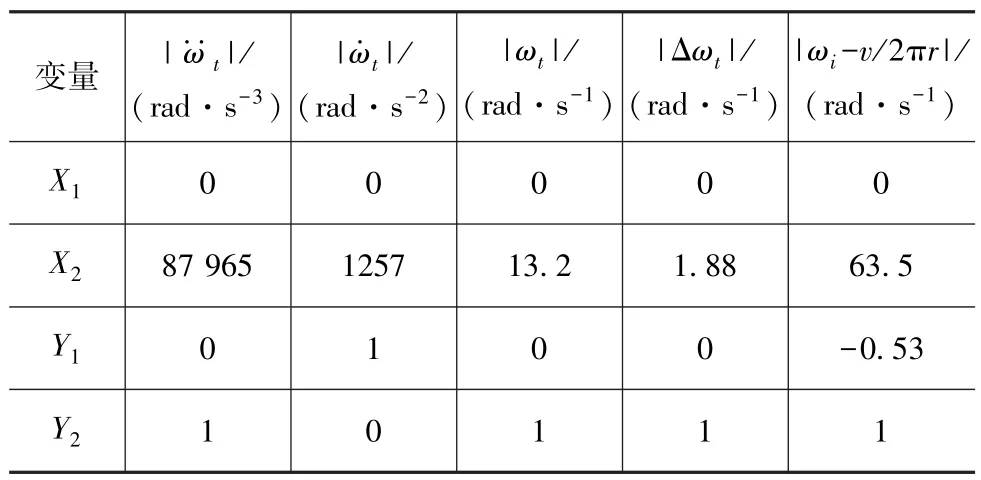
表1 输入变量和参数

5 实车试验

在实车上对所提出的参考线速度计算方法和轮速信号可信度监控算法进行验证，车辆相关参数如表2所示。依次在水平干燥水泥路面、鹅卵石路面对参考线速度进行了验证，如图3和图4所示，采集的信号来自于CAN总线。

表2 实车参数

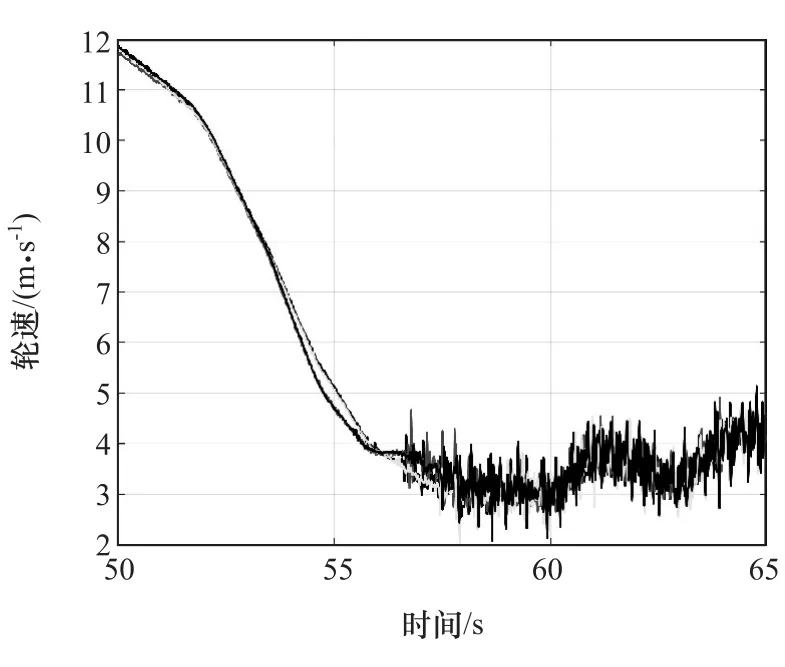
图3 轮速曲线

由图3可见，即便经过简单滤波，通过鹅卵石路面时轮速的振动仍然非常明显。由图4可见，参考线速度基本保持稳定平滑的数值，没有随着轮速信号波动而产生明显的波动，表明了该计算方法具有很好的鲁棒性。

轮速是通过统计固定间隔时间内的脉冲边缘数来计算得到，受到干扰时，会导致间隔时间内的边缘数量比实际的多。因此，通过对输入的右后车轮边缘数量信号进行人为的改动，来模拟干扰的影响。改动的方式分成两种，一种是每隔一定的周期插入边缘值，一种是持续性地插入不同数量的边缘值，两种方式对轮速信号的影响程度也不同，结果如图5～图9所示。

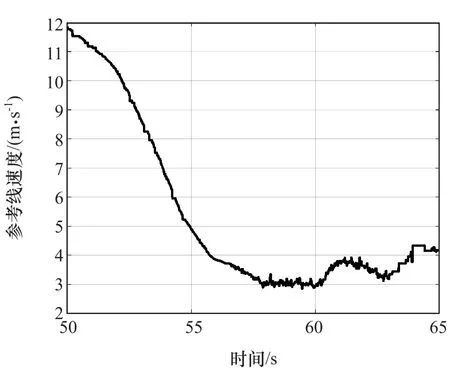
图4 参考线速度曲线

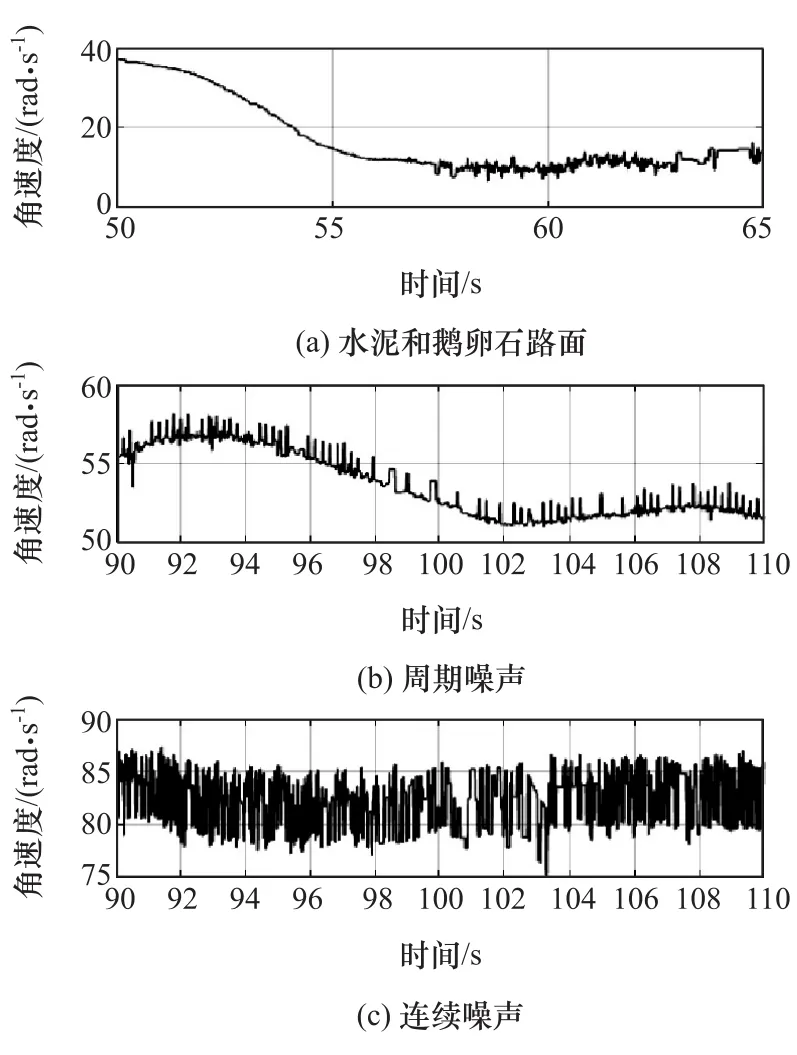
图5 右后车轮角速度

由图5～图8可以看出，手动插入边缘数量之后，相关的参数都有明显的改变，尤其是角加速度、角加速度变化率等，变化幅度非常明显。如图5中所示，受到“干扰”后，角速度成锯齿状，程度不同变化幅度不同。在图6和图7中，对应的车轮角加速度和角加速度变化率则变化更为明显，相比于实际数值，增加了2～3个数量级之多，这也是干扰信号最为明显的特征。从图8中可以看出，正常轮速的滤波值与原始数值的差别非常小，几乎相等，而异常信号的差别则非常大，远远超过了实际可能的范围。

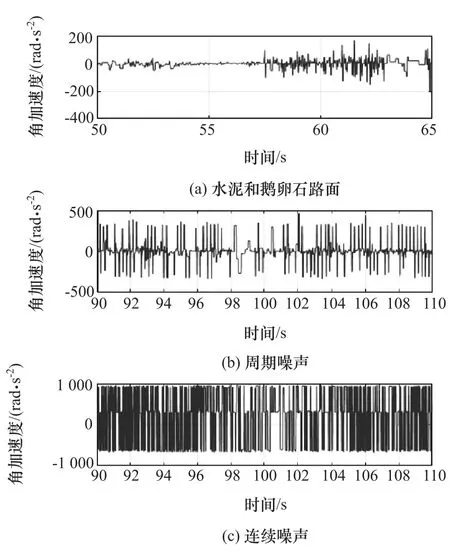
图6 右后车轮角加速度

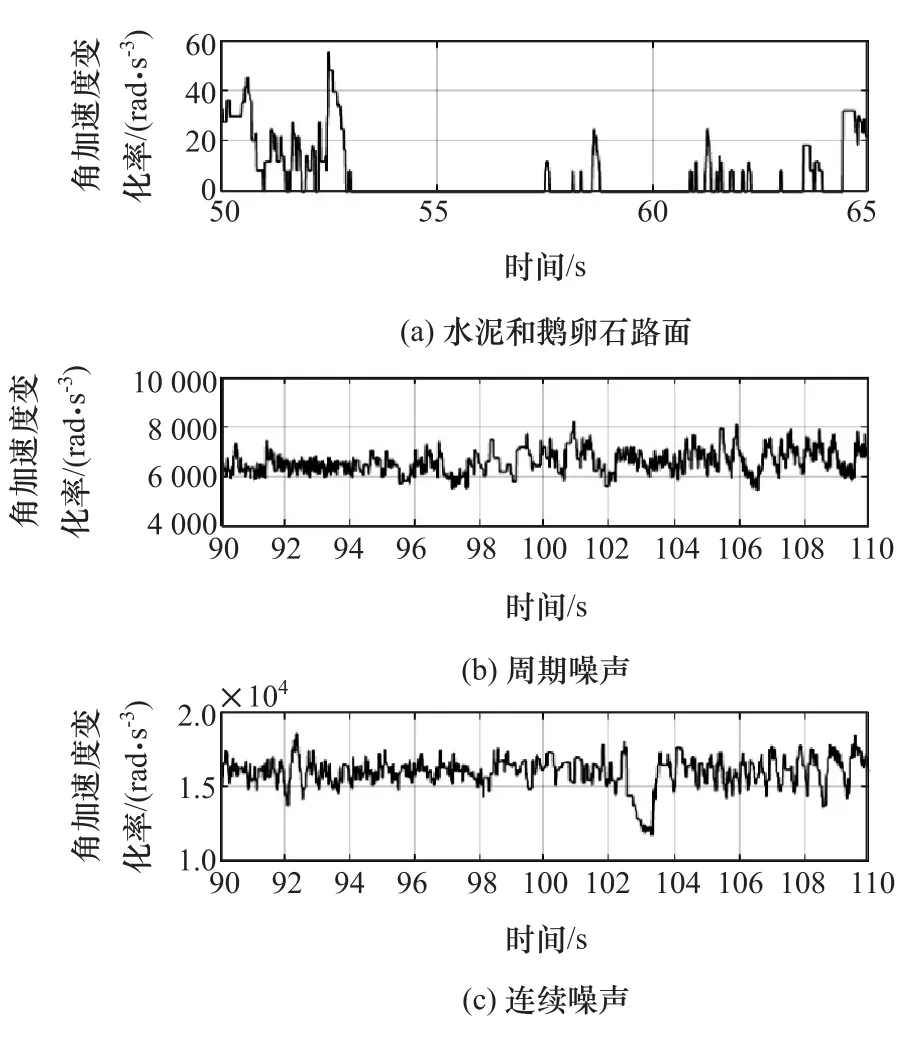
图7 右后车轮角加速度变化率

从图9得到的最终结果可以看出，在一般路面甚至颠簸路面上，虽然轮速波动比较大，但仍然是可信的，得到的异常状态也为0，表示此时信号完全可信。修改右后车轮边缘数量之后，轮速的相关参数变化程度不同，得到的可信度大小不同，但都可以认为此时轮速是不可信的。其中周期噪声由于变化幅度比较小，所以得到的可信度数值看起来像是一条直线。

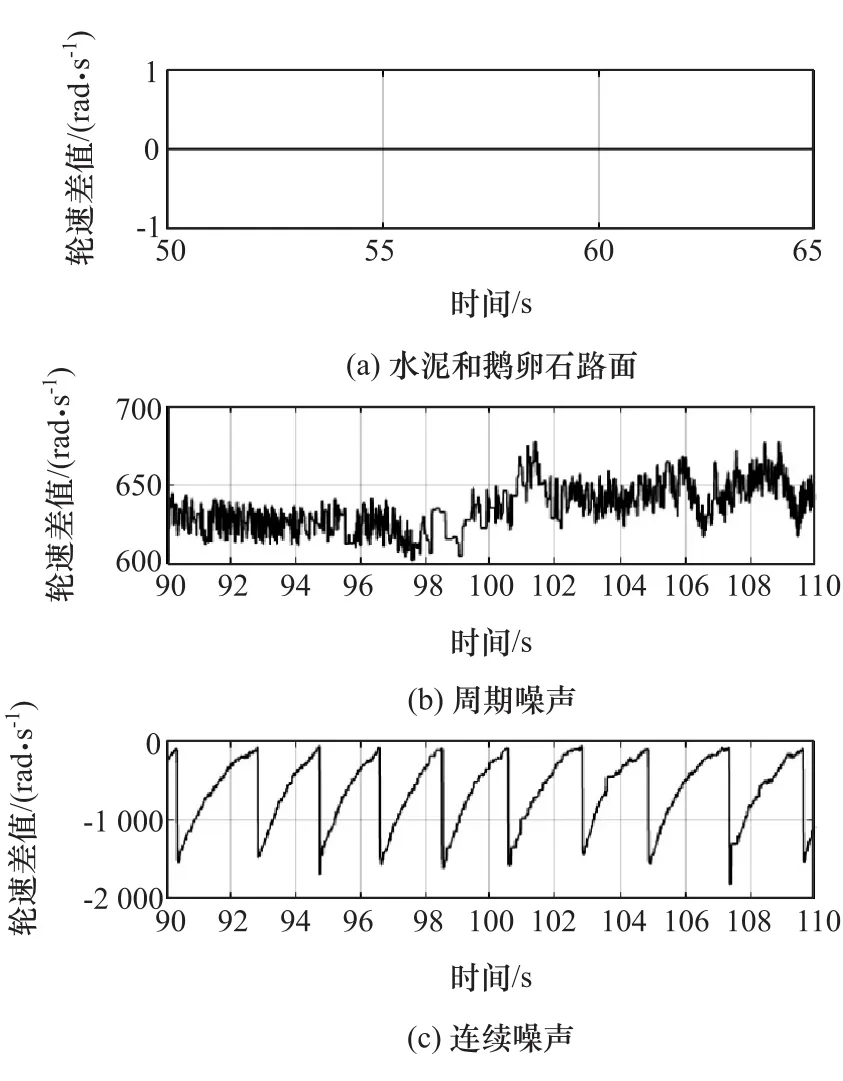
图8 右后车轮角速度原始值与滤波值的差值

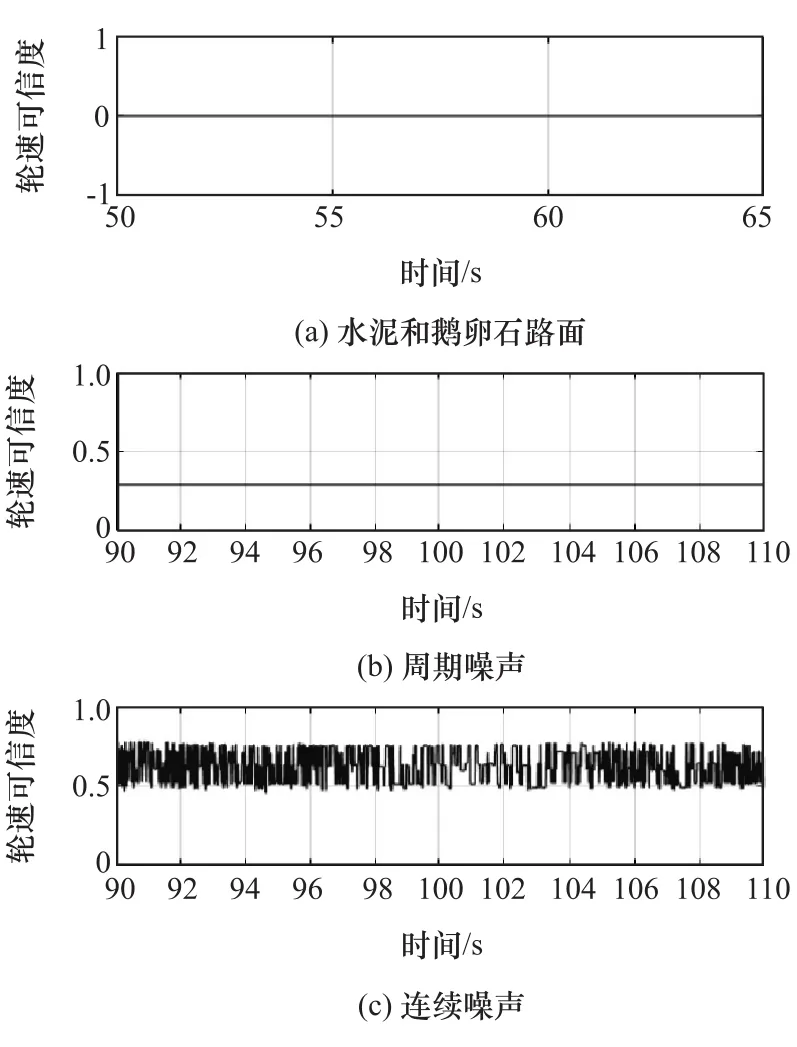
图9 右后车轮轮速信号状态

6 结论

本文中首先对不可信的轮速信号状态进行了分析，对相关参数的动力学特征进行了描述。对采集和计算得到的边缘数量、间隔时间、角速度和角加速度等参数设定固定的门限值，用以判断轮速信号是否可信。为了增强可信度监控的自适应性和鲁棒性，基于模糊逻辑对异常信号的动力学特征进行描述，用以得到轮速信号的可信度，来表示当前轮速信号的可信状态。此外，还提出了一种参考线速度的简单计算方法，作为车速信号用于模糊算法中的参数比较。

通过实车采集到的数据可以看出，所提出方法能够准确地识别出当前的异常信号，而不会对当前的正常信号进行误判。计算得到的参考线速度也是正确的，并没有随着轮速的剧烈波动而波动。

[1] HERNANDEZ W.Improving the response of a wheel speed sensor by using a RLS lattice algorithm[J].Sensors，2006，6(2):64－79.

[2] 那文波，孙坚，李璘.汽车ABS的轮速传感器系统故障类型识别方法[J].机床与液压，2008，36(b07):191－193.

[3] 厉朴，宋健，于良耀.ABS轮速信号抗干扰处理方法[J].汽车技术，2001(5):15－17.

[4] 张永辉，宋健.基于轮速特征的防抱死制动系统故障检测技术研究[J].汽车技术，2010(9):42－46.

[5] 孙尚志，陈彦夫，孙骏.ABS轮速传感器轮速信号信噪比分析研究[J].汽车零部件，2010(12):59－60.

[6] ISERMANN R.On fuzzy logic applications for automatic control，supervision，and fault diagnosis[J].Systems Man＆ Cybernetics Part A Systems ＆ Humans IEEE Transactions on，1998，28(2):221－235.

[7] VENKATASUBRAMANIAN V，RENGASWAMY R，YIN K，et al.A review of process fault detection and diagnosis:part I:quantitative model-based methods[J].Computers＆Chemical Engineering，2003，27(3):293－311.

[8] QUET P F，SALMAN M.Model-based sensor fault detection and isolation for x-by-wire vehicles using a fuzzy logic system with fixed membership functions[C].American Control Conference，2007.ACC’07.IEEE，2007:2314－2319.

[9] HIRCHE B，AYALEW B.A fuzzy inference system for understeer/oversteer detection towards model-free stability control[J].SAE International Journal of Passenger Cars-Mechanical Systems，2016，9(2016－01－1630):831－838.