基于时频图像特征约简的柴油机故障特征提取新方法∗

岳应娟，王 旭，蔡艳平，牟伟杰

（1.火箭军工程大学理学院，西安 710025； 2.火箭军工程大学五系，西安 710025）

前言

柴油机是非常复杂的机械系统，所测的振动信号属于典型的非线性、非平稳信号。基于振动信号的柴油机故障诊断的本质是模式识别问题，其中，如何从振动信号中准确提取出故障特征是问题关键。

时频分析的方法能很好地反映信号时间和频率的局部化信息，处理非线性、非平稳的振动信号时效果较好[1]。采用时频分析是将获得的时域信号转化为时频图像，时频图像提供了足够的信号故障分类信息，可通过分析图像实现故障的特征提取和智能诊断[2]。如文献[3]中通过灰度共生矩阵提取出时频图像的纹理特征；文献[4]中通过提取时频图像的三维质心与信息熵来进行设备状态识别；文献[5]中提出从时频图像的形状特征、灰度统计特征和纹理特征来综合提取特征参数的思想；文献[6]中提出对时频图像进行分割并选取特征体质心位置、面积、数目和熵作为特征参数。

然而，在利用图像分析方法对时频图像进行特征提取时，大多是提取图像的纹理特征、灰色统计特征或形状特征。这些方法都忽略了时频图像中的局部特征关系，难以区分出在不同时刻具有相同频率分量的时频图像。若将时频图像矩阵元素直接构成特征向量进行模式识别，又会由于矩阵数据维数过大带来“维数灾难”，故有必要进一步获取蕴含在时频图像内部的低维特征。非负矩阵分解算法(nonnegative matrix factorization，NMF)[7]是一种局部特征提取方法，能将存放数据的矩阵维数进行约简并保留关键信息。文献[8]和文献[9]中将NMF应用于齿轮和轴承时频图像矩阵的低维局部特征提取，取得了很好的效果。但NMF算法存在的问题是计算效率过低，一定程度上限制了其在机械故障诊断领域的应用。文献[10]中提出了一种分块非负矩阵分解算法(block NMF，BNMF)，有效提高了NMF算法的计算效率。但分块运算将时频矩阵分解为若干块小矩阵，分别运算后再进行合成，特征矩阵的稀疏性又难以保证，不利于故障类型的识别。

针对以上问题，本文中提出一种新的时频图像特征约简方法(记为C-BSNMF方法)。利用三次卷积插值法将振动谱图像进行维度压缩，通过矩阵分块计算方法结合稀疏非负矩阵分解，将压缩后的图像矩阵分解为一系列代表了不同时间和频率范围内的时频分量的基图像的线性组合，直接提取出时频图像中的故障特征。实验验证表明，该方法能够准确地提取出柴油机气门机构的故障特征，并且大幅提高了特征提取的计算效率。

1 分块稀疏非负矩阵算法

矩阵的稀疏计算由向量的稀疏度计算推演而来。给定一个向量x∈Rn，文献[11]中提出使用L1范数与L2范数之比作为该向量的稀疏度测度:

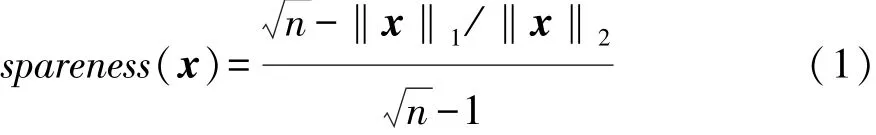
一个向量的稀疏度介于0～1之间。图1给出了对稀疏度的直观理解，稀疏度越大，特征量就越少，主要特征就越明显。

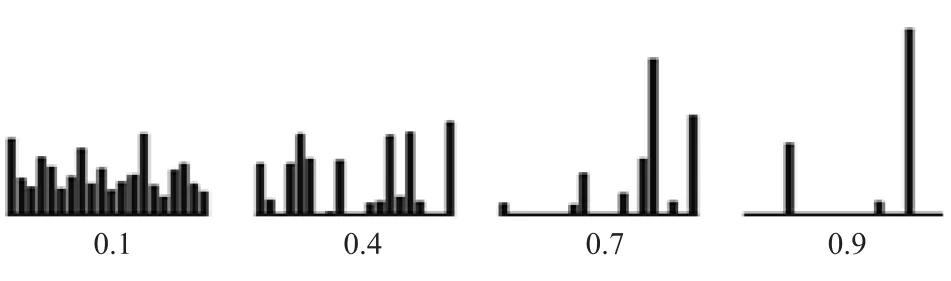
图1 不同稀疏度下的稀疏向量

1.1 稀疏非负矩阵分解

SNMF是在稀疏编码和NMF相结合的基础上提出的[12]。SNMF通过对NMF中的基矩阵或系数矩阵施加稀疏约束来进一步减少约简后信息的冗余。SNMF的本质是一种矩阵分解和投影技术，其基本原理如下。

对于非负观测矩阵V，找到两个合适的非负矩阵因子W和H，满足:

式中:n为数据样本的维数；m为集合中数据样本的个数；r为特征维数，一般情况下，r远小于n且满足f(i＋u，j＋v)。

为了描述V≈W·H的近似效果，利用矩阵V与W·H间的K－L散度作为近似误差，在NMF的基础上加入了稀疏惩罚项α对应的目标函数:

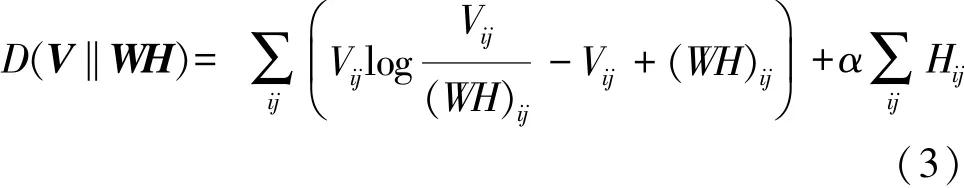
其对应的优化问题为

根据此目标函数，文献[11]中推导出了W和H的更新规则，推导过程参照经典的NMF基本算法，也即当α＝0时SNMF退化为经典NMF算法。W和H的迭代公式为

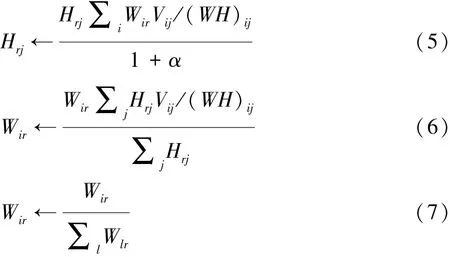
1.2 分块稀疏非负矩阵分解

分块计算的思想最早在文献[13]中提出。虽然SNMF算法符合“局部构成整体”的认知规律，但它开始是将矩阵看成整体而非局部之和。如果从开始就将矩阵视为“整体为局部之和”，对矩阵分块各自分解后再将分解后的各子块按原序拼接，而分解过程中矩阵的各块之间并不运算，则可以有效提高算法的收敛性能。本文中将这种分块运算方法应用于SNMF，提出一种分块稀疏非负矩阵分解算法(block SNMF，BSNMF)，其基本原理如下。

将非负观测矩阵按列平均分为一系列块矩阵的形式 Vm×n＝[V1V2… Vb]，其中 Vi∈Rm×n0，b 为分块数，n0＝n/b。对每一个块矩阵按照式(5)～式(7)进行迭代运算，得到相应的基矩阵和系数矩阵。

式中r0＝r/b为块矩阵的特征维数。按照式(9)和式(10)将分解得到的基矩阵和系数矩阵按原顺序进行合成，即可得到原非负观测矩阵的基矩阵和系数矩阵。

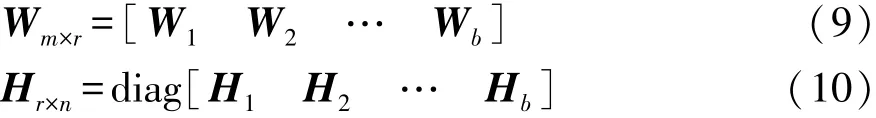
1.3 算法计算复杂度分析

以算法中的乘法次数来表征计算复杂度。由式(5)，在矩阵H的迭代计算中，SNMF算法的计算复杂度为

由式(6)和式(7)，在矩阵W的迭代计算中，SNMF算法的计算复杂度为

一次迭代过程SNMF算法的计算复杂度:

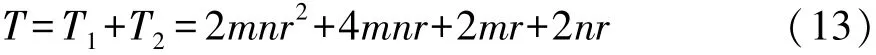
对于本文中所提出的BSNMF算法，在Hi与Wi的迭代计算中，计算复杂度分别为

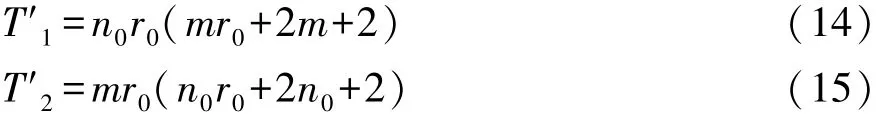
则一次迭代中BSNMF算法的计算复杂度为

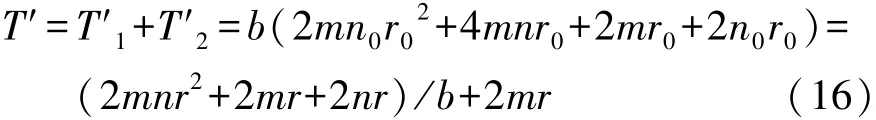
比较式(13)与式(16)可知，BSNMF的计算量要比SNMF的计算量要小得多。

2 三次卷积插值法

虽然BSNMF算法可有效减少SNMF算法的计算量，但由于分块计算时要满足r0＝r/b，使r0为正整数，故分块数b也要满足(m＋n)b＜mn，对于较高维度的振动谱图像来说，算法耗时仍旧很长。所以，考虑利用三次卷积插值法对每个振动谱图像进行维度压缩。

三次卷积插值[14]又称为立方卷积插值，其本质是利用采样点的周围16个点的灰度值作三次内插运算，如图2所示。

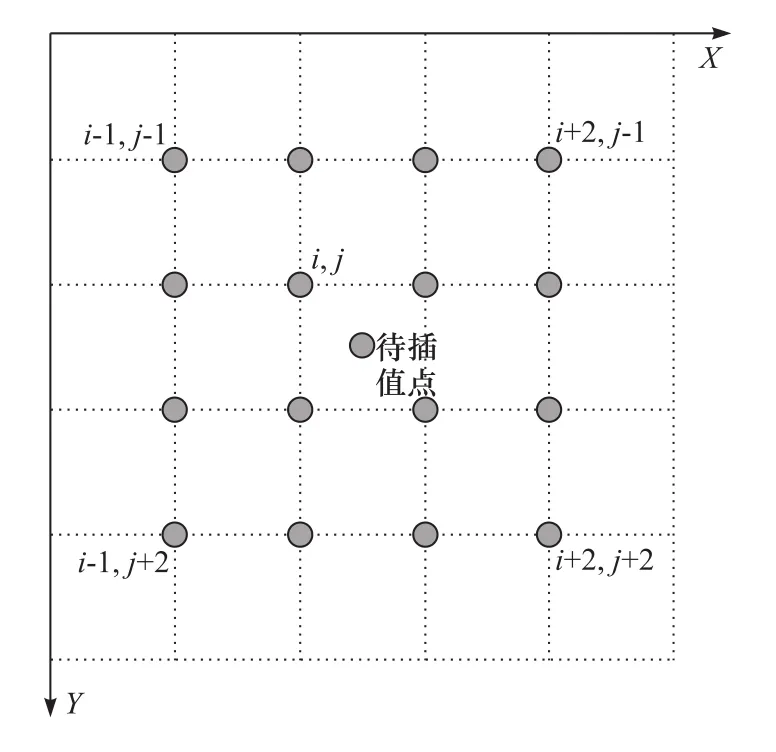
图2 待插值点与16个邻近点排布

由连续信号采样定理可知，若对采样值用插值函数sinc(w)＝sin(w)/(w)进行插值，则可准确地恢复原函数，得到采样点间任意点的值。三次卷积插值法实质上就是利用一个三次多项式来近似理论上最佳插值函数S(w):

目标值 f(i＋u，j＋v)可由如下插值公式得到:

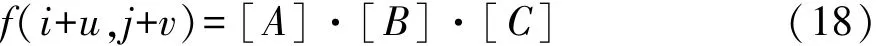
其中:

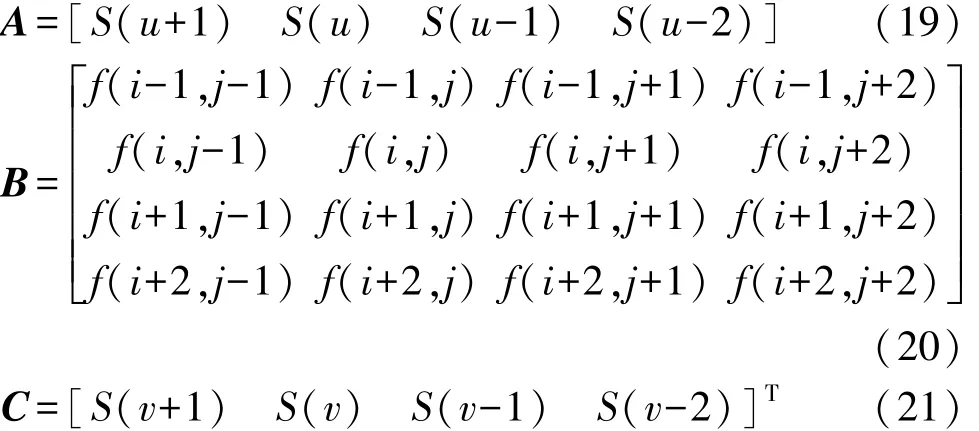
三次卷积插值法带有边缘增强的效果，能较好地保持图像的细微结构。因此利用三次卷积插值算法与BSNMF相结合，能够对高维的振动谱图像矩阵进行有效的特征约简，同时具有较高的执行效率，使算法的泛化性能得到进一步增强。

3 柴油机气门故障特征提取实例

3.1 实验流程

基于时频图像特征约简方法进行柴油机故障特征提取和效果验证的流程如图3所示。

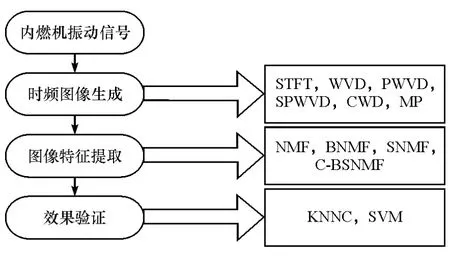
图3 故障特征提取及效果验证流程

实验对比方法设置如下。

(1)时频图像生成，分别用线性时频分析中具有代表性的短时傅里叶变换(STFT)和非线性时频分析中的魏格纳分布(WVD)、伪魏格纳分布(PWVD)、平滑伪魏格纳分布(SPWVD)、乔威廉姆斯分布(CWD)以及参数化时频分析方法中利用匹配追踪算法(MP)与WVD相结合生成的时频分布，共6种时频分析方法产生振动谱图像来验证本文方法。以工况1的时频分布为例，用6种分析方法生成时频图像，为便于进一步的图像分类与识别，将图像转化为维度为420×560的灰度图的形式，如图4所示。

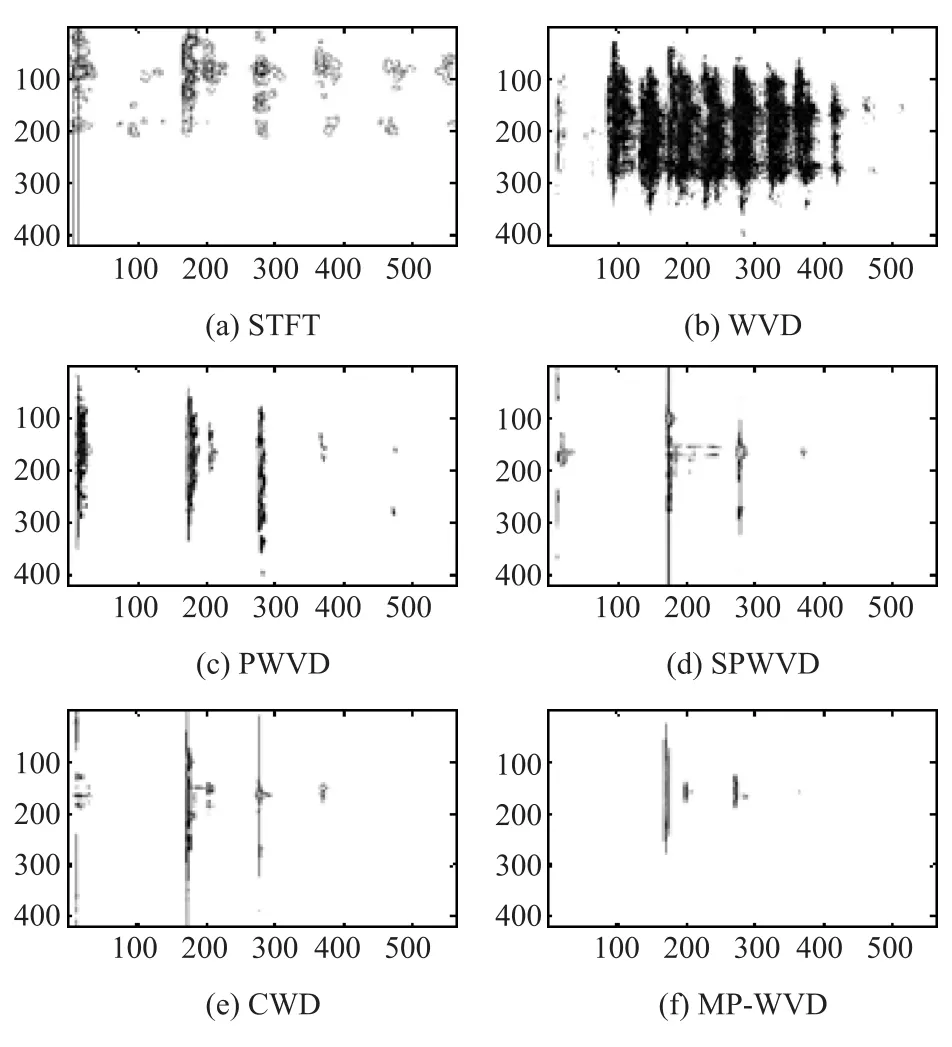
图4 工况1的6类时频表示振动谱图

STFT描述的是信号的频谱随时间变化的情况，分辨率自适应性差；其余5类分布都是描述的信号的能量密度随时间变化的情况，WVD具有最佳的时频分辨率，但是交叉干扰项严重，PWVD，SPWVD和CWD是通过加窗或引入核函数的方法来抑制WVD的交叉干扰项，但都不可避免地降低了时频分辨率；利用MP算法将信号分解为一系列单分量原子，再叠加每个原子分量的WVD，得到的时频分布保持了WVD良好的时频聚集性，并且消除了WVD中交叉项的干扰。

(2)特征提取，本文方法运用三次卷积插值算法对时频图像矩阵进行维度压缩，用分块稀疏非负矩阵分解算法对时频表示特征约简(C-BSNMF特征提取)。将这种方法与现有的NMF，BNMF和SNMF 3种方法进行对比。以特征提取时间来表征计算时间复杂度，对比方法的计算效率；以分类器的识别率来表征特征提取效果，对比方法的特征提取性能。分类器分别选择模式识别性能较为稳定的K-最近邻分类器(KNNC)和在处理小样本、非线性数据时效果较好的支持向量机(SVM)。

3.2 实验设置

以6135型柴油机为研究对象，实验平台由柴油机、传动轴、电机和控制台4部分组成，如图5所示。取柴油机第2缸盖表面振动信号对柴油机进行故障诊断，采样频率25kHz，转速为1 500r/min，测试过程中，柴油机空载运行。共设置了4种气门间隙状况，具体情况如表1所示。其中0.06，0.3和0.5mm分别对应气门间隙过小、正常和过大，开口表示在气门上开4mm×1mm孔来模拟严重漏气故障。共采集柴油机气门4种故障状态下各60组振动信号样本，总计240个。

图5 实验平台

3.3 实验工况分析

根据6135型柴油机的工作原理可知，引起缸盖振动的原因主要是气体燃烧时产生的爆压，气门落座撞击和排气门开启所引起的气流冲击等，邻缸的各种振动激励源也会对缸盖的振动产生较大影响[15]。图6示出进排气门开闭和点火时刻与曲轴转角的关系。进气门开启的角度在排气上止点前20°CA附近，关闭的角度在进气下止点后48°CA附近；排气门开启的角度在做功下止点前48°CA附近，关闭的角度在进气下止点后20°CA附近；柴油机在0°CA点火。图7和图8给出了4种工况下振动信号的时域和功率谱图像。

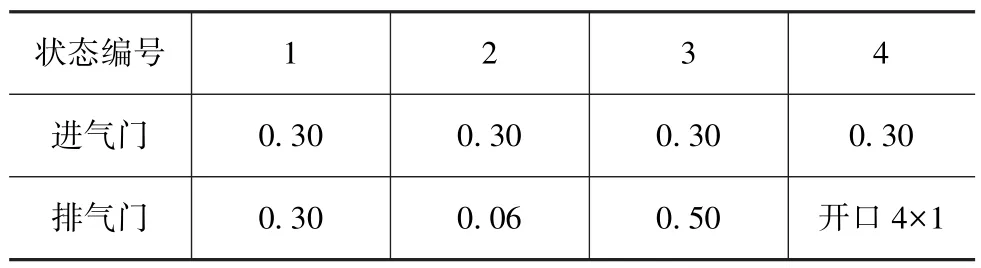
表1 4种实验工况设置 mm

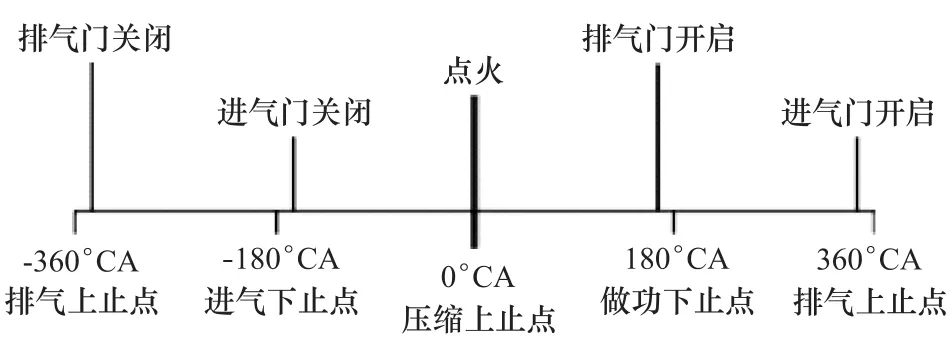
图6 柴油机燃烧和气门开闭转角图

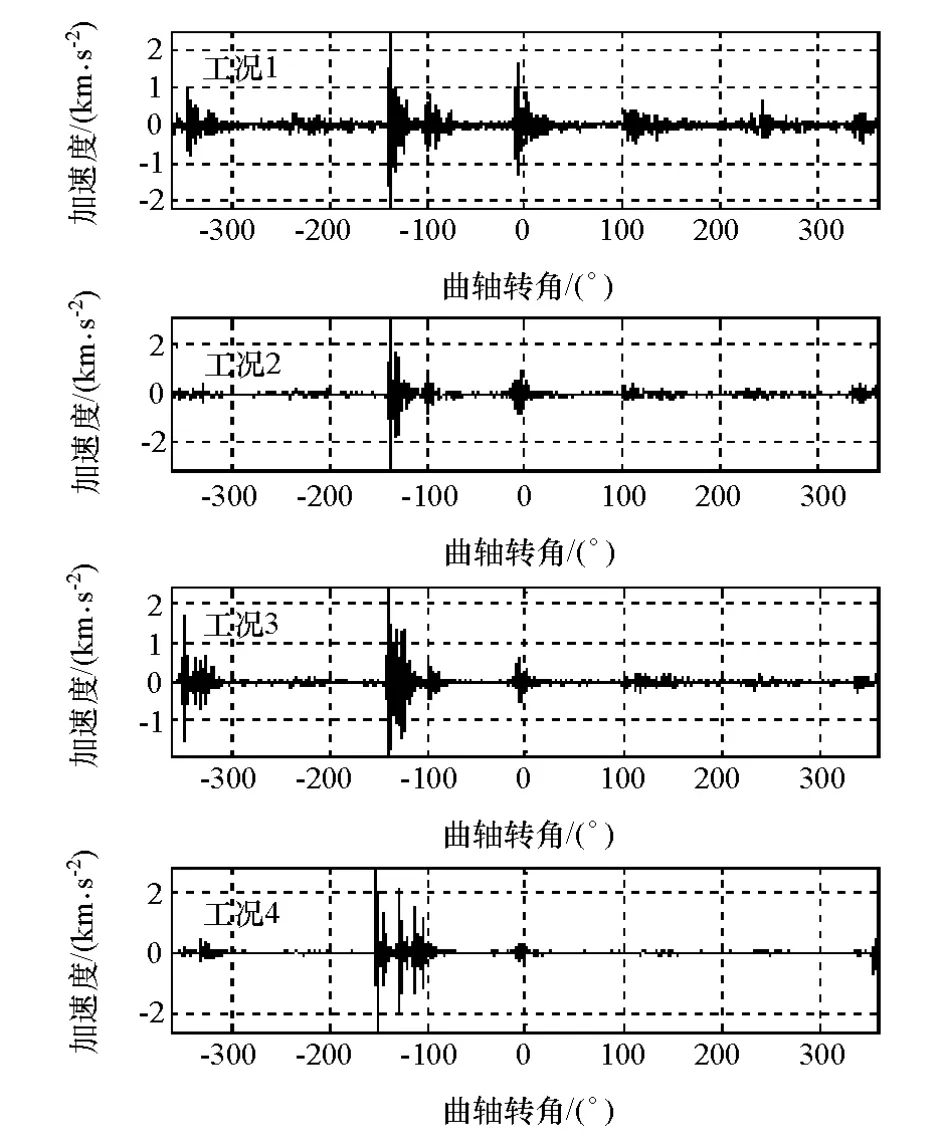
图7 4类工况时域波形

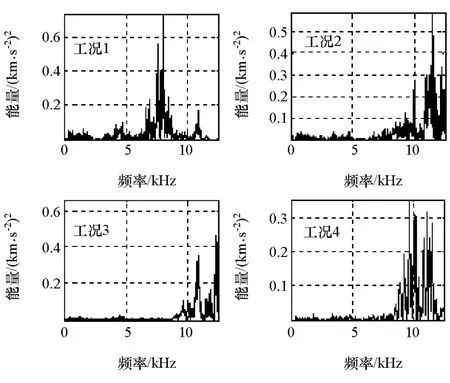
图8 4类工况功率谱图

从图7的时域波形图可以看出，气门间隙状态的变化对振动信号有较大的影响，主要体现在几个剧烈振动分量产生与消亡的时刻发生了变化，各剧烈振动分量的幅值变化也特别明显。比较图8中4种状态下的功率谱图可以看出，在正常状态下，缸盖振动信号的能量主要集中在6.5～8.5kHz之间的高频区域。在非正常状态，也即气门间隙出现故障时，主要能量向更高的频段移动，一般集中在8.5～12.0kHz之间。

3.4 实验结果与分析

将每种工况的60组振动信号中随机选出30组信号组成训练样本，其余信号组成测试样本。第3.1节中所述6类时频表征方法生成图像的维度为420×560，利用三次卷积插值算法对时频矩阵进行0.1倍压缩，得到维度为42×5642×56的6类时频矩阵，如图9所示。由于实际应用中估计低维空间维数R十分困难，且依据应用目的不同维数设置准则也存在差别[16]。同时，受分块计算算法的限制，根据实际的矩阵维度情况，以16为步长，R从16到128取值，在不同的特征维数下分别迭代计算，并限定总的迭代次数为160(分块运算时每一个块矩阵迭代10次)。

表2给出了4种算法对WVD时频图像进行特征提取的计算效率，均不包含图像载入时间。实验环境为Matlab R2012b，AMD A8处理器，CPU主频1.90GHz，内存为4GB，操作系统为Windows 7。

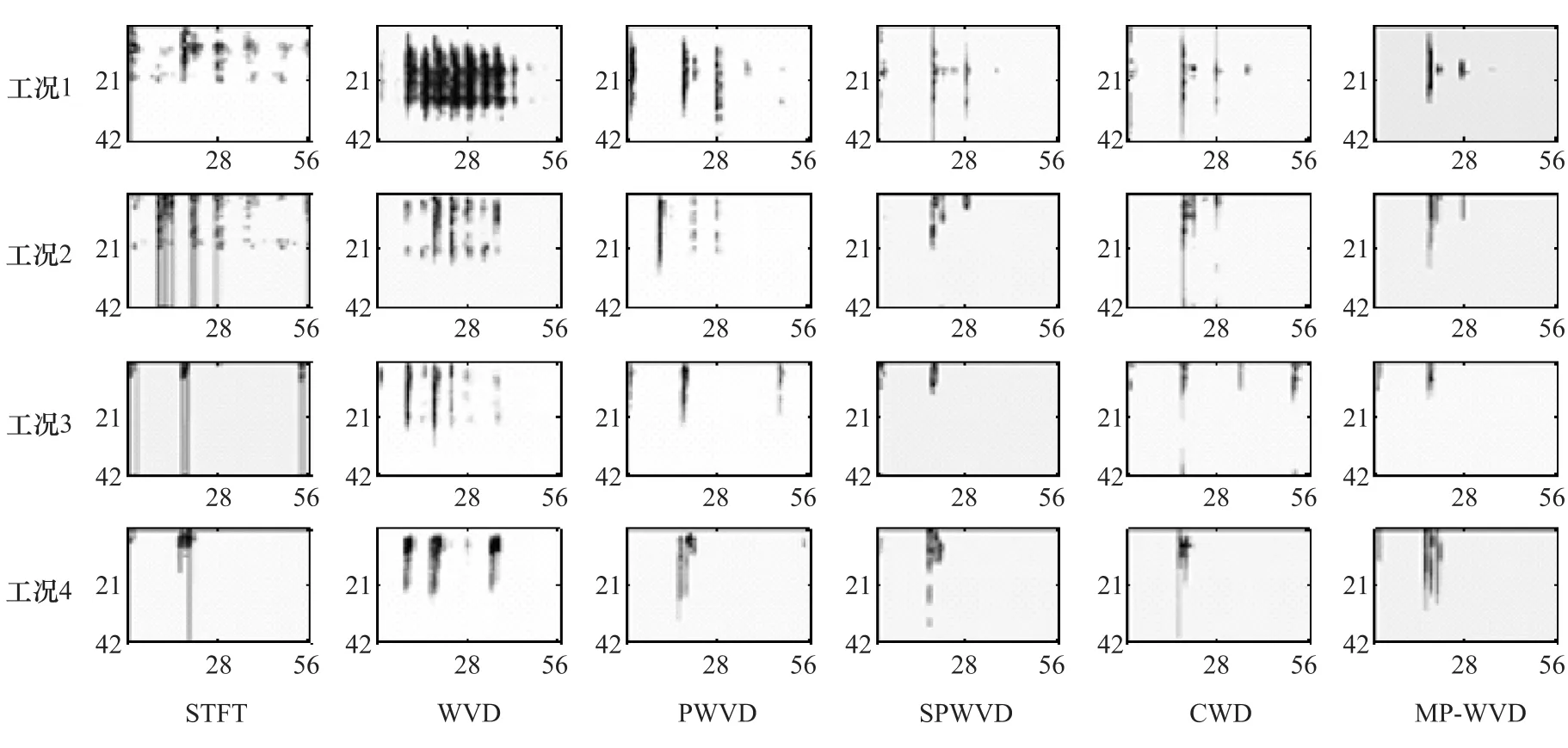
图9 利用三次卷积插值算法压缩后的6类时频图像

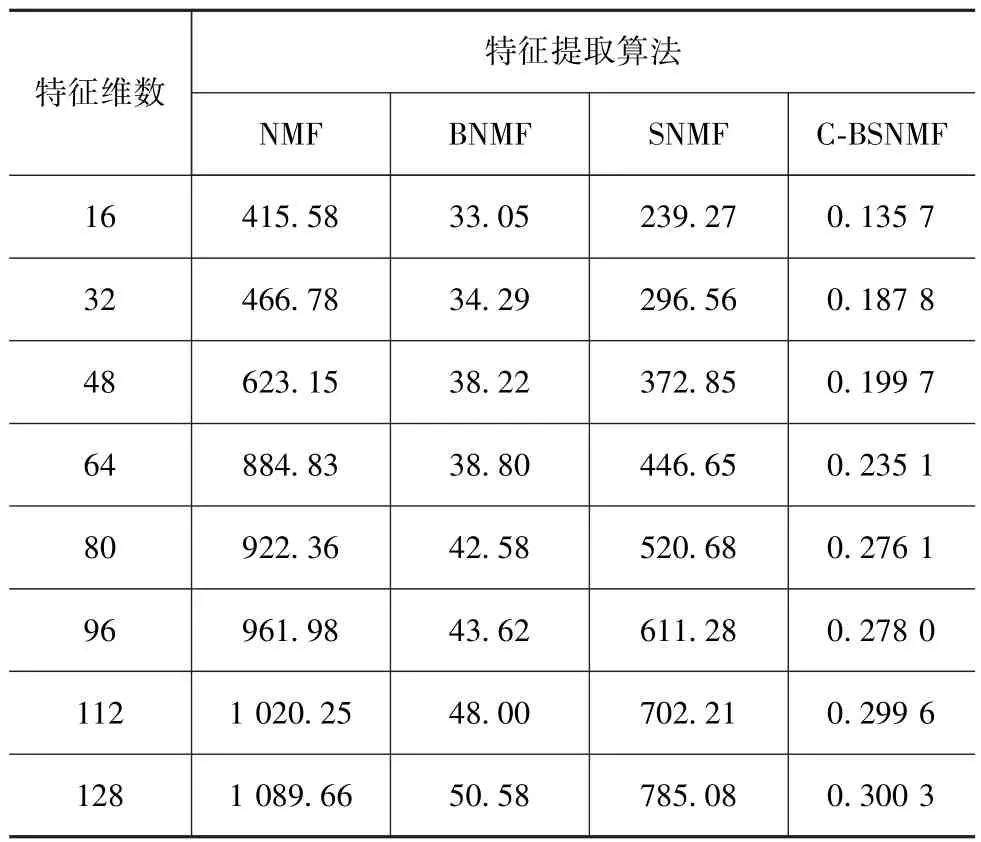
表2 4种方法对WVD时频特征提取的耗时情况s

由表可见:从计算耗时的角度分析，纵向来看，用同一种矩阵分解方法时，计算耗时随选取的特征维数的增大而增加；横向来看，分块计算的方法能够提高运算效率，分块数为16时，BNMF的运算效率较NMF提高了13倍左右，印证了第1.3节计算复杂度的推导。通过运用三次卷积插值法对时频图像进行维度压缩，本文中所提的 C-BSNMF方法在SNMF的基础上，运算速度提高了1 500～2 000倍。

表3给出了不同特征维数下，运用KNNC与SVM分别作为分类器，4种方法对WVD时频图像特征提取的识别效果。将生成的6种振动时频图像分布用4种约简方法进行处理，并用KNNC和SVM两种分类器进行模式识别，得到不同时频图像应用不同约简方法的识别结果，如图10所示。

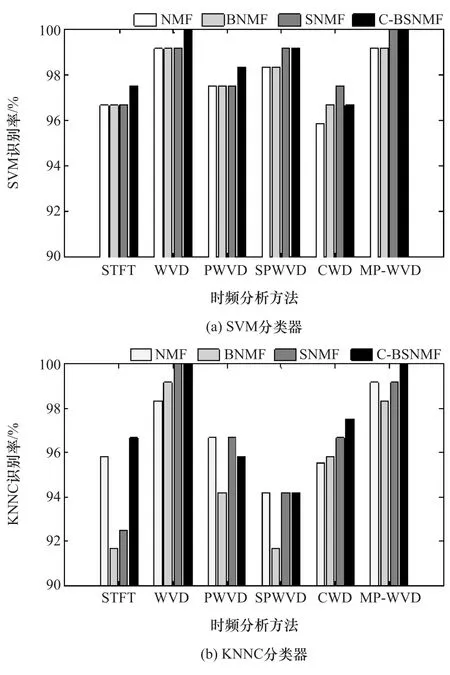
图10 6类时频图像识别正确率比较

由图10可以看到，对于同样的一批振动数据，在同样的分类指标下，采用的时频分析方法不同，其识别正确率也不一样。其中，以MP-WVD和WVD得到的时频分布的识别正确率相对较高，最高识别率都达到了100%，而STFT和CWD分布的识别正确率相对较低。这表明，时频分析方法对识别结果有一定的影响。WVD分布具有最好的时频聚集特性，MP-WVD算法得到的时频分布是将单分量原子信号WVD线性叠加，也保持了最好的时频聚集特性。能量本身是一种二次型的表示，这种描述具有更好的边缘特性和有限支撑性质。这种良好的时频聚集特性使各状态间的差异性相对更为明显。不论是用SVM还是KNNC作为分类器，都能保证很高的识别正确率。相比下，PWVD，SPWVD和CWD 3种分布虽然抑制了WVD分布的交叉项的干扰，但也降低了时频分布的聚集性能，利用本文方法得到的特征提取效果反而不如WVD。

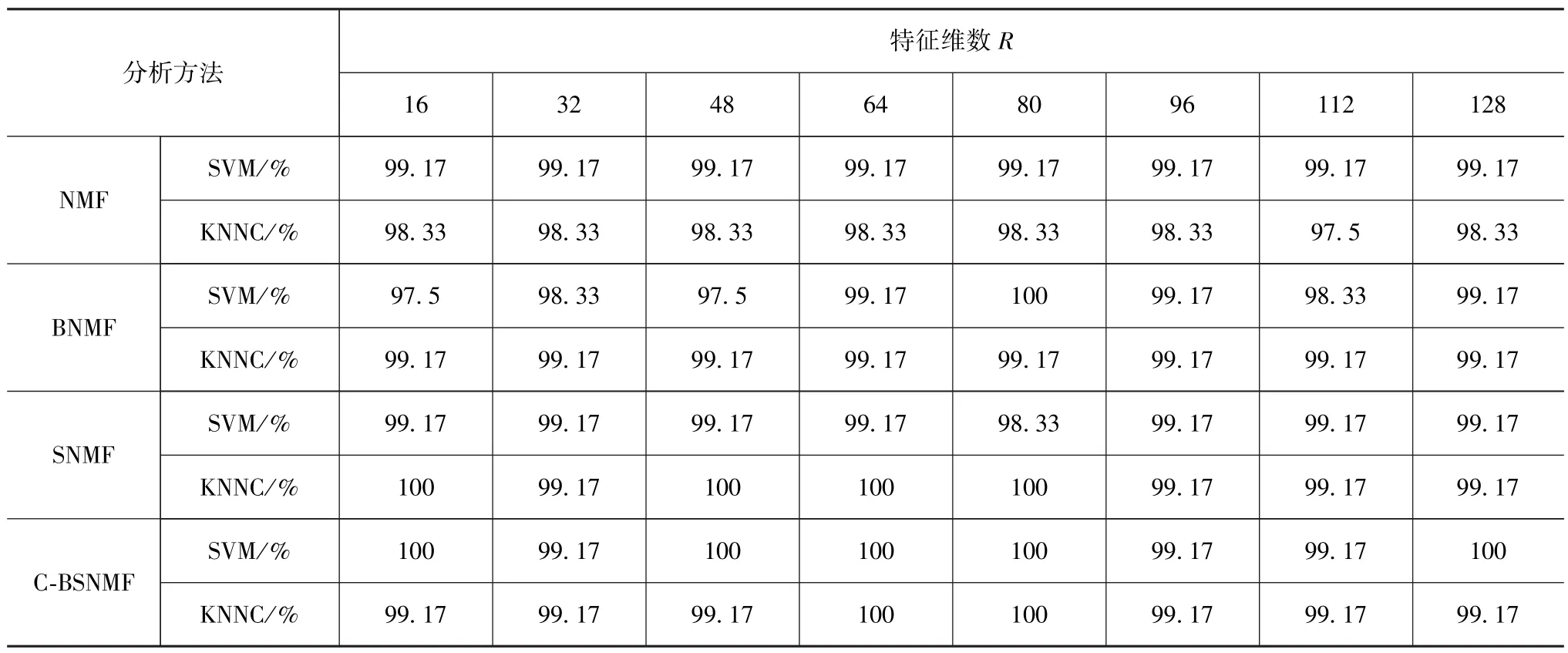
表3 4种方法对WVD时频图像特征提取效果对比

对比分析NMF，BNMF，SNMF和 C-BSNMF 4种方法的特征提取效果。以SVM作为分类器时，可以看到，本文所提方法C-BSNMF的效果最优(采用CWD时频分布时除外)；以KNNC作为分类器时，本文所提方法的效果也最优(采用PWVD时频分布时除外)，充分说明了本文方法更易获取蕴含在高维时频矩阵内部的低维特征。

4 结论

(1)将基于时频图像的特征约简提取方法应用于6135型柴油机气门机构的故障自动诊断中，取得了较高的识别正确率。说明该方法对于柴油机的复杂非平稳振动信号的时频特征提取是有效的。

(2)结合三次卷积插值法与分块稀疏非负矩阵分解算法的特征约简方法在低维特征提取效果和计算效率上较现有的几种特征约简方法有很大程度的提高，为非线性、非平稳信号的特征提取提供了一种有效的方法。

(3)利用时频图像特征约简的方法提取柴油机气门机构故障特征时，基于匹配追踪算法的时频分布和魏格纳时频分布的特征提取效果要优于其他几种时频表示方法，说明利用本文时频图像良好的时频聚集特性能使特征提取效果更优。此结果对时频分析方法的研究方向有一定的借鉴意义。

[1] 张俊红，王健，毕凤荣，等.基于EMD和时频分析的低振动机体结构优化研究[J].振动与冲击，2014，33(3):117－121.

[2] FENG Zhipeng， LIANG Min， CHU Fulei.Recent advances in time-frequency analysis methods for machinery fault diagnosis:a review with application examples[J].Mechanical Systems and Signal Processing，2013，38(1):165－205.

[3] 刘建敏，刘远宏，江鹏程，等.基于包络S变换时频图像提取齿轮故障特征[J].振动与冲击，2014，33(1):165－169.

[4] 李宏坤，周帅，黄文宗.基于时频图像特征提取的状态识别方法研究与应用[J].振动与冲击，2010，29(7):184－188.

[5] 蔡艳平，李艾华，何艳萍，等.基于振动谱时频图像特征及SVM参数同步优化识别的内燃机故障诊断[J].内燃机学报，2012，30(4):377－383.

[6] 蔡艳平，李艾华，王涛，等.基于时频谱图与图像分割的柴油机故障诊断[J].内燃机学报，2011，29(2):181－186.

[7] LEE D D，SEUNG H S.Learning the parts of objects by non-negative matrix factorization[J].Nature，1999，401(21):788－791.

[8] 李宏坤，陈禹臻，张志新，等.基于非负矩阵分解与主元分析的时频图像识别研究方法[J].振动与冲击，2012，31(18):169－172.

[9] LI Bing， ZHANG Peilin， TIAN Tao， et al.A new feature extraction and selection scheme for hybird fault diagnosis of gearbox[J].Expert Systems with Applications，2011，38(8):10000－10009.

[10] 潘彬彬，陈文胜，徐晨.基于分块非负矩阵分解人脸识别增量学习[J].计算机应用研究，2009，26(1):117－120.

[11] HOYER P O.Non-negative matrix factorization with sparseness constraints[J].Journal of Machine Learning Research，2004(5):1457－1469.

[12] LIU Weixiang， ZHENG Nanning， LU Xiaofeng.Non-negative matrix factorization for visual coding[C].Washington:Proc of IEEE Int Conf on Acoustics， Speech and Signal Processing，2003:293－296.

[13] SRA S.Block-iterative algorithms for non-negative matrix approximation[C].Eighth IEEE International Conference on Data Mining，2008:1037－1042.

[14] ZHOU D，SHEN X，DONG W.Image zooming using directional cubic convolution interpolation[J].IET Image Processing，2012，6(6):627－634.

[15] WANG Qinghua， ZHANG Youyun， CAI Lei， et al.Fault diagnosis for diesel valve trains based on non-negative matrix factorization and neural network ensemble[J].Mechanical Systems and Signal Processing，2009，23(5):1683－1695.

[16] GAO Huizhong， LIANG Lin， CHEN Xiaoguang， et al.Feature extraction and recognition for rolling element bearing fault utilizing short-time Fourier transform and non-negative matrix factorization[J].Chinese Journal of Mechanical Engineering，2015，28(1):96－105.