最优加权随机汇池网络的估计性能研究

， ，，，

(青岛大学 a.复杂性科学研究所；b.电子信息学院，山东 青岛 266071)

0 引言

信息处理中经常面临两种难题：随机噪声和有损压缩。随机噪声经常被视为信号处理的不利因素加以抑制，有损压缩是允许信息压缩过程中损失一定的信息，而这部分信息通常是冗余的或不相关的[1]。Zozor和McDonnell通过随机网络方法可以同时实现有损压缩和降噪，并在该领域进行了一系列研究，提出了随机汇池网络概念[2-4]。随机汇池网络是一种由多个并联传感器组成并接收同一个信号源馈入的网络，输入信号和测量过程噪声同时被传感器非线性压缩，最后汇集至一个物理信道，网络输出为一维的参数估计响应，此网络也是冗余信息、有损压缩和噪声相互作用的一种网络。随机汇池网络广泛地存在于噪声数模转换器[3,5]，受体细胞、平行神经元等生物传感处理[6-8]、纳米电子[9]、通信网络[10]等系统中。Zozor和McDonnell等详细研究了随机汇池网络中噪声引起的超阈值随机共振现象[2-4]，即随机噪声能够使信号传输质量或某些性能指标提高的一种反直觉效应。由于随机汇池网络本质上是一种随机信号估计器，因此超阈值随机共振现象在信号估计、检测和传输等领域都得到了广泛的关注，在生物医学方面的耳蜗植入研究[16]、非线性检测器[17]以及模数转换电路设计[18-19]等方面取得了非常有实际应用价值的进展。

随机汇池网络的研究[2-4,11-19]局限于平稳的随机信号和噪声环境，其译码方案需要知道输入信号的先验知识和噪声的统计性能。而实际信号处理中，由于输入信号的统计特性一般是未知的，这给随机汇池网络的应用研究带来巨大困难。本文建立一种更加广泛的随机汇池网络模型，网络节点并不局限于阈值型激活函数，同时考虑权系数和噪声对信号译码性能的影响，以均方误差[19]作为性能指标，求得此模型的最优权系数[21]，并进一步以噪声强度为变量进行优化，推导了自适应最优权系数以及估计信号与真实信号之间均方误差的理论表达式。同时，考虑到统计信息在实际工程中经常是未知的，本文给出了基于观测数据的最优权向量和均方误差的最小二乘估计算法。理论和实验都验证了随着随机汇池网中节点数目的增加，该网络的估计性能随之提高，且均方误差不断逼近最小均方误差估计器，充分反映了随机噪声优化能力和自适应最优加权随机汇池网络的估计性能，在实际的非线性信号估计中具有重要的应用价值。

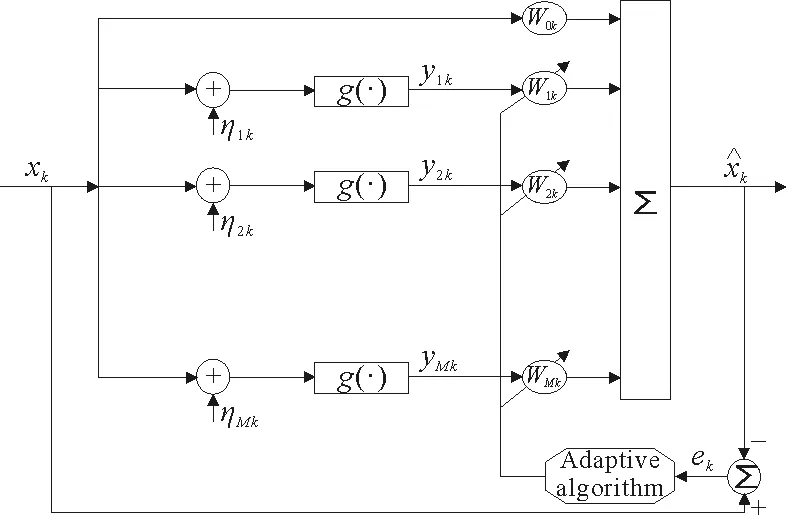
图1 博弈主体间的概念模型Fig.1 Model of adaptive weighted stochastic pooling network

1 模型与方法

1.1 随机汇池网络模型

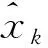
1.2 理论分析

1.2.1 最优权向量和均方误差

将权系数wi,k表示为wk=w1,k,w2,k,…,wM,kT，列向量yk=y1,k,y2,k,…,yM,kT来表示系统函数g处理的随机输出信号。那么，随机汇池网络的输出可以表示为

(1)

(2)

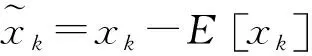
(3)

(4)

代入式(3)得到有关权向量的最小均方误差

(5)

由于本文均考虑当前时刻k且考虑稳态的输入信号和网络噪声，因此下面理论分析将k省略。在输入输出的相关向量为Pxy中Exyi可以计算为

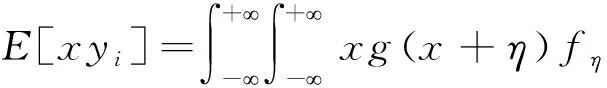
(6)

协方差矩阵Cyy矩阵中的对角元素Cii可以表示为

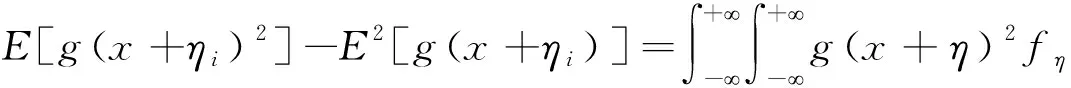
非对角元素Cij可以表示为

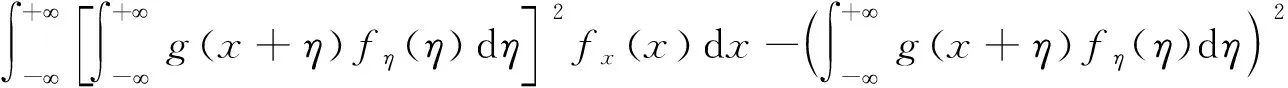
Cyy=QΛQH

(7)

那么最优权向量可表示为

(8)

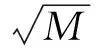
(9)

(10)

当M=情况下，均方误差可以计算为

(11)

1.2.2 网络节点数对模型性能的影响

Cyy为正定对称矩阵，可被唯一地分解为一个下三角矩阵、一个对角阵和一个上角矩阵的积，即Cyy=LDLH，L是一个单位下三角矩阵，D=diagξ1,ξ2,…,ξM为一个对角阵，其元素必为正实数。考虑到网络节点数对矩阵阶数的影响，对LDLH分解以阶数递归的形式进行分析，为方便接下来的论证，令C=Cyy，P=Pxy。将网络节点数由m增加为m+1，相关矩阵

(12)

(13)

(14)

LmDmkm=Pm

(15)

可得km同样具有最佳嵌套性质。由式(15)得出最小均方误差

(16)

由于矩阵L和矩阵D具有最佳嵌套性质，式(16)可写为

(17)

由式(17)可得，由于ξm>0，随着模型节点数增大，使最小均方误差减小，得到更好的估计精度。

2 实验分析

在实际信号处理中，需要考虑到信号或噪声的先验知识可能是未知的情况，因此对于Pxy和Cyy的理论值需要利用观测数据进行估计。在可以获得充分多的输入信号xk和节点输出yi,k的观测数据的条件下，本文对自协方差Cyy中每一元素估计如下

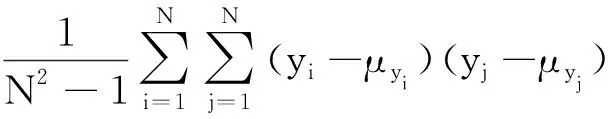
(18)

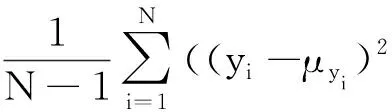
(19)

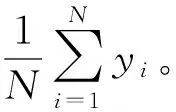
(20)

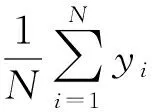
实验选取输入信号xk服从高斯分布，其均值为零，标准差σx为1。噪声ηi选用均值为零，标准差ση可调谐的高斯白噪声，并且所有节点取相同的阈值函数

(21)

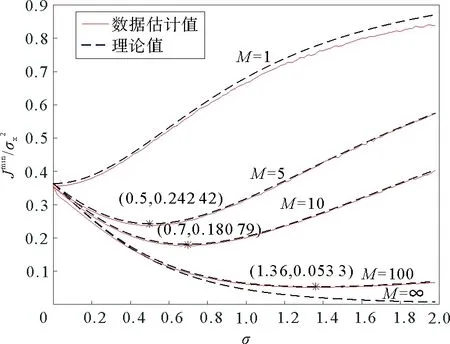
图2 不同节点数目情况下均方误差随着输入噪声强度变化曲线Fig.2 Mean Square Error verus the noise level for different numbers of nodes

利用式(10)～(11)和(18)～(21)进行计算，得出理论和实验的均方误差如图2所示。

图2中，虚线表示理论值，实线表示估计值，横坐标σ=ση/σx，可以清晰地看到，M≠1的情况下在一定噪声强度内MSE随着噪声的增加反而减小，产生了随机共振现象。从图2中还可以看出，本模型在输入信号先验知识未知的情况下，利用数据进行估计的实验结果和理论结果是一致的。图2还给出了不同随机汇池网络的节点数目情况下，均方误差随着加入噪声强度变化的曲线。1个节点下，没有发生随机共振现象。在多个节点下，如图2所示，从5个，10个，100个的均方误差变化情况中，可以发现这3组的均方误差最优值都位于非零噪声强度处，即都出现了随机共振现象。另外，从图2中还可以明显看出均方误差的大小随着节点数目的增加而减小，即节点数目越多，网络的性能越好。依据式(11)，本文还给出了无穷大节点数目(M=)情况下均方误差随着噪声强度的理论变化曲线，实验数据是无法得到的，但是此理论结果告诉我们总可以利用具有充分大的节点数目的随机汇池网络来逼近这一极限。

3 结论

本文建立了一般的自适应加权随机汇池网络模型，理论分析了权系数与噪声两个优化因素下的均方误差性能，得出自适应最优权系数及最小均方误差的表达形式。考虑了信号和噪声统计性未知的情况，实验中利用最小二乘算法验证理论分析。探究了网络节点数目对模型均方误差性能的影响，理论和实验都证明了随着节点数增加均方误差性能能够不断提高。本文只对输入平稳信号的情况下随机汇池网络性能进行了初步研究，对于非平稳随机信号和关于有色噪声对随机汇池网络模型性能的影响等问题值得进一步研究。