高中数学实践活动的有效设计与实施
—— 以“三角比在测量上的应用”为例
2018-02-28徐玉华
◎ 徐玉华
一、活动背景
在实际教学中教师知道,解斜三角形的应用对学生来讲是一个难点,学生在遇到相关的应用题时,往往会遇到以下困难:①不能准确提取相关图形中的关键(有效)信息;②不能将所求问题转化为相应的数学模型;③没有找准合适的方法进行求解。
为了帮助学生更好地克服以上三个方面的障碍,笔者尝试通过开设实践活动课程,从教材中提出的课题入手,整合基础型、研究型及拓展型学习的要素,通过实践、研究、交流、反思来引导学生加强对数学概念(方法)的理解,并尝试将相关概念(方法)运用到实际问题中,不断提高分析问题、解决问题的能力。
二、活动目标
实践活动课的设计从沪教版高一数学教材5.6节中“正弦定理、余弦定理和解斜三角形”的例9引出,提出问题:怎样测量建筑物的高度。实践课的研究围绕这个问题展开,希望能够达成以下三个方面的目标。
(一)知识与技能
(1)学生在实践活动中进一步对三角比和解斜三角形的基本概念及常用方法进行梳理;
(2)学生通过自主设计方案和收集数据,体会如何提取关键信息;
(3)学生通过实践活动逐渐熟悉并开展研究型学习的一般流程。
(二)过程与方法
(1)学生通过实践活动,体会从实际问题到数学建模的转化过程;
(2)学生通过实践活动,进一步感受提出问题、分析问题、解决问题的研究过程。
(三)情感、态度和价值观
(1)通过小组合作,形成良好的互助合作学习的氛围;
(2)通过小组自评、同伴互评等形式,鼓励学生人人都能主动参与学习。
三、活动过程
在完成解斜三角形的相关基础型教学内容后,笔者开展了关于“三角测量”的实践活动课的研究。实践课的设计为3课时,主要包括以下三个板块。
(一)板块一
在完成相关教学内容后,教师提出研究性问题:在已经学习了解斜三角形的有关定理和基本方法后,学生尝试设计有效方案,在学校操场内测量计算东方明珠中球的最高点到东方明珠顶端的距离,并完成实验报告。
1. 学生活动
(1)学生分组,以5—6人为一组,组成研究小组,共同完成实践活动;
(2)实验准备,根据教材提示,设计并制作“量角器”,准备卷尺、纸、笔、计算器等测量及计算工具;
(3)方案设计,小组讨论,结合教学内容,设计测量方案,明确需要测量的数据;
(4)数据收集,根据小组讨论设计的方案,进行实地测量,并记录相关数据;
(5)数据处理,根据测量所得的数据,选择合适的方法对数据进行处理,计算得出东方明珠中球的最高点到东方明珠顶端的距离;
(6)方案修正,小组结合计算结果,对方案设计、数据收集和处理等环节进行反思分析,进一步对方案进行优化或修正,并完成实验报告。
2. 教师活动
(1)对学生的分组情况进行评估(可根据学生的学习能力对个别学生进行微调),指导小组在实践活动中进行明确分工;
(2)在学生活动过程中加强对学生行为的调控,引导学生逐渐熟悉并开展研究性学习的流程与步骤;
(3)对学生提出的设计方案给予及时的点拨,引导学生对收集的数据和计算结果进行理性思考与分析;
(4)指导学生规范完成实验报告。
(二)板块二
各小组在完成相应的实验报告后,安排1课时的时间,组织各小组对实践活动进行汇报交流。
1. 学生活动
(1)小组汇报,各小组派代表介绍本组的研究与思考,并完成小组合作自评表。
下面以某一个小组的交流汇报为例来加以说明。
●实验目标:在学校操场内测量计算东方明珠中球的最高点到东方明珠顶端的距离。
●实验准备:仰角的测量:量角器、线绳。
距离的测量:卷尺。
数据处理:纸、笔、计算器。
●实验方案:在操场B处测得东方明珠中球最高点Q与东方明珠顶端P的两个仰角,前进一段距离到C处,再测得Q、P两处的仰角,收集有关数据,可计算PQ的距离。
上述方案可用如图1所示的数学模型表示。
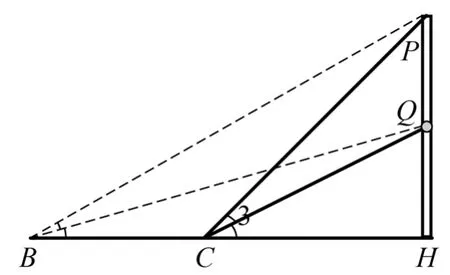
图1 实验方案对应的数学模型
●数据收集:根据上述方案,需要收集的数据有四个仰角∠PBH、∠QBH、∠PCH和∠QCH,以及BC的长度。
●数据处理:在ΔPBC中运用正弦定理,可以求出PC的长,进一步在RTΔPCH中,求出PH的长;同理,在ΔQBC中运用正弦定理,可以求出QC的长,在RTΔQCH中,求出QH的长。由PQ=PH-QH,得到PQ的长。
●实验结论:我们组在实验过程中一共测量了5组数据,根据计算,分别得到如下结果:
第一组PQ=15.2米 第二组PQ=6.95米
第三组PQ=172米 第四组PQ=152米
第五组PQ=145米
查阅有关资料,实际东方明珠中球的最高点到东方明珠顶端的距离约为468–295=173米。
●误差分析:经过小组讨论分析,实验结论与实际距离产生偏差的原因主要有以下几个。
① 读取数学的精确度不够造成误差;
② 读取仰角时视线所在的直线偏移导致仰角的读数误差较大;
③BC之间的距离设定过短;
④ 计算上的误差。
●反思收获:①团结的作用非常大;
② 实验过程中遇到很多困难,但是大家积极动脑,及时修正方案和数据;
③ 思考问题要严谨;
④ 有同学另辟蹊径,解题方法多样化;
如图2所示,有同学提出可利用相似三角形求解。
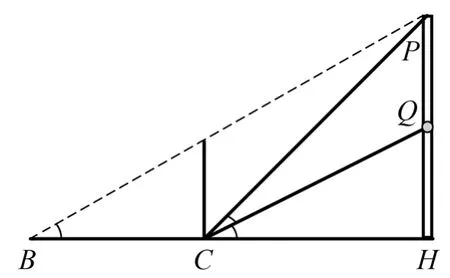
图2 利用相似三角形求解
⑤ 数学来源于生活,应用于生活;
⑥ 差之毫厘,谬以千里。
(2)同伴评价,在小组汇报交流的基础上,其余各组围绕汇报内容给出补充和建议,并根据汇报情况完成评价量表。
例如,有其他小组成员提出,在上述方案的求解过程中,还可以利用如下方法:如图3所示,在RTΔPBH和RTΔPCH中,利用锐角三角比求出PH和CH,进一步在RTΔQCH中,求出QH,PH–QH即为所求距离。

图3 利用锐角三角比求解
2.教师活动
(1)对于小组汇报进行前期的指导;
(2)和学生商议制定实践活动以及小组交流评价量表(见表1)。
(三)板块三
学生完成实践活动课后,安排1课时,组织学生进行拓展研究。
1.学生活动
(1)变式研究,尝试设计方案。用测角仪与皮尺,在上海延安东路外滩测量金茂大厦与东方明珠之间的距离。现将实际问题转化为数学模型,寻找合适的方法求解,如图4所示。

表1 小组合作学习评价表
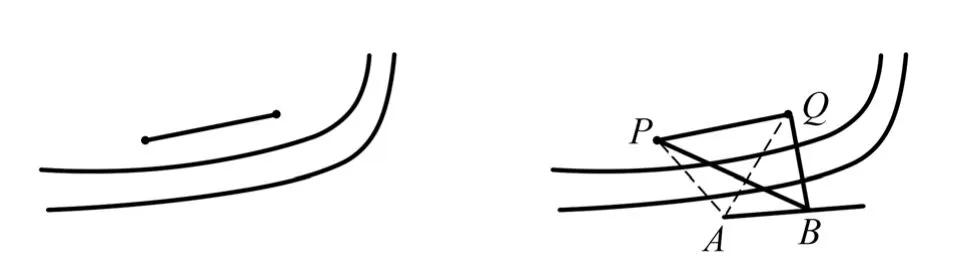
图4 学生活动对应的数学模型
(2)拓展阅读,阅读简易测距的基本方法,探究其蕴含的数学原理。跳眼法为将臂向前伸直,竖起拇指,闭左眼,使右眼的视线沿拇指一侧对准目标左侧(即基准点),头和手保持不动,再闭右眼,使左眼视线通过拇指的同一侧,并记住视线对准的实地某一点,然后目测基准点至该点的宽度,将此宽度乘以10,即为站立点至目标的距离。
跳眼法的基本原理:通过估计跳眼所见实地宽度的方法进行的估略测量。根据两瞳孔的间隔约为自己臂长的1/10,将测得实地物体的宽度乘以10,即为站立点至目标的距离。
跳眼法的数学模型如图5所示。

图5 跳眼法的数学模型
2.教师活动
(1)提供学生拓展阅读材料;
(2)指导学生思考三角比在测量问题中的基本应用,并总结常见模型。
四、活动成效及反思
在开设实践活动课的过程中,笔者欣喜地发现,学生无论是在知识层面还是在能力方面,甚至于在对待数学学习的态度上都有了很大的变化。
(1)大部分学生对于三角比在测量问题中的应用有了清晰的认识,在后续的学习中,能够顺利地将实际问题转化为相应的数学模型,并能准确读取关键信息,对于正弦定理、余弦定理的公式使用也更为熟练。
(2)实践活动以小组形式开展,大家分工合作让每一位学生都有机会参与到活动中来(教师在学生自主分组后会根据学生学习能力的不同进行人员的微调),即便对于一些学力较弱的学生也能获得积极的情感体验,不少学生表示原来学数学还是挺有趣的,对于数学学习的兴趣和投入都有大幅度的提升。
(3)小组交流环节,对于学生表达的逻辑性、规范性和完整性都有一定的要求,设计的现场提问和答辩环节对小组成员思考的缜密性和临场反应也是一种挑战和锻炼。
(4)对于小组活动采用小组自评、同伴互评和教师评价的综合评价方式,能够更加客观地对学生的学习行为进行评估,形成较为完善的评价机制。
(5)在实践活动课中设计拓展阅读的板块,旨在拓宽学生的知识面,引导和鼓励学生能在课外开展自主学习,这个环节也引起学生的兴趣,有部分学生在课后主动收集和学习了三角测距的有关资料,并完成了研究论文《三角测距》。
(6)数学教学不仅是向学生传授知识与技能,更重要的是培养学生对待学习的态度和习惯,当学生在实验报告反馈中意识到“差之毫厘,谬以千里”后,他们不再轻易为自己的粗心找借口,而是以更加审慎的态度对待自己的学习过程,也许这就是教育教学最大的成效所在。
徐玉华 上海市澄衷高级中学 200082
