一类随机不确定网络控制系统的H∞滤波器设计❋
2018-02-28李明扬褚东升于海波
李明扬, 张 玲❋❋, 褚东升, 于海波
(1.中国海洋大学工程学院,山东省高校海洋机电装备与仪器重点实验室, 山东 青岛 266100; 2.中国海洋大学基础教育中心, 山东 青岛 266100)
近年来,网络控制系统(Networked Control System,NCS)已成为控制领域的研究热点之一。NCS通过网络将控制系统的各部分联接起来,实现了分布式的反馈控制。然而,由于网络带宽的限制及信号传输中的干扰因素的存在,在NCS的信道中会出现数据包的丢失、滞后等现象,而且信号可能受到加性或乘性的噪声干扰。
NCS的概念由Walsh[1]首次提出,考虑到NCS中的丢包问题,Sahebsara等通过伯努利变量描述了丢包问题,并建立了带丢包的NCS模型,其中数据包丢失同时发生在传感器-估值器(Sensor to estimator,S-E)通道和控制器-执行器通道(Controller to actuator,C-A),并设计了其H∞和H2滤波器[2-3];孙书利等[4]针对该多丢包模型,设计了线性最小方差意义下的最优滤波器,梁彦等[5]将此成果推广到一般的NCS。同时NCS中的时滞和丢包并发的情形也得到了广泛研究,孙书利等讨论了观测通道中同时带有多步丢包和有限步时滞的模型[6],但该模型中同一数据包需多次发送,可能导致信道拥塞。文献[7]对文献[6]中的模型进行了改进,模型中数据包仅需传输一次,减轻了信道压力,其后此成果被推广到一般的NCS中[8]。但同时考虑多步时滞和丢包的模型较复杂,不便于实际应用,而且数据经多步时滞后的可用性已不大,因此一步时滞和丢包模型正受到越来越多的关注。孙书利[9]提出了带有一步时滞和多丢包的NCS模型并研究了最优滤波算法,李秀英等[10]又对其模型进行了改进,减少了增广维度,并设计了其H∞滤波器。
乘性噪声作为一种重要的信道扰动,在石油地震勘探、卫星姿态估计、水声通信、目标跟踪中已有广泛应用。Gershon[11]和张玲[12]等分别研究了带乘性噪声系统的H∞滤波和最优滤波算法,马静等[13]将乘性噪声引入到含有丢包的NCS模型中来,并推导了相应的最优滤波算法,在一定程度上推广了NCS模型,但此文献并没有考虑NCS中含有随机时滞的情形,而且模型中的乘性噪声只存在于S-E通道中。
本文改进了文献[10]提出的一步时滞和丢包模型,综合考虑了S-E和C-A通道中的丢包、时滞、乘性噪声因素,建立了一类随机不确定网络控制系统的模型。针对此模型,利用线性矩阵不等式方法设计了其H∞滤波器,并对滤波算法进行了仿真验证。
1 系统模型建立
带乘性噪声系统模型如下:
(1)

η1(k-1))η2(k)]y(k-1)} ,
(2)
ζ1(k-1))×ζ2(k)u(k-1)+[1-(1-
(3)
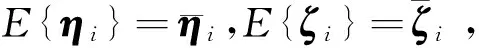
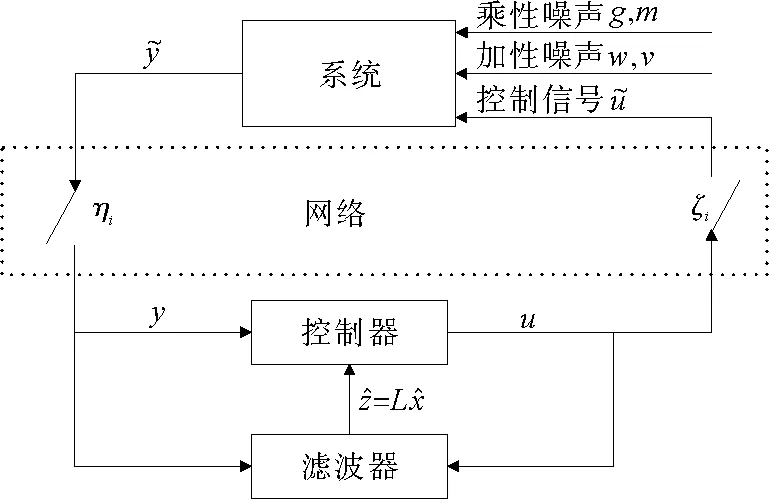
图1 系统结构图Fig.1 NCS schematic
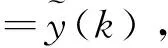
从上述模型出发,定义伯努利变量如下:
(4)

(5)
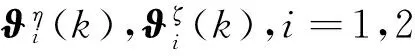
(6)
(7)
(8)
(9)
对系统(1),(2),(3)进行增广,令
φ(k+1)=
得到增广系统:
(10)
其中:z(k)为被估计状态;L为常系数矩阵。随机系数阵满足:



定义如下:

本文设计的H∞滤波器结构如下:
(11)
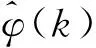

(12)
其中:
并将上述系数的期望标记如下:

2 H∞性能分析
定义1 对误差系统(12),若存在常数δ>0和0<τ<1,使得对∀k>0,当输入u(k)=0,w(k)=0时,E{‖ξ(k)‖2}≤ατkE{‖ξ02},则系统是均方指数稳定的。
定义2 对误差系统(12), 当输入u(k),w(k)∈l2(0,∞)非零时,若存在常数γ>0使滤波误差满足:
ρ‖u(k)‖2},ρ>0
其中,ρ是已知常数,则系统满足给定H∞性能指标γ。
定理1 当误差系统(12)输入为零,即u(k)=0,w(k)=0时,如果存在正定矩阵P,使得
E{AT(k)PA(k)}-P<0 。
(13)
那么该系统是均方指数稳定的。
证明 选取Lyapunov函数V(k)=ξT(k)Pξ(k),则
E{ΔV(k)}=E{V(k+1)|ξ(k)}-E{V(k)}=
ξT(k)E{AT(k)PA(k)-P}ξ(k)。
(14)
假设式(13)成立,则P>0,由文献[2]中命题1可知,系统(12)是均方意义下稳定的。
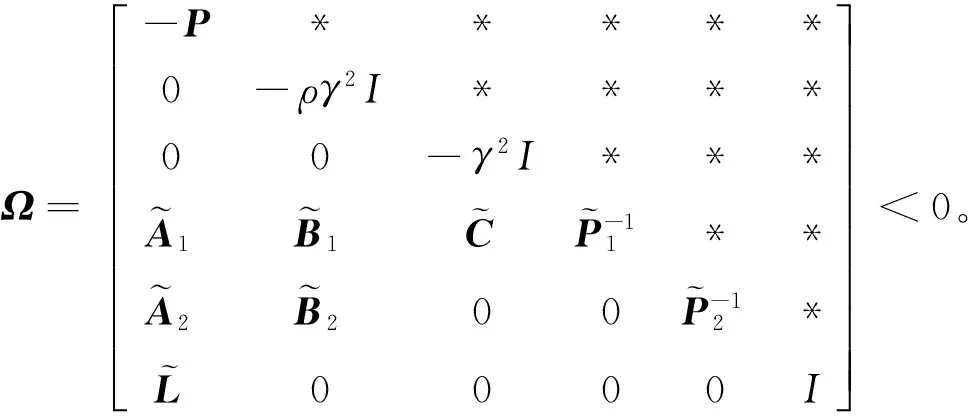
其中:

系数定义为:


证明 由系统(12)可得
(16)
由E{ΔV(k)}=E{V(k+1)|ξ(k)}-E{V(k)},得到
E{ΔV(k)}=βT(k)×
β(k)-ξT(k)Pξ(k) 。
(17)
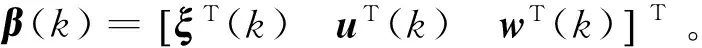
对于任意矩阵Si,Sm,Tj,Tn,有下式成立:
(18)
其中,Sim=Si-Sm,Tnj=Tn-Tj。将系统(12)中各系数定义代入式(17),并考虑式(18),可得式(17)各项为:
将以上各式代入式(17),可得:
E{ΔV(k)}+E{‖e(k)‖2}-
γ2E{‖w(k)‖2+ρ‖u(k)‖2}=βT(k)Ψβ(k),
(19)
其中:
(20)
由Schur补引理[14]可得,式(15)等价于Ψ<0,即式(19)是负定的。因此,当k从0到∞时累加式(19)可得:
(21)
由于零初始条件下E{ΔV0}=0,故可得
ρ‖u(k)‖2} 。
(22)
说明此时系统(12)满足给定的H∞性能指标γ,证毕。
3 H∞滤波器设计

XY+UVT=I,UTV+X2Y2=I,
XV+UY2=0,UTY+X2VT=0。
对式(15)进行合同变换,左右同乘diag{Q,I,I,I,I,I},得到
(23)

(24)
其中
(25)
Π1=diag{-Π,-Π,-Π,-Π,-Π,-Π,-Π};
Π2=diag{-Π,-Π,-Π,-Π};




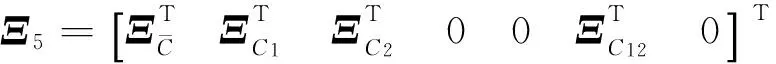


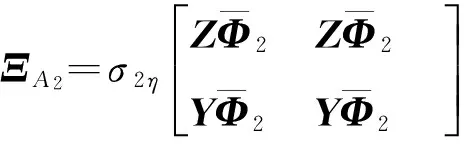




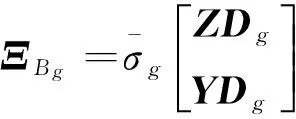

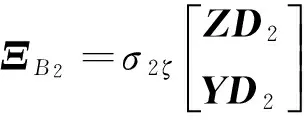

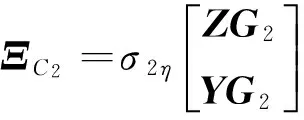

K1=VCf;K2=VAfUTZ;K3=VBf;K4=LfUTZ。
综上可知线性矩阵不等式(25)等价于式(15),故不加证明得给出以下结论:
定理3 系统(1)~(3)的H∞滤波器设计问题可以归纳为:
(26)
不妨取V=VT=-Y,U=UT=Z-1-Y-1,则可以得到滤波器的参数为Af=-Y-1K2(Z-1-Y-1)-1Z-1,Bf=-Y-1K3,Cf=-Y-1K1,Lf=K4(Z-1-Y-1)-1Z-1。
4 仿真
对带乘性噪声系统(1),考虑如下算例:
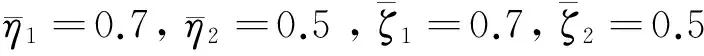
上述其他参数不变,当扰动项w(k)为1/k2时,仿真结果如图4所示。说明当系统中的加性扰动为非高斯噪声信号时,本文的滤波器也能有效地估计系统状态。

图2 真值与滤波值Fig.2 True value and estimation

图3 均方误差对比Fig.3 Comparison of MSE

图4 真值与滤波值Fig.4 Ture value and estimation
5 结语
本文建立了一类带乘性噪声网络控制系统的模型,在模型中综合考虑了传感器-估值器信道和控制器-执行器信道中的乘性噪声、丢包和时滞因素;利用状态增广将信道中的不确定性转化为随机的系统参数,并通过线性矩阵不等式方法设计了随机参数系统的H∞滤波器。与传统的Kalman滤波器相比,本文的滤波器无需已知加性噪声的统计特性,且当加性扰动为非高斯噪声时也能适用。
[1] Gregory C. Walsh, Hong Ye, Linda G. Bushnel. Stability analysis of networked control systems [J]. IEEE Transactions on Control System Technology, 2002, 10(3): 438-446.
[2] Sahebsara M, Tongwen Chen, Shah S L. Optimal H2filtering in networked control systems with multiple packet dropout [J]. IEEE Transactions on Automatic Control, 2007, 52(8): 1508-1513.
[3] Sahebsara M, Tongwen Chen, Shah S L. Optimal H∞ filtering in networked control systems with multiple packet dropouts [J]. Systems & Control Letters, 2008, 57(9): 696-702.
[4] Sun S L, Xie L H, Xiao W D, et al. Optimal linear estimation for systems with multiple packet dropouts [J]. Automatica, 2008, 44(5): 1333-1342.
[5] Liang Y, Chen T W, Pan Q. Optimal linear state estimator with multiple packet dropouts [J]. IEEE Transactions on Automatic Control, 2010, 55(6): 1428-1433.
[6] Sun S L. Linear minimum variance estimators for systems with bounded random measurement delays and packet dropouts [J]. Signal Processing, 2009, 89(7): 1457-1466.
[7] Sun S L. Optimal linear filters for discrete-time systems with randomly delayed and lost measurements with/without time stamps [J]. IEEE Transactions on Automatic Control, 2013, 58(6): 1551-1556.
[8] Sun S L, Ma Jing. Linear estimation for networked control systems with random transmission delays and packet dropouts [J]. Information Sciences, 2014, 269(2): 349-365.
[9] 孙书利. 具有一步随机滞后和多丢包的网络系统的最优线性估计 [J]. 自动化学报, 2012,38(3):349-356. Sun S L. Optimal linear estimators for discrete-time systems with one-step random delays and multiple packet dropouts [J]. Acta Autom. Sin., 2012, 38(3): 349-356.
[10] 李秀英, 王金玉. 具有一步随机时滞和多丢包的网络系统H∞滤波器设计 [J]. 自动化学报, 2014,40(1): 155-160. Li X Y, Wang J Y.H∞Filter Design for Networked Systems with One-step Random Delays and Multiple Packet Dropouts [J]. Acta Autom. Sin., 2014, 40(1): 155-160.
[11] Gershon E, Shaked U, Yaesh I.H∞control and filtering of discrete-time stochastic systems with multiplicative noise [J]. Automatica, 2008, 37(3): 409-417.
[12] Zhang Ling, Zhang Xian-Da. An optimal filtering algorithm for systems with multiplicative/additive noises [J]. IEEE Signal Processing Letters, 2007, 14(7): 469-472.
[13] Ma Jing, Sun S L. Optimal linear estimation for systems with multiplicative noise uncertainties and multiple packet dropouts [J]. IET Signal Processing, 2012, 6(9): 839-848.
[14] 俞立. 鲁棒控制-基于线性矩阵不等式处理方法 [M]. 北京: 清华大学出版社, 2002. Yu Li. Robust Control Based on LMI method [M]. Beijing: Tsinghua University Press, 2002.
