国际原油期货市场无偏预期假说的分位数协整检验

■杨少华，郭万山

一、引言

为满足现货商防范风险和投资者投资需求，期货市场伴随着现货市场的发展应运而生，两者有机的结合完善了现代市场体系，因期货市场特殊的价格引导作用和套期保值功能而成为市场经济体系不可替代的重要组成部分。而原油期货市场的发展速度、方式、规模、参与者数量、衍生品种类更是达到了空前的水平，成熟的原油期货市场由于具有高效的竞争交易机制，往往能将经济基本面的变动迅速地在价格中反映出来，起到市场价格风向标的作用，因此，研究原油期货市场的有效性或原油期货价格是否是现货价格的无偏预期具有重要意义。

Bigman et al.(1983)最早实证检验了期货市场无偏预期假说，基于1975年1月至1980年9月美国小麦和大豆期价和现价数据，他们发现近期期价与交割日现价满足市场无偏预期假说，而远期期价与相应现价不满足无偏预期假说。但Maberly（1985）、Elam&Dixon（1988）对Bigman et al.（1983）的研究提出了异议，因为随机干扰项与自变量可能存在相关性和导致OLS估计失效的数据非平稳性的存在可能对市场有效的原假设做出错误的判断。为了解决实证研究中时间序列的平稳性问题，Hansen&Hodrick（1980）等人将现货价格及期货价格分别进行一阶差分后再进行回归研究。在此之后，协整理论与方法的诞生和成熟为期货市场无偏估计检验提供了新的计量工具。以极大似然法为理论基础，Johansen&Juselius(1990)提出了能对模型参数做出估计的J-J协整检验因其检验期货市场有效性的较好效果成为上世纪90年代检验期货市场有效性的通用方法，如Wang&Ke(2005)利用J-J协整检验方法检测出连豆期价与郑州粮食批发市场的现货价格没有关系、与天津粮食批发市场的现货价格存在协整，郑麦期价与两个市场的现货价都不存在协整关系，参数联合检验显示期货市场不具有有效性。

在原油期货市场效率的检验方面，Coppola(2008)分别选取了纽约商品交易所（NYMEX）不同时期交易的WTI期货和现货价格，使用E-G两步法和J-J协整检验法检验出原油期货价格和现货价格存在长期均衡关系，可用前者预测后者。Salah&Hamid(2004)发现1月和12月原油期货价格对现货价格的预测能起到显著作用，而3、6、9月的期货价格对现货价格的预测效果不佳。在国内学者中，余炜彬等(2004)通过单位根检验和协整关系检验发现Brent原油期货市场在5个月内的期货价格能较为准确地预示未来的现货价格走向，具有价格发现功能，但其有效性随着期货和约期限的拉长而逐渐变小。程刚等(2009)的研究表明，以2004年为分水岭，在2004年之前原油期货市场是有效的，期价对到期日现价基本是无偏预测，但在2004年后原油期货市场是无效的，期价对到期日现价的预测显著有偏。

我们注意到，上述研究所使用的E-G两步法和J-J协整检验法都是在条件均值处讨论变量之间的关系，事实上，由于期货和现货价格数据通常呈现“尖峰厚尾”的分布特征，因此，研究数据分布上其他分位数上的期现价格关系同样十分重要。Xiao(2009)提出的分位数协整模型则很好地解决了该问题，相对于条件均值协整模型，分位数协整模型能更全面地描述条件分布的不同分位数上的动态行为，因此本文应用Xiao(2009)提出的分位数协整模型，研究国际原油期货市场的无偏性假说，更为全面描述期货价格与现货价格之间的关系。相比于以往线性和非线性协整模型，分位数协整模型具有以下几个优点：首先，分位数协整模型允许协整系数值受到每一期革新项的影响，且在不同分位数下是不同的，体现出分位数相依性。该方法也可以看作是随机系数协整模型，而传统的协整模型仅仅是其特例。特别地，不同于以往基于条件均值模型研究期货价格对现货价格的平均影响，分位数协整模型能更全面描述整个条件分布，得到更为丰富的动态行为。其次，分位数协整模型不仅可以研究变量之间在各分位数下是否存在长期均衡关系，还能提供严格的检验程序，检验各分位数下期货市场的无偏性，换句话说，该方法提供一种创新方式来研究无偏性假说的局部有效性，即在哪些分位数下无偏性假说成立，而在哪些分位数下，无偏性假说可能不成立。最后，相比于传统协整方法容易受到异常观测和数据非正态性影响，分位数协整模型更为稳健，因此其所得结果更为可靠。

二、期货市场无偏预期假说的检验方法

Fisher(1986)最早给出了无偏预期检验的“纯粹预期理论”——利率期限结构预期假说，认为短期利率的平均值可用长期利率来预测，可专业的表述为即期利率的无偏估计是远期利率。借鉴Fisher的预期理论，如果期货市场是有效的，则期货价格是未来即期现货价格的无偏预期。Bigman et al.(1983)认为，若期货市场是有效的，则到期日的现货价格与当前期货价格的差为随机游走过程，用数学语言可描述为：

这里Ft，t+n是在t+n时到期的期货合约在时期t的价格，st+n为时期t+n时的现货价格，Φt是时期t的信息集，Et为时期t时的信息集下的条件期望。上式意味着：在给定的t时信息集下，t+n时到期的期货合约在t时的价格是t+n时现货价格st+n的无偏估计。随着市场的变化和价格的波动，新产生的信息不断增加到原信息集中，这样，某时刻的信息集就包含之前所有时刻的信息集，也就是说对于所有的时刻t，当τ≥0时，有Φt+τ⊇ Φt。考虑到期日为T在时刻t和t+τ的期货价格Ft，T和Ft+τ，T（t≤T，T+τ≤T），若期货市场有效，则有：

且Φt+τ⊇ Φt，因为 t≤t+τ，所以 Ft+τ，T比Ft，T包含了更多的信息，对现货市场价格的预测更为准确。期货市场无偏性假说的检验通常是在协整理论框架下进行，其计量方程如下：

其中ut为随机误差项，α和β为待估参数。期货市场有效的原假设是：α=0且β=1。

需要指出的是，无偏预期假说是在假定市场参与者是风险中性的情况下进行的检验过程，这种假设与期货市场中的实际情况不符，比如：生产者为了规避未来可能的市场风险，利用期货合约对产品套期保值，由此产生的风险溢价使期价偏离未来现价的预期值。因此，对期货市场有效性的检验应考虑风险溢价的存在（Fama&French，1987）。如果考虑市场风险溢价的存在，则式（3）中的α不必为零。因此，在风险溢价存在情况下，对期货市场无偏预期假说的检验只要检验β=1的原假设即可，本文在实证过程中也将只对β=1的原假设进行检验。

三、分位数协整模型

（一 ）线性条件均值协整模型

在对式（3）进行OLS估计时，如果序列是非平稳的，则可能导致“伪回归”。Engle&Granger(1987)提出单方程线性协整模型较好地解决了这一问题，其形式如下：

其中，yt和xt分别为1维和p维的I(1)序列，ut为平稳的I(0)变量。协整检验分为两个步骤：首先采用OLS方法估计式（4）中的参数；然后对估计残差进行单位根检验，如果残差平稳，则说明变量之间存在稳定的协整关系。由于xt与ut的相关性，对式（4）采用OLS法进行估计时，会导致估计的二阶偏差，Saikkonen(1993)、Stock&Watson(2009)建议将式（4）中的ut分解为领先、滞后项πj和纯革新项et，则式（4）可以转化为如下形式：

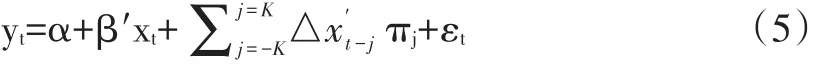
从而xt与εt不具有相关性，达到消除OLS估计二阶偏差的目的。在实践应用中，我们不仅仅要得到参数估计值，而且想知道参数与某些已知值是否相等，考虑如下的线性约束问题：

其中R为q×p型矩阵，r为q维向量。Hamilton(1994)对于式（6）的假设检验问题，给出了如下wald形式的检验统计量：

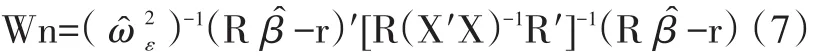
（二 ）分位数协整检验

传统线性协整模型仅反映出因变量对自变量的平均响应，由于条件均值只是概率分布的一个特征，利用线性条件均值协整模型无法了解分布的其他分位数上自变量和因变量的长期均衡关系，若要了解分布上其他分位点上的变量间的关系应对上述方法进行改进，基于此，Xiao应用Koenker&Bassett(1978)的分位数回归方法提出的分位数协整模型（Quantile Cointegration Model）很好地解决了上述诉求。记εt的τ分位数为Qe（t），It=σ{xt，△xt-j，∀j}，则对于式（5）中yt的条件τ分位数为：

其中，Fε（·）为εt的累积分布函数。令α（τ）=α+（τ），（1，x，△x′t-K，…，△x′t+K，）′，和θ（τ）=（α（τ），β（τ）′，π′（Kτ），…，π′-（Kτ））′，则式（8）可以表示为如下形式：

在上述模型中，协整系数受到每一期革新项的影响，在不同分位数下是不同的，体现出分位数相依性，Xiao（2009）称为分位数协整模型，可以描述在不同分位数处变量间的长期均衡关系，得到更为丰富的动态行为。

对于式（9）中θ（τ）的估计，需要解决以下问题：

此处，ρτ（u）=u（τ-I（u＜0）），其中I（u＜0）为示性函数，当{u＜1}时取1，否则取0。利用微分方法求解式（10）比较困难，可借助线性规划的办法来求解，Koenker&Bassett(1978)对上述问题求解过程有详细介绍。

分位数协整模型关心的是在分位数τ下变量之间是否具有协整关系，Xiao(2009)基于累加和残差（cumsum residual）给出如下的检验统计量：

其中，εtτ=yt-Qyt（τ│It），ψτ（u）=τ-I（u＜0），为ψτ（εtτ）长期方差的一致非参数估计量：

为得到检验统计量CS（τ）的临界值，考虑如下部分和过程：

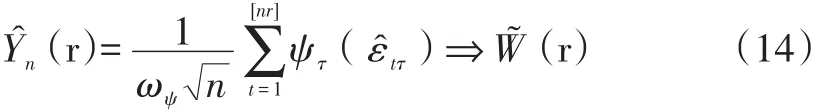
其中

W1和W2为独立的1维和p维标准布朗运动。若原假设成立且在τ分位数下具有协整关系，则

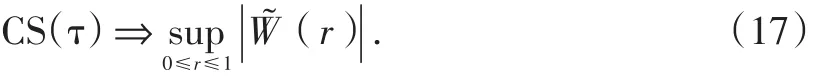
因此，分位数τ下的协整关系检验统计量的渐近分布与Xiao&Phillips(2002)在线性条件均值协整模型给出的检验统计量的渐进分布相同，其模拟临界值参见Xiao&Phillips（2002）。基于分位数协整模型，考虑在分位数下形如式（6）的经典协整系数的线性约束检验问题：

针对上述假设检验问题，Xiao(2009)给出如下的分位数Wald检验统计量：

在分位数协整模型中，另一个重要的统计推断问题是各分位数下的协整系数是否相等，如果各分位数下的协整系数相等，则分位数协整模型可转化为线性协整模型。基于此，Xiao(2009)提出如下假设检验问题：

其中，β为未知的常数向量，Xiao(2009)建议使用线性协整模型的OLS估计β代替。令Vˆn（τ）=n（βˆ（τ）- βˆ），对于上述检验问题，Xiao(2009)提出如下的Kolmogoroff-Smirnoff检验统计量：

在实证中，令ε∈（0，0.5），在分位数区间Г=[ε，1-ε]中选取n个分位数点（ε=τ1＜L＜τn=1-ε），然后计算每个分位点上的Vˆn（τ）绝对值，最后再取最大值。

由于检验统计量sup ||Vˆn（τ）的大样本分布为非标准分布，且受冗余参数的影响，不利于统计推断。因此，Xiao（2009）利用bootstrap方法进行改进，得到了检验统计量sup ||Vˆn（τ）的小样本分布，步骤如下：

1.用普通最小二乘法对式（4）进行估计，得到估计值 αˆ，βˆ和残差 uˆt=yt- αˆ- βˆ′xt；

2.令wˆt=（△xt，uˆt），对wˆt运用向量自回归进行估计：

3.从中心化残差

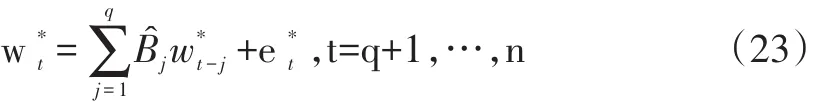
6.重复（2）到（5）多次，得到sup ||Vˆ*n（τ）的经验分布，以此作为sup||Vn（τ）在原假设成立下的近似分布，进行统计推断。

四、实证分析

（一 ）数据及其描述统计

在实证分析中，本文选取国际原油市场比较有代表性的WTI原油现货价格与1月、2月、3月和4月期的期货价格的月度数据为研究对象，对期货价格和现货价格时间序列取自然对数消除可能存在的异方差，分别用lnS、lnF(1)、lnF(2)、lnF(3)和lnF(4)表示，数据来源于国际能源信息署（Energy information administration，EIA），所使用的样本数据的时间跨度为1986年1月到2017年5月，共377个观测数据。在构建月度期货价格序列时，通常存在的问题是相应合约在某个给定日并无交易，因此我们遵循Alquist&Kilian(2010)的方法，将该月度最后一个交易日的相应期货价格作为其月度值①限于篇幅，描述性统计量、单位根检验结果和相关关系矩阵未给出，留存备索。。

现货价格与期货价格的各种描述性统计量极为相似，现货价格和4种合约期的期货价格的偏度均为正值，意味着分布均右偏，而其峰度分别为1.9422、1.9644、1.9665、1.9814和 2.0020，意味着相较于正态分布，峰度较低；Jarque-Bera统计量拒绝现货价格与期货价格的正态分布假设；由于序列的单整是具有协整关系的前提，现货价格与期货价格均为非平稳过程，为下面进行协整分析提供了前提条件；对于相关系数，现货价格与1、2、3和4月的期货价格的相关系数分别为0.9888、0.9748、0.9620和0.9492，随着交割月的增加，其相关性逐渐减小，但仍高于0.94，体现出较强的相关性。

（二 ）E-G两步法协整检验

遵循Xiao(2009)的方法，为检验原油期货市场的无偏性假说，我们构建如下的模型：

经由单位根检验结果得知，现货价格lnS与期货价格 lnF(1)、lnF(2)、lnF(3)和 lnF(4)均为 I（1）序列，为进一步探讨期货价格与现货价格是否存在长期稳定的均衡关系，故需进行协整检验。在此，我们采用E-G两步法，第一步运用OLS法对式（25）进行估计，得到拟合残差；第二步，对拟合残差进行单位根检验，如果残差平稳，则具有协整关系，否则不具有协整关系。因为无偏性假说成立的前提条件是现货价格与期货价格具有协整关系，如果运用E-G两步法，得到现货与期货不具有协整关系，则无偏性假说不成立；若现货价格与期货价格具有协整关系则需进一步检验式（4）中的β=1是否成立，检验统计量为式（7）。对于式（25）中领先与滞后阶数K的确定，我们采用Kejriwal和Perron(2008)的建议，使用BIC信息准则进行选择，结果见表1。

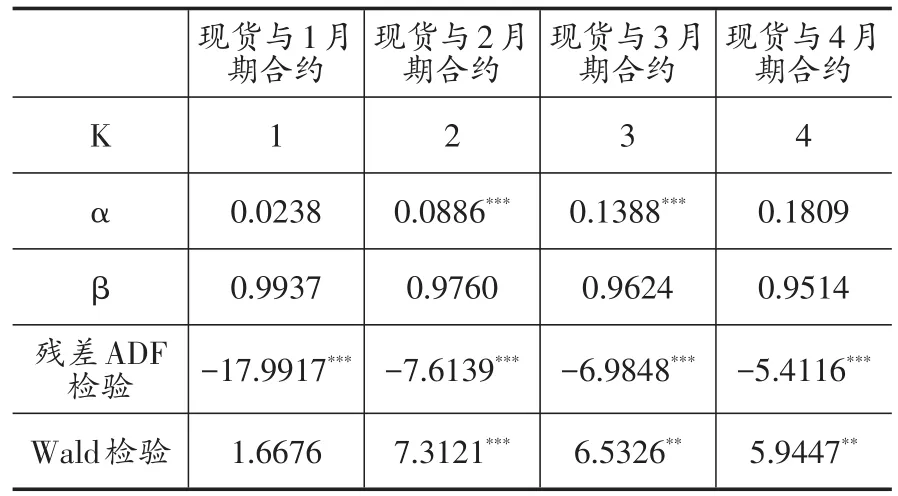
表1 现货与期货的E-G协整检验结果

由表1可以看出，使用BIC信息准则，得到现货与1月、2月、3月和4月期货合约下的领先、滞后阶数K 分别为 1、2、3和 4，β的估计值分别为 0.9937、0.9760、0.9624和0.9514，均非常接近1；残差ADF检验结果显示，现货分别与4个期货合约均具有协整关系。由于协整关系仅是无偏性假说成立的一个必要条件，我们还需要进一步检验β=1是否成立；Wald检验检验结果显示，现货与1月期合约下，β=1成立，而其他几个合约下β=1均不成立，这一点与Bopp&Lady(1987)、Salah&Hamid(2004)的研究结论是一致的，说明原油期货市场在短期是有效的，但在长期是非有效的。该结果的稳健性可通过分位数协整方法对各个分位点上的市场效率的研究进一步验证。

（三 ）分位数协整分析

由于传统的E-G协整模型只能分析平均水平下现货价格与期货价格的长期均衡关系，无法探讨平均价格水平以外的均衡情况。而Xiao(2009)给出的分位数协整模型可借助被解释变量的条件分布分析不同价格水平下的现货价格与期货价格的均衡关系，很好地解决了传统的E-G协整模型不能解决的问题。表2给出各个分位点下WTI现货与相应期货合约的分位数协整模型的参数估计以及各分位数下基于累加和残差的稳健协整检验的结果。

从表2中可以发现，对于现货与1月期合约，β的估计值区间为[1.0179,0.9387]；对于现货与2月期合约，β的估计值区间为[1.0264,0.8993]；对于现货与3月期合约，β的估计值区间为[1.0204,0.8750]；对于现货与4月期合约，β的估计值区间为[1.0414,0.8839]；现货与各期货合约的β估计均值分别为0.9879、0.9706、0.9596和0.9534。由此可见，对于不同的期货合约，β的估计值都非常接近于1。

进一步，我们通过各分位数下的协整检验统计量CS(τ)，判断各分位数下现货与期货是否具有协整关系：对于现货与1月期合约，CS(τ)区间为[0.6136,0.9890]；对 于 现 货 与 2 月 期 合 约 ，CS(τ)区 间 为[0.6725,0.9615]；对于现货与3月期合约，CS(τ)区间为[0.7837,0.9872]；对于现货与4月期合约，CS(τ)区间为[0.6883,0.9222]，均低于10%显著性水平下的临界值1.616。因此在各分位数下，现货与不同时期的期货合约之间存在分位数协整关系，这一点与EG协整检验的结论是一致的。

从表2结果看出不同分位点上β的估计值存在明显的差异，通过做出分位点及β估计值的折线图，并给出b估计值的95%置信区间，可直观看出两者间的关系。如图1所示，横轴为分位点，纵轴为b估计值，可以看出：第一，不同期货合约的不同分位点上b存在明显差异；第二，随着分位数的增大，不同期货合约下，b有变小的趋势，由此说明，随着原油期货价格的上涨，期货价格对现货价格的引导作用在不断下降。

表2 分位数协整估计与稳健协整检验结果

通过分位数协整检验，我们得到各期货合约与现货在各分位数下均具有协整关系。进一步，我们通过分位数协整模型，检验在各分位数下的无偏性假说，即在各分位数下检验β=1的原假设，该过程分为两步：首先，利用sup||Vn（t）检验各分位数下协整系数是否相同，如果协整系数相同，则通过线性条件均值协整模型检验无偏预期假说；其次，如果各分位数下协整系数不同，进一步通过分位数Wald检验，检验各分位数下的无偏预期假说。协整常系数检验统计量sup||Vn（t）由于受到数据非平稳性及多余参数的影响而不具有标准分布，因此我们对现货与四个期货合约分别利用bootstrap方法，重复抽样3000次，可得到分位数上协整常系数检验统计量的临界值，结果如表3所示。

图1 现货与期货的分位数协整关系图

表3 分位数协整常系数检验

基于sup||Vn（t）的协整常系数检验发现，现货与各期货合约之间在各分位数下的协整系数并不相同。因此，下一步，我们需要使用分位数Wald检验来检验各分位数下β=1的原假设是否成立，结果检验见表4。

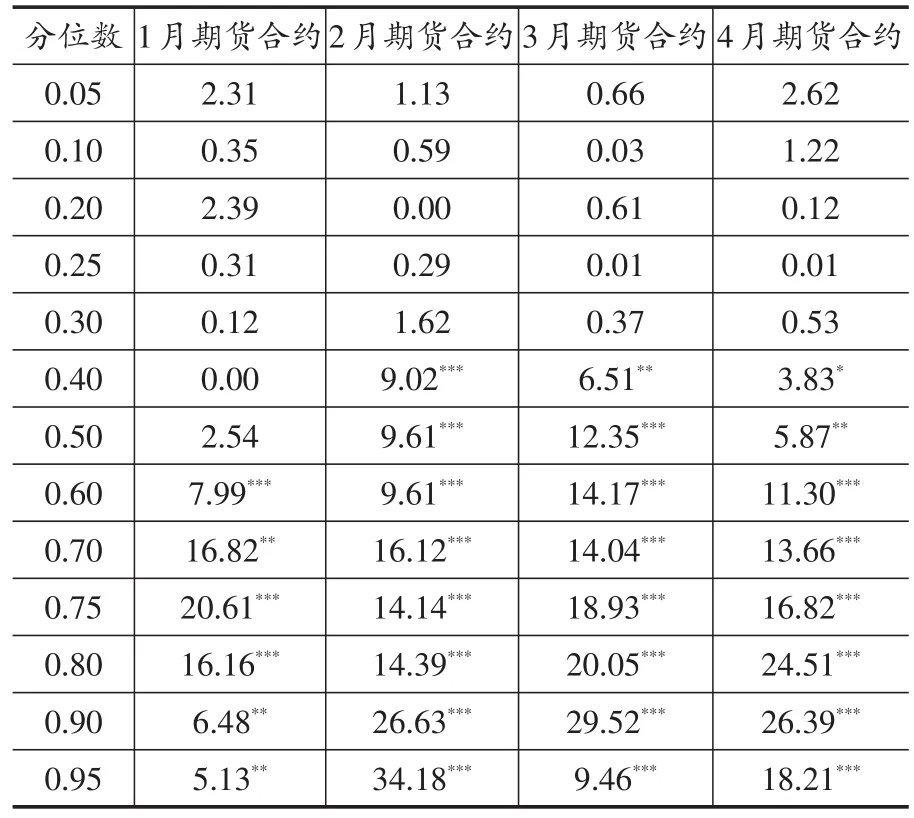
表4 市场效率[β（τ）=1]的wald检验统计量

从表4中可以看出，1月期货合约在0.5以下的分位数上不能拒绝β=1的原假设，2月、3月和4月期货合约在0.3以下的分位数上不能拒绝β=1的原假设。因此，原油期货市场的无偏预期假说并不是在数据分布的所有分位点上都是成立的，对上述四个不同期货合约，期货市场的无偏预期假说仅仅在较低分位数上是成立的，具体来说，1月期货合约在0.5以下的分位数上满足无偏预期假说，而2月、3月和4月期货合约只有在0.3以下的分位数上才满足无偏预期假说。换句话说，只有当期货价格较低时，期货市场才满足无偏预期假说，期货市场才是有效的；而当期货价格走高时，期货市场并不满足无偏预期假说。由此说明，当期货价格受投机因素和外生冲击的影响而走高时，期货市场的无偏预期假说不成立，市场也不再是有效的，期货市场的价格发现功能也就相应会减弱。

五、结论与政策建议

国际原油期货市场经过几十年的发展，已成为世界石油市场价格波动的重要引导因素，对原油期货市场有效性的研究可帮助我们判断通过原油期货价格能否有效预测原油现货价格。本文基于1986年1月到2017年5月的WTI原油现货价格与1月、2月、3月和4月期的期货价格，研究国际原油期货市场上的无偏预期假说是否成立，与传统的基于线性条件均值的协整检验模型不同的是，本文使用分位数协整检验方法来检验无偏预期假说。相比传统协整模型，分位数协整模型对误差项的分布不做任何假设，因此其结果更为稳健、可靠。更为重要的是，该方法可以分析不同分位数下的无偏性假说，从而对两变量之间长期均衡关系提供更全面的描述。本文的实证研究结果显示：所研究的四个期货合约价格与现货价格在所有分位点上均存在协整关系，但是随着期货价格的上升，期货价格对现货价格的可预测性在逐渐减弱。期货价格与现货价格的协整关系存在并不表明国际原油期货市场就一定满足无偏预期假说，基于分位数wald检验的检验结果表明，1月期货合约在0.5以下的分位数上满足无偏预期假说，而2月、3月和4月期货合约只有在0.3以下的分位数上才满足无偏预期假说；也就是说，只有当期货价格较低时，期货市场才满足无偏预期假说，期货市场才是有效的。

本文的研究结果对于投资者而言具有重要意义，在原油价格波动剧烈的今天，国际原油期货市场的价格发现功能在不断减弱，尤其是在原油期货价格走高时，投机成分不断增加，期货价格对现货价格的引导作用减弱，投资者应当注意到其中蕴含的风险，谨慎地在现货市场上进行交易操作。对于中国这样一个石油进口大国而言本文的研究结果具有更重要的意义，自上个世纪九十年代中国成为石油净进口国以来，每年的进口数量在逐步增加，2016年成为第一大石油进口国，全年进口原油3.76亿吨，对外依存度达到65%①资料来源：http://finance.sina.com.cn/chanjing/cyxw/2017-01-13/doc-ifxzqnip0959975.shtml。，对国际原油市场的依赖越来越深，但对国际石油定价的影响却微乎其微，因此，国际原油价格的波动势必对我国经济的发展带来不利影响，增加经济发展成本。因此，为保障能源安全，防范国际原油价格波动对我国经济发展造成冲击，我们应做好以下几方面：第一，充分研究国际期货市场原油价格运行的规律，积极参与国际原油期货交易，规避价格波动带来的风险。第二，掌握国际原油期货市场的价格对国际原油现货价格的预测规律，达到影响国际石油价格的目的，改变我国被动接受国际石油价格的现状。第三，加快建立并完善我国石油期货市场，逐步丰富我国石油期货市场交易品种，争取在国际石油定价体系中起到更大的作用。第四，综合考虑国内石油需求和国际油价实际情况，灵活调整国际原油进口量和国内石油开采量，当国际油价较低时加大国外石油的进口量限制国内石油的开采，拓宽进口渠道，做好石油储备。当国际油价较高时减少国外石油的进口量增加国内石油的开采和供给，最大限度地避免高油价对国内经济的冲击。第五，加大产业结构调整，转变经济增长方式，引导高能耗、低产值的传统资源密集型产业向低能耗、高附加值、高技术含量的方向发展，提高石油的利用率，节约能源。第六，积极发展风能、地热能、太阳能、核聚变能和生物质能等新能源，缓解、消除当前严重的污染问题，降低对石油能源的依赖。

[1]程刚，张珣，汪寿阳.原油期货价格对现货价格的预测准确性分析[J].系统工程理论与实践，2009，29（8）：11～18.

[2]余炜彬，范英，魏一鸣，焦建玲.Brent原油期货市场的协整性分析[J].数理统计与管理，2004，23（5）：26～32.

[3]Alquist R,Kilian L.What do we learn from the priceofcrudeoilfutures?[J].JournalofApplied Econometrics,2010，25（4）：539～573.

[4]AndrewsD W K.Heteroskedasticityand Autocorrelation Consistent Covariance Matrix Estimation[J].Cowles Foundation Discussion Papers,1990,59（3）：817～858.

[5]Bigman,D,Goldfarb D.&Schechtman,E.Futures Markets Efficiency and the Time Content of the Information Sets [J].The JournalofFutures Markets，1983，3（3）：321～334.

[6]Coppola A.Forecasting Oil Price Movements:Exploiting the Information in the Futures Market[J].Journal of Futures Markets,2008,28(1):34～56.

[7]Elam E,Dixon L B.Examining the Validity of a Test of Futures Market Efficiency[J].Journal of Futures Markets,1988,8(3):365～372.

[8]Engle R F,Granger C W J.Co-integration and ErrorCorrection:Representation,Estimation,and Testing[J].Econometrica,1987,55(2):251～276.

[9]Fama E F,French,K.R.Commodity Futures Prices:Some Evidence on Forecast Power,Premiums,and the Theory of Storage[J].Journal of Business,1987,60(1):55～73.

[10]Fisher I. Appreciation and Interest[J].Publications of the American Economic Association,2013,11(4):1～98.

[11]Hamilton J D.Time Series Analysis[M].Princeton University Press,Princeton,1994.

[12]Hansen L P,Hodriek R J.Forward Rates as Optimal Predictors of Future Spot Rates: An Econometric Analysis [J]. Journal of Political Economy,1980,88(5):829～853.

[13]Johansen,S,Juselius K.Maximum likelihood Estimation and inference on Cointegration:With Applications to the Demand for Money[J].Oxford Bulletin of Economics and Statistics，1990，52（2）：169～210.

[14]Kejriwal M,Perron,P.Data Dependent Rules for Selection of the Number of Leads and Lags in the Dynamic OLS Cointegrating Regression[J].Econometric Theory,2008,24(5):1425～1441.

[15]Koenker R,G Bassett,Regression Quantiles[J].Econometrica,1978,46(1),33～50.

[16]Maberly E D.Testing Futures Market Efficiency:A Restatelnent[J].The Journal of Futures Markets,1985,5(3):425～432.

[17]Saikkonen P. Asymptotically Efficient Estimation of Cointegration Regressions[J].Econometric Theory,1991,7(1):1～21.

[18]Salah A,Hamid B.On the Predictive Accuracy of Crude Oil Futures Prices[J].Energy Policy,2004,32(12):1389～1393.

[19]Stock J H,Watson M W.A Procedure for Predicting Recessions with Leading Indicators:Econometric Issues and Recent Experience[J].Nber Chapters,1993:95～156.

[20]Wang H H,Ke B.Efficiencytestsof agricultural commodity futures markets in China[J].Australian Journal of Agricultural & Resource Economics,2005,49(2):125～141.

[21]Xiao Z,Phillips P C B.A CUSUM test for cointegration using regression residuals[J].Journal of Econometrics,2002,108(1):43～61.

[22]Xiao Z.Quantile cointegrating regression[J].Journal of Econometrics,2009,150(2):248～260.