基于复杂网络的危险品道路运输网络优化策略研究

，

(1.云南省交通科学研究院有限公司 交通运输安全研究中心,昆明 650011; 2.中国电建集团昆明勘测设计研究院有限公司,昆明 650051)

0 引言

随着中国能源化工业的迅速发展，危险品运输已成为重要的国民经济活动。相比普通货物运输，危险品运输对象一般具有易燃、易爆、强烈腐蚀性和放射性等，如汽油、炸药、强酸和过氧化物等[1]，因此在运输过程中一旦发生事故，将对环境、周围居民和经济活动的正常运转造成严重的损害。当危险品运输车辆在运输过程中遭遇随机攻击(如交通事故)或蓄意攻击(如恐怖袭击)，运输网络功能将会受损。特别地，当事故发生地点为网络最为“脆弱”的节点或边，则可能导致网络“瘫痪”[2-3]。因此，研究危险品道路运输网络拓扑特性及优化策略有助于提升网络在突发事件下的连通性和抗毁性，复杂网络理论目前是处理这一类问题的有效方法。

欧拉在1736年对格尼斯堡“七桥问题”的研究揭开了复杂网络理论研究的序章，此后人们从网络拓扑角度将众多复杂系统抽象为网络加以描述和研究，如计算机网络、社交网络、电力网络、神经网络和交通运输网络等[4]。1967年Milgram在分析网络结构时首次提出网络的小世界现象[5]，基于此，1998年Watts等人在研究小世界现象生成机制过程中提出WS小世界网络，并首次给出了网络生成算法[6]。1999年Barabási等发现了现实世界网络的无尺度特性，称为BA模型，并给出网络的生成算法[7]。Watts和Barabási等的研究成果颠覆了人们对传统网络的认识，引起物理学、经济学和计算机通信等领域学者对复杂网络的关注[8-10]。现有研究中，国内外学者主要通过图论和网络拓扑等展开对交通运输网络拓扑特性的研究，这种理论方法可以很好地刻画结构较为简单的网络，但对于复杂的运输网络则难以胜任[11]。在应用复杂网络理论研究交通运输网络拓扑特性的成果中，主要集中于铁路网络[12-17]、航空网络[18-23]和城市交通网络[24-27]等。

在关于铁路网络的拓扑特性研究中，学者们首先给出了铁路运输网络的P空间、R空间和L空间3个空间的网络定义[12]。Kurant等[13]对欧洲和瑞士铁路网络的P空间、R空间和L空间3种空间形态进行实证研究，并分析比较了不同空间形态下铁路网络拓扑特性的异同。在P空间形态中，Sen等[14]对印度的铁路运输网络研究表明其具有较短的平均路径长度和较大的聚集系数，呈现出小世界网络特征。赵伟等[15]研究了中国铁路客运网络，研究结果表明铁路的物理网络为树状结构，车流网络是典型的小世界网络。谭江峡[16]和王伟[17]等的研究也得出类似结论。

在关于航空网络的拓扑特性研究中，Guimera等[18-19]对全球航空网络进行研究，结果表明航空网络是小世界网络，平均最短路径为4.4，网络平均聚集系数为0.62。Chi等[20]构建了赋权有向的美国航空网络，研究结果与Guimera等的类似，即美国航空网络也具有小世界特性，平均最短路径为2.4，网络平均聚集系数为0.618。其他学者也进行了类似研究，例如Guida等[21]研究了意大利航空网络，Bagler等[22]研究了印度航空网络，Cai等[23]研究了中国航空网络。他们的研究结果均表明航空网络是小世界网络，且网络平均聚集系数相近，不同的是全球航空网络的平均最短路径大于各个国家的航空网络。

在关于城市交通网络的拓扑特性研究中，Jiang等[24]研究了城市道路网络，表明其具有小世界网络特性。周敏等[25]研究了长株潭城市群的快递服务网络，研究结果表明网络具有一定的小世界特性，其度分布的幂律分布表明网络还具有一定的无标度网络特性。郑啸等[26]通过构建基于邻接站点的有向加权复杂网络模型，研究了北京市的公交网络，结果表明北京市公交网络具有无标度和小世界网络特点。胡一竑等[27]利用GIS技术研究了中国4座城市街道网络的复杂性，研究结果表明4座城市的性质非常相似。

总的来讲，目前关于复杂网络模型及相关实证分析研究已经取得大量成果，但与交通运输网络相关的研究并不多，且主要集中于铁路网络、公交网络、航空网络、轨道交通网络和城市道路交通网络等，鲜有学者将复杂网络理论应用于危险品道路运输网络的拓扑特性及优化策略研究。相对其他运输网络，危险品道路运输网络是一种特殊的交通网络，主要体现在以下几点：1)网络规划理念不同。危险品道路运输网络的规划往往以运输风险最小为基本原则，这也导致危险品运输网络有别于其他道路运输网络；2)网络系统组成要素不同。危险品道路运输网络的路段和节点一般远离路网密度较高的区域，如人口聚集区、学校、水源、桥梁、和政府机构等，这导致其网络形态结构不同于其他运输网络；3)网络规模不同。危险品道路运输网络的节点和边由城市的主干路段和交叉口组成，它是城市道路网络的一部分，但又不同于城市道路网络。考虑上述几点因素，危险品道路运输网络必然呈现与其他运输网络不同的网络拓扑特性，且网络优化策略也不尽相同，因此有必要将复杂网络理论应用于危险品道路运输网络拓扑特性的探究中。

基于上述分析，在充分借鉴现有研究成果的基础上，构建危险品道路运输网络拓扑特性研究流程和方法，以大连市危险品道路运输网络为研究对象，通过统计分析网络平均节点的度、度分布、特征路径长度和网络平均聚集系数等静态统计指标，探索危险品道路运输网络的拓扑特性及相应优化策略，以期为危险品道路运输网络的产生机理和灾害预防提供理论支撑。

1 危险品道路运输网络拓扑特性研究方法

为得到网络的拓扑特性，危险品道路运输网络拓扑特性研究方法主要解决以下几个问题：1)根据哪些因素判断网络拓扑特性；2)如何判断一个网络的复杂网络类型；3)如何构建基于复杂网络理论的危险品道路运输复杂网络模型；4)研究网络拓扑特性的流程。针对上述问题，本文主要通过以下几个方面展开研究。

1.1 复杂网络模型相关理论

1.1.1 复杂网络特征值

1.1.1.1 网络平均节点的度及分布

定义1节点的度 节点的度是指网络中连接某个节点vi的边的数目ki。

为降低在统计网络节点度过程中的起伏和涨落，一般采用度分布函数和累积分布函数来描述网络节点的度分布情况。

定义2度分布函数 度分布函数p(k)是指随机选择某节点vi的度恰好为k的概率。

定义3网络平均节点的度 网络中所有节点的平均度称为网络平均节点的度。计算公式如式(1)所示：

(1)

式中，〈k〉为网络平均节点的度，N为网络节点数目。

对于危险品运输网络上任意交叉口vi，其节点的度D(vi)反映了与交叉口vi直接相连路段的数量。D(vi)越大，则该交叉口的连通性越强。

1.1.1.2 特征路径长度

定义4最短路径距离 在复杂网络中，任意两个节点vi和vj之间，将连接它们距离最短的一条路径的长度dvi,vj称为最短路径距离。

定义5网络直径 网络中所有最短路径集合中最大的一个或几个的数值称为网络的直径T，即T=max{dvi,vj|vi,vj∈V}。

定义6特征路径长度 网络中所有节点对之间的最短路径距离的平均值称为特征路径长度。计算公式如式(2)所示：

(2)

式中，L为网络特征路径长度，N为网络节点数目，dvi,vj为节点vi到vj之间的最短距离。

1.1.1.3 网络平均聚集系数

定义7聚集系数 节点vi和ki个节点相连，这ki个节点之间互相连接的边数为Evi，则这Evi个边与ki个节点之间可能存在边的数目之比称为聚集系数。计算公式如式(3)所示：

(3)

式中，Cvi为节点vi的网络聚集系数，kvi为节点vi的相邻节点数目，Evi为节点vi的相邻kvi个节点之间互相相连边的数目。

定义8网络平均聚集系数 网络中所有节点的网络聚集系数平均值。计算公式如式(4)所示：

(4)

式中，C为网络平均聚集系数，N为网络节点数目。

网络平均聚集系数反映了网络中某个节点与其相邻节点之间的连接程度，表示网络的局部化特征。

1.1.2 复杂网络类型

对复杂网络进行类型划分是应用复杂网络理论实证研究危险品道路运输网络拓扑特性的首要条件。按网络拓扑结构特征来划分，目前复杂网络主要分为随机网络、小世界网络和无标度网络3种[28]，拓扑特性具体如下。

1)随机网络

若某网络节点的度分布p(k)可表示为p(k)=e-αk，即节点的度分布服从指数分布，则认为该网络新增节点与已存在节点之间的连接随机连接，这种网络称为随机网络[7]。现有研究结果表明，随机网络通常具有较小的特征路径长度，但无明显的聚集特性。

2)小世界网络

若某网络的拓扑统计特性表现为较大的网络平均聚集系数和较小的特征路径长度，则这种网络称为小世界网络[6]。通常可表示为：

L≥LR

(5)

CCR

(6)

式中，LR为随机网络的特征路径长度，CR为随机网络的网络平均聚集系数，该随机网络与研究网络的节点和边数相同。LR和CR分别是lnn/lnk和k/n的等阶量，一般将上述等阶视为等量关系处理，而不影响判断结果，故有如下关系：

LR=lnn/lnk

(7)

CR=k/n

(8)

3)无标度网络

若某网络节点的度p(k)可表示为p(k)=k-β的幂律函数形式，则这种网络称为无标度网络。这种网络通常表现为少数节点往往具有很大的度，且特征路径长度一般很小。

1.2 基于原始法的危险品道路运输复杂网络模型

为最大限度保证抽象的网络能够体现网络的拓扑结构特性及道路交叉口之间的空间关系，本文采用原始法构建危险品道路运输复杂网络模型。

在城市道路网络中存在危险品运输道路网络G=(V,E,S)，其中，V是危险品运输网络G的节点集合，代表配送中心、需求中心和道路节点等实际意义的地点，若记V=m，表示危险品运输网络G中有m个节点，则V=v1,v2,v3,…,vm；E是危险品运输网络G的边集合，代表连接两地点之间道路的集合，包括高速公路、国道和城市道路等，若记E=n，表示危险品运输网络G中有n条边，则E=e1,e2,e3,…,en。边上的权值集合S表示任意两节点之间的距离，记做{si,j|i,j∈m}。如此，便将危险品运输道路网络简化成为一个赋权无向连通网络。

基于上述分析，根据原始法构建的危险品道路运输复杂网络模型具有以下特点：1)网络模型来源于真实世界，因此网络结构受制于真实网络；2)网络模型的节点均具有明确的空间位置和坐标；3)网络节点所能连接边的数量受道路条件和其周围环境影响，从而影响网络节点度的分布。

1.3 研究方法及流程

危险品运输网络是一个复杂系统，本文首先通过实际的道路交通网络资料构建其复杂网络模型；其次获取危险品运输网络的拓扑结构信息；最后计算网络的特征值，并依此判断和分析危险品道路运输网络的拓扑特性。总体包括4个阶段：数据准备、数据处理、特征值计算和特性分析。具体操作步骤如下。

步骤1：数据准备。针对研究对象，获取城市规划图和土地利用图等资料，并利用Arc-GIS软件完成数据的处理，得到基于原始法的危险品道路运输复杂网络模型。

步骤2：数据处理。根据危险品道路运输复杂网络模型构造网络拓扑邻接矩阵和距离邻接矩阵。拓扑邻接矩阵是指当网络中两个节点相连，则该节点对应邻接矩阵中的元素为1，反之为0，其中节点自身相连对应的邻接矩阵元素为0，即对角线元素赋值为0。距离邻接矩阵中对应的元素为两个节点之间的距离。与拓扑邻接矩阵一样，节点自身相连的距离邻接矩阵元素也为0。

步骤3：特征值计算。在Matlab R2008a环境下，使用拓扑邻接矩阵计算网络平均节点的度、网络平均聚集系数和度分布，使用距离邻接矩阵，结合Dijkstra算法计算节点对之间最短路径距离和网络特征路径长度。

步骤4：分析危险品道路运输网络拓扑特性。

流程图如图1所示。

2 大连市危险品道路运输网络特征值计算及分析

2.1 数据准备与处理

本文以大连市危险品道路运输网络为研究对象，利用Arc-GIS 10.0完成空间数据的处理过程，结合基于原始法的危险品道路运输网络模型构建方法，最终得到大连市危险品道路运输复杂网络模型，处理过程如图2所示，网络模型如图2c所示。

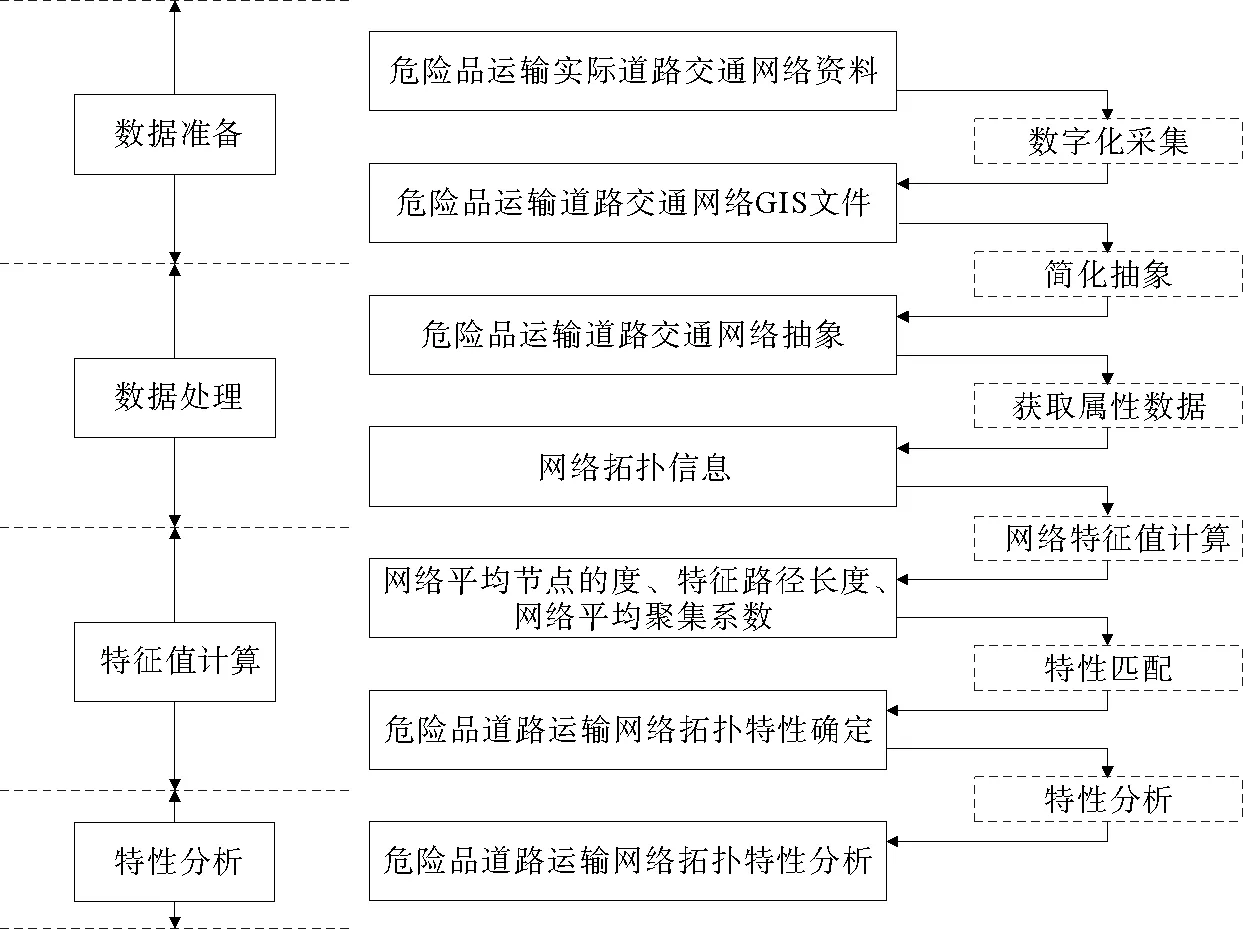
图1 危险品道路运输网络拓扑特性研究方法及流程Fig.1 Research method flowchart of topological properties on hazardous materials road transportation network

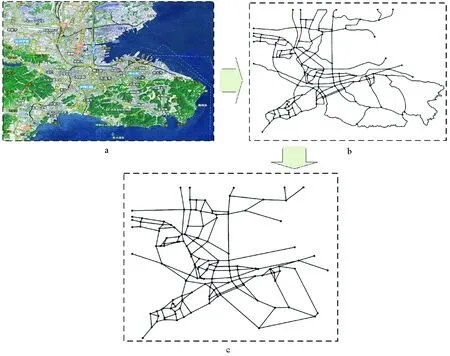
图2 大连市危险品道路运输网络模型处理过程Fig.2 Hazardous materials road transportation network model of Dalian

2.2 网络特征值计算结果

结合大连市危险品道路运输网络模型，在获取网络拓扑邻接矩阵和距离邻接矩阵的基础上，分别计算网络节点数、边数、网络平均节点的度、特征路径长度和网络平均聚集系数等网络特征值以及与其规模相同的随机网络特征路径长度和网络平均聚集系数，计算结果如表1所示。

表1 大连市危险品道路运输网络各参数计算表Tab.1 Parameters of hazardous materials road transportation network of Dalian

由表1可知，大连市危险品道路运输网络有道路节点154个，路段238条，网络平均节点的度约为3.090 9，介于3和4之间，说明危险品道路运输网络每个交叉口平均与3～4条路段直接相连。任意两个道路节点之间的平均距离为64.448 5km，两个节点之间最大的最短距离为193.387 1km。网络平均聚集系数越大，表明网络的连通性越好，相比文献[27]对城市道路交通网络的研究结果，危险品道路运输网络要略小一些。

2.3 网络特征值分析

2.3.1 节点度分布

对网络节点度分布的分析，有助于了解网络节点的空间分布情况和新增节点的接入规律。通过对大连市危险品道路运输网络模型的统计，其网络节点度分布概率图如图3所示。通过计算网络节点的度累积分布概率，并使用Matlab Curve Fitting工具箱进行数据拟合，网络节点度的累计分布概率图如图4所示。

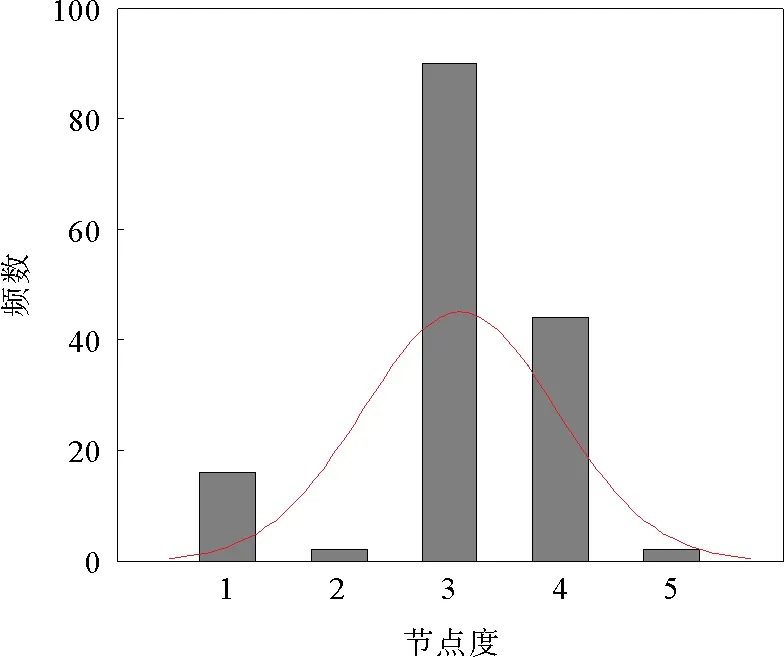
图3 网络节点度分布概率图Fig.3 Probability distribution of node degree

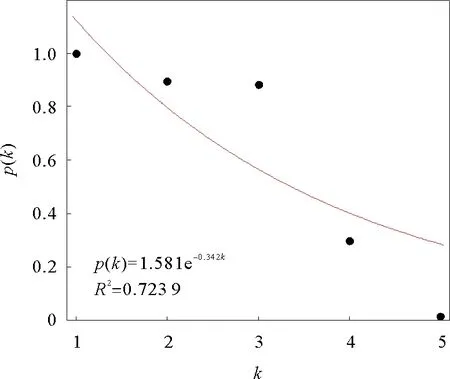
图4 节点的度累积分布概率图Fig.4 Probability distribution of cumulative node degree

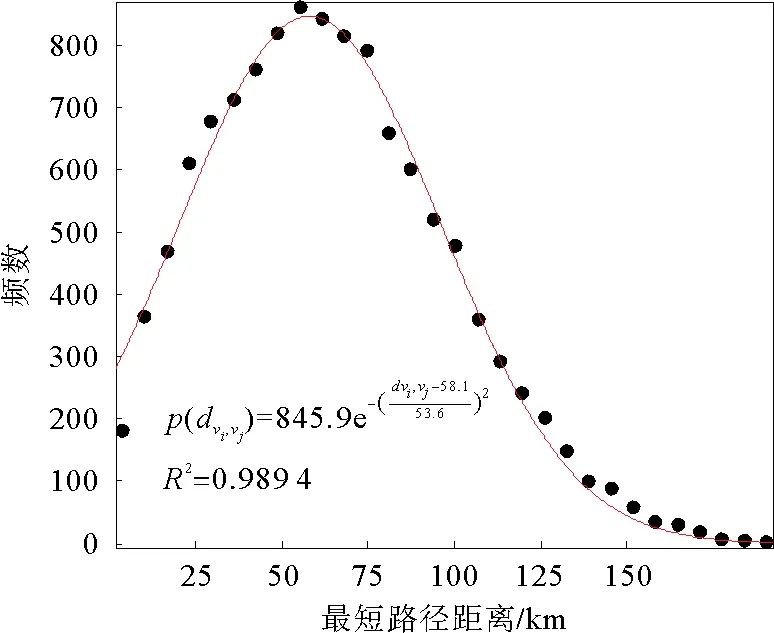
图5 最短路径距离分布概率Fig.5 Probability distribution of the shortest path distance

从图3可以看出，网络节点度分布概率大致服从正态分布，且分布不均匀。节点度最大值为5，说明危险品运输网络节点中，交叉口最多与5条路段相连。从图4可以看出，网络节点的度累积分布概率p(k)服从指数分布，拟合效果较好。由此可知，大连市危险品道路运输网络中新增节点与已存在节点之间的连接为随机连接，网络符合随机网络特性。

2.3.2 最短路径距离

最短路径距离反映了危险品道路运输网络各个节点之间的联系情况，本文对网络最短路径距离分布的统计结果如图5所示。

从图5可以看出，危险品运输道路网络最短路径距离的分布跨度较大，分布图近似呈正态分布，这说明虽然网络的拓扑结构规模可能不是很大，但网络却含有大量复杂的信息量，这为寻求改善和优化危险品道路运输网络结构提供可能。从图形总体来看，最短路径距离分布的期望值为58.1，这表明在危险品道路运输网络中，绝大多数节点对之间的最短路径距离和特征路径长度相差不是很大，可以用最短路径距离的期望值来表征网络特征路径长度，这为后面网络拓扑结构优化策略提供理论依据。

2.3.3 网络平均聚集系数和特征路径长度

网络平均聚集系数和特征路径长度是表征网络拓扑性质的重要指标。本文通过观察网络特征路径长度和网络平均聚集系数与网络增长的关系，以此研究危险品道路运输网络拓扑结构特性。相应统计结果如图6和图7所示。

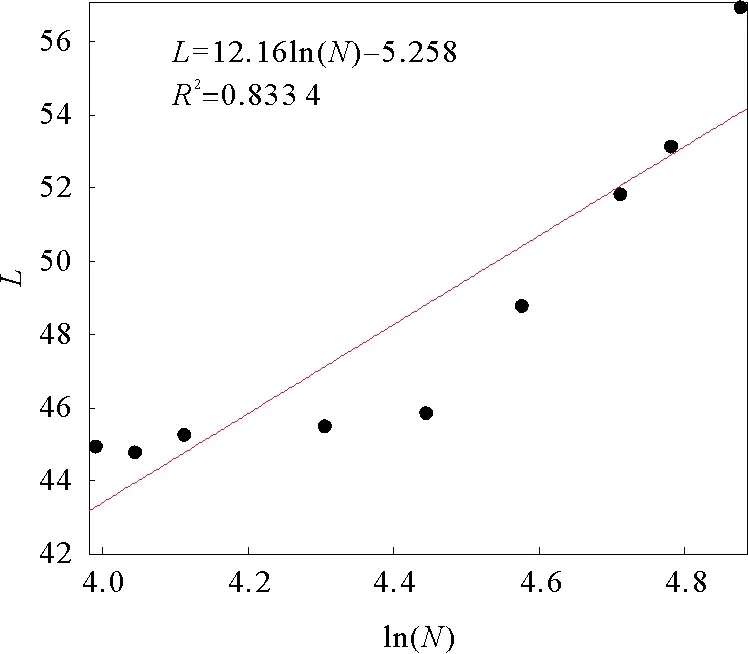
图6 特征路径长度随ln(N)增长变化曲线Fig.6 Curve of characteristic path length and ln(N)

图7 C/CR随网络节点数增长变化曲线Fig.7 Curve ofC/CRand network nodes

由表1的计算结果可知，L=15.392 2·LR，C=7.935 2·CR，这符合L≥LR与CCR的要求，表明大连市危险品道路运输网络拓扑结构具有小世界网络特性。

从图6可以看出，网络特征路径长度与节点数的对数值的线性关系拟合得较好，拟合曲线呈正比关系，这说明危险品道路运输网络在增长的过程中表现出路径长度较小的特点。从图7可以看出，C/CR比值随网络节点数的增长而增大，曲线拟合效果非常良好，这表明危险品道路运输网络规模越大，其网络拓扑结构的高度聚集特性越明显。由上述分析可知，大连市危险品道路运输网络具有较小的特征路径长度和较大的网络聚集系数，网络拓扑结构特性表现为小世界特性，是一种典型的小世界网络。

在复杂网络中，随机网络具有较小的特征路径长度而无明显聚集效应，这种网络连通性较差；无标度网络具有较小的特征路径长度和很大的网络平均聚集系数，但网络节点度分布服从幂律分布，网络抗毁性常常表现为蓄意攻击的脆弱性和随机攻击的鲁棒性。因此，这两种网络都不适宜作为危险品道路运输网络拓扑结构的发展模式。小世界网络较小的特征路径长度可确保配送的快速性和便捷性，而较大的网络平均聚集系数又有利于提高网络的层次结构性和随机、蓄意攻击下的抗毁性。因此，具有较小特征路径长度和较大网络平均聚集系数的小世界网络拓扑结构非常适合危险品道路运输网络，这为优化危险品道路运输网络拓扑结构提供依据。

3 危险品道路运输网络拓扑特性优化策略研究

依据本文提出的危险品道路运输网络拓扑特性研究方法及研究结果，主要从网络结构形态角度对危险品道路运输网络拓扑结构进行优化分析。具体地，将图2c所构建网络模型分为7个不同区域的局部网络，以此进行比较分析。划分情况如图8所示，相应的结构指标如表2所示。

结合表2数据，分别计算各局部网络的复杂网络特征值，结果如表3所示。

由表3可知，局部网络1～7的网络拓扑特性因平均路段长度的不同而不同。特别地，局部网络1和5出现了网络平均聚集系数为0的情况，网络失去小世界特性。这表明危险品道路运输网络的小世界特性与其形态结构关系密切，结合上述计算结果，本文分析如下。

1)危险品道路运输网络平均路段长度越大，网络的小世界特性越弱。如表3中，区域1和区域5的网络平均聚集系数值均为0，这说明网络不具备聚集效应，网络特性表现为随机网络特性。同等情况下，区域2的平均路段长度小于区域1，其网络拓扑特性表现为小世界网络。因此，通过降低危险品道路运输网络平均路段长度，可有效提高网络的小世界特性。

2)一定范围内，危险品道路运输网络平均路段长度较小的网络，其小世界特性越弱。在表3中，区域4的平均路段长度小于最小，但其网络平均聚集系数明显小于其他区域。

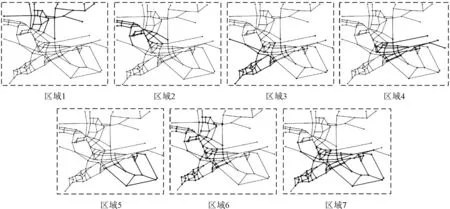
图8 大连市危险品道路运输网络局部示意图Fig.8 Local networks of hazardous materials road transportation network of Dalian

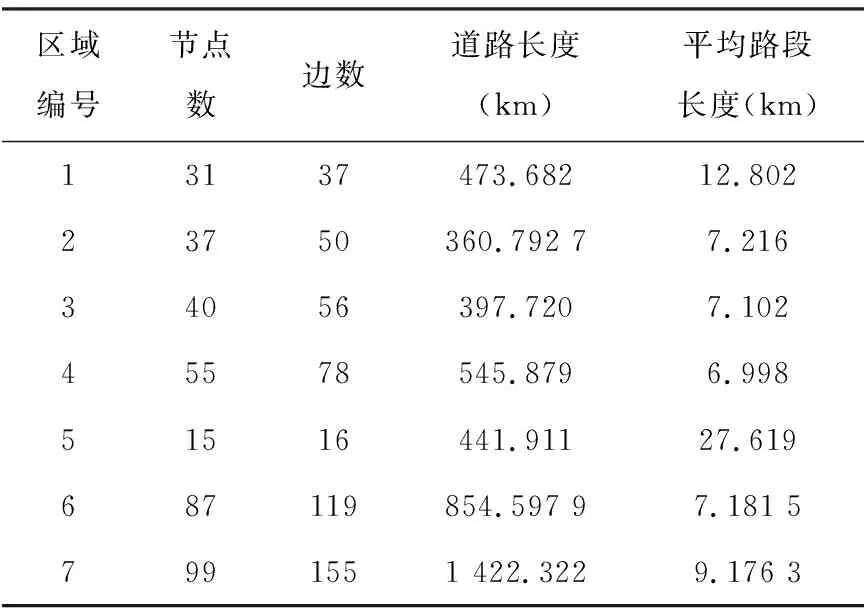
区域编号节点数边数道路长度(km)平均路段长度(km)13137473.68212.80223750360.792 77.21634056397.7207.10245578545.8796.99851516441.91127.619687119854.597 97.181 57991551 422.3229.176 3

表3 局部网络各参数计算表Tab.3 Parameters of local network

3)相近条件下(网络规模和网络特征路径长度等)，降低网络平均路段大小可提升网络小世界特性。在图8中，区域2和区域3的网络规模和特征路径长度相近，但区域3的网络平均路段长度小于区域2，其网络平均聚集系数也较大。因此，相同网络规模下降低网络平均路段大小可有效提高网络的小世界特性。

4)局部网络通过扩大网络规模可提升网络小世界特性。在图8中，区域7是区域3或区域4经过扩展后的网络，但其网络聚集系数均大于它们，区域6与区域2、3及区域2与区域6的关系也可说明此情况。因此，通过扩大网络规模，可提升网络的小世界特性。

5)采用疏密结合的拓扑结构方式，可提升网络的复杂网络特性。由图8不难看出，区域1和5的网络结构最为疏散，区域4的网络结构最为紧密，而区域3、6和7的网络结构疏密差异较大，但它们的网络平均聚集系数大于其它网络。因此，采用疏密结合的布局方法可有效提高危险品道路运输网络的小世界特性。

4 结论

本文以危险品道路运输网络为研究对象，运用复杂网络理论研究网络的拓扑特性及优化策略，主要得出以下结论：

1)危险品道路运输网络特征值与一般道路交通网络存在较大差异，这些特征值可为计算机模拟危险品道路运输网络生长规律提供参数依据。

2)危险品道路运输网络节点度分布服从正态分布，累积分布服从指数分布，网络拓扑特性具有随机网络特性。

3)危险品道路运输网络最短路路径距离分布服从正态分布，这表明虽然危险品道路运输网络规模不是很大，但信息量较为复杂，且绝大多数节点对之间的最短路径距离和特征路径长度相差很小，这种特殊网络拓扑结构特性为改善危险品道路运输网络结构提供可能性。

4)危险品道路运输网络是一种典型的小世界网络，危险品道路运输网络所表现出的拓扑特性与绝大多数交通运输网络相似，积极保持网络的小世界特性是有助于提高网络效能。

5)危险品道路运输网络具有较小的特征路径长度和较大的网络平均聚集系数，但相比城市道路交通网络，其具体表现为特征路径长度太大和网络平均聚集系数太小的特性，因此提高网络聚集系数和降低特征路径长度是优化危险品道路运输网络拓扑特性的有效措施。

6)危险品道路运输网络的形态结构影响其复杂网络特性的表现。相近条件下(网络规模和网络特征路径长度等)降低网络平均路段大小、扩大局部网络规模和采用疏密结合的布局方法等都可以增强危险品道路运输网络的小世界特性，提升网络节点之间的连通效率，使网络表现出一定的模块性和层次性。

当然，本文是在一些简化的基础上对危险品道路运输网络的拓扑结构进行研究，这和现实情况还存在一定的差距，因此改进网络模型构造方法和在更广泛的危险品道路运输网络中进行实证研究是下一步进行的工作。