冲击荷载下纤维砂浆动态受压特性
2018-02-27田正宏江桂林苏伟豪
田正宏, 江桂林, 苏伟豪, 倪 军
(1.河海大学 水利水电学院,南京 210098; 2.中国水利水电第七工程局有限公司,成都 610081)
掺纤维水泥基复合材料是目前常见工程材料。若干研究证明其具有很好的增韧、抗裂效果[1-3]。但这类材料在承受动态荷载作用下的性能研究多集中在碳纤维、钢纤维水泥基复合材料上[4-6]。PVA水泥基复合材料动态力学特性研究较少,尚未取得一致可信的结论[7-8]。而采用超高分子量聚乙烯(UHMWPE)纤维砂浆在冲击荷载下的力学性能研究仍处于空白。因此研究新型纤维(UHMWPE和PVA)砂浆在高应变率下的动态受压性能具有重要的意义。
已有纤维砂浆在冲击荷载作用下的力学特性研究大都基于试验分析,理论研究还有待深入,尤其是考虑宏观损伤的纤维砂浆本构关系并未给出简明合理的计算模型。本文采用直径为74 mm分离式霍普金森杆装置对四种砂浆进行动态压缩力学性能试验,分析加载应变率对试样强度、韧性等特性指标影响,并通过破坏形态和极限韧性等指标判断纤维砂浆受压综合性能;基于宏观损伤因子探讨了传统非线性黏弹性本构模型简化方法进而提出四参数模型,并分析参数对纤维性能的影响。
1 试验概况
1.1 试验材料
海螺牌P.O42.5水泥;天然河砂,细度模数为2.8;自来水,UHMWPE纤维由荷兰(上海)DISMAN公司生产,呈白色纤维束状,如图1(a)所示;国产PVA纤维为皖维牌高强高弹模纤维,呈淡黄纤维束状,如图1(b)所示; 另一PVA纤维由日本可乐丽公司生产,呈白色纤维束状,经表面处理后质地较硬,如图1(c)所示。纤维物理参数见表1。

(a) UHMWPE
(b) 国产PVA

(c) 日产PVA
1.2 试验配合比
各组砂浆质量配合比均为水∶水泥∶砂=1∶2∶4,其中水的质量为230 kg/m3。A组为素砂浆,B、C、D组分别为掺加1.8 kg/m3的UHMWPE纤维、国产PVA纤维、日产PVA纤维砂浆。
1.3 试件制作
采用直径75 mmPVC管模浇筑试件,置于振动台振动密实后,试件表面用塑料膜覆盖保湿养护;48 h后拆模,采用饱水法养护;90 d后切割加工成高37 mm试样进行动态压缩试验。

表1 纤维物理参数
2 分离式霍普金森压杆试验
2.1 冲击试验原理
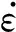
(1)
(2)
(3)
式中:Ab,Eb,C0分别为杆的横截面面积,弹性模量与波速;l,As为试件沿杆方向的长度与横截面面积。
为保证试件内部应力均匀分布,整形技术已被广泛应用于脆性材料SHPB试验中[10-12]。子弹先冲击放置于入射杆前端的整形材料,如图2所示。使用整形片能消除加载过程中应力波的振荡,这样修正后产生的应力波在入射杆中传播,且试件内部也会达到应力平衡状态。本文选用紫铜片作为整形片,其尺寸:直径为2 mm,厚度为0.9 mm。通常根据应力均匀假设来检验砂浆水泥基试件在试验过程中是否满足应力均匀分布的要求[13],如图3所示。由图3可知,试样内部基本达到应力均匀状态(满足εi+εr=εt)。
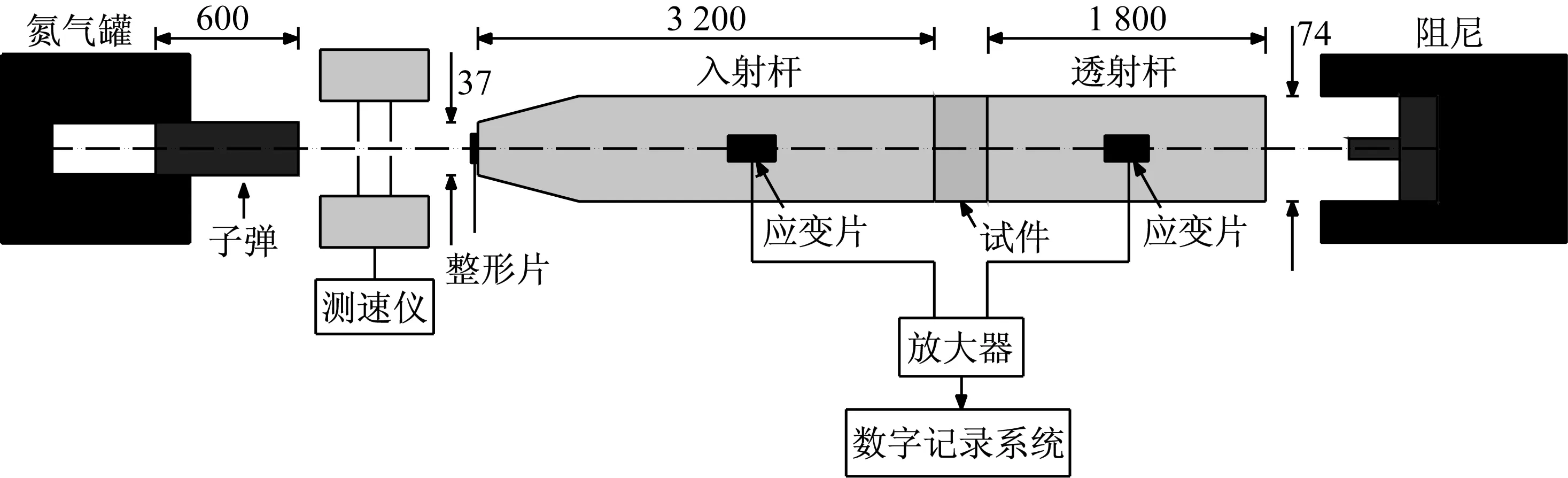
图2 SHPB装置动态压缩示意图(mm)
2.2 试验方案
每组砂浆均采用0.30 MPa、0.35 MPa、0.40 MPa、0.45 MPa、0.50 MPa五种不同气压加载,使子弹以不同速度冲击入射杆从而产生5种应变率;各组砂浆相同工况均重复5次冲击试验。数字示波器记录入射波、反射波和透射波信号,提取各自波形分析即可得到试验的应力—应变曲线和加载应变率。
大多数学者均认为SHPB试验实现近似应变率是由有效加载时间内在反射应力波上得到一个近似恒定平台来表征的[14-15],据此,选取各组砂浆在相同工况下5次冲击试验中反射波出现最接近平台的试验作为有效试验,认为试验过程中达到近似恒定应变率,其中B组在0.30 MPa气压下最接近平台的反射波,如图4所示。本文采用峰值应力处应变率作为动态荷载作用下试件应变率代表值,如图5所示。
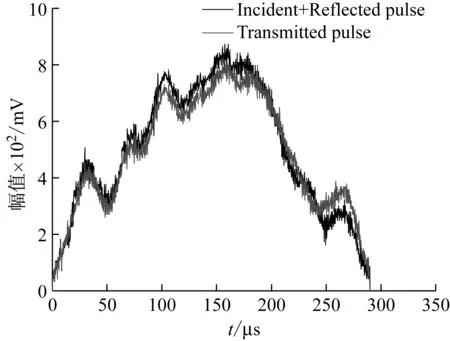
图3 应力均匀性验证
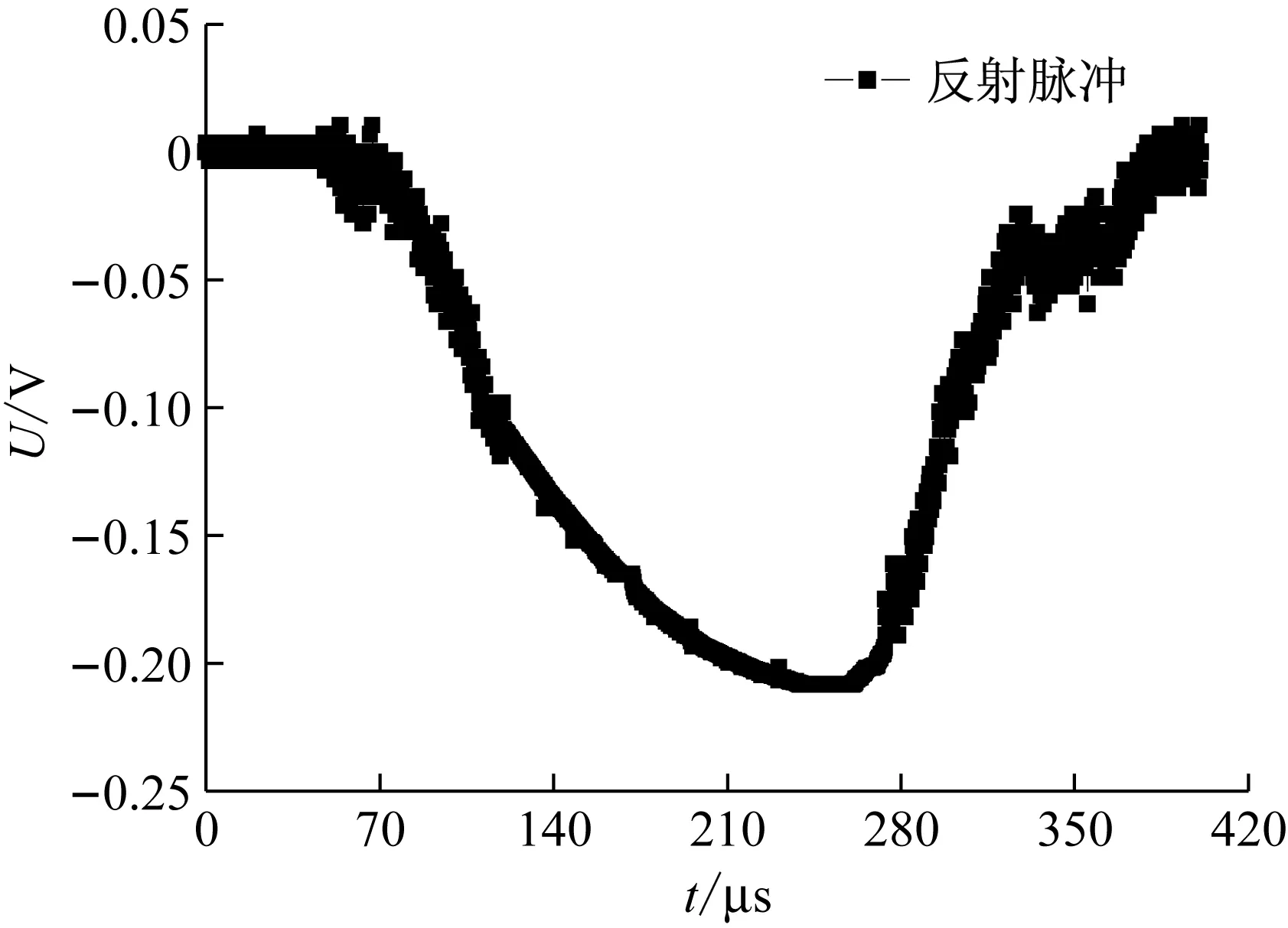
图4 近似恒应变率验证
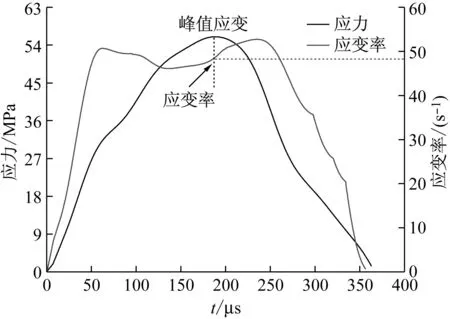
图5 应变率代表值确定示意图
Fig.5 Determination of representative value of strain rate schematic diagram
3 试验结果与讨论
3.1 破坏模式
各组砂浆在上述五种气压加载下其动态破坏模式如图6所示。其中A、B、C、D分别表示素砂浆、UHMWPE纤维砂浆、国产PVA纤维砂浆、日产PVA纤维砂浆,下同。
图6可知,随应变率增加,各组砂浆破裂程度均显著增加。砂浆在动态荷载下破坏情况表明碎块大小及数量与应变率紧密相关:施加应变率越大,破碎程度越高。从破坏形态可以看出,相同动态荷载下,UHMWPE纤维阻裂、增韧效果强于日产PVA纤维,而日产PVA纤维则强于国产PVA纤维,国产PVA纤维效果略优于素砂浆。纤维增强抗冲效果的宏观机理是由于动态加载下裂缝穿过骨料以较短较直的路径传播,而纤维桥接作用部分改变砂浆试样阻裂传递路径和增加侧向约束,延缓裂缝扩展速率进而提高试件韧性。但随着应变率的增加,某固定含量纤维约束作用则逐渐减弱。
3.2 应力应变曲线与韧性
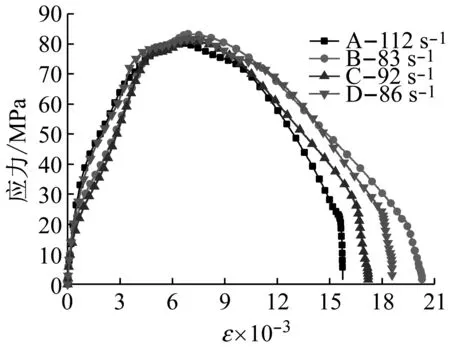
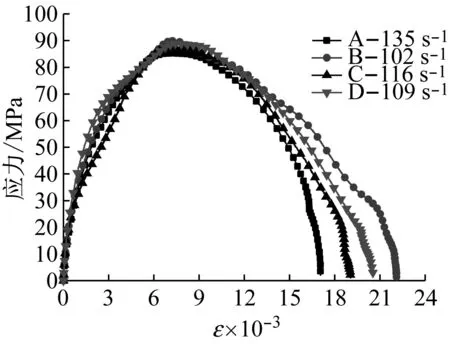
不同应变率下,各组砂浆的应力-应变曲线如图7所示,其中图中每条曲线是5次冲击试验中反射波出现最接近平台试验的应力应变曲线。
通过应力-应变曲线,可以得到砂浆性能参数如表2所示。其中0.30~0.50表示加载气压分别为0.30 MPa、0.35 MPa、0.40 MPa、0.45 MPa、0.50 MPa。峰值韧性是指应力-应变曲线在峰值应力前包络的面积,极限韧性是指整个应力-应变曲线的包络面积。
由表2可知,在相同冲击气压下,纤维砂浆应变率较素砂浆小,但其抗压强度较素砂浆大,可知UHMWPE纤维砂浆的应变率效应最弱,但其抗压强度最大;各组砂浆的抗压强度、峰值应变、极限应变、峰值韧性和极限韧性随着应变率的增加而增加,但极限韧性随应变率增加的幅度最大,表明其应变率效应最明显。
3.3 机理分析
国产PVA纤维由于不易分散,因此冲击过程中裂缝易出现在纤维与砂浆结合薄弱处,在较低应变率下会产生大量的微裂缝甚至少量的碎片,导致纤维增韧阻裂整体效果不是很明显,这与表2中其极限韧性很小略大于素砂浆相吻合。
日产PVA纤维表面经过特殊化处理,质地较硬,直径较国产PVA纤维大,在砂浆中更易均匀分散。纤维砂浆破坏时吸收能量要高于国产PVA纤维砂浆。故其增韧效果优于国产PVA纤维。
UHMWPE纤维特点是具有很高弾性模量,纤维体吸收能量显著增强。在低应变率下无需试件以破裂成碎片的形式来消耗冲击能量,但试件内部易产生许多微裂缝。高应变率作用下外部冲击能量大,当UHMWPE纤维达到极限应变时吸收的能量不足以抵消冲击能量时,试块则转而以破碎裂片来抵消剩余能量。结合试件动态破坏形态和砂浆试件吸收能量可知,UHMWPE纤维砂浆优于日产PVA纤维砂浆。





综上可知,各组砂浆抗压综合性能排序:UHMWPE纤维最优,日产纤维次之,国产PVA纤维优于素砂浆。
4 动态损伤本构模型
4.1 本构模型
朱-王-唐(ZWT)本构模型最初主要是针对高聚物材料提出的一种本构关系[16]。由于水泥基类材料具有率敏感性,因而高应变率下的实验曲线出现明显迟滞黏弹性行为。该模型也常被扩展用来描述砂浆的率型本构[17]。
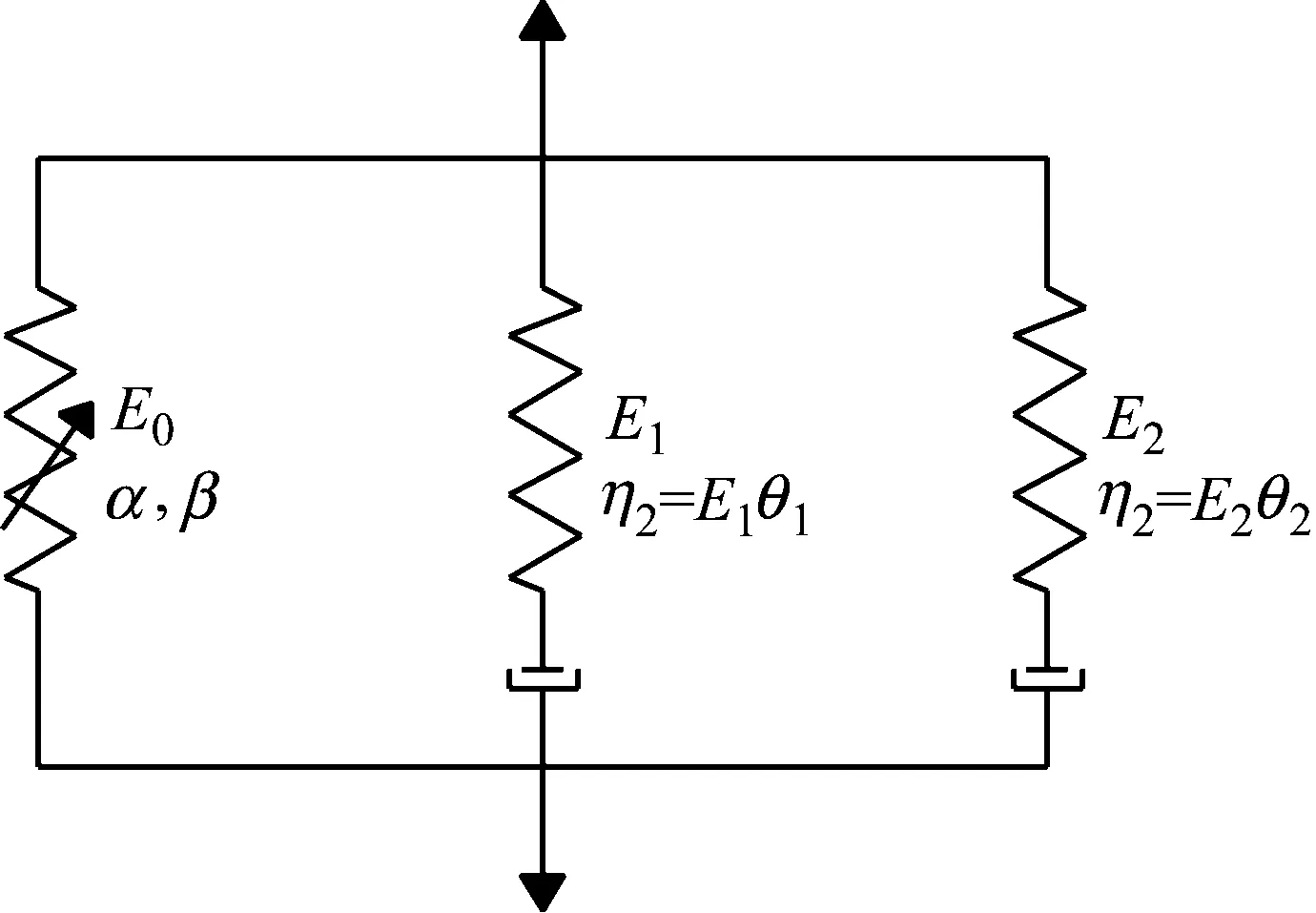
ZWT本构模型由一个非线性弹簧和两个不同特征时间的Maxwell体并联组成,如图8(a)所示,其本构方程式(4)
(4)
其中E0、α、β为对应的弹性常数。用两个积分公式分别代表在低应变率和高应变率下不同的黏弹性行为。E1和θ1分别是低频Maxwell体的弹性模量和特征时间,E2和θ2分别是高频Maxwell体的弹性常数和特征时间。根据陈江瑛等的研究,在时间尺度以10-6~10-4s计的冲击加载条件下,具有松弛时间θ1的低频Maxwell单元将无足够的时间来松弛,此时低频Maxwell单元化为弹性常数为E1的弹簧,如图8(b)所示。则ZWT方程简化为式(5)
(5)
胡时胜等[18]考虑到砂浆材料变形量很小,引入损伤因子D,改进本构方程写为
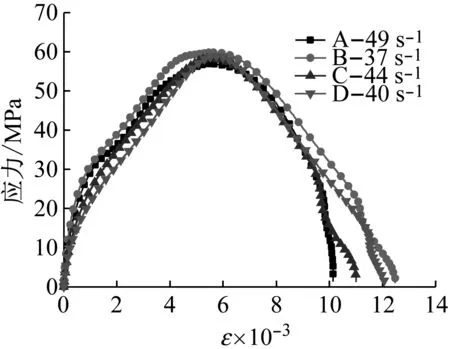
(a) 0.3 MPa

(b) 0.35 MPa
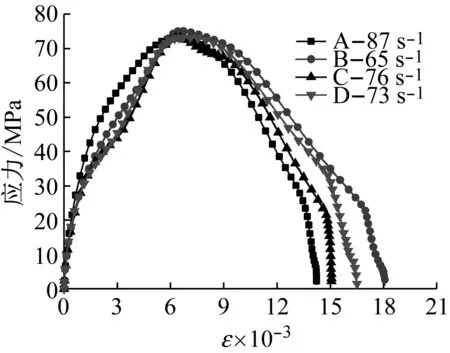
(c) 0.40 MPa
(d) 0.45 MPa
(e) 0.50 MPa
图7 各组砂浆的应力-应变曲线
(a) ZWT本构模型
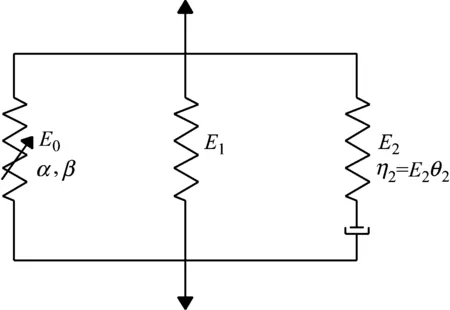
(b) 高频ZWT本构模型
(6)
式(6)中:σ为试件内真实应力,σr为材料无损伤时的应力。
4.2 损伤因子建立
Wang等[19]利用下式来描述累积速率与应变率非线性关系见式(7)
(7)
对式(7)进行时间变量积分得式(8)
(8)
式(8)ζ=λ-1,再考虑初始情况:
D|ε=0=0
(9)
得D1=0,故整理得式(10)
(10)
文献[17]研究表明λ≈1,得ζ=0,即假设损伤因子D与应变呈正比关系。
故
D=D0·ε
(11)
4.3 本构模型讨论
将损伤因子D的表示式代入式(6),考虑SHPB试验应变率近似恒定,最终砂浆动态受压本构方程写成
(12)
其中E3=E0+E1。本文对各组砂浆所有工况均进行相关拟合,本构方程拟合采用D0,E3,E2和θ2四个参数。具体结果见表3所示。其中D0为损伤演化速率;E3为与应变率无关的弹性模量;E2为高频Maxwell体的弹性常数;θ2为特征时间。
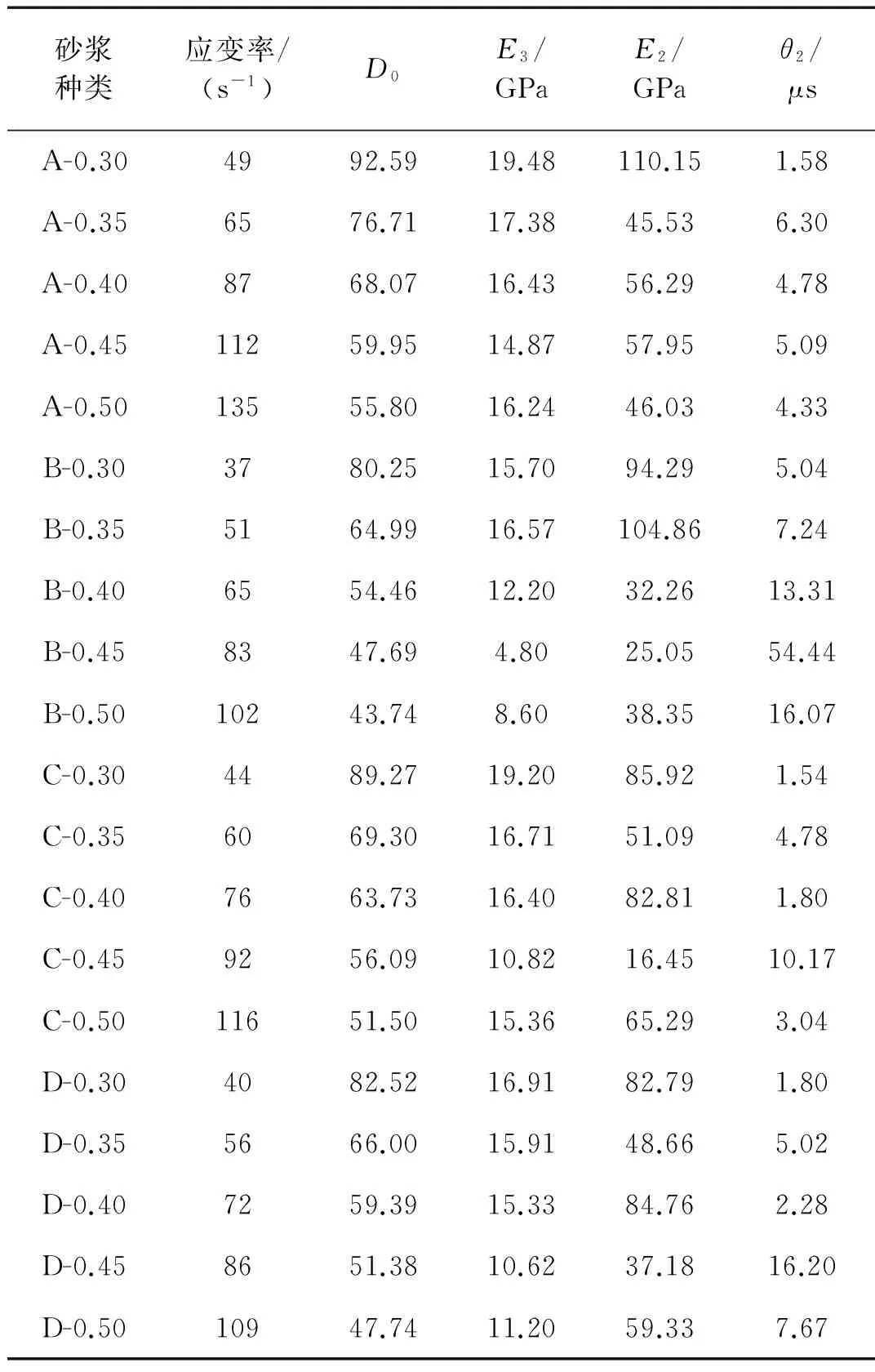
表3 各组砂浆本构模型中参数拟合结果
由表3可知:随着应变率的增加,各组砂浆的损伤演化速率D0值逐渐减小,这与高应变率下裂缝来不及扩展理论相一致,且B组砂浆损伤演化速率D0最小,即UHMWPE纤维阻裂效果最好;同样,随着应变率的增加,各组砂浆与应变率无关的弹性模量E3大体均呈逐渐减小的趋势;B组砂浆特征时间θ2最大,也表明UHMWPE纤维增韧效果最好,受应变率响应最弱。
各组砂浆试验值与拟合值的比较,如图9所示。由图可知:经简化四参数本构模型可以很好地模拟各组砂浆动态应力应变关系,且相关系数在0.98以上。
5 结 论
(1) 砂浆材料均有应变率效应,但纤维砂浆应变率效应较素砂浆弱,其中UHMWPE纤维砂浆应变率效应最弱。
(2) 冲击荷载下纤维砂浆抗压强度、极限应变、峰值应变、峰值韧性和极限韧性均随着反应率的增加而提高,极限韧性应变率效应最明显。
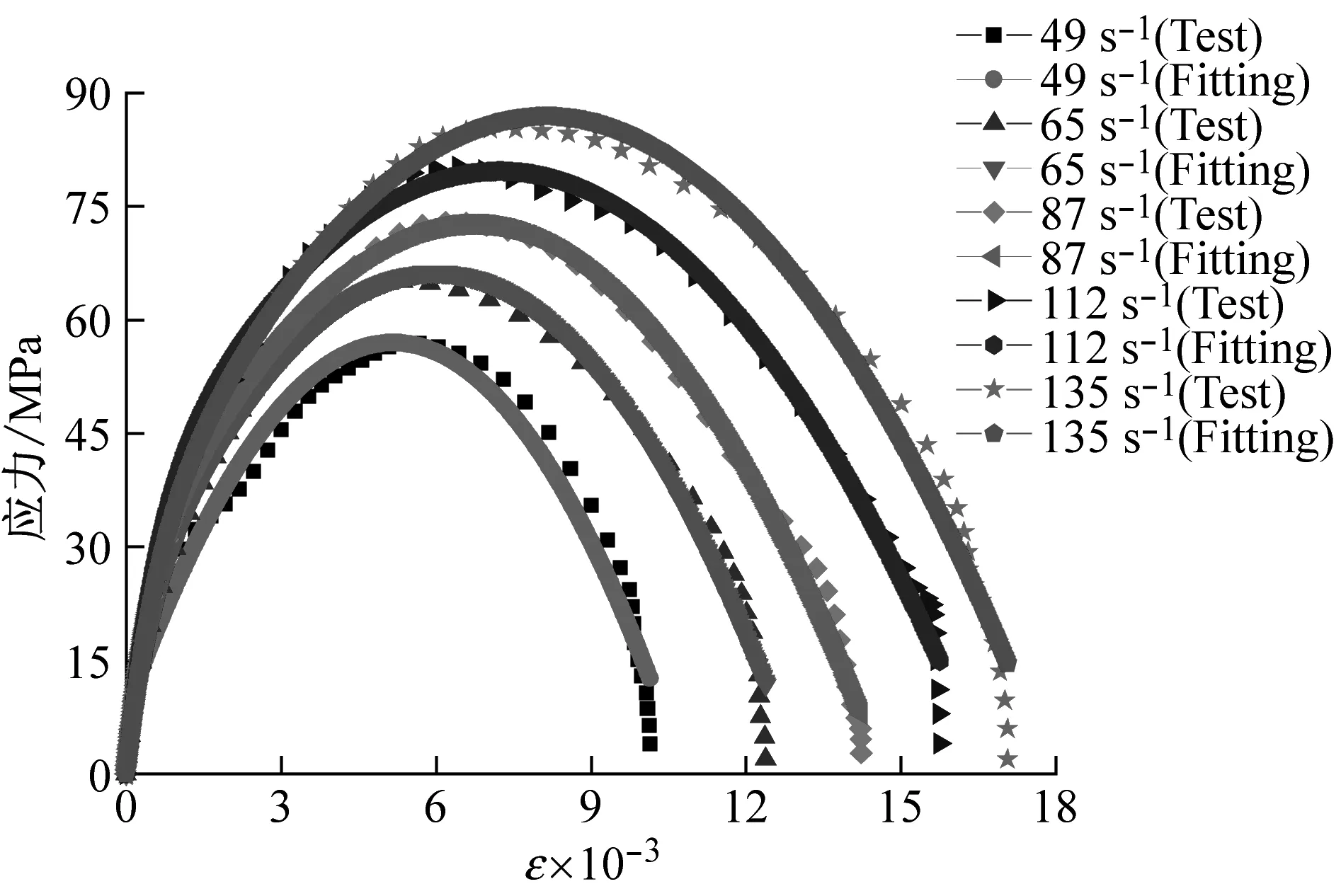
(a) A组
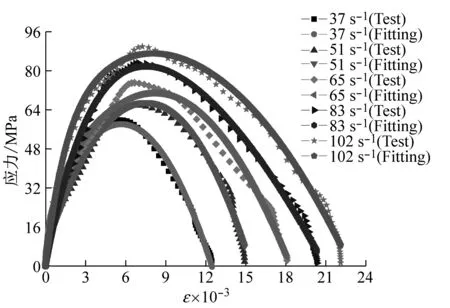
(b) B组
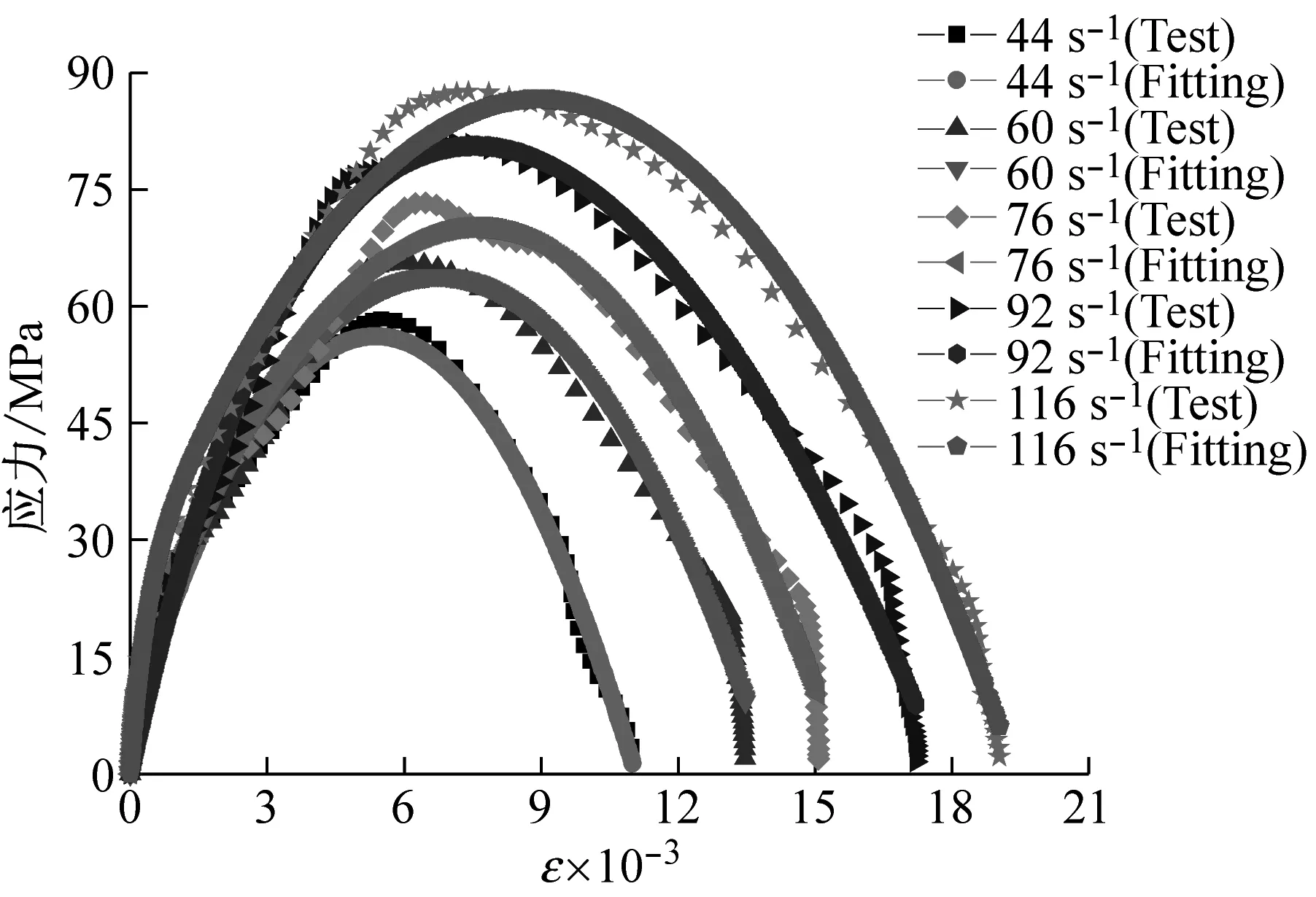
(c) C组
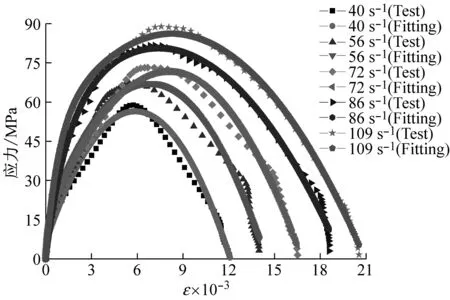
(d) D组
(3) 冲击荷载下UHMWPE纤维砂浆综合性能最优,日产纤维砂浆次之,国产PVA纤维砂浆最差,但略优于素砂浆。
(4) 本文提出四参数本构模型形式简单,且该模型可很好地模拟各组纤维型砂浆材料的动态受压应力-应变关系。
[1] CAVDAR A. A study on the effects of high temperature on mechanical properties of fiber reinforced cementitious composites [J].Composites, 2012, 43(5):2452-2463.
[2] KANG Q, FANG Y, DENG H. Mechanical properties and crack-resistance of cement mortar with basalt/polypropylene hybrid fiber[J]. Materials Review, 2011, 25:122-126.
[3] SOE K T, ZHANG Y X, ZHANG L C. Material properties of a new hybrid fiber-reinforced engineered cementitious composite [J].Construction and Building Materials, 2013, 43(3):399-407.
[4] JAROSLAW B, BARBARA S, PATRYK J. The comparison of low velocity impact resistance of aluminum/carbon and glass fiber metal laminates [J]. Polymer Composites, 2014, 37(4):1056-1063.
[5] SOUFEIANI L, RAMAN S N, JUMAAT M Z B, et al. Influences of the volume fraction and shape of steel fiber-reinforced concrete subjected to dynamic loading—A review [J]. Engineering Structures, 2016, 124: 405-417.
[6] JIAO C, SUN W, SHI H, et al. Behavior of steel fiber-reinforced high-strength concrete at medium strain rate [J].Frontiers of Architecture and Civil Engineering in China,2009,3(2):131-136.
[7] BAO W B, ZHANG S F, DI G H, et al. Dynamic load effects of PVA tail sand cement base composite materials[J].Applied Mechanics and Materials,2014,518:66-70.
[8] CHEN Z, YANG Y, YAO Y, et al. Effect of water binder ratio on dynamic mechanical properties of PVA fiber reinforced cement-based composite [J]. Romanian Journal of Materials,2012,42(3):256-263.
[9] ROSS C A, THOMPSON P Y, TEDESCO J W. Split Hopkinson pressure bar tests on concrete and mortar in tension and compression[J].ACI Material Journal,1989,86(5):475-481.
[10] DAI F, HUANG S, XIA K, et al. Some fundamental issues in dynamic compression and tension tests of rocks using split Hopkinson pressure bar [J]. Rock Mechanics and Rock Engineering, 2010, 43:657-666.
[11] CHEN Xudong, WU Shengxing, ZHOU Jikai. Quantification of dynamic tensile behavior of cement-based materials[J]. Construction and Building Materials, 2014,51:15-23.
[12] CHEN Xudong, GE Limei, ZHOU Jikai, et al. Experimental study on split Hopkinson pressure bar pulse-shaping techniques for concrete[J]. Journal of Materials in Civil Engineering,2016,28(5):04015196.
[13] 李为民, 许金余, 沈刘军,等. Φ100 mmSHPB应力均匀及恒定应变率加载试验技术研究[J].振动与冲击,2008,27(2):129-132.
LI Weimin, XU Jinyu, SHEN Liujun, et al. Study on 100-mm-diameter SHPB techniques of dynamic stress equilibrium and nearly constant strain rate loading[J].Journal of Vibration and Shock,2008,27(2):129-132.
[14] FREW D J, FORRESTAL M J, CHEN W. Pulse-shaping techniques for testing brittle materials with a split Hopkinson pressure bar [J]. Experimental Mechanics, 2002,42(1):93-106.
[15] 赵习金, 卢芳云, 王悟,等. 入射波整形技术的实验和理论研究[J].高压物理学报,2004,18(3):231-236.
ZHAO Xijin, LU Fangyun,WANG Wu, et al. The experimental and theoretical study on the incident pulse shaping technique[J].Chinese Journal of High Pressure Physics,2004,18(3):231-236.
[16] 杨黎明, 朱兆祥, 王礼立. 短纤维增强对聚碳酸酯非线性黏弹性性能的影响[J]. 爆炸与冲击,1986,6(1): 1-9.
YANG Liming, ZHU Zhaoxiang, WANG Lili. Effects of short-glass-fiber reinforcement on nonlinear viscoelastic behavior of polycarbonate[J]. Explosion and Shock Waves,1986,6(1):1-9.
[17] 陈江瑛, 王礼立.水泥砂浆的率型本构方程[J].宁波大学学报,2000,13(2):1-5.
CHEN Jiangying, WANG Lili. Rate-dependent constitutive equation of cement mortar[J].Journal of Ningbo University(Natural Science and Engineering),2000,13(2):1-5.
[18] 胡时胜, 王道荣, 刘剑飞. 混凝土材料力学性能的实验研究[J].工程力学,2001,18(5): 115-118.
HU Shisheng, WANG Daorong, LIU Jianfei. Experiment study of dynamic mechanical behavior of concrete[J].Engineering Mechanics,2001,18(5):115-118.
[19] WANG L L, ZHOU F H, SUN Z J, et al. Studies on rate-dependent maro-damage evolution of materials at high strain rates[J].International Journal of Damage Mechanics,2010,19:805-820.
