基于CEL算法的发动机润滑液瞬态振荡过程可视化研究

马子远， 俞小莉， 黄钰期， 刘震涛， 黄 瑞

(浙江大学 能源工程学院， 杭州 310000)

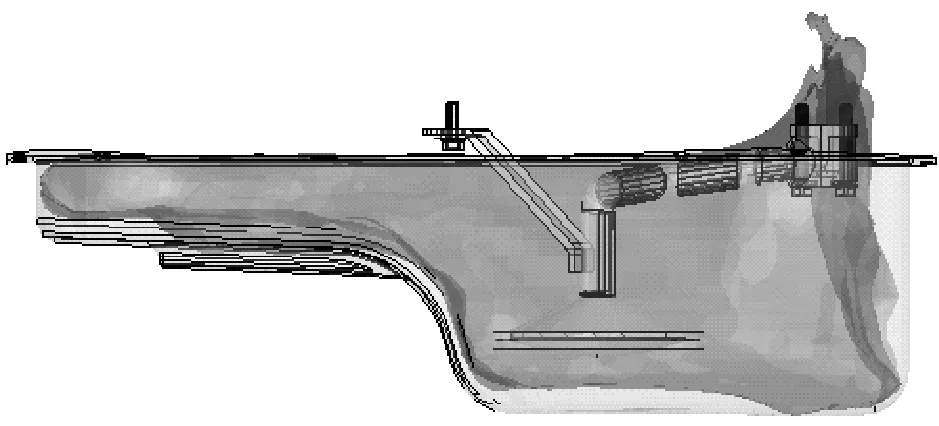
在内燃机中，油底壳主要作为一个储存润滑油的容器，并通过其吸入系统将润滑油供应到发动机部件上，并直接影响到发动机的工作性能。油底壳中的总油量是根据发动机中润滑旋转部件所需的油流量及满足整个润滑系统循环所需的油流量来确定[1]。一个通用的发动机油底壳-吸油-过滤器系统，如图1所示。

油底壳设计的重要目标是既要满足基于发动机整体设计标准的NVH性能，同时还要满足车辆设定工况(操作工况)下的润滑性能，这都与油底壳内的润滑油振荡情况有关[2]。油底壳中润滑油随机体振荡是一个涉及多体动力学、弹塑性力学及流体力学等多学科的问题，也是一个典型的流固耦合振荡问题。目前随着数值计算技术的飞速发展，一些新型的数值计算方法(如SPH法、ALE法、混合CFD法等)为解决复杂的流固耦合问题提供了强大的技术支持，尤其是为振荡CFD问题的深入研究开辟了新的方法[3]。

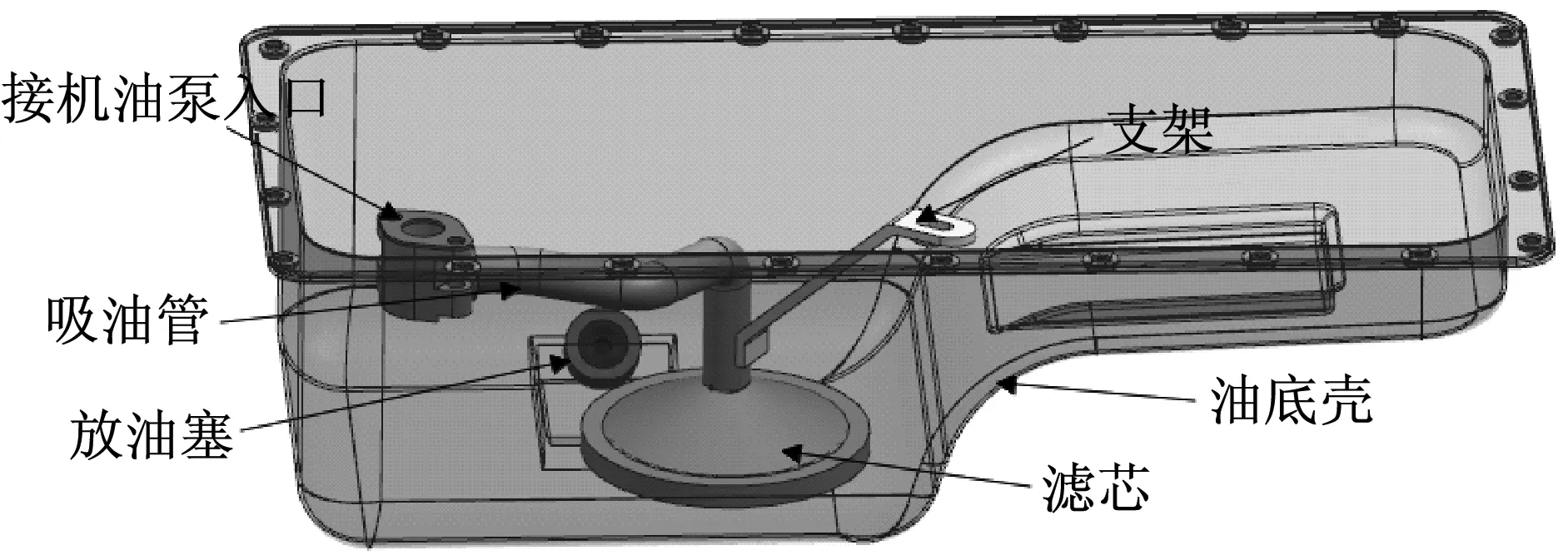
图1 油底壳吸油-过滤-壳布局

拉格朗日算法(Lagrangian)以物质的坐标为基础，有限元网格的节点即为物体的质点，可以跟踪质点的运动轨迹，从而能准确地描述物体边界的运动;但是在涉及大变形的问题时，单元网格将会出现严重的畸变现象，其可能最终会导致无法继续计算。欧拉方法(Eulerian) 常用于流体力学计算分析，计算中所采用的网格以空间坐标为基础，有限元节点即为空间点，因此能够处理物质的扭曲及一些大变形问题，但由于欧拉法在捕捉物体边界信息上较为困难，不能够精确描述物质的边界，并且该方法固存的数值耗散问题导致其对计算资源和时间要求较高[4]。单纯的拉格朗日和单纯的欧拉算法都有各自的缺陷和不足，但是又有着各自的优势。如果将两者有机地结合起来，可以解决一些只用单一方法所不能解决的问题。耦合的欧拉-拉格朗日(Coupled Lagrangian Eulerian，CEL) 方法就是基于这一目的最早由Noh[5]提出的，并采用有限差分法求解了带有移动边界的二维流体动力学问题。在Noh的研究中，网格点可以随物质点一起运动，但也可以在空间中固定不动，甚至网格点可以在一个方向上固定，而在另一个方向上随物质一起运动。因此，CEL算法在解决物体的大位移时，比如碰撞、流体动力学及流体-固体之间的相互作用时有强大的优势。图2为Lagrangian算法、Eulerian算法及CEL算法在相同时间Δt上的物体形态与空间网格变形状态示意图。

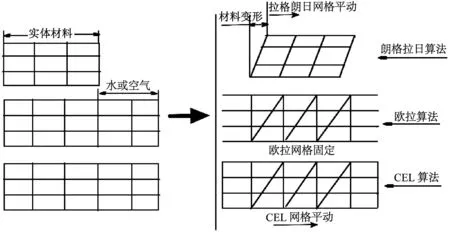
(a)t时刻 (b)t+Δt时刻

图2 3种算法对应的网格变形特点

Fig.2 Characteristics of deformed meshes of Lagrangian, Eulerian and CEL algorithms

耦合欧拉-拉格朗日(CEL)方法对流固耦合振动数值仿真研究提供了一种新的思路，其本质上是以欧拉材料域在受拉格朗日部件运动影响下的流动特性作为研究对象的，不受网格运动的限制[6]，因此在振荡流计算方面具有独特优势。

鉴于CEL方法在处理此类问题方面的优势，目前国内外已有不少学者开展了耦合欧拉-拉格朗日方法(CEL)的研究，Foucard等[7]采用了CEL算法对大变形或极端变形情况下的超弹性材料问题进行了计算分析，采用扩展有限元(XFEM)方法来对系统力学平衡方程和变形梯度张量方程进行了离散化，并提出了一种适应于材料属性介于流体和固体之间的物体的运动的计算方程；Rostami等[8]采用CEL方法来模拟两相纳米流(流体中包含AL2O3粒子)，对其在微通道波纹管内的共轭流动换热问题进行了研究；Diggs等[9]对采用CEL方法研究多相流问题中的体积分数计算提出了评价方法，并对基于网格法和基于粒子法两种方法进行了对比研究； Bahremand等[10]采用CEL方法对定常壁面热流条件下的螺纹管内的纳米流湍流流动问题进行了数值模拟和试验测试；Vujanovi等[11]采用CEL法对柴油机的喷雾、燃烧及污染物的生成过程进行了数值模拟，并与已有的实验结果进行了对比，研究显示CEL方法在解决此类问题上有明显优势，同时具有高的计算效率和计算精度；Jarauta等[12]采用嵌入式CEL方法对高分子聚合物燃料电池电解质气道内的水滴动态特性进行了数值研究，并与实验数据进行了对比分析。

在国内，叶林征等[13]为探究超声珩磨中不同角度空化微射流冲击下壁面特性的变化，采用CEL算法进行了模型的模拟和分析；卿启湘等[14]针对盾构机切刀切削土体仿真收敛困难，仿真结果震荡严重等复杂非线性问题，利用CEL法对模型进行了求解，并与理论公式计算结果进行了对比，发现CEL方法在处理此类问题时收敛快，震荡小，计算效率高，对网格大小敏感性低，结果更接近理论解；姚小虎等[15]采用CEL算法分析了复杂的水陆两栖飞机水上降落时，机头入水瞬时的结构动力响应；王建华等[16]根据模拟钻井船在黏土层中插桩对邻近桩影响的离心模型试验结果，验证了通过CEL方法结合非线性地基梁有限元计算方法来分析此类问题的可行性。

1 数值分析模型

1.1 系统描述

分析系统为新设计开发的深井后置式4缸柴油发动机的油底壳系统。系统横截面，如图3所示。

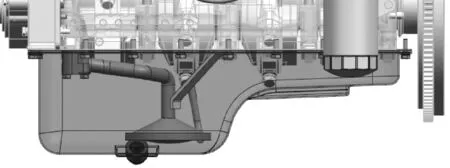
图3 发动机的横截面图

分析的系统模型参数如表1所示。

油底壳作为拉格朗日部件，润滑油区域划分为欧拉网格。采取CEL方法计算模型时，欧拉网格立方体模型与油底壳相比要确保足够大，以保证欧拉材料的自由流动和在润滑液的振荡高度。计算的材料参数如表2所示。

表1 算例系统计算参数

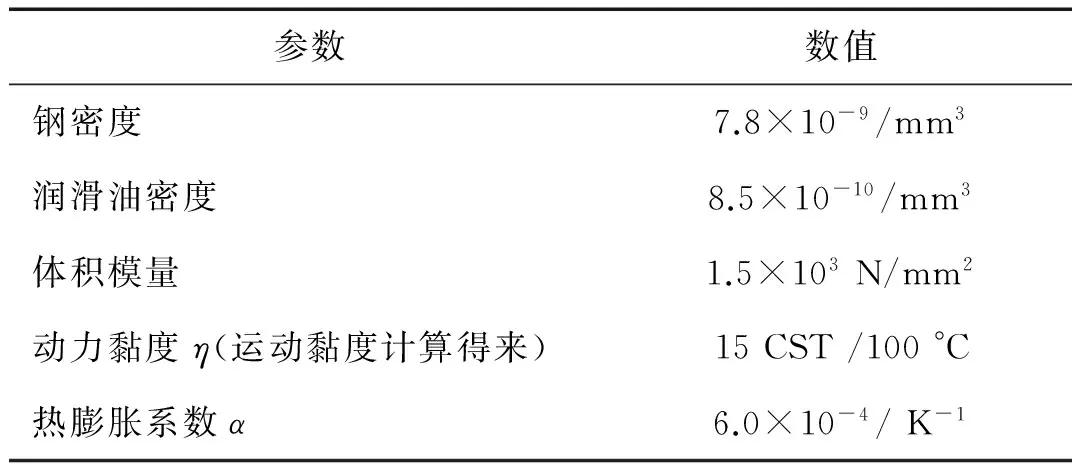
表2 材料计算参数

除上述材料参数外，还需使用材料的状态方程进行描述。选用 Mie-Gruneisen 方程，如下所示

p-ph=Γρ(Em-Eh)

(1)

(2)

Eh=(phη)/(2ρ0)

(3)

式中：p为液体压强；ph为Hugoniot压强；ρ0为液体初始密度；c0为液体声速；η为名义体积压缩应变,有η=1-ρ0/ρ,s为待定常数。Γ=Γ0(ρ0/ρ)为Gruneisen率，Γ0为材料常数,Em为单位质量内能。

1.2 有限元模型建立

建立的数值模型，如图4所示。油底壳划分为二阶四面体单元，C3D10M。欧拉立方体模型划分为八节点欧拉单元，EC3D8R。

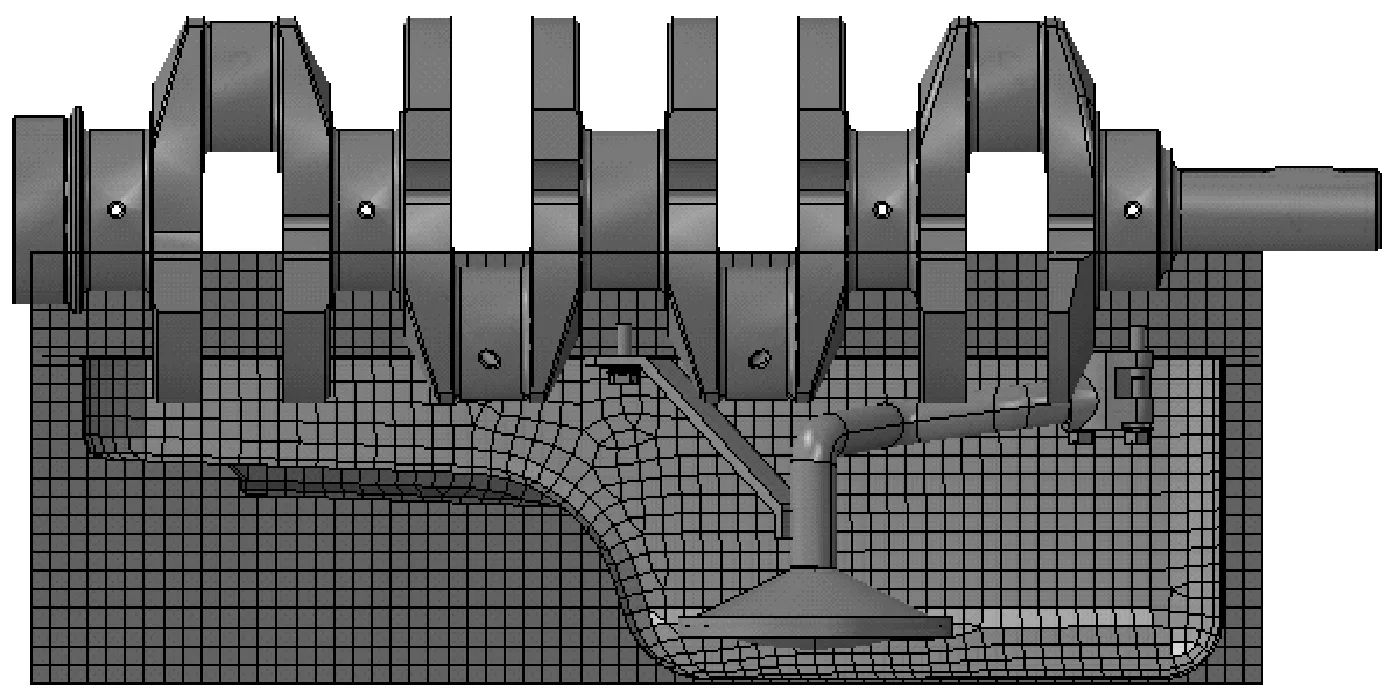
图4 在网格状态下的装配剖视图

在CEL算法中，欧拉材料通过欧拉体积分数(EVF)来跟踪其经过网格的状态，所有欧拉单元需通过指定值来代表其充满欧拉材料的比例。针对这样的问题，在初始条件里必须指定欧拉区域空间里面被流体材料所占据的初始体积。体积分数工具执行实体模型和欧拉网格的布尔运算。这将创建一组节点，定义了油底壳中的初始润滑油量状态，图5所示。拉格朗日材料和欧拉材料间的接触通过基于罚函数接触算法的一般接触分析来计算，当欧拉单元中体积分数0时，代表该欧拉单元中没有欧拉材料，拉格朗日单元能没有任何阻碍地通过欧拉单元。

1.3 计算工况

为获得对实际振荡情况的估计，又采用比较低的时间成本，采用时间缩放的计算策略，以减少计算时间，同样也是之所以选择双精度ABAQUS/Explicit执行计算的原因。表3为计算工况。

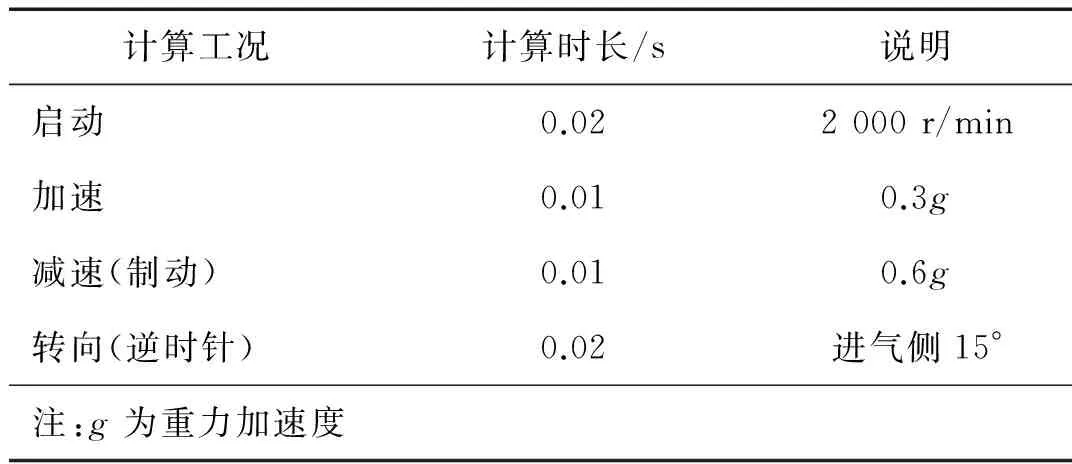
表3 数值模拟计算工况

2 计算结果与分析

2.1 启动工况计算结果分析

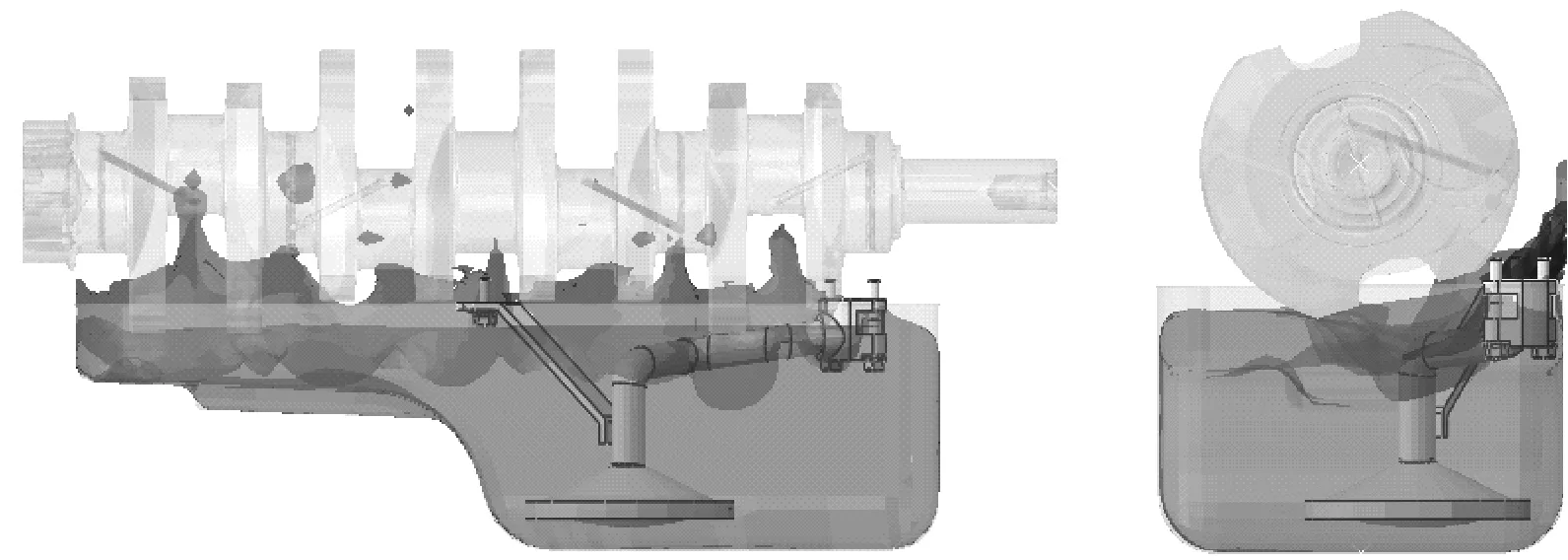
经过有限元计算分析，图6给出了采用CEL算法得到的润滑液在曲轴由静止到启动过程中润滑油的瞬时振荡过程，选取了其中几个典型时刻，可以看出，随着曲轴的转动，CEL算法可以清楚地计算得到润滑油随曲轴转动的运动情况，启动后随着曲轴转动，润滑油向一侧溅起，冲击油底壳一侧，并向整个曲轴-油底壳密封空间飞溅。

为进一步体现出CEL算法在流固耦合动态振荡过程可视化效果方面的优势，选取某一时刻，观测计算模型的材料流动情况和网格变化。如图7所示。

调取液面溅出网格一节点的体积分数变化曲线，如图8所示。可以看出该点的体积分数由1近似突变为0，再突变回1，正好验证了该处的润滑油由液体溅出再掉落回液体中的过程。

调取润滑油动能变化曲线，如图9所示。可以看出该润滑油的动能能量变化有许多尖峰，说明在振荡过程中润滑油有能量的波动，可以进行优化系统的NVH性能。

图10给出了基于材料体积分数加权平均的应力(SVAVG)分布。这种显示方式在多种材料混合时能更直观的显示不同液体材料的振荡情况。

(a) 时刻1

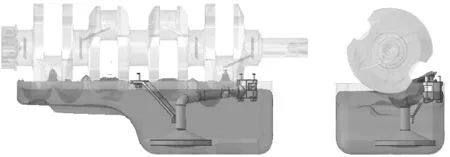
(b) 时刻2

(c) 时刻1

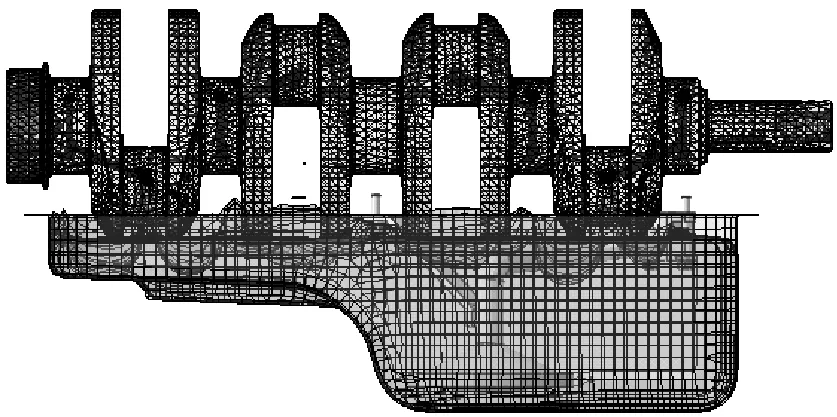
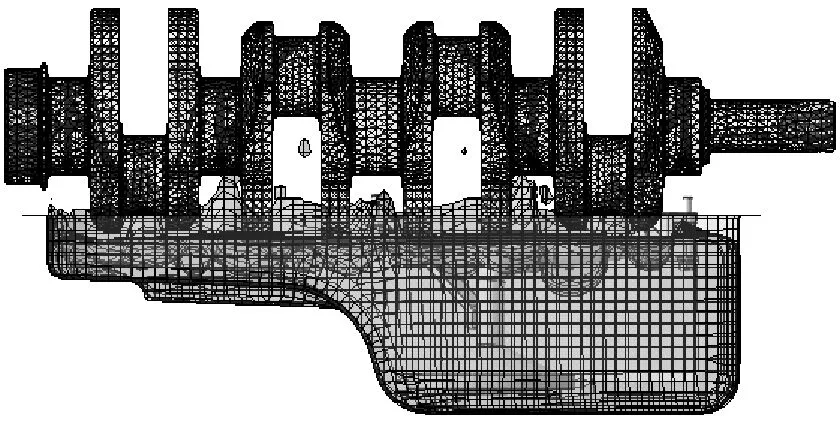
图8 关注点处体积分数变化情况

2.2 加速制动工况计算结果分析

图11是加速工况下计算时刻结束时润滑油的振荡情况及网格的变化情况，可以看出，当车辆突然加速时，由于油底壳的推动作用，润滑油会被推向前，但又由于惯性的作用，会导致润滑油在油底壳内来回晃动，由网格变化中的波纹可以看出，尾部波纹形状为两个凹峰，伴随着逐渐向前的传递波纹。

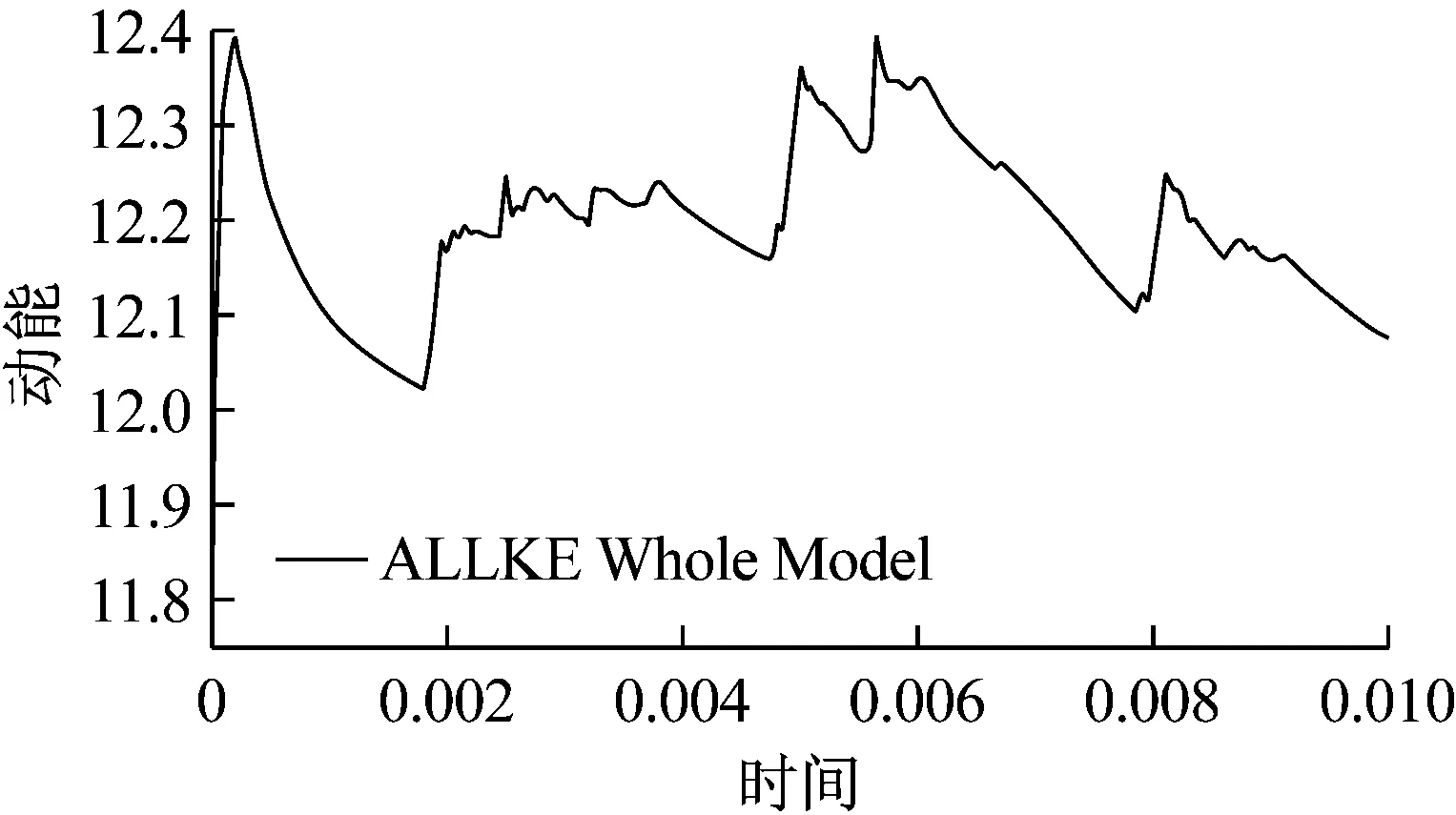
图9 系统动能变化情况

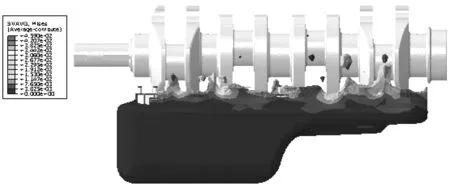
图10 加速工况计算结果

调取井槽尾部中间节点的应力变化情况，如图12所示，可以看出随着润滑油在油底壳内振荡，油底壳上的冲击应力也随之不断变化，出现多次尖峰，这对整机的NVH性能也有很大影响。

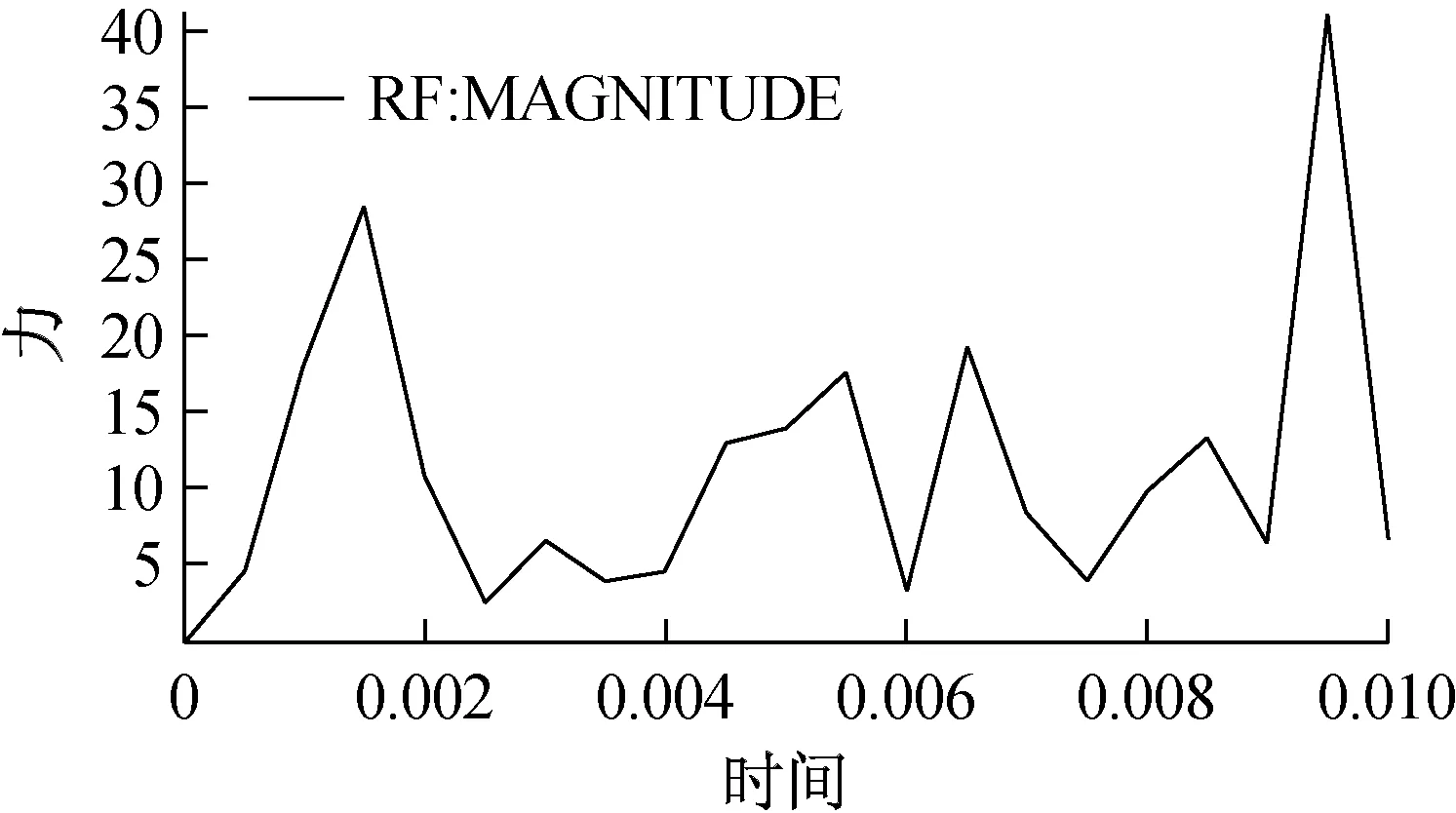
图12 井槽尾部中间区域节点应力变化曲线

图13是制动工况下计算时刻结束时润滑油的振荡情况及网格的变化情况，可以看出，当车辆突然制动时，由于油底壳的推动作用，润滑油会被推向前，但又由于惯性的作用，会导致润滑油在油底壳内来回晃动，由网格变化中的波纹可以看出，尾部波纹形状为两个凸峰，伴随着逐渐向前的传递波纹。

调取井槽尾部中间节点的应力变化情况，如图14所示，可以看出随着润滑油在油底壳内振荡，油底壳上的冲击应力也随之不断变化，出现多次尖峰，这对整机的NVH性能也有很大影响。

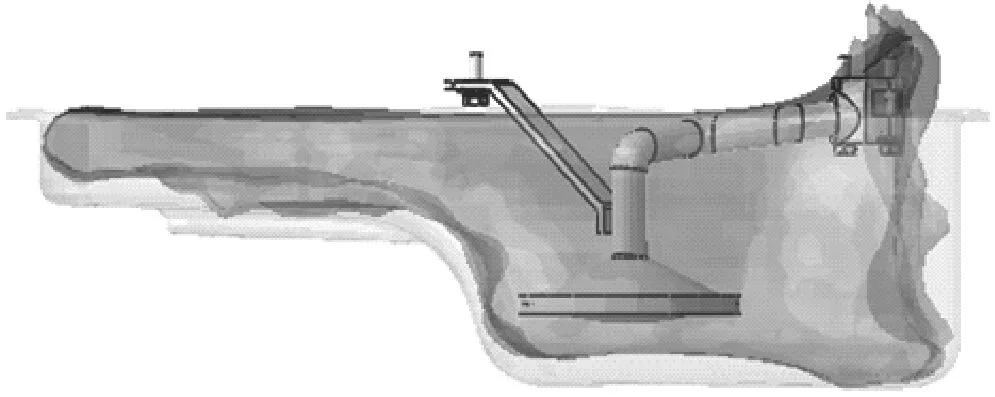
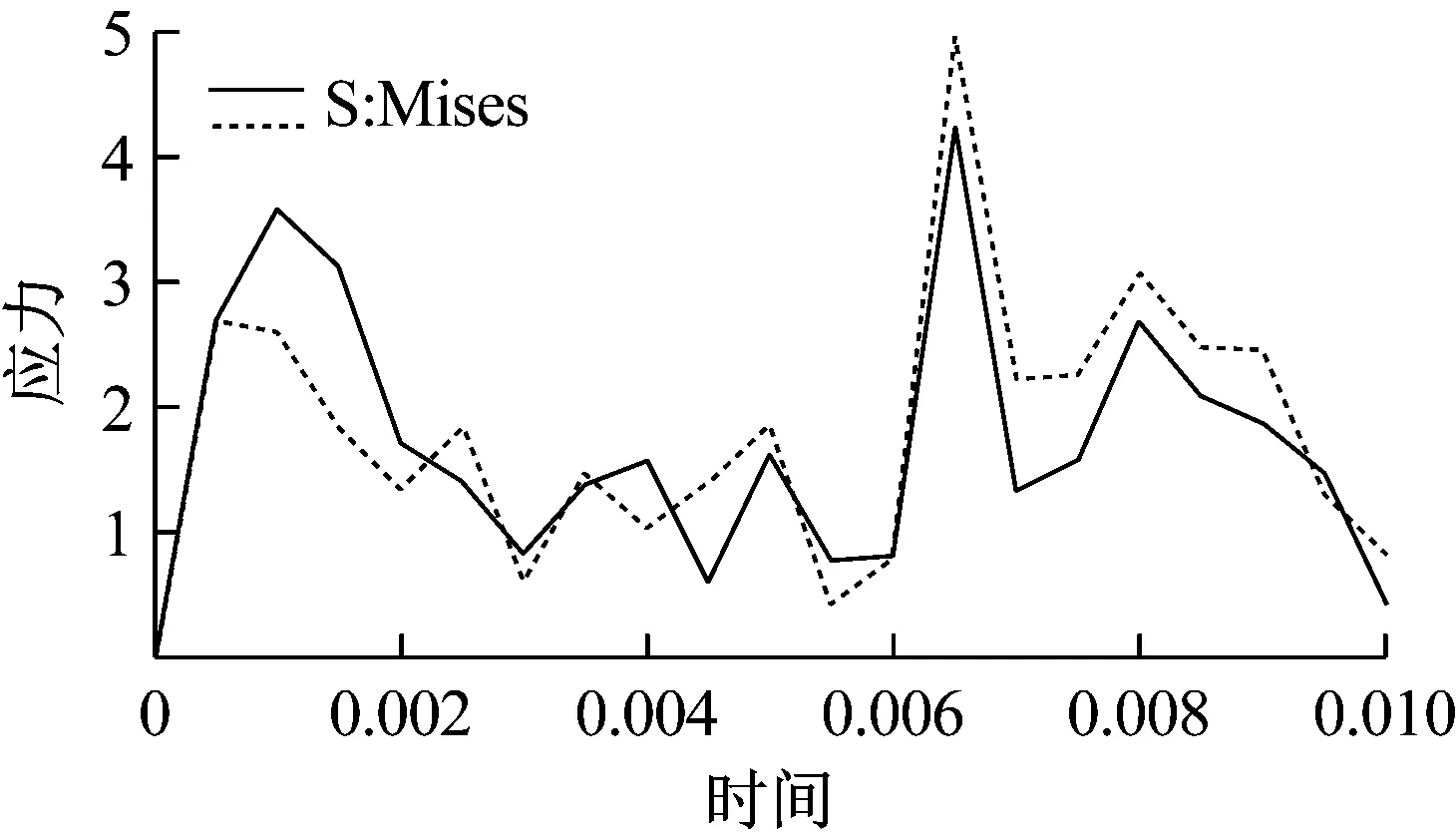
图14 井槽尾部中间区域节点应力变化曲线

2.3 转向工况计算结果分析

图15是加速工况下计算时刻结束时润滑油的振荡情况及网格的变化情况，可以看出，当车辆转弯时，由于油底壳的推动作用，润滑油会被推向前转弯方向，但又由于惯性的作用，会导致润滑油在油底壳内来回晃动，由网格变化中的波纹可以看出，波纹形状为向转向侧溅出，伴随着逐渐两侧传递波纹。

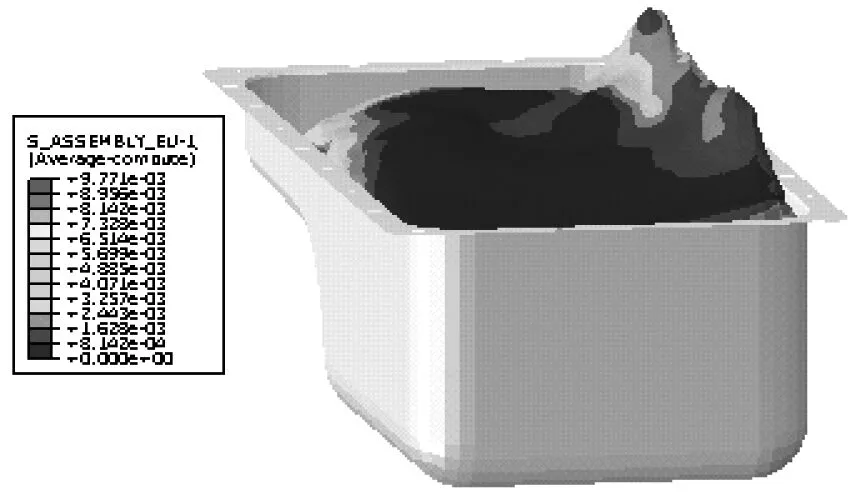
调取井槽一侧中部区域节点的应力变化情况，如图16所示，可以看出随着润滑油在油底壳内振荡，油底壳上的冲击应力也随之不断变化，出现尖峰，这是油底壳上一侧的节点调取结果。由这曲线尖刺可以看出，润滑液振荡这对油底壳以及整机的NVH性能也有很大影响。

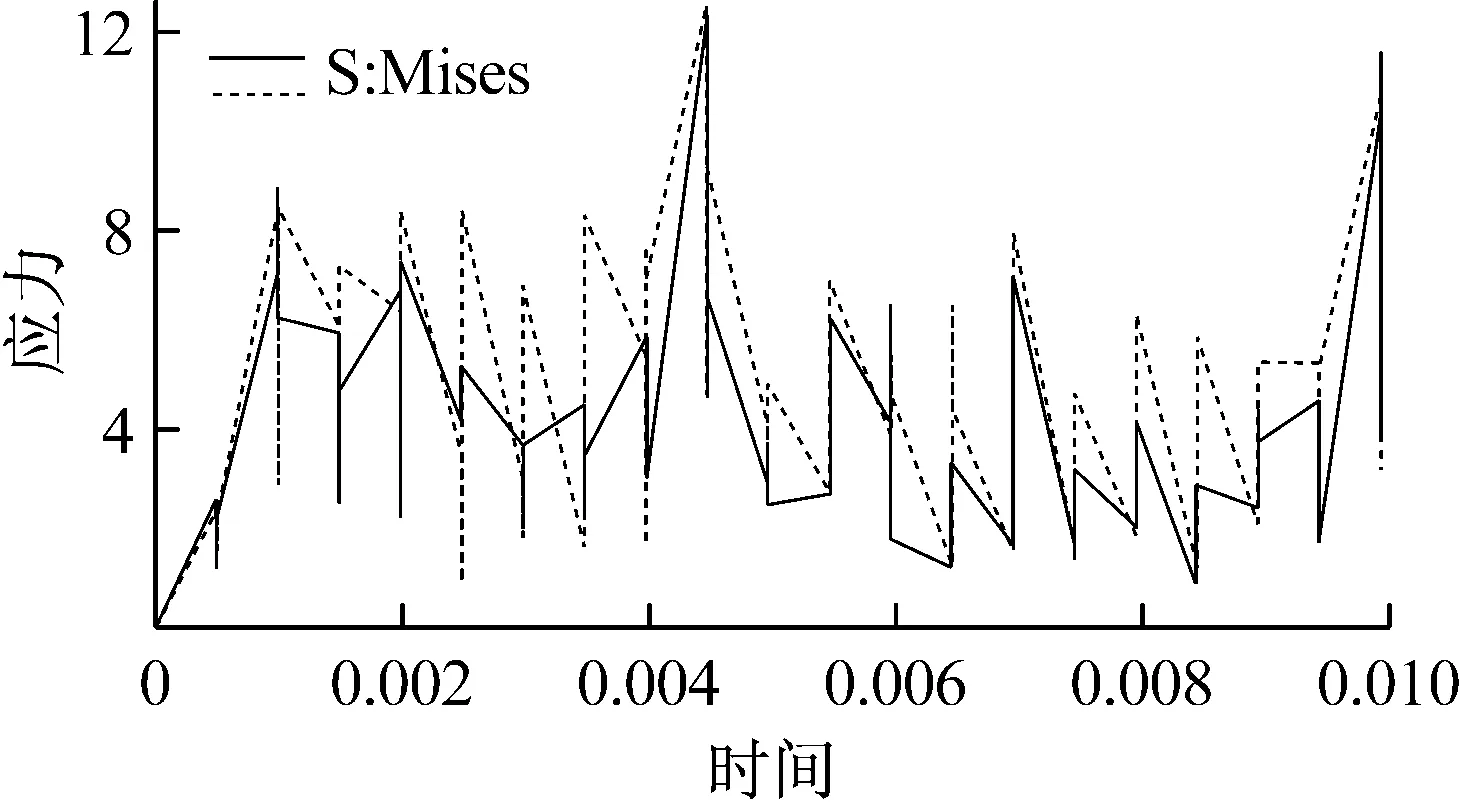
图16 油底壳一侧中间区域节点应力变化曲线

3 结 论

流固耦合振动问题一直以来是工程领域研究的热点和难点，它也是系统NVH性能分析上的一个不可缺少的研究环节，耦合的欧拉-拉格朗日算法(CEL算法)，在解决一些复杂的流固耦合问题方面具有强大的优势，可以较好地用于润滑油振荡问题的可视化模拟研究，文中建立了发动机曲轴-油底壳-润滑油流固耦合模型，采用CEL算法分析了润滑油在不同工况下的瞬态振荡情况，在加速减速制动等工况下，油底壳井槽后部区域受到了润滑油的不断的晃动和冲击，应力曲线也出现了多处尖峰；在转向工况下，油底壳侧面区域也受到了润滑油的不断的晃动和冲击，应力曲线也出现了多处尖峰，这对于发动机的NVH性能有很大影响；此外，CEL方法对于后续噪声的研究提供了新的思路，也为流固耦合振荡问题的数值分析探索了一个新的研究方法。

[1] 袁兆成. 内燃机设计[M].北京：机械工业出版社，2008.

[2] 陈佐一.流体激振[M].北京：清华大学出版社，1998.

[3] 徐文杰. 基于CEL算法的滑坡涌浪研究[J]. 工程地质学报,2012,20(3):350-354.

XU Wenjie. CEL algorithm study of reservoir surge induced by land slide [J]. Journal of Engineering Geology, 2012, 20(3):350-354.

[4] 魏鹏,史勇杰,徐国华. 复杂旋翼流场的耦合欧拉-拉格朗日数值方法[J]. 航空学报,2013,34(7):1538-1547.

WEI Peng, SHI Yongjie, XU Guohua. Coupled Eulerian-Lagrangian method for complicated rotor flow field prediction [J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(7): 1538-1547.

[5] NOH W F. CEL:A time-dependent two-space-dimensional coupled Eulerian-lagrangian code[C]∥Methods in Computational Physics, Volume 3,Fundamental Methods in Hydrodynamics. New York,NY: Academic Press, 1964:117-179.

[6] 王懿,贾旭,黄俊,等. 基于CEL的船舶抛锚入泥深度分析[J]. 石油机械,2014,42(12):44-47.

WANG Yi,JIA Xu,HUANG Jun,et al. Analysis of penetration depth of dropped anchor based on CEL [J].Chian Petroleum Machinery,2014,42(12):44-47.

[7] FOUCARD L, ARYAL A, DUDDU R, et al. A coupled Eulerian-Lagrangian extended finite element formulation for simulating large deformations in hyperelastic media with moving free boundaries[J]. Computer Methods in Applied Mechanics and Engineering, 2015, 283:280-302.

[8] ROSTAMI J, ABBASSI A. Conjugate heat transfer in a wavy microchannel using nanofluid by two-phase Eulerian-Lagrangian method[J]. Advanced Powder Technology, 2016, 27(1): 9-18.

[9] DIGGS A, BALACHANDAR S. Evaluation of methods for calculating volume fraction in Eulerian-Lagrangian multiphase flow simulations[J]. Journal of Computational Physics, 2016, 313: 775-798.

[10] BAHREMAND H, ABBASSI A, SAFFAR-AVVAL M. Experimental and numerical investigation of turbulent nanofluid flow in helically coiled tubes under constant wall heat flux using Eulerian-Lagrangian approach[J]. Powder Technology, 2015, 269: 93-100.

[11] VUJANOVI M, PETRANOVI Z, EDELBAUER W, et al. Modelling spray and combustion processes in diesel engine by using the coupled Eulerian-Eulerian and Eulerian-Lagrangian method[J]. Energy Conversion and Management, 2016,125:15-25.

[12] JARAUTA A, RYZHAKOV P, SECANELL M, et al. Numerical study of droplet dynamics in a polymer electrolyte fuel cell gas channel using an embedded Eulerian-Lagrangian approach[J]. Journal of Power Sources, 2016, 323: 201-212.

[13] 叶林征，祝锡晶，王建青，等.基于 CEL 不同角度超声空化微射流冲击的仿真分析[J].振动与冲击，2016,35(16):130-134.

YE Linzheng, ZHU Xijing, WANG Jianqing,et al.Simulations of ultrasonic cavitation micro-jet impact with different angles based on CEL [J]. Journal of Vibration and Shock, 2016,35(16):130-134.

[14] 卿启湘,杨会,刘杰,等. 基于CEL法的EPB切刀切削土体仿真分析[J]. 工程设计学报,2015,22(3):230-235.

QING Qixiang, YANG Hui, LIU Jie, et al. Simulation analysis on cutting soil for cutter of EPB based on CEL method [J]. Chinese Journal of Engineering Design, 2015, 22(3): 230-235.

[15] 姚小虎,黄愉太,欧智成,等. 基于CEL算法的水陆两栖飞机水上降落动力特性分析[J]. 华南理工大学学报(自然科学版),2015,43(6):110-115.

YAO Xiaohu, HUANG Yutai, OU Zhicheng, et al.CEL algorithm-based analysis of dynamics characteristics of amphibious aircraft landing on water [J]. Journal of South China University of Technology (Natural Science Edition), 2015, 43(6): 110-115.

[16] 王建华,兰斐. 钻井船插桩对邻近桩影响的耦合欧拉-拉格朗日有限元方法研究[J]. 岩土力学,2016,37(4):1127-1136.

WANG Jianhua, LAN Fei. A coupled Eulerian-Lagrangian FEMmethod for analyzing the effects of spudcan penetration on an adjacent pile [J]. Rock and Soil Mechanics, 2016, 37(4):1127-1136.