基于集总平均经验模态分解法(EEMD)的星箭解锁分离机构冲击响应分析

汪国元, 徐 洋, 胡晓楠， 盛晓伟， 蒋青飞

(1. 东华大学 机械工程学院, 上海 201620； 2. 北京卫星制造厂， 北京 102308)

航天器级间分离广泛采用了星箭解锁分离机构，它是卫星发射的关键部件。星箭解锁分离机构分为火工分离和非火工分离两种方式，目前我国大部分分离装置都采用火工分离装置。火工分离装置结构简单，但解锁分离时会产生很大的冲击载荷，不利于火箭卫星的顺利发射[1]。火工分离装置由最初的点式分离装置发展到目前主流的包带式，国内很多专家学者对此做了大量相关研究，如Li等[2-3]对包带式分离装置的动力学特性及故障分析等方面的研究；包带式相比传统点式具有应用成熟、可靠性高、分离冲击相对较小等优点[4]，但依旧有附加污染明显、不可重复利用等缺点。未来分离装置的发展方向是非火工，记忆合金型星箭解锁分离机构作为一种甚低冲击的新型点式非火工分离装置[5]，其稳定性高，解锁分离迅速，产生的冲击也非常小；但国内在应用方面还不太成熟，需要投入更多研究；对其解锁分离过程产生的冲击响应进行分析，为星箭解锁分离机构的可靠性、安全性设计提供参考很有必要。经验模态分解法(EMD)是由Huang[6]提出，EMD几乎能对所有非平稳信号进行平稳化处理，将非平稳信号按不同尺度逐级展开，分解成具有不同物理意义的本征模态函数IMF和表征信号整体变化趋势的残余分量。EEMD在EMD的基础上添加高斯白噪声,在很大程度上抑制了模态混叠的问题，提高了分解得到不同IMF的准确性[7]。对IMF和残余分量的分析可以更深入的了解原始信号中所包含的成分和特征，基于EEMD，本文对记忆合金型星箭解锁分离机构解锁分离过程中产生的冲击响应信号进行了详细分析。

1 集总平均经验模态分解法(EEMD)

1.1 经验模态分解法(EMD)原理

EMD可以根据信号的自身局部特征，逐级分解成独立的IMF和残余分量。而每阶IMF都应该满足如下要求：① IMF中的零点和极点个数相差不能超过1,即整个IMF的零极点个数相等或相差1；② 由极大值组成的上包络线和极小值组成的下包络线的平均值为零。

EMD的具体分解方法为：

(1) 设原始信号为y(t)，用三次样条曲线分别将极大值和极小值点连接起来，作为y(t)的上下包络线；然后计算上下包络线的平均值，用曲线m1(t)表示，如图1所示；再用原始信号减去上下包络线平均值，即

f1(t)=y(t)-m1(t)

(1)

图1 原始信号、上下包络线及均值曲线

(2) 判断f1(t)是否满足IMF应有的两个条件，若不满足，对f1(t)重复步骤1，直到得到第一阶模态分量IMF1，具体如图2所示。

图2 EMD分解得到第一阶模态分量

经过k次重复，直到符合要求，得到的f1k(t)则成为第一阶IMF1，即

c1(t)=f1k(t)

(2)

(3) 用原始信号y(t)减去c1(t)，得到第一阶残余分量RES,记作r1(t)：

y(t)-c1(t)=r1(t)

(3)

由于r1(t)中仍含有很多不同频率分量，需要对r1(t)进行再次分解。经过逐级分解，可依次得到剩下的IMF2、IMF3、…、IMFn，即

(4)

以上分解结束的条件是rn(t)是一个单调函数，最终可分解得到

(5)

由式(5)可以看出：原始信号y(t)可分解为一系列固有模态函数cn(t)和残余分量rn(t)。EMD已经被应用于很多领域，但仍存在一些待解决的问题，比较突出的是容易产生模态混叠，而EEMD则比较好的解决了这个问题。

1.2 集总平均经验模态分解法(EEMD)原理

EEMD算法的核心是EMD，但相对于EMD分解效果更好，比较好的解决了模态混叠的问题。黃鍔(N E Huang)和Flandrin等通过对白噪声的分解统计发现，用EMD分解高斯白噪声时，白噪声中的频率成分被规律的分解开来；鉴于此，黃鍔将白噪声添加到需要分解的原始信号中用来补充一些缺失的成分，从而达到比较好的分解结果。EEMD的具体分解过程如图3所示，图3中最后结果ai便是EEMD分解原始信号y(t)得到的各阶模态分量IMFs。此算法利用了相关性和峭度的门限值设定，实现了EMD的消噪目的[8]。

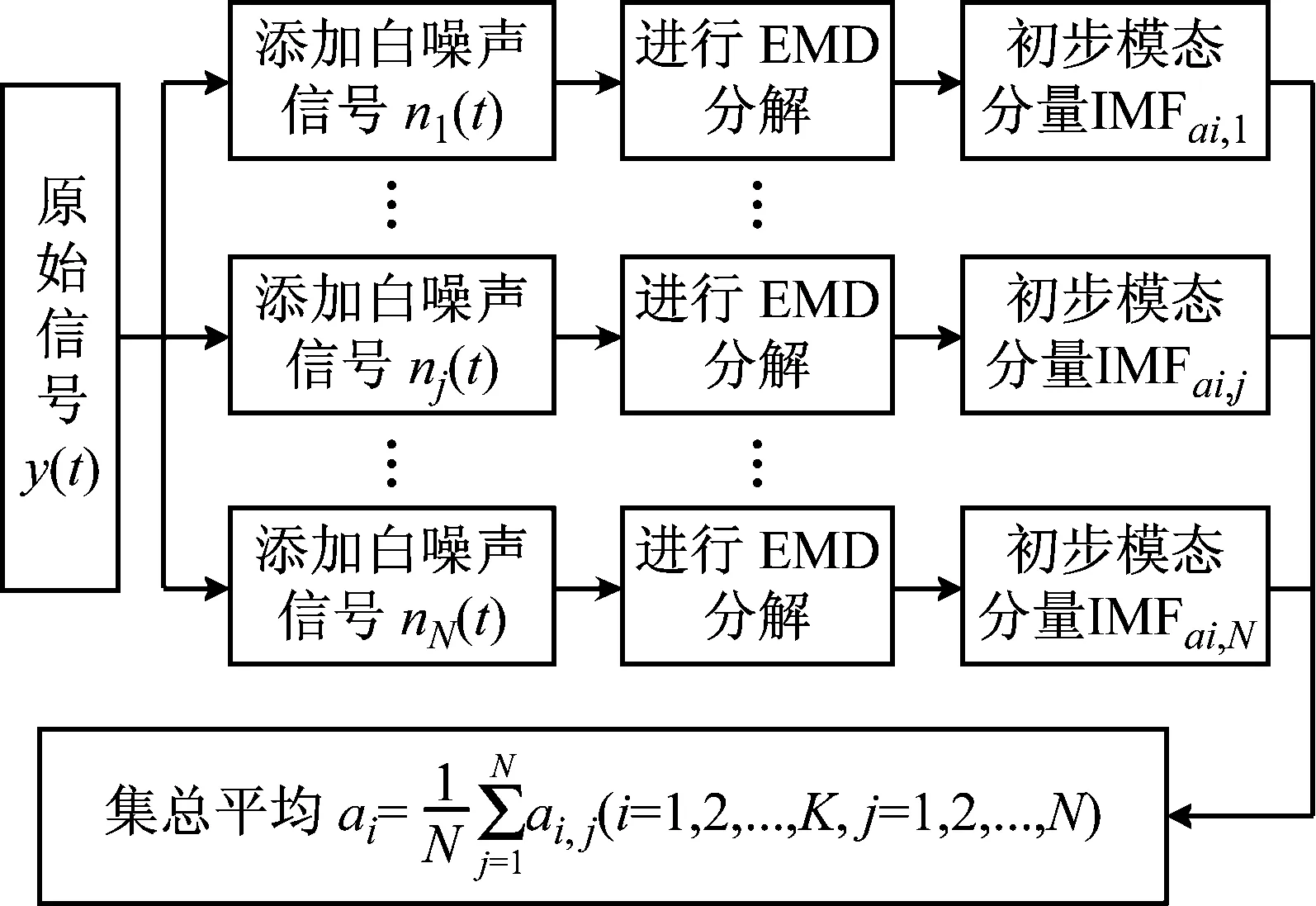
图3 EEMD分解过程

对于EMD和EEMD在冲击信号分析方面的研究，目前以对冲击信号的特征提取和去噪为主。张春棋等[9]对爆炸冲击信号进行EMD分解，并结合时频分析，精确反应了爆炸冲击信号的特征；孔佑炳等[10]结合EEMD，实现对剥落故障混合陶瓷球轴承振动信号双冲击特征的有效分离提取。基于已有研究，再结合EEMD，可将星箭解锁分离机构分离时产生的原始冲击信号按高低频逐级分解开来[11]，以便更加深入研究冲击信号成分。

2 基于EEMD的星箭解锁分离机构冲击响应分析

2.1 记忆合金型星箭解锁分离机构

记忆合金型星箭解锁分离机构如图4所示，该机构由形状记忆合金(Shape Memory Alloy, SMA)驱动，主要用于点式分离。当收到上级供电后，控制组件将电能转变为热能，由于SMA具有应变储能特性，当达到SMA的相变温度时，SMA产生回复应力和应变[12]，带动触发轴转动，解除对一级摆臂限位，继而二级摆臂限位解除，从而解除主承力螺母限位。过程中预紧载荷逐级释放，由于主承力螺母与承力螺杆间为非自锁梯形螺纹连接，主承力螺母的转动势能释放并转变为承力螺杆的直线运动动能，承力螺杆最终脱离连接界面，星箭实现解锁分离。该机构解锁分离过程中会产生三次冲击响应，基于EEMD可将三次冲击响应信号按高低频率逐级分解开来，对不同频段进行分析。

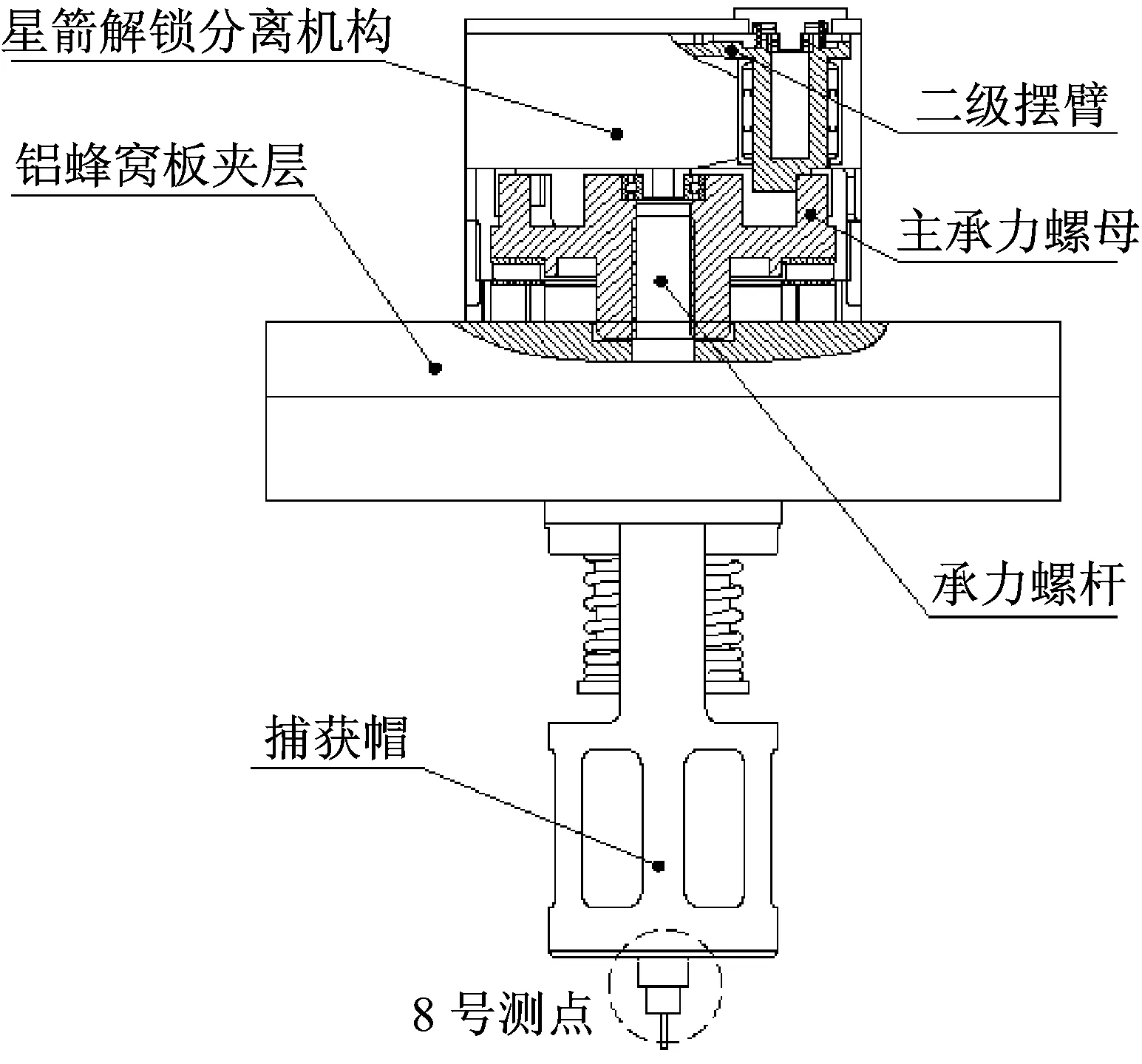
图4 星箭解锁分离机构简图及测点布置图

用数据采集系统采集星箭解锁分离机构解锁分离过程的冲击信号，测点布置如图4所示，采用对称布局；并对星箭解锁分离机构进行模态实验，现场实验如图5所示，得到该机构的前几阶模态。

由于测点的对称性，以及振动传递过程为由近到远，可选取蜂窝板上1、4点代表星箭解锁分离机构解锁过程铝蜂窝板的振动特性，根据测得数据分析可知1、4、8产生的冲击响应均在8.5～9 s时间内，为减少计算量，此3点的后续分析数据均取于8.5～9 s内。图6为1、4号测点和8号测点的冲击信号，可知其幅值大小为400 m/s2,即产生的加速度为约40 g；谭雪峰等[13]通过一种简化的轴对称圆环振动模型模拟了包带式火工分离装置，分析发现分离时产生的瞬时加速度可达2 500 g，对比可知该分离装置分离时产生的冲击载荷要比火工分离装置小接近两个数量级。

图5 现场实验图

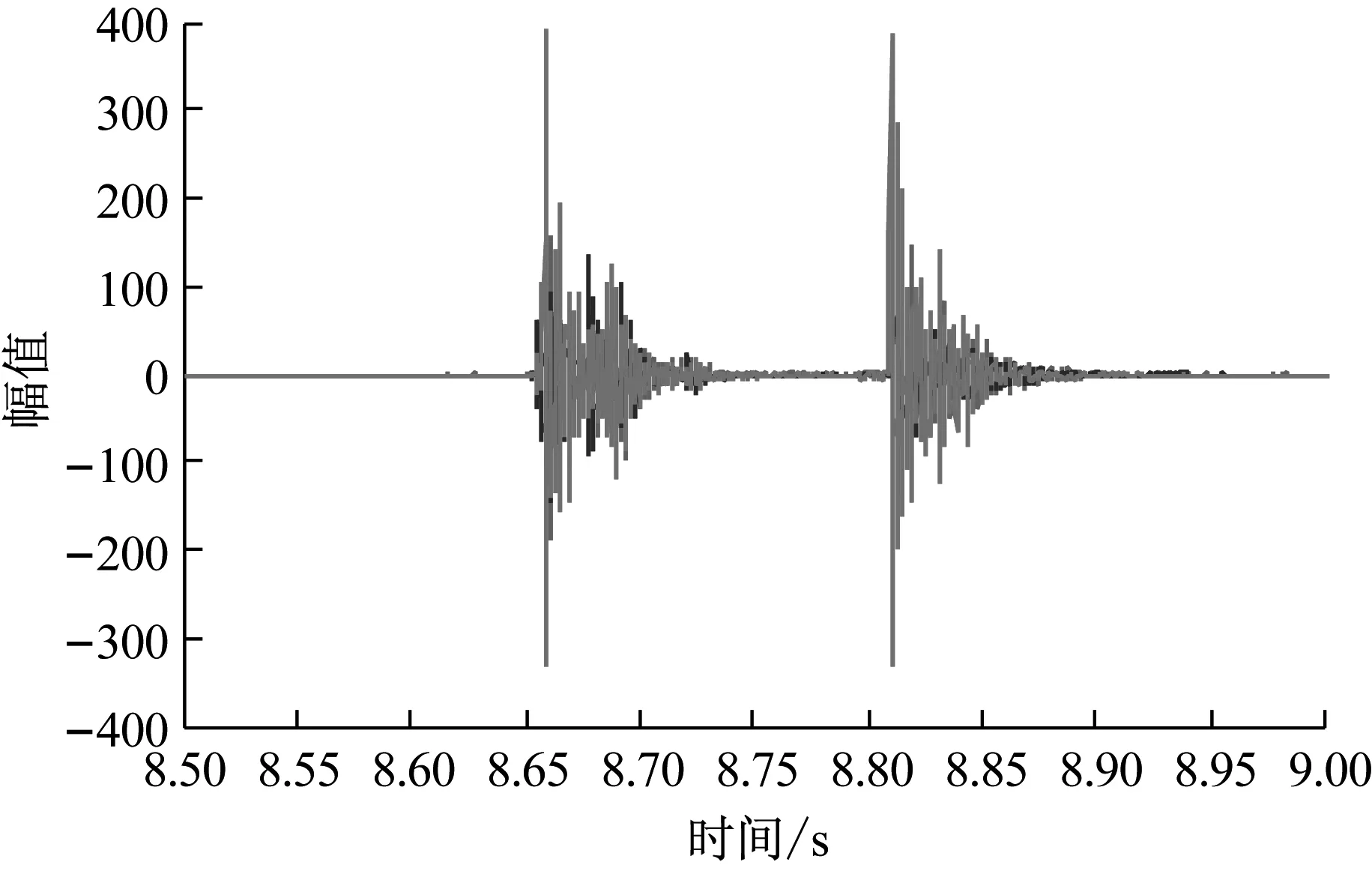
图6 1、4、8号测点冲击响应信号

2.2 基于EEMD的星箭解锁分离机构冲击响应分析

对1号测点的冲击响应信号进行EEMD分解，如图7所示。

图中第一个信号为原始信号，后面依次为模态分量IMF1～IMF7，最后一个为分解后的余项RES，RES是一个幅值变化很小的序列，表征了1号测点处铝蜂窝板冲击振动的整体趋势。从EEMD的分解结果可知：

(1) 模态分量IMF1到IMF3是冲击信号中分解出的频率最高、波长最短的波动，这代表信中的噪声和高频；

(2) IMF1振幅最大，最大振幅接近200 m/s2，表明其所占能量很大，IMF2和IMF3振幅也接近50 m/s2，占了一定比例的能量；

(3) 再依次往下分解出各分量IMF4-IMF7，可以看出变化趋势为，随着分解的进行，所得各分量频率逐渐变低、波长越来越长，直到分解出频率已经很低的最后一个分量。

以上表明冲击信号中同时包含了高频成分和低频成分，其中低频成分是冲击载荷激起的局部振动的固有频率，而高频成分则是由于冲击所致。再进一步对

IMF分量的频谱图进行分析，1号测点各IMF对应频谱图如图8所示，其中箭头指示为各IMF分量对应的主要频率；前4阶IMF(IMF1～IMF4)的时频图如图9(a)～9(d)所示，可以比较清楚的看到各频段产生的时间及频率成分。

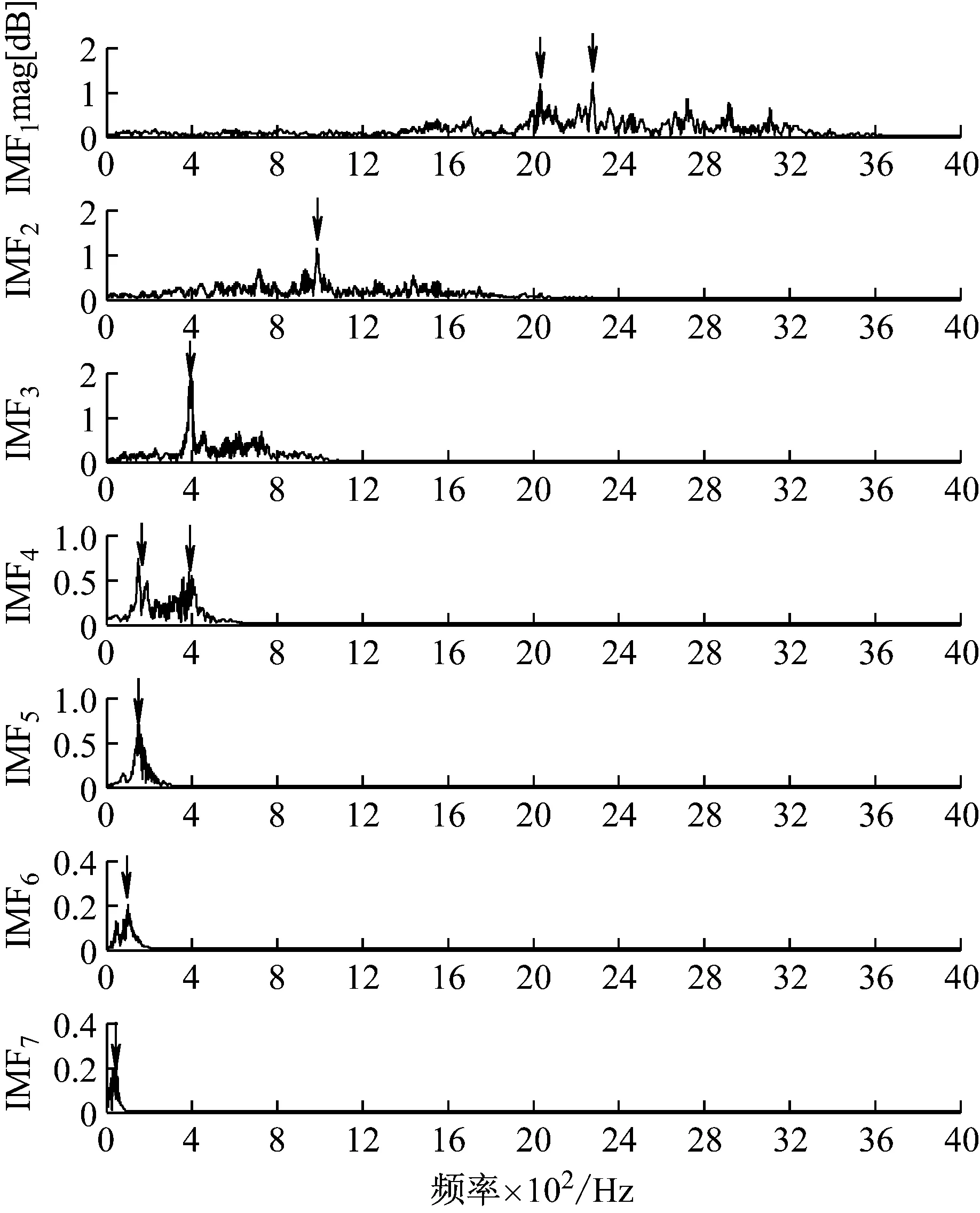
图8 1号测点各IMF对应频谱图

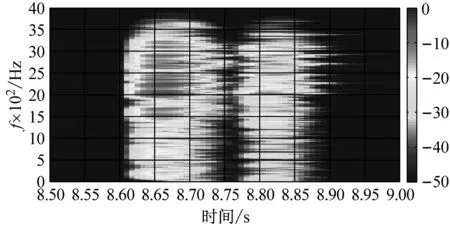
(a) 1号测点对应IMF1时频图

(b) 1号测点对应IMF2时频图

(c) 1号测点对应IMF3时频图

(d) 1号测点对应IMF4时频图

从1号测点IMFS的频谱图和时频图可以看出：IMF1～IMF7为不同阶高频到低频的模态分量,IMF1包含 频率成份最宽，而且大多是高频振动，IMF2～IMF7频率慢慢降低，形成从高频到低频的不同模态分量。1号点IMFS模态分量对应的频率与模态实验结果对比具体如表1所示，结合时频图和表1分析可知：

(1) 由时频图可知，解锁分离过程要小于0.15 s；

(2) IMF1包含频率成分最宽，而且大多是高频振动，比较显著的有2 050 Hz和2 250 Hz，这主要是由于冲击造成的高频振动；

(3) IMF2中幅值比较大的频率有720 Hz和1 000 Hz，与模态实验结果中的4、6阶模态有一定的吻合，IMF3对应的400 Hz也与模态实验结果的1阶模态相吻合；

(4) IMF4有200 Hz、400 Hz两种模态，再之后 IMF5～IMF7是一些局部的低频振动，从低到高有180 Hz、100 Hz、40 Hz，这说明星箭解锁分离机构中的某些部件的固有频率可能是这些，在相关结构设计时，要尽量避开这几阶模态。

表1 模态实验结果与1号测点各IMF分量频率对比

从EEMD分析结果可以看到有些低频成分在模态实验中没有出现，这主要是因为模态实验为测全局的模态，以整体模态考虑，而IMF模态分量可以反映到局部，这也可以补充实验的不足。

用同样的方法再分析4号测点各IMF，发现与1号测点振动情况非常接近，主要区别是4号点振动幅值的峰值要稍小。根据振动传递原理[14]以及测点布置图可知，冲击振动是从1号点传递至4号点，这符合振动实际情况，也间接说明了铝蜂窝板的减震效果比较理想。

8号测点与1、4号测点的情况有些不同：8号测点在捕获帽上，是星箭解锁分离机构解锁后直接冲击部位，而1、4号测点是传递至蜂窝板的冲击振动情况，对比可知蜂窝板的振幅要明显小于星箭解锁分离机构本身，说明铝蜂窝板减振效果良好。取8号点测试数据进行EEMD分解，分解结果与1、4号测点结果类似，冲击信号中同时包含了高频成分和低频成分。不同的是，8号点的第三次冲击的模态分量幅值要明显大于前2次的冲击，表明捕获帽受到第三次的冲击要大于前两次，这也说明捕获帽顶部应有必要的减振措施。另外，对比前两次冲击，第三次冲击幅值也在可接受范围，没有特别大差异，这说明减振帽处的减震片减振效果比较理想。

最后综合所有测点冲击信号的EEMD分解结果以及模态实验结果，发现前两阶模态分量IMF主要为冲击引起的高频振动，部分IMF2和IMF3、IMF4为冲击激励引起的不同阶固有模态振动，而IMF5之后为局部振动。

3 结 论

基于EEMD算法，详细分析了记忆合金型星箭解锁分离机构解锁分离过程中受到的冲击响应情况，通过分析铝蜂窝板和星箭解锁分离机构本身，得出如下结论：

(1) 该机构解锁分离迅速稳定，小于0.15 s； 捕获帽处的减振片减振效果理想；蜂窝板的振幅要明显小于星箭解锁分离机构本身，这和铝蜂窝板具有减振作用有关。

(2) 对不同测点的冲击响应信号进行集总平均经验模态分解(EEMD)后，得到不同测点模态分量，它们有共同规律：分解后的各分量IMF包含了不同的时间特征尺度，并以不同的分辨率显示信号特征；在分量中，第一个分量IMF1所占的冲击比重相当大，甚至是最大的一部分，它是原始冲击信号中分解出的频率最高、波长最短的波动；从IMF2到 IMF7，可以看出随着分解的进行，所得各分量频率逐渐变低、波长越来越长，直到分解出最后一个表征冲击振动整体趋势的分量RES。

(3) EEMD分解后各IMF中除了冲击响应引起的高频振动外，还包含不同阶固有模态的中频成分，且和模态实验结果相吻合；这表明，该机构解锁分离过程中，除了受冲击引起的高频振动，还会激起该机构的多阶模态振动，在相关设计时要避免该频率部分。

[1] 张欢，刘天雄，李长江，等. 航天器火工冲击环境防护技术现状与应用[J]. 航天器工程，2014, 23(2): 104-113.

ZHANG Huan, LIU Tianxiong, LI Changjiang,et al. Status and application analysis of spacecraft pyroshock protection techniques [J]. Spacecraft Engineering, 2014, 23(2): 104-113.

[2] LI J, YAN S, TAN X. Dynamic-envelope analysis of clamp-band joint considering pyroshock of satellite separation[J]. Journal of Spacecraft and Rockets, 2014, 51(5):1390-1400.

[3] 谭雪峰，阎绍泽. 包带式星箭连接结构动力学模拟及故障分析[J]. 清华大学学报，2010, 50(8):1205-1209.

TAN Xuefeng,YAN Shaoze. Dynamic simulations and failure analysis of a clamp band system for spacecraft[J]. J Tsinghua Univ(Sci&Tech), 2010, 50(8): 1205-1209.

[4] 谭雪峰，阎绍泽. 星箭包带式连接结构动力学研究进展[J].导弹与航天运载技术, 2010(1): 1-6.

TAN Xuefeng，YAN Shaoze. Evolution of research on dynamics of clamp band system between satellite and launch vehicle [J]. Missiles and Space Vehicles, 2010(1): 1-6.

[5] 白志富，果琳丽，陈岱松. 新型非火工星箭连接分离技术[J]. 导弹与航天运载技术，2009(1): 31-37.

BAI Zhifu, GUO linli, CHEN Daisong. Late-model non-pyrotechnic devices for separation of satellite-launching vehicle [J]. Missile and Space Vehcile, 2009(1): 31-37.

[6] HUANG N E．The empirical mode decomposition and the Hilbert spectrum for nonlinear and non stationary-time series analysis[J]. Proceedings of the Royal Society A，1998，454(1971): 903-995．

[7] WU Z H, HUANG N E． Ensemble empirical mode decomposition: a noise assisted data analysis method [J]. Advances in Adaptive Data Analysis, 2009, 1(1): 1-41.

[8] 苏文胜，王奉涛，张志新，等. EMD降噪和谱峭度法在滚动轴承早期故障诊断中的应用[J]. 振动与冲击, 2010, 29(3): 18-21.

SU Wensheng, WANG Fengtao, ZHANG Zhixin, et al. Application of EMD denoising and spectral kurtosis in early fault diagnosis of rolling element bearings [J]. Journal of Vibration and Shock, 2010, 29(3): 18-21.

[9] 张春棋，贾云飞，康金. 基于HHT的爆炸冲击波信号分布特性测试分析[J]. 测试技术学报, 2015, 29(6): 473-477.

ZHANG Chunqi, JIA Yunfei, KANG Jin. Explosive blast test and distribution analysis based on HHT [J]. Journal of Test and Measurement Technology, 2015, 29(6): 473-477.

[10] 孔佑炳, 郭瑜，伍星. 基于EEMD的混合陶瓷球轴承故障双冲击特征提取[J]. 振动与冲击, 2016, 35(1): 17-22.

KONG Youbing, GUO Yu, WU Xing. Double-impulse feature extraction of faulty hybrid ceramic ball bearings based on EEMD [J]. Journal of Vibration and Shock, 2016, 35(1):17-22.

[11] 姚熊亮, 张阿漫. 经验模态分解方法在结构冲击信号分析中的应用[J]. 中国舰船研究, 2006,4(1): 11-15.

YAO Xiongliang, ZHANG Aman. Application of EMD method in the analysis of structural impulse signals [J]. Chinese Journal of Ship Research, 2006,4(1):11-15.

[12] 闫晓军, 张小勇, 聂景旭，等. 采用SMA驱动的小型空间磁悬浮飞轮锁紧机构[J]. 北京航空航天大学学报, 2011, 37(2): 127-131.

YAN Xiaojun, ZHANG Xiaoyong, NIE Jingxu, et al. Prototape SMA actuated locking device for small space magnetic bearing flywheels [J]. Journal of Beijing University of Aeronautics and Astronautics, 2011, 37(2): 127-131.

[13] 谭雪峰，阎绍泽. 星箭分离面径向冲击预示的简化圆环分析方法[J]. 机械工程学报，2010, 46(16): 95-100.

TAN Xuefeng, YAN Shaoze. Simplified analytical method of radial shock response of satellite-rocket separation interface[J]. Journal of Mechanical Engineering, 2010, 46(16): 95-100.

[14] 褚怀保，叶红宇，杨小林,等. 基于损伤累积的爆破振动传播规律试验研究[J]. 振动与冲击, 2016, 35(2): 173-177.

CHU Huaibao, YE Hongyu, YANG Xiaolin, et al. Experiments on propagation of blasting vibration based on damage accumulation [J]. Journal of Vibration and Shock, 2016, 35(2): 173-177.