计及附加质量系数变化效应的立管涡激振动时域响应研究

袁昱超， 薛鸿祥， 唐文勇

(1. 上海交通大学 海洋工程国家重点实验室， 上海 200240;2. 高新船舶与深海开发装备协同创新中心， 上海 200240)

随着对于石油及天然气的开采逐渐延伸向深海领域，作为海上油气勘探和生产系统重要组成部分，深海立管的涡激振动问题越发引起学术界及工程界的广泛关注。当海流流经具有圆形截面的立管时，立管表面会发生周期性的漩涡脱落现象，漩涡脱落致使立管周围流场改变，产生漩涡力，进而引发立管振动，即涡激振动(Vortex-Induced Vibration，VIV)。若立管响应频率与涡脱频率相近，涡激振动幅值将会明显增大，称为“锁定”，“锁定”现象的存在易使立管造成严重的疲劳损伤。

对于细长结构物涡激振动的预报，现有数值模型总体上可分为频域和时域两类方法。基于半经验模型的频域预报工具，如SHEAR7[1]和VIVANA[2]，已发展得较为成熟，但频率方法无法考虑非定常流工况以及浮体、海床等复杂边界条件效应。因此，越来越多的学者致力于涡激振动时域预报方法研究。时域方法根据其依托的核心算法可分为两类：尾流振子法和半经验模型法。尾流振子法采用Vander Pol振子模型描述流场，但受控参数较多，找到一套通用的控制参数同时满足自激振动和受迫振动试验结果存在一定的难度。

早期的基于半经验模型的时域预报方法以ABAVIV[3]和SimVIV[4]为代表。近年来，Wang 等[5-7]基于受迫振动试验数据也相继开发了海洋立管时域预报模型，验证了半经验模型法解决涡激振动问题的可行性。但上述时域预报方法一般将涡激振动系统的附加质量系数假定为常数，取1.0。事实上，在整个时间历程内，附加质量系数会因为立管响应频率和振动幅值的改变而发生变化，近年来开展的模型试验研究[8]表明涡激振动过程中附加质量系数真实值普遍不等于1.0。相较均匀流工况，非均匀流条件下立管涡激振动过程中的附加质量系数分布更加复杂。附加质量系数的改变直接导致结构湿模态的预报产生偏差，影响涡激振动主导频率计算精度，并进一步影响激励力、阻尼力以及惯性力的计算。因此，为了得到更为准确的预报结果，附加质量系数变化效应对涡激振动的影响应在模型中予以考虑。

本文提出了一套可供选择的基于半经验模型的时域预报方法，用以分析海洋立管计及附加质量系数变化效应的涡激振动响应。该数值模型引入附加质量单元，可以有效地模拟结构物与流体相互作用过程中立管固有频率、主导频率、激励力、阻尼力以及附加质量力等随附加质量系数的改变如何变化。基于提出的时域方法，本文对某7.9 m试验立管在均匀流下以及某90 m试验立管在线性剪切流下的涡激振动进行了预报，并将预报结果与试验结果进行了对比，论证了本文模型的可行性及准确性。

1 涡激振动响应分析模型

由于海洋立管通常具有较大的细长比，立管模型可认为是服从Euler-Bernoulli梁模型假定的抗弯弹性结构，立管在横流方向的运动控制微分方程由式(1)表示，本文选取Cartesian坐标系，x轴为顺应流速方向，y轴为与流速垂直的横向，z轴为竖直向上方向

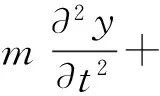
Fy(A*,fr)

(1)

式中：m为立管单位长度质量；c为阻尼系数，包括结构阻尼及水动力阻尼；E为弹性模量；I为惯性矩；T为有效张力；A*为无因次幅值；fr为无因次频率，fr=f·D/V；f为响应频率，Fy为水动力载荷。

水动力载荷Fy由与立管速度同相位的激励力FV和与立管加速度同相位的惯性力FM两部分组成。上述两个水动力力成分均由立管响应频率、振动幅值以及流速共同决定。本文假定作用于立管单元的激励力在一个周期内服从正弦规律变化，水动力载荷可表示为

(2)

式中：CV为激励力系数；ω为响应频率对应的圆频率；ρf为流体密度；Ca为附加质量系数；V为流速；D为立管直径。

1.1 激励力及阻尼模型

Gopalkrishnan开展了一系列圆柱体单自由度受迫振动试验研究，获取的激励力系数云图如图1所示。图中粗实线标注出激励力系数为零的边界，此边界是判定涡激振动是否发生的关键指标。本文在激励力系数云图的基础上，对无因次频率及无因次幅值进行插值获得需要的激励力系数CV。试验中对应的Strouhal数为0.193。

本文阻尼模型由结构阻尼和水动力阻尼两部分构成。当激励力系数大于零时，激励力与立管速度同向，整个系统内能量由流体传入立管，而当激励力系数小于零时，水动力阻尼力作用于立管，能量也将由立管传回流体。本文假定流体传入立管的等效能量在一个振动周期内传回流体，根据能量守恒原理，水动力阻尼系数可通过式(3)计算得到

(3)

当无因次频率超出图1试验数据范围时，认为激励力转变给水动力阻尼，本文采用由Venugopal[9]针对涡激振动提出的经验阻尼模型模拟水动力阻尼。

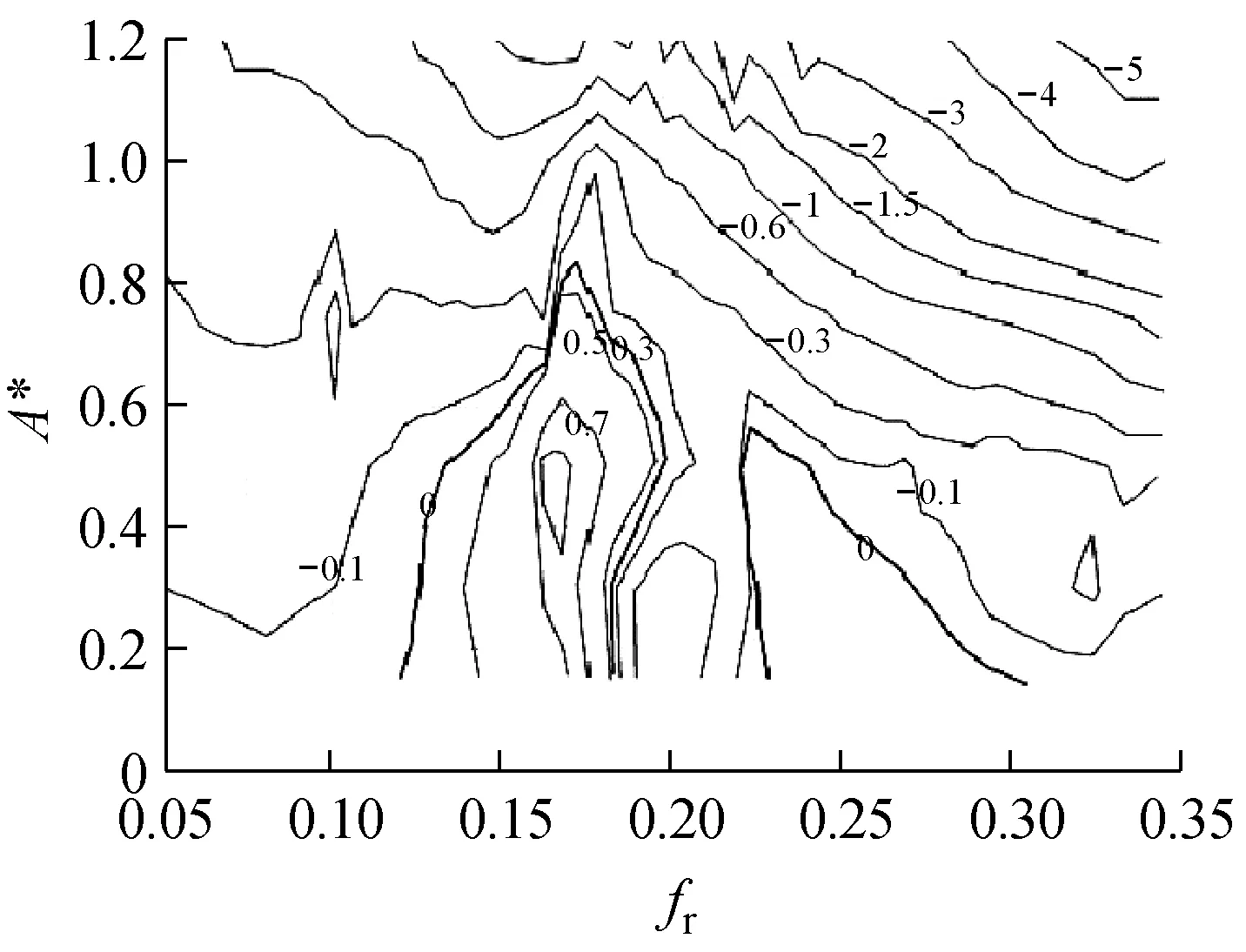
图1 激励力系数云图

1.2 附加质量模型

在2.1节介绍的二维圆柱体受迫振动试验中，Gopalkrishnan还得到了涡激振动下立管附加质量系数云图，如图2所示。与激励力系数类似，附加质量系数也由无因次频率及无因次幅值共同决定。

考虑到由无因次频率变化引起的附加质量系数的偏差远大于无因次幅值改变造成的偏差，本文将上述三维附加质量系数云图简化为仅与无因次频率相关的二维附加质量系数曲线，如图3所示。不难发现，当无因次频率落在[0.15，0.2]区间内时，附加质量系数变化相当剧烈，而这个区间处于涡激振动激发区间内，因此可以认为涡激振动预报时附加质量系数变化效应对预报结果产生一定的影响。

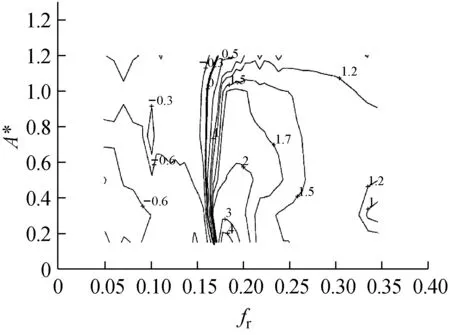
图2 附加质量系数云图

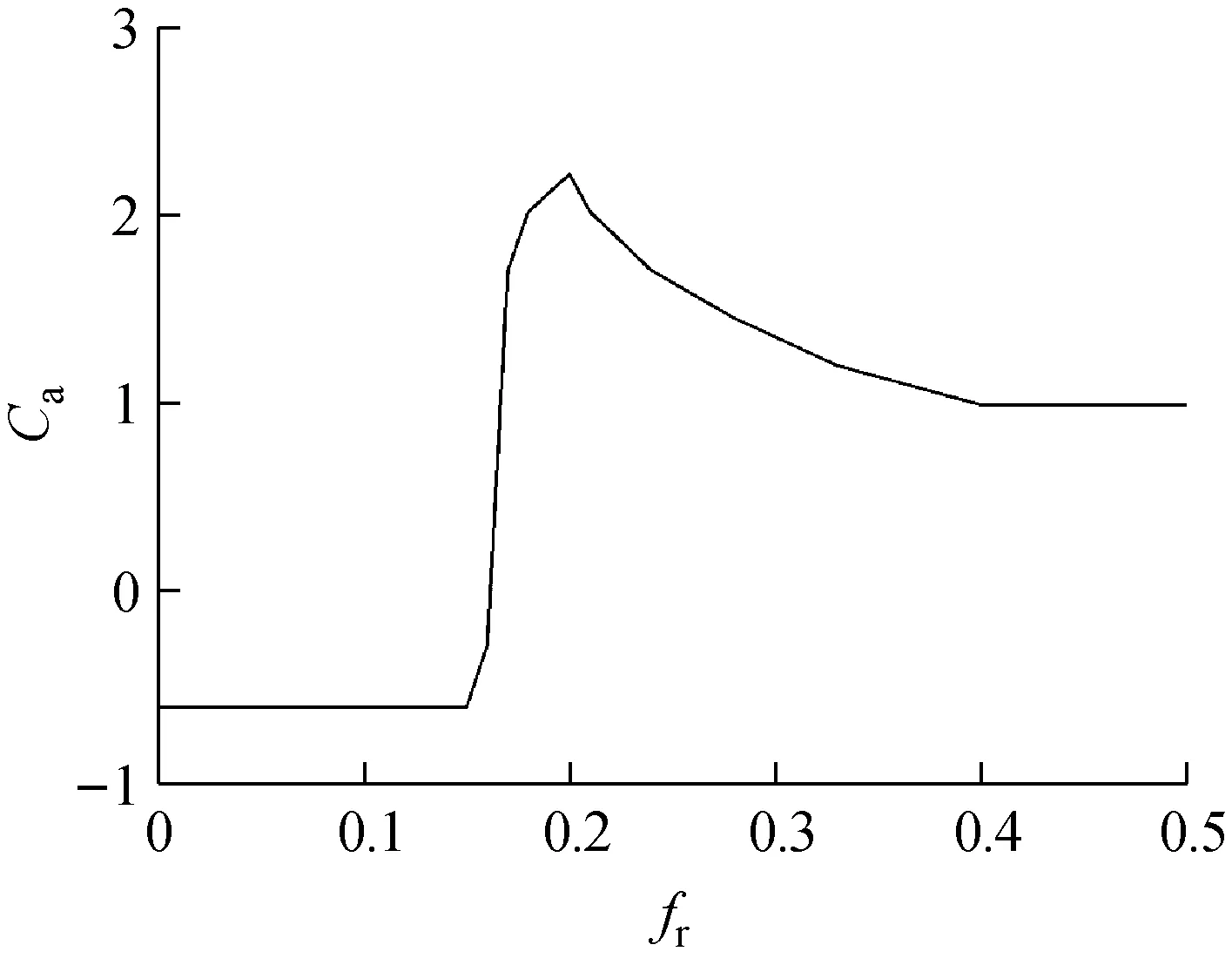
图3 附加质量系数简化曲线

本文认为涡激振动的整个过程中立管各分段的附加质量系数随无因次响应频率的变化而改变。为了更加准确地利用Gopalkrishnan发布的试验数据，无因次频率需要通过式(4)进行修正，以消除由于真实环境及试验条件下Strouhal数不同而产生的误差。除此之外，对于非均匀流工况，由于各水深条件下流速不同的特点，同一根立管不同位置的无因次频率并不相等，不同立管分段对应的附加质量系数也不尽相同，而立管的固有频率由立管自身质量与沿管长方向积分所得总体附加质量决定，因此每个分析步内由无因次频率得到各个立管分段附加质量系数后需要沿管长方向求取平均值，以代入下一分析步进行模态分析，在每一个分析步内，计算附加质量力、确定涡激振动主导频率以及锁定判定均依托于实时附加质量系数

(4)

1.3 锁定判定准则

立管涡激振动的响应幅值和频率是计算水动力载荷最为关键的输入参数，因此在每一个分析步内，需要提取节点位移(u)、节点速度(v)以及当前时刻(t)以确定立管每一个单元的实时响应幅值及频率。立管振动幅值Aosc和频率fosc可通过式(5)得到

Aosc=|ub-ua|/2

fosc=1/[2×(tb-ta)]

(5)

式中:ua,ub,ta,tb为相邻两个v= 0 的时刻点a和b对应的位移和时刻。

本文选取无因次频率锁定区间为[0.125,0.2]，该锁定区间需要根据真实环境采用式(4)进行Strouhal数修正。根据激励力系数云图，无因次频率为0.17对应最大的激励力系数。若无因次振动频率落在锁定区间内，锁定发生，立管单元将锁定到距离锁定中心无因次频率0.17最近的立管自身固有频率上，上述锁定的固有频率则认为是涡激振动主导频率，用于计算激励力。需要指出的是，每一分析步内的立管固有频率均为可变量，需要在当前附加质量系数下进行更新。若无因次振动频率在锁定区间外，认为主导频率等于Strouhal频率，且振动频率用于计算水动力阻尼。本文建立的涡激振动数值分析流程,如图4所示。

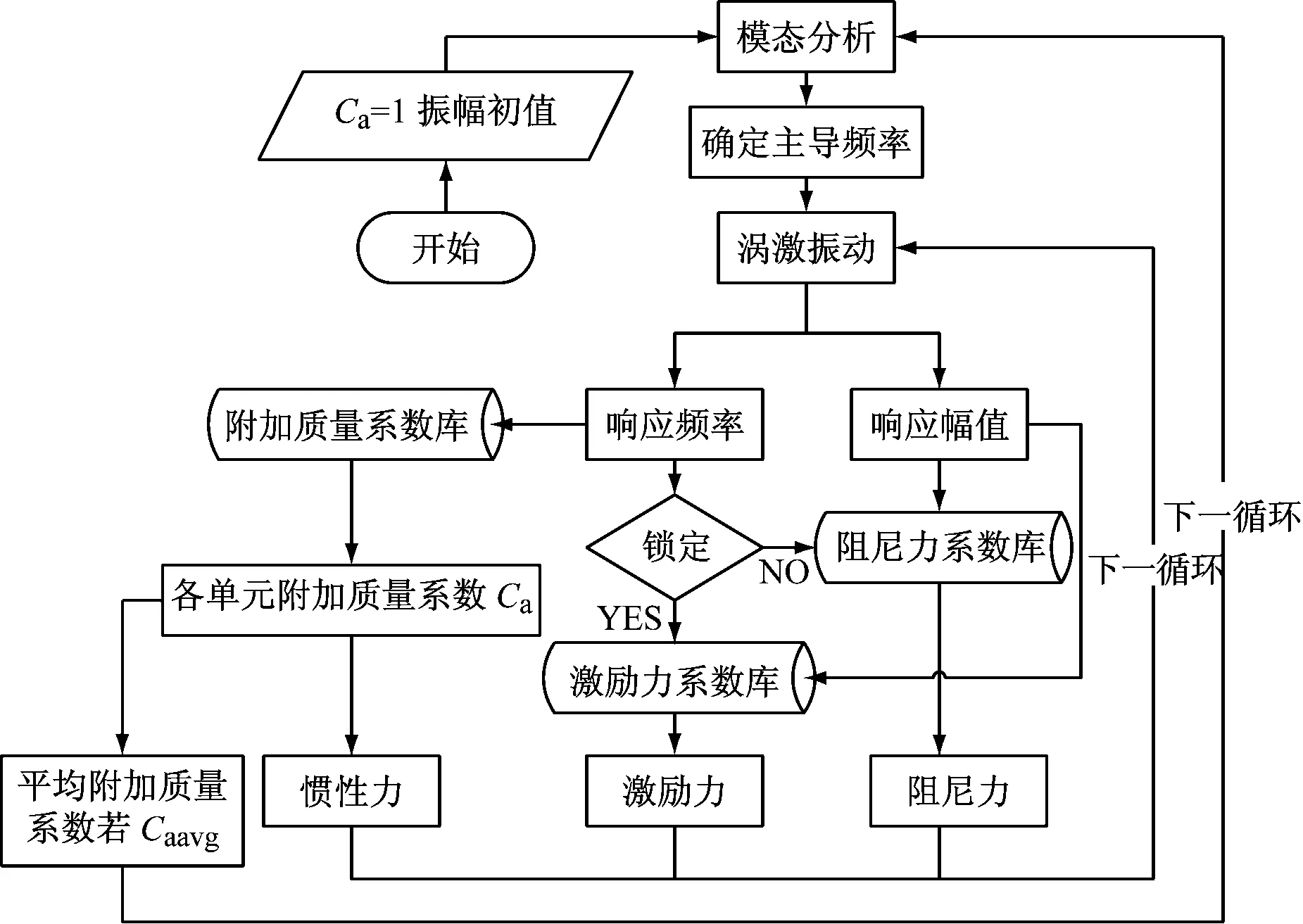
图4 涡激振动时域分析流程图

2 均匀流工况模型试验验证

本章基于提出的涡激振动时域预报方法，以文献[10]中7.9 m小尺度立管模型为研究对象，对目标立管在均匀流条件下涡激振动响应进行数值模拟。均匀流试验装置布置形式如图5所示，当顶部拖车以恒定速度运动时，立管相对于流体处于等效均匀流下，流速从立管底部到顶端均为拖车运行速度U，立管端部侧向拉压装置提供恒定的张紧力。

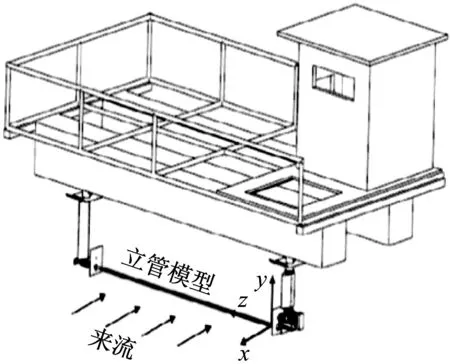
图5 均匀流试验装置示意图

立管模型参数见表1，试验工况对应的雷诺数位于亚临界区域，Strouhal数取0.2。本文选取流速U为2.8 m/s的工况进行预报，为方便更好地对比分析，同时给出附加质量系数恒为1.0情况下的预报结果。

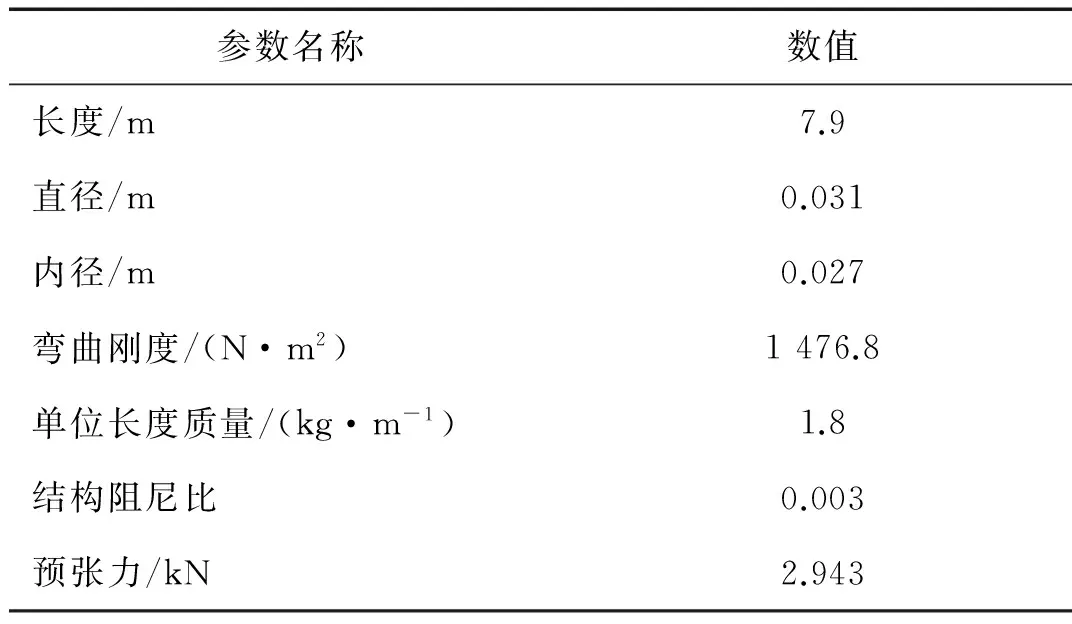
表1 均匀流立管模型参数

2.1 均方根位移对比

计及附加质量系数变化效应与附加质量系数恒为1.0两种不同条件下立管涡激振动均方根位移沿管长分布的包络线以及相应的试验观测结果，如图6所示。结果表明根据本文数值模型预报所得的均方根位移与试验结果吻合较好，仅在立管端部位置略大于试验值，涡激振动激发的均为第5阶模态。对于附加质量系数恒为1.0的数值模型，虽然预报结果显示同样是第5阶模态被激发，但均方根位移幅值沿管长方向均小于试验值，且尤其在立管中部偏差较为明显，可以认为附加质量系数恒为1.0的数值模型未能准确地预报立管实际的涡激振动位移响应。

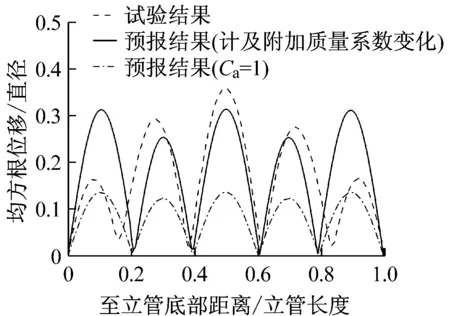
图6 涡激振动均方根位移包络线

2.2 应变响应时历曲线对比

选取立管中点位置(z=3.95 m)处为例，提取应变响应时历曲线并与相应试验结果进行对比。

图7给出两种数值模型预报所得立管中点涡激振动应变响应时历曲线，可以发现计及附加质量系数变化效应的数值模型预报所得应变响应范围与试验值较为接近，均近似在-7.5×10-4～7.5×10-4之间，且时间历程相似，呈现出明显的正弦变化规律。而对于附加质量系数恒为1.0的数值模型，同样呈现出规律的正弦振型，但应变响应范围预报结果远小于试验值，约为-3.0×10-4～3×10-4之间。

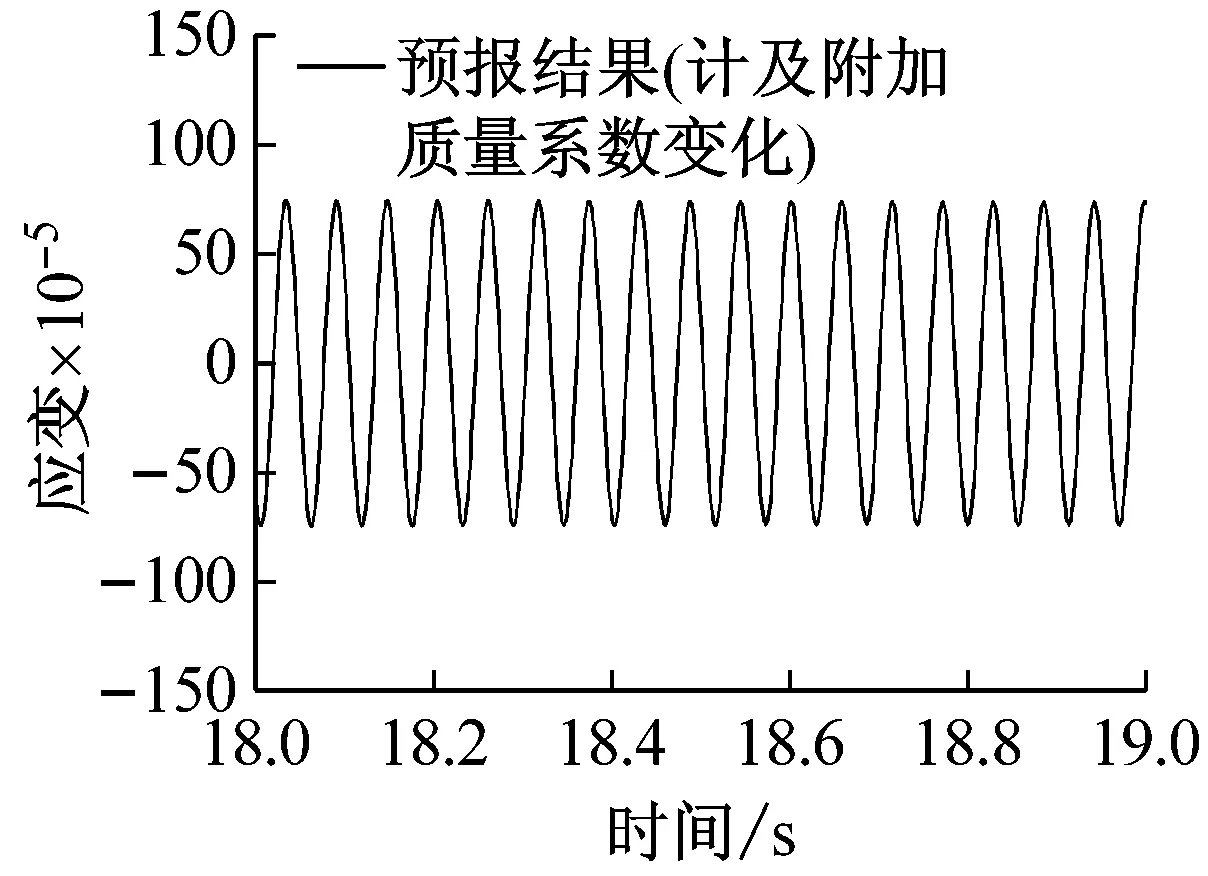
(a)

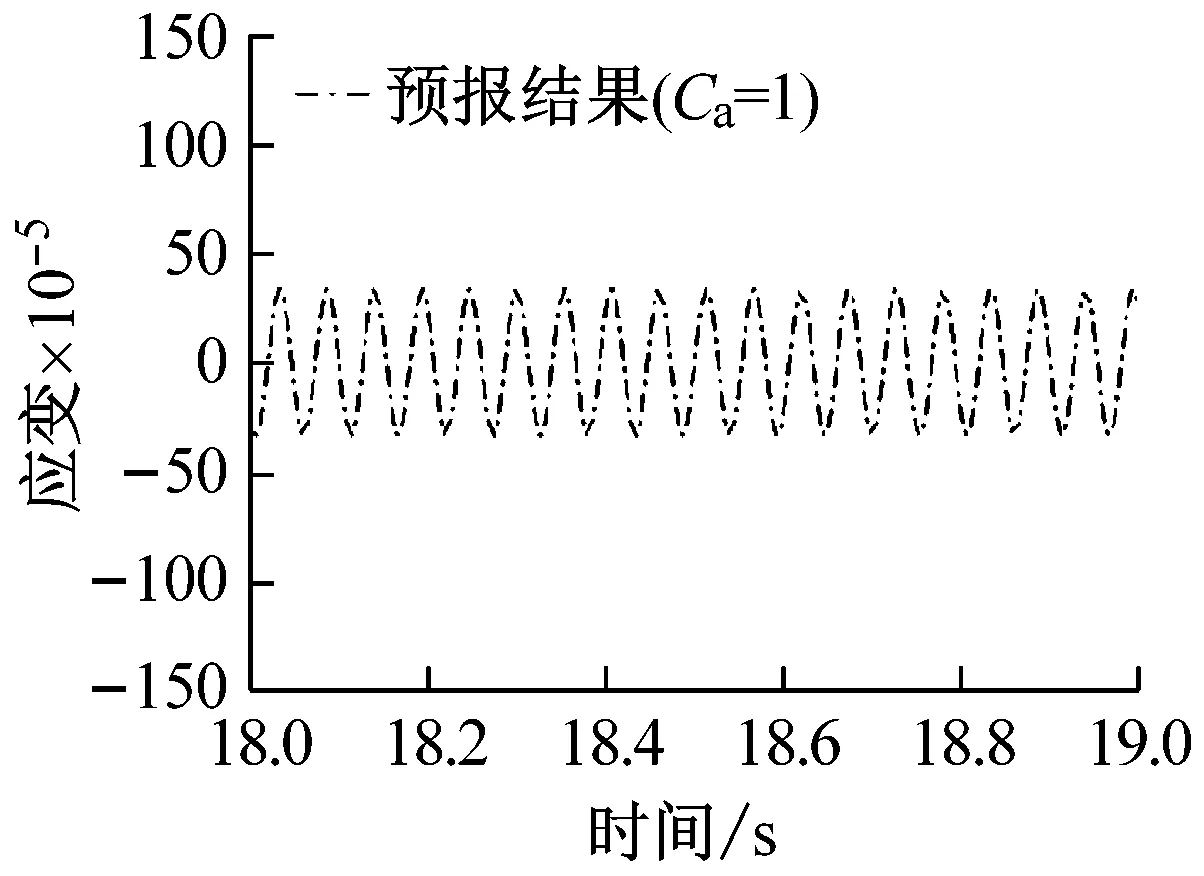
(b)

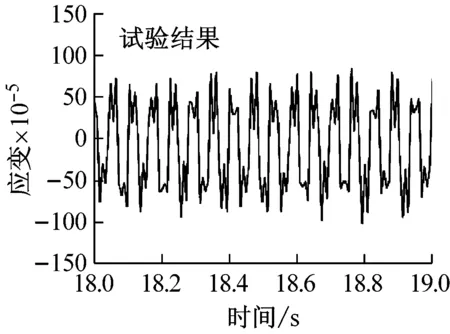
(c)

2.3 应变响应频率对比

对图7中各涡激振动应变响应时历曲线进行傅里叶变换即可得到立管中点应变响应幅值谱，如图8所示。均匀流条件下，预报所得立管横向涡激振动应变响应幅值谱呈现出明显的单一频率主导，计及附加质量系数变化效应的数值模型预报所得主导频率为17.60 Hz，附加质量系数恒为1.0的数值模型预报值为18.71 Hz，相较试验值16.78 Hz，显然计及附加质量系数变化效应的数值模型更为接近，而附加质量系数恒为1.0的传统数值模型预报所得与实际测量值相差2 Hz之多。

由图8可知，试验中观测到对应于50.41 Hz(约为主导频率的三倍)的高频成分同时被激发的现象。由于目前基于受迫振动试验结果建立的流体力数据库针对三倍于主导频率的高频区间的流体力信息尚不完善，本文主要关注单一主导频率下的涡激振动响应，暂未考虑上述高频响应成分。

2.4 附加质量系数对比

由于均匀流场的流速特点，沿管长方向流速恒定，同一时刻立管各处无因次频率相等，根据简化附加质量系数变化曲线所得附加质量系数相等，因此涡激振动进入稳态后附加质量系数平均值也将趋近于某一常数。图9给出本文推荐的数值模型预报所得附加质量系数以及相应的试验实测结果，数据点为沿管长分布各点附加质量系数，虚线为由试验离散结果所得的平均值，实线为本文模型预报值。结果表明，涡激振动过程中附加质量系数的确普遍不等于1.0，本文预报值为1.423，相较通常假定的常数1.0更为接近试验实测结果的平均值。因此，计及附加质量系数变化效应的数值模型更能反映涡激振动响应的真实情况。

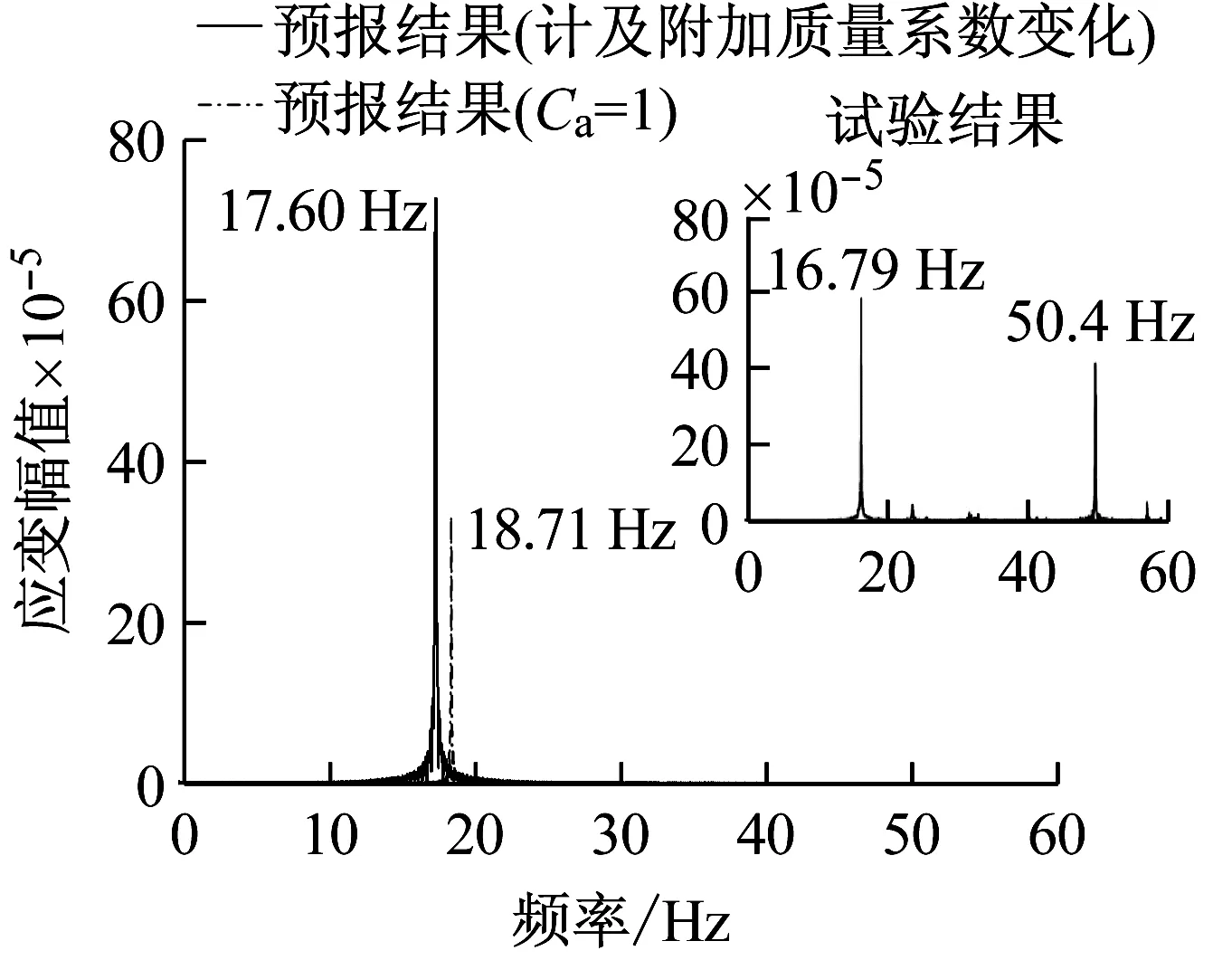
图8 立管中点涡激振动应变响应幅值谱

图9 涡激振动附加质量系数沿管长分布

3 剪切流工况模型试验验证

本章以文献[11-12]中90 m大尺度立管模型为研究对象，对其在线性剪切流条件下涡激振动响应进行数值模拟。剪切流试验装置布置形式如图10所示，当顶部拖车以不同速度运动时，立管便等效于处于不同剪切流下，流速从立管底部的0 m/s到顶端的最大流速Umax成线性分布，与立管底部连接的浮力筒用来提供恒定的张紧力。表2为立管模型参数，St数为0.17。本文选取顶端最大流速Umax为0.54 m/s的工况进行预报，同样给出附加质量系数恒为1.0情况下的预报结果。

3.1 均方根位移及均方根曲率对比

图11和图12分别给出了计及附加质量系数变化效应与附加质量系数恒为1.0两种不同条件下立管涡激振动均方根位移和均方根曲率沿管长的分布以及相应的试验观测结果。图11表明根据本文推荐的数值模型预报所得的均方根位移与试验结果吻合较好，仅在立管顶部略高于试验值，涡激振动激发的均为第11阶模态。对于附加质量系数恒为1.0的数值模型，虽然同样可以预报得到相同阶的模态振型，但在立管顶部及中部与试验结果的吻合度明显不如计及附加质量系数变化效应的数值模型，尤其在立管0.4 L～0.7 L段预报结果明显大于试验值，整体趋势也存在较大偏差。由图12可知，本文的数值模型预报所得均方根曲率同样与试验结果给出的散点数据贴合较好，即使在立管顶部也基本一致，激发模态与均方根位移呈现的振型相对应，仍为第11阶。然而由附加质量系数恒为1.0的数值模型预报得到的均方根曲率表现出主导模态为12阶的现象，且同样在立管0.4 L～0.7 L段与试验结果存在较为清楚的差别，较试验值偏小，这也在一定程度上解释了为何均方根位移在立管中部与试验结果出现偏差。

图10 剪切流试验装置示意图

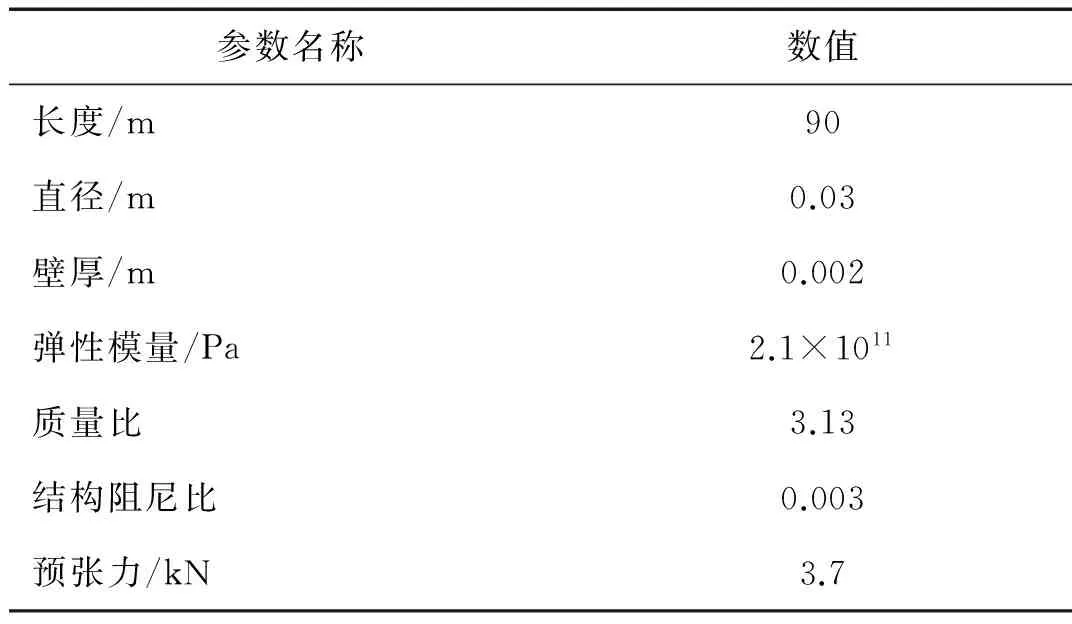
参数名称数值长度/m90直径/m0.03壁厚/m0.002弹性模量/Pa2.1×1011质量比3.13结构阻尼比0.003预张力/kN3.7

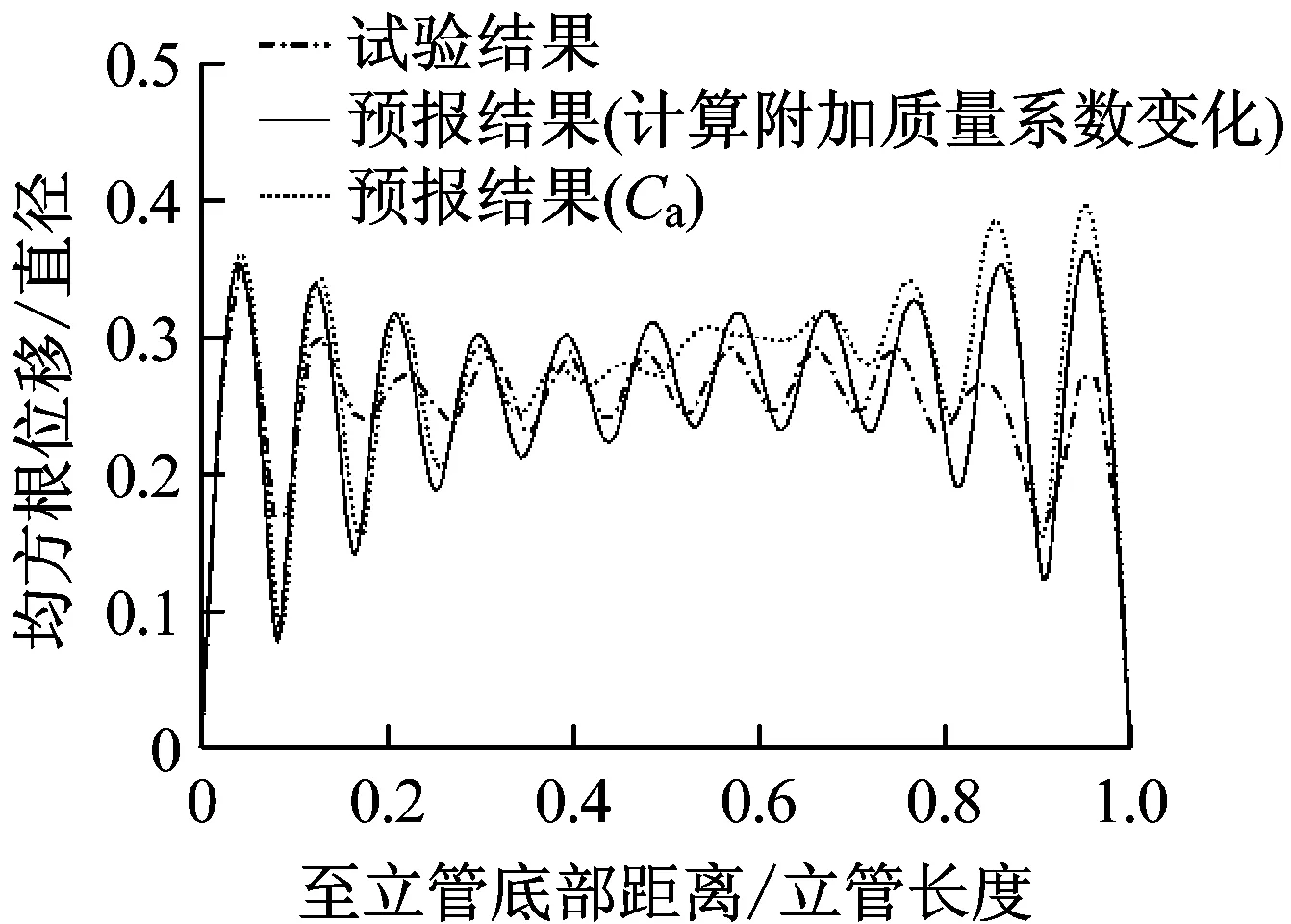
图11 涡激振动均方根位移包络线

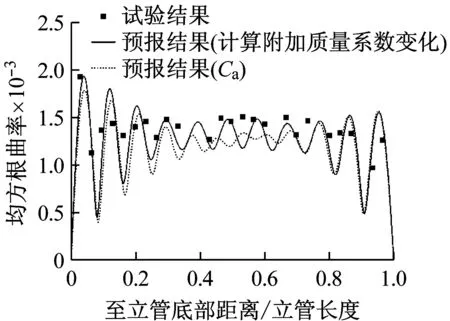
图12 涡激振动均方根曲率包络线

3.2 位移响应时历曲线对比

选取立管中点位置(z=45 m)处为例，提取位移响应时历曲线并与相应试验结果进行对比。两种数值模型预报所得立管中点涡激振动位移响应时历曲线如图13所示，可以发现计及附加质量系数变化效应的数值模型预报所得位移响应范围与试验结果非常接近，近似位于-0.02 m～0.02 m，且最小均振幅小于0.05 m，振幅变化规律也较为相似。而对于附加质量系数恒为1.0的预报结果，位移响应最大振幅约为0.16 m，略小于试验值，且最小振动幅值达到了0.06 m，较试验值偏大。

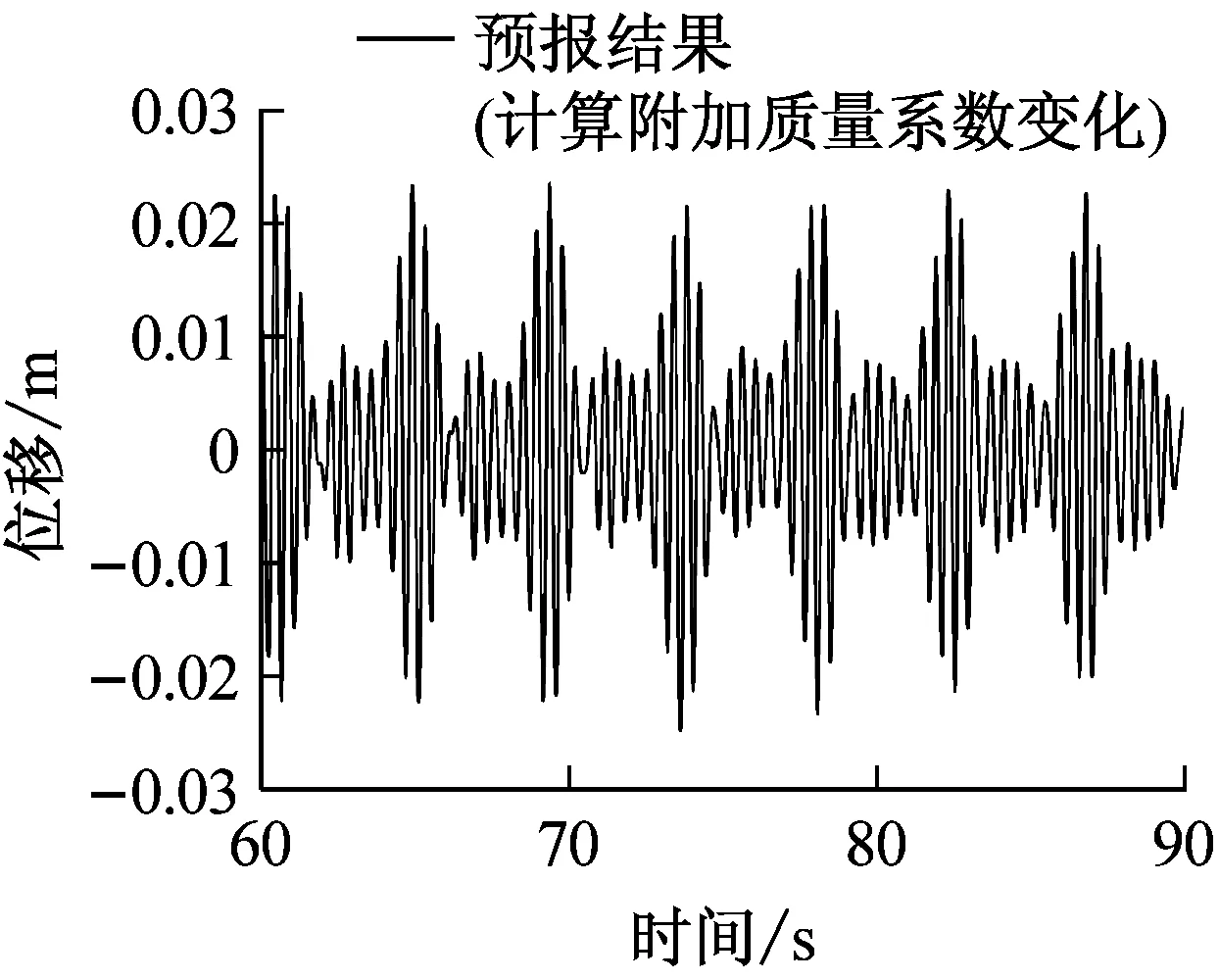
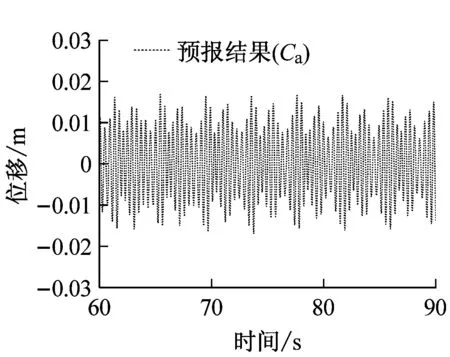
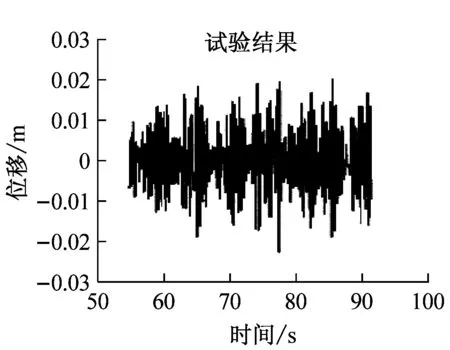
图13 立管中点位置涡激振动位移响应时历曲线

3.3 位移响应频率对比

对图14中各涡激振动位移响应时历曲线进行傅里叶变换即可得到立管中点位移响应幅值谱，如图14所示。由于背景来流为剪切流，有别于均匀流条件，立管横向涡激振动位移响应幅值谱呈现出明显的多频率叠加现象。试验观测结果表明主导频率为2.13 Hz，主要有3阶频率参与振动。计及附加质量系数变化效应的数值模型预报的主导频率为2.23 Hz，同样主要有3阶频率被激发，且位移响应幅值谱整体形状与试验结果非常接近。对于附加质量系数恒为1.0的数值模型，虽然预报的参与涡激振动的频率数与幅值谱的形状和真实值相似，但主导模态显示为2.44 Hz，相较计及附加质量系数变化效应的数值模型，与试验值偏差明显。两套预报结果与试验数据均表明，被激发频率范围大致为2～3 Hz。

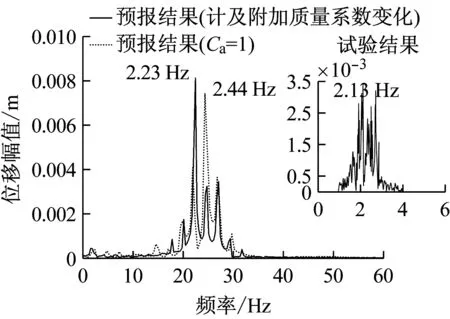
图14 立管中点涡激振动位移响应幅值谱

剪切流条件下立管各处遭遇流速各不相同，同一时刻立管不同位置处对应的无因次频率也不尽相等，且由于涡激振动呈现出明显的多阶模态叠加现象，即使振动进入稳态，不同时刻立管的响应频率也不尽相等，平均附加质量系数呈现时变规律。以参与振动的主导频率第11阶固有频率2.13 Hz为例，该阶模态主导振动时由简化附加质量系数变化曲线得到的平均附加质量系数为1.847，与通常假定的1.0存在较明显的差距。

4 结 论

本文针对海洋立管涡激振动问题提出了一套计及附加质量系数变化效应的时域预报方法。立管所受水动力载荷与振动幅值及响应频率耦合关联，在时域内迭代求解，同时考虑了附加质量系数随响应频率改变的变化效应。涡激振动主导频率由实时附加质量系数下立管固有频率、Strouhal频率以及响应频率共同决定。

通过模拟某7.9 m小尺度试验立管在均匀流下以及某90 m大尺度试验立管在线性剪切流下的涡激振动响应并将预报结果与试验结果进行对比，本文计及附加质量系数变化效应涡激振动时域预报模型的可行性及准确性得到了证实，并在此基础上得到了以下结论：

(1) 本文时域预报模型得到的均方根位移及曲率、应变及位移响应时历、响应幅值谱以及附加质量系数均与试验结果吻合，预报所得涡激振动主导模态及振型也与试验观测结果符合性较好。本文数值模型对于非均匀流条件下深海立管涡激振动响应预报同样适用。

(2) 对比计及附加质量系数变化效应与附加质量系数恒为1.0的数值模型，前者预报准确度更优，附加质量系数变化效应对预报结果的影响不宜忽略。尤其是在均匀流工况下对于振动位移和应变幅值以及剪切流工况下对于均方根曲率的预报时，附加质量系数变化效应的影响更为显著，本文推荐的数值模型在一定程度上可以较为有效地避免上述问题的出现。

(3) 对比7.9 m和90 m两根试验立管的预报结果，可以发现，附加质量系数变化效应对于小尺度立管模型的影响相比大尺度立管模型更为显著。这是因为，在相同条件下，立管尺度越小，刚度和固有频率越大，附加质量系数的变化对于固有频率的影响也更为明显，且这种影响会随着激发模态阶数的增大而进一步放大。由此推断，对于立管刚度较大，被激发模态阶数较高的工况下涡激振动的预报模型，更应该计及附加质量系数变化效应。

综上，本文提出的涡激振动时域预报程序对现有时域预报程序进行了优化，弥补了未计及附加质量系数变化效应的不足，为更为准确地预报深海立管涡激振动提供一定的参考。本文采用的流体力模型源自亚临界流动区域内受迫振荡试验，对于超出这一流动区域雷诺数范围的涡激振动问题有待今后进一步开展更为深入的试验和理论研究。

[1] VANDIVER J K, LI L. SHEAR7 V4.4 program theoretical manual[M]. Cambridge, MA: Massachusetts Institute of Technology, 2005.

[2] LARSEN C M, LIE H, PASSANO E, et al. VIVANA theory manual (Version3.7)[M]. Trondheim, Norway: Norwegian Marine Technology Research Institute, 2009.

[3] GRANT R, LITTON R, FINN L. Highly compliant rigid risers: Filed test benchmarking a time domain VIV algorithm [C]∥Proceedings of the Offshore Technology Conference. Houston, TX, 2000.

[4] SIDARTA D E, FINN L D, MAHER J. Time domain FEA for riser VIV analysis[C]∥Proceedings of the ASME 2010 29th International Conference on Ocean, Offshore and Arctic Engineering. Shanghai, China: OMAE2010-20688, 2010.

[5] WANG K P, XUE H X, TANG W Y. Time domain analysis approach for riser vortex-induced vibration based on forced vibration test data [C]∥Proceedings of the ASME 2013 32nd International Conference on Ocean, Offshore and Arctic Engineering. Nantes, France: OMAE2013-10285, 2013.

[6] CHEN W M, LI M, GUO S X, et al. Dynamic analysis of coupling between floating top-end heave and riser’s vortex-induced vibration by using finite element simulations [J]. Applied Ocean Research, 2014, 48:1-9.

[7] THORSEN M J, SEVIK S, LARSEN C M. Time domain simulation of vortex-induced vibrations in stationary and oscillating flows [J]. Journal of Fluids and Structures, 2016, 61:1-19.

[8] GOPALKRISHNAN R. Vortex induced forces on oscillating bluff cylinders [D]. Cambridge, MA: Massachusetts Institute of Technology, 1993.

[9] VENUGOPAL M. Damping and response of a flexible cylinder in a current [D]. Cambridge, MA: Massachusetts Institute of Technology, 1996.

[10] SONG L J, FU S X, CAO J, et al. An investigation into the hydrodynamics of a flexible riser undergoing Vortex-Induced Vibration [J]. Journal of Fluids and Structures, 2016, 63: 325-350.

[11] HUSE E, KLEIVEN G, NIELSEN F G. Large scale model testing of deep sea risers [C]∥Proceedings of the Offshore Technology Conference. Houston, TX, 1998.

[12] LIE H, KAASEN K E. Modal analysis of measurements from a large-scale VIV model test of a riser in linearly sheared flow [J]. Journal of Fluids and Structures, 2006, 22(4):557-575.