基于冲击响应谱的导弹冲击试验条件制定与优化方法研究

方诗麟, 卢 梅, 李 铁

(上海机电工程研究所，上海 201109)

导弹在运输、发射和飞行过程中会经历冲击激励，引起导弹的冲击响应，为了确保导弹能够在实际环境中完成任务，导弹需要在设计阶段进行冲击试验验证[1]。

在实际设计阶段尤其是方案阶段，导弹在全寿命周期中的实际冲击响应数据往往不足[2]，导致实验室无法确定试验条件。但理论冲击激励(质心过载)曲线可以通过理论计算在方案阶段得出。因此本文应用冲击响应谱模型进行理论计算，得出了导弹理论冲击响应谱，在与实际遥测数据进行对比验证证实该模型的可行性后，通过自适应差分进化算法[3]进行优化，将试验冲击响应谱与实际冲击响应谱相匹配，得出最优导弹冲击试验条件，达到确定导弹最优冲击试验条件的目的。

1 冲击响应谱

1.1 基本概念

冲击响应谱的定义[4]：一系列单自由度振动系统，在冲击激励函数作用下，它们的冲击响应最大值与系统固有频率之间的关系，定义为冲击激励函数的冲击响应谱。冲击响应谱分析在结构方面的用途主要用来衡量冲击作用的效果，估计冲击对结构的损伤大小。

冲击响应谱分为三种[5]：最大冲击响应谱、冲击初始谱和冲击剩余谱。冲击初始谱指冲击激励过程中系统响应的最大值；冲击剩余谱指冲击激励结束后系统响应的最大值；最大冲击响应谱是冲击初始谱和冲击剩余谱的组合最大值。在工程上，一般采用最大冲击响应谱。

1.2 基本模型

实际的物理系统可以分解为多个不同单自由度系统[6]，对于每个单自由度系统进行冲击响应分析计算，取系统响应最大值，然后和它的固有频率组成一个数据点，最后将这些点用光滑的曲线连接，即可得整个系统的冲击响应谱(图1)。

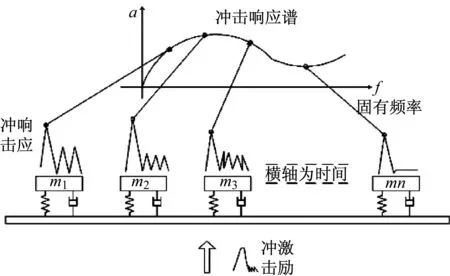
图1 冲击响应谱模型

因此，我们要求得已知冲击激励的冲击响应谱，只要将已知的冲击激励输入、不同固有频率和阻尼比的系统，取其响应的最大值，便可得到冲击激励的冲击响应谱。

针对单个子系统，给出一个典型的基础激励的机械振动冲击系统(图2)，代表一个质量M，弹性系数K，阻尼为C的单自由度系统，输入为基础激励的加速度，输出为质量块的加速度。

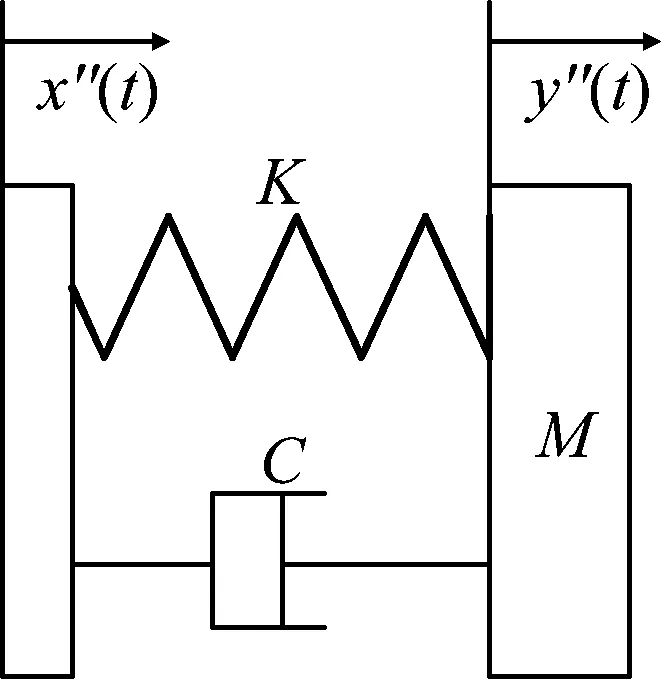
图2 绝对加速度模型

(1)

设

进行拉式变换有：

(ms2+cs+k)Y(s)=(k+cs)X(s)

(2)

则该系统的传递函数是

(3)

1.3 计算仿真

使用MATLAB对实际冲击激励进行计算，可得到实际激励的冲击响应谱；单次冲击响应的仿真(Simulink)如图3所示，每次改变系统的固有频率，循环进行计算即可。

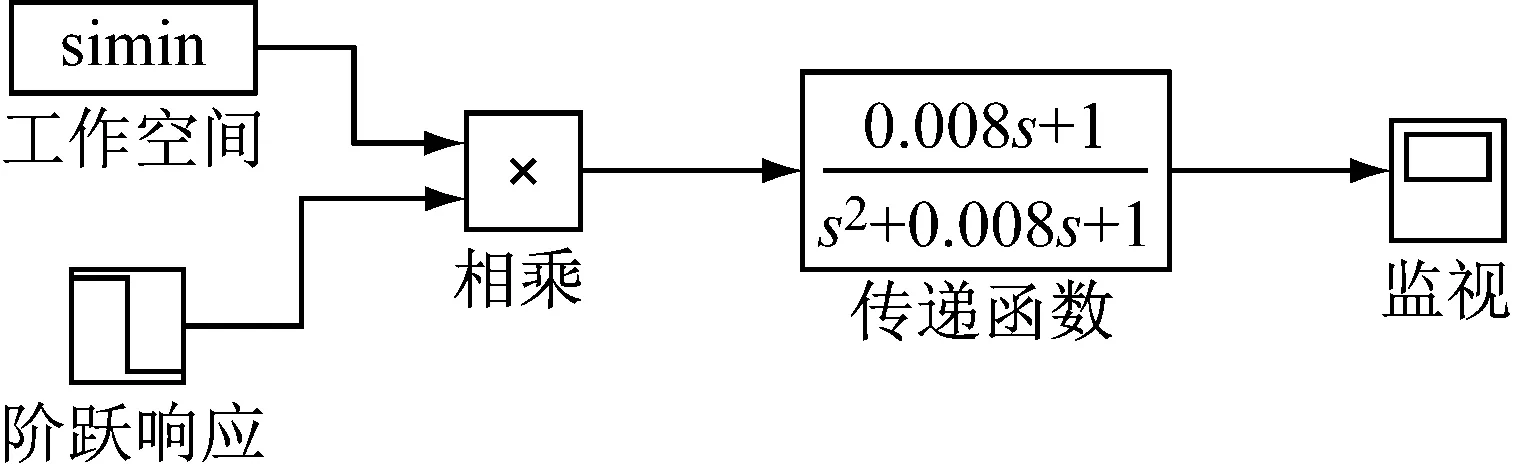
图3 Simulink仿真平台

每次计算后，取固有频率和对应的最大值做为一个数据点，遍历我们关心的固有频率范围，最后就得到冲击激励的冲击响应谱。

2 冲击试验条件制定方法

2.1 前提条件

当满足下列4个条件时，即可应用本套方法：

各控制点的冲击响应曲线未知(无实测数据)；

可以确定系统的输入激励；

通过与试验场所沟通，得知试验设备的标准输入激励波形，持续时间和幅值范围；

通过以往经验或前期计算，得知导弹X，Y和Z向的一阶固有频率范围。

2.2 冲击试验条件制定流程图

冲击试验条件制定流程图，如图4所示。

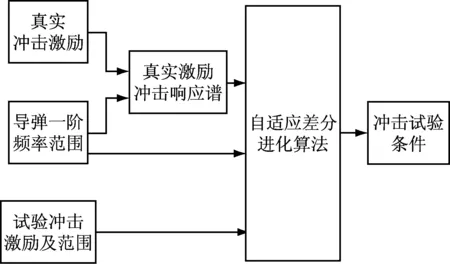
图4 冲击试验条件制定流程图

输入为真实冲击激励、导弹一阶频率范围和试验冲击激励及范围；由真实冲击激励和导弹一阶频率范围可计算得到真实激励下在频率范围内的冲击响应谱；再由真实激励下的冲击响应谱和试验冲击激励及范围作为优化阶段的输入，经过自适应差分进化算法优化，计算得到冲击试验条件。

真实冲击激励：导弹飞行过程中的质心过载、空空导弹挂飞过程中飞机吊挂点的过载等等。

导弹一阶频率范围：导弹x，y和z向的一阶固有频率范围，一般根据以往设计经验可以得到一个范围。

试验冲击激励及范围：试验设备的输出波形、输出幅值范围和脉冲宽度范围。

真实激励冲击响应谱：由真实冲击激励作为输入，得到一阶固有频率范围内的冲击响应谱。

自适应差分进化算法：引入自适应参数IM，改善传统的差分进化算法，前期提高全局搜索能力，后期提高局部搜索能力，具体算法见2.3节。

冲击试验条件：冲击激励波形、输出幅值和脉冲宽度。

2.3 自适应差分进化算法

冲击试验条件优化的数学模型：

min ∑(A(f)-At(f))2

(4)

s.t.Amin≤A≤Amax

Tmin≤T≤Tmax

A(f)≥At(f) for allf

(5)

式中：Amin试验设备输出幅值最小值；Amax试验设备输出幅值最大值；Tmin试验设备输出脉宽最小值；Tmax试验设备输出脉宽最大值；A(f)试验激励的冲击响应谱；At(f)真实激励的冲击响应谱。

针对冲击试验条件的优化选择，自适应差分进化算法按如下方式实现：

A初始化种群

随机产生n组向量(个体)的种群，每组向量由两位构成[A,T]，A为试验输出波形幅值，T为试验输出波形脉宽(A和T的范围见2.2节)。

(6)

(7)

B变异操作

在当代种群中随机选出三组个体，生成变异染色体：

(8)

其中：F为变异系数，直接反应变异个体与当代种群的差异性。

C交叉操作

(9)

D选择操作

约束范围内

(10)

不在约束范围内

Ffitness(x)=-2

(11)

本文采用自适应差分进化算法，与传统差分进化的区别在于：其前期全局搜索能力强，容易跳出局部最优解；后期局部搜索能力强，容易收敛。

引入参数IM，表示上一代与当前一代最佳适应度之比。在搜索前期，适应度变化大，IM值小，有利于提高全局搜索能力和多样性；在搜索后期，适应度变化小，IM值大，有利于提高局部搜索能力以及加快收敛能力。

(12)

(13)

式(13)中：F和CR分别是变异系数和交叉系数，反应产生新个体与原个体的差异性和新个体留存下来的概率。F和CR值越大，全局搜索能力越强，容易跳出局部最优解；反之，局部搜索能力提高，收敛性更强。

自适应差分进化算法的核心思想是，将差分进化算法中的各个参数，根据迭代前后两代种群的适应度情况进行自适应调节，大大提高了差分进化算法的鲁棒性和搜索性能。

3 实例应用

首先通过产品质心过载，计算其冲击响应谱，然后与遥测数据对比，验证利用冲击响应谱衡量系统冲击响应的合理性；根据试验激励的曲线、幅值和持续时间范围，利用差分进化算法可得到最优的试验条件。

3.1 理论计算与遥测对比验证

根据导弹质心纵向、俯仰和偏航三个方向的过载，可计算其冲击响应谱；在飞行试验过程中，可以通过遥测得到纵向、俯仰和偏航三个方向响应。对比频率范围内的冲击响应谱值与真实响应值，验证冲击响应谱的准确性。

因此我们截取出过载中突变的过程作为输入激励，将下面三个方向的过载截取出来，如图5。

根据以往资料，我们假设导弹的一阶固有频率在40 Hz和60 Hz之间，阻尼比假设为0.008 0。代入模型计算仿真，分别得到纵向、俯仰和偏航的冲击响应谱(图6)。

根据以往的经验，导弹的x，y和z向的在40 Hz和60 Hz之间。

(a)纵向输入激励

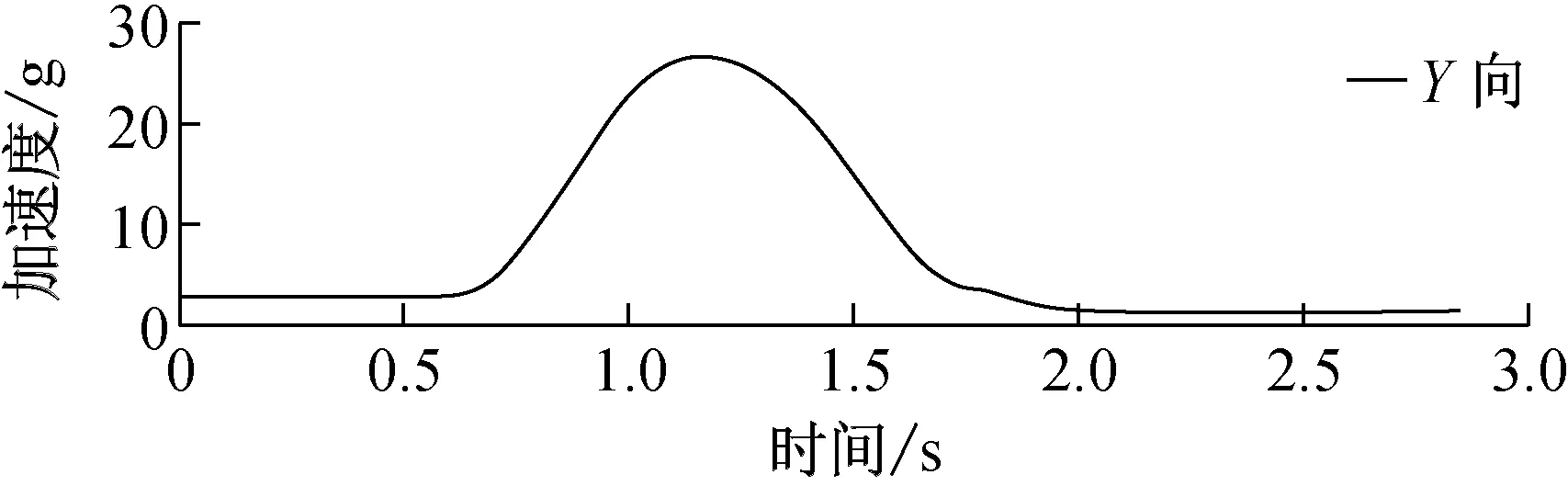
(b)俯仰输入激励

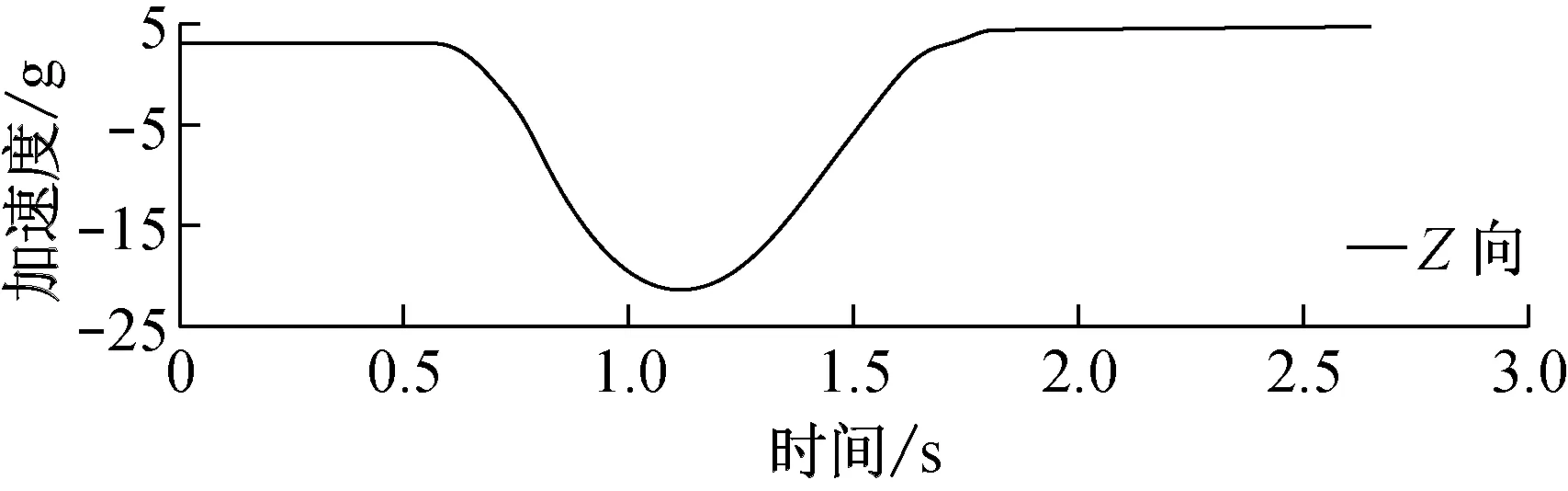
(c)偏航输入激励

(a)纵向输入激励的冲击响应谱

(b)俯仰输入激励的冲击响应谱

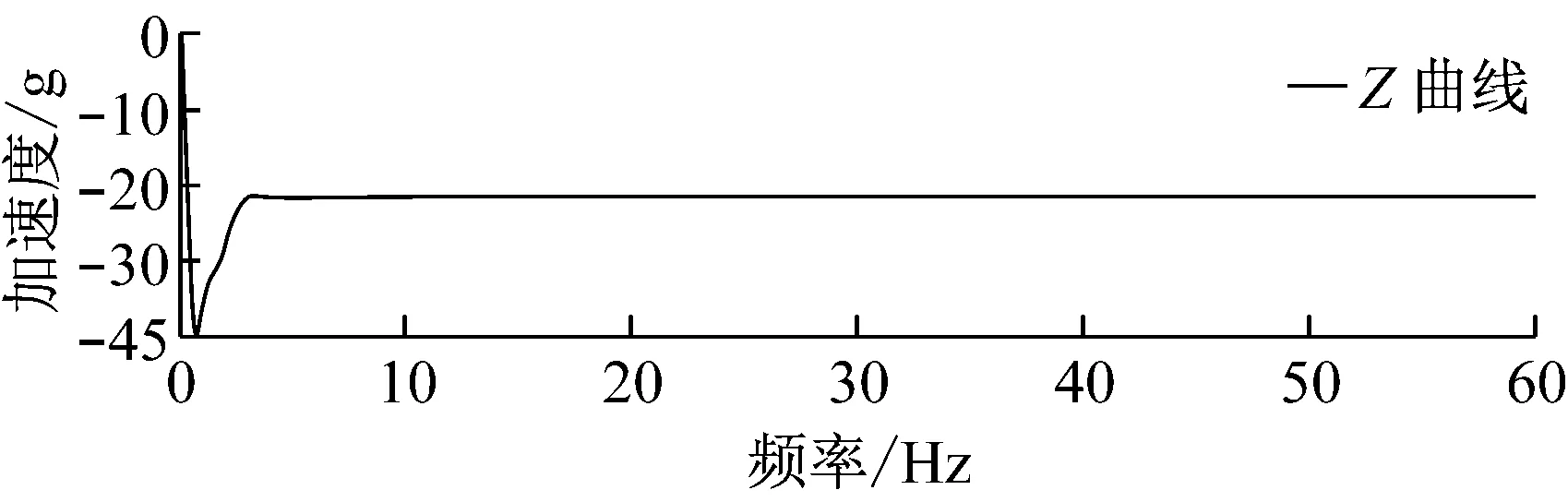
(c)偏航输入激励的冲击响应谱

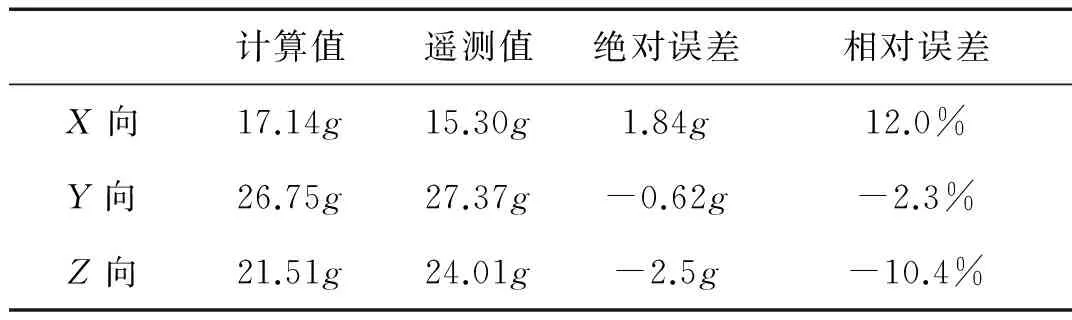
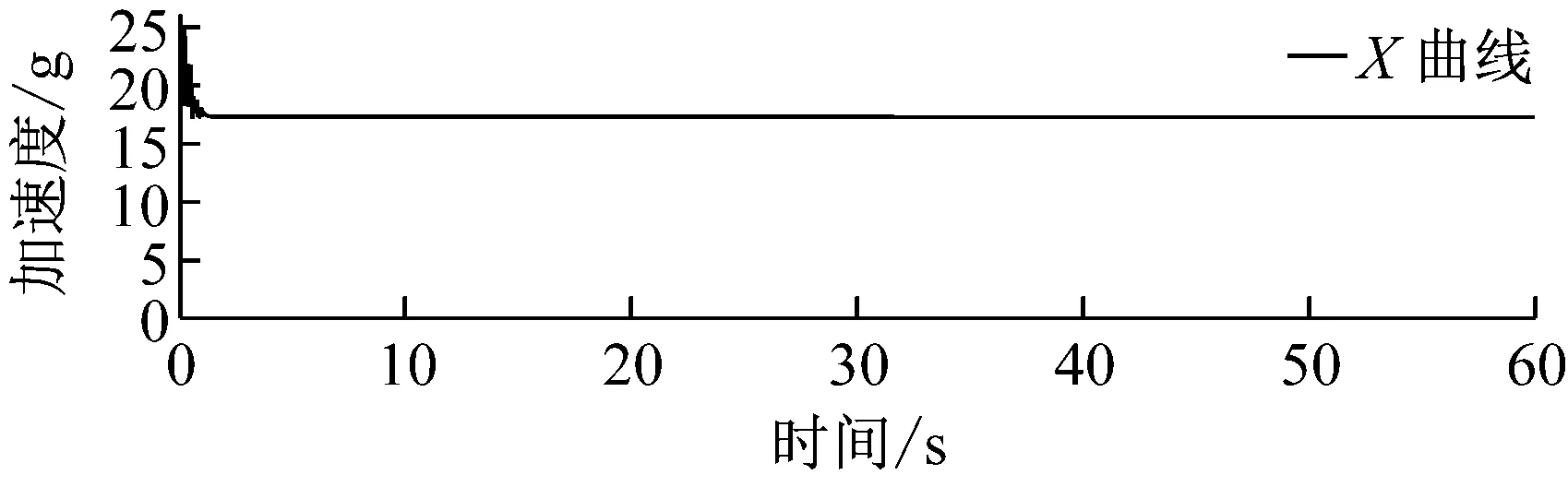
计算值遥测值绝对误差相对误差X向17.14g15.30g1.84g12.0%Y向26.75g27.37g-0.62g-2.3%Z向21.51g24.01g-2.5g-10.4%

对比上表中数据，计算值和遥测值的相对误差在12.0%之内，而且可以看出是随机误差，不是系统误差，是由于对于系统的阻尼比估算不准，遥测误差等误差造成的。

根据验证与对比，可以认为根据冲击激励估算系统响应的方法基本符合现有的要求，也为下一步制定冲击试验条件提供了理论依据。

3.2 冲击试验条件的优化计算

一般试验设备都能输出半正弦波，因此在接下来确定冲击试验的过程中，只要确定试验冲击的幅值A和持续时间T，该实例中试验冲击的冲击响应在40 Hz和60 Hz之间包络对应的理论冲击响应谱。

在实际试验制定过程中，一般留有50%的余量，即提高50%的裕度之后对应纵向、俯仰和偏航的响应值(At)分别为：25.71g、40.13g和32.27g。

接下来使用自适应差分进化算法来找到最优的试验冲击曲线(确定幅值A和持续时间T的半正弦波)。

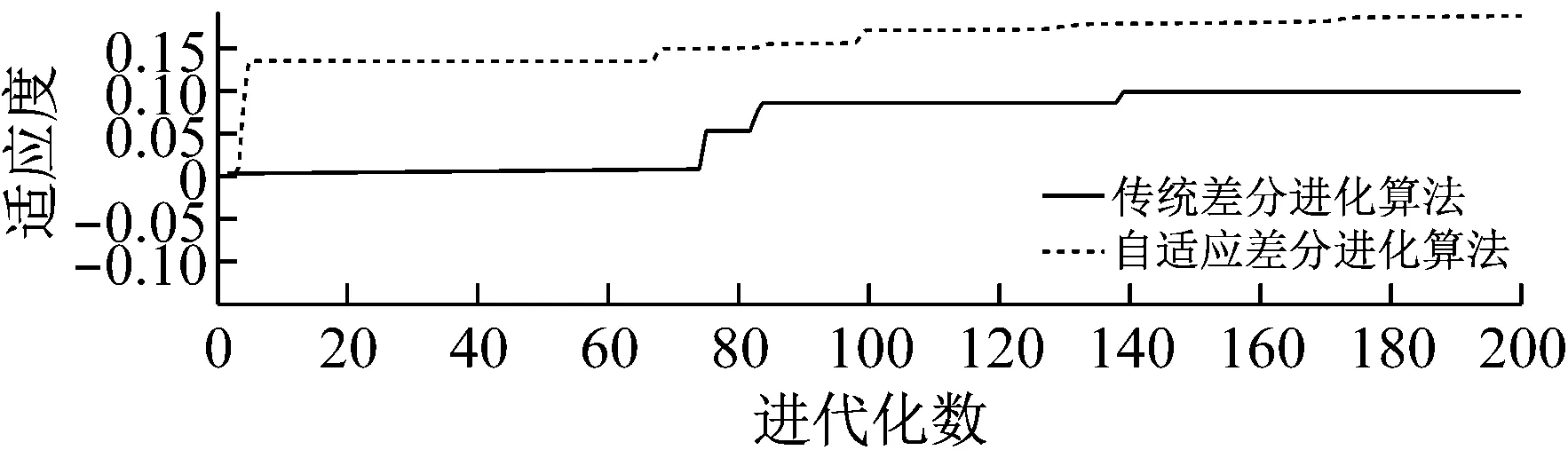
自适应差分进化算法和传统差分进化算法的适应度曲线对比如图7。

(a)x向适应度曲线

(b)y向适应度曲线

(c)z向适应度曲线

从图7中可以发现，自适应差分进化算法的适应度曲线在200代时，达到的适应度比传统差分进化算法高，也就说明由自适应差分进化算法得到的试验冲击曲线更优。

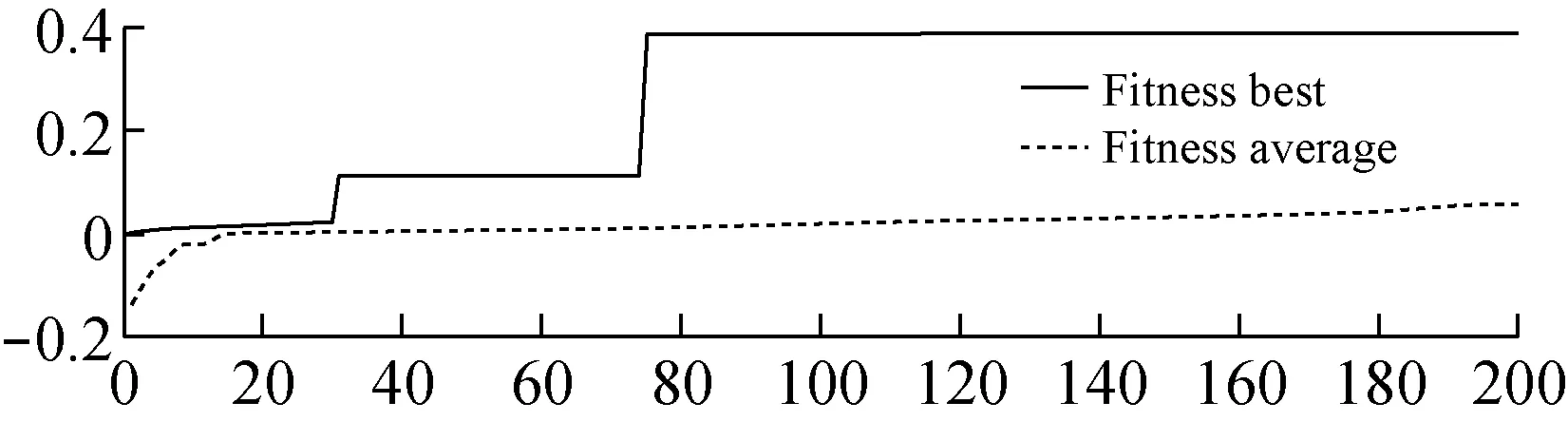
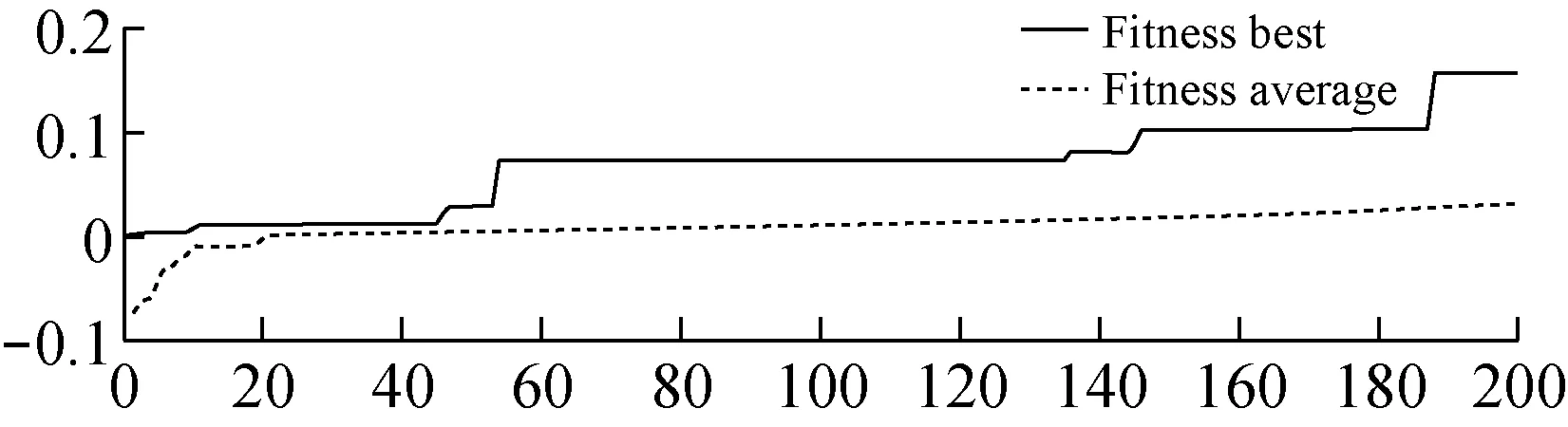
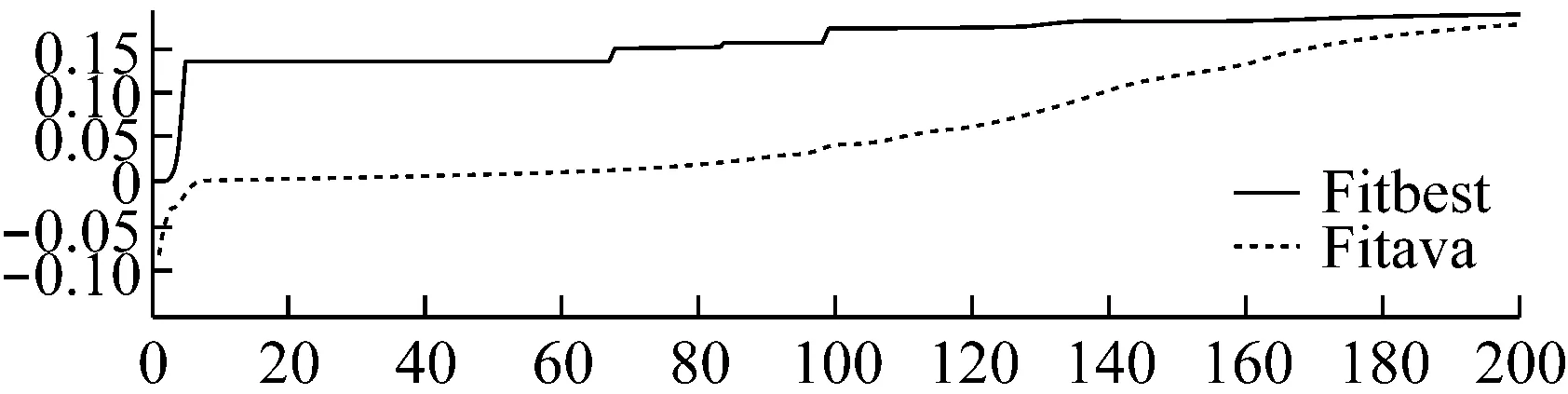
用传统差分进化算法优化时，由于变异因子F与交叉因子CR是常数，因此收敛速度很慢，如图8所示200代时还未收敛。

自适应差分进化算法中，引入参数IM,进而引入了自适应的变异因子F和交叉因子CR，使得收敛速度变快，如图9所示200代就已经收敛。

经过自适应差分进化算法优化计算后，最后得到对应的试验条件(表2)。

(a)x向适应度曲线

(b)y向适应度曲线

(c)z向适应度曲线

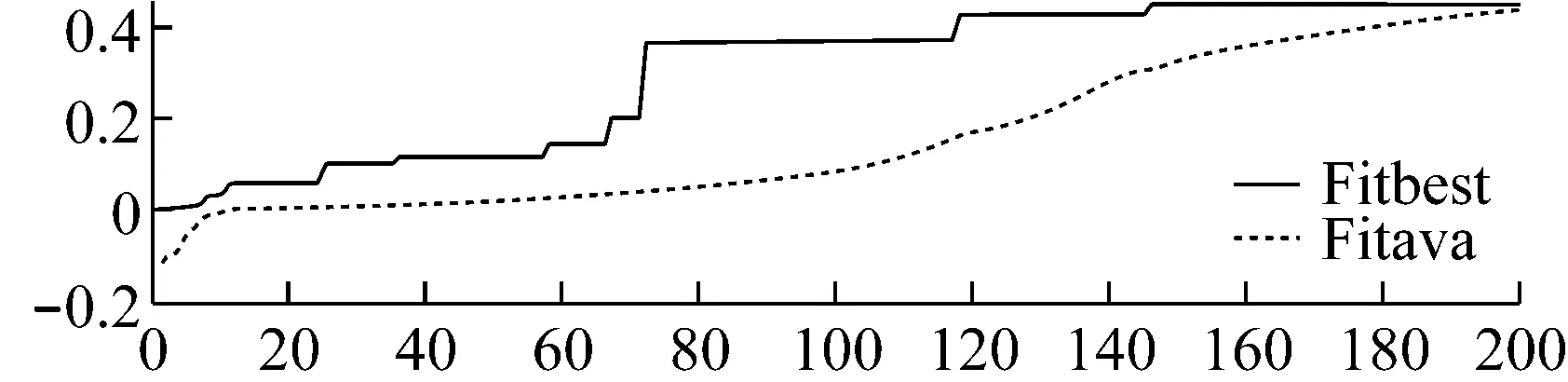
(a)x向适应度曲线

(b)y向适应度曲线

(c)z向适应度曲线

幅值Ain/g持续时间T/sX向(纵向)15.060.0166Y向(俯仰)23.510.0166Z向(偏航)18.910.0166

使用表2的试验条件，通过计算得到试验的冲击响应谱，与实际冲击响应谱对比，如图10所示。

4 结 论

针对导弹在研制阶段初期实测数据不足，导致无法科学确定导弹冲击试验条件这一问题，本文根据质心理论过载曲线，应用冲击响应谱模型进行理论计算，得出了导弹理论冲击响应谱，并与实际遥测数据进行对比验证，证实该模型的可行性。然后，通过自适应差分进化算法进行优化，将试验冲击响应谱与实际冲击响应谱相匹配，得出最优导弹冲击试验条件，为导弹在研制阶段确实冲击试验条件提供理论依据。

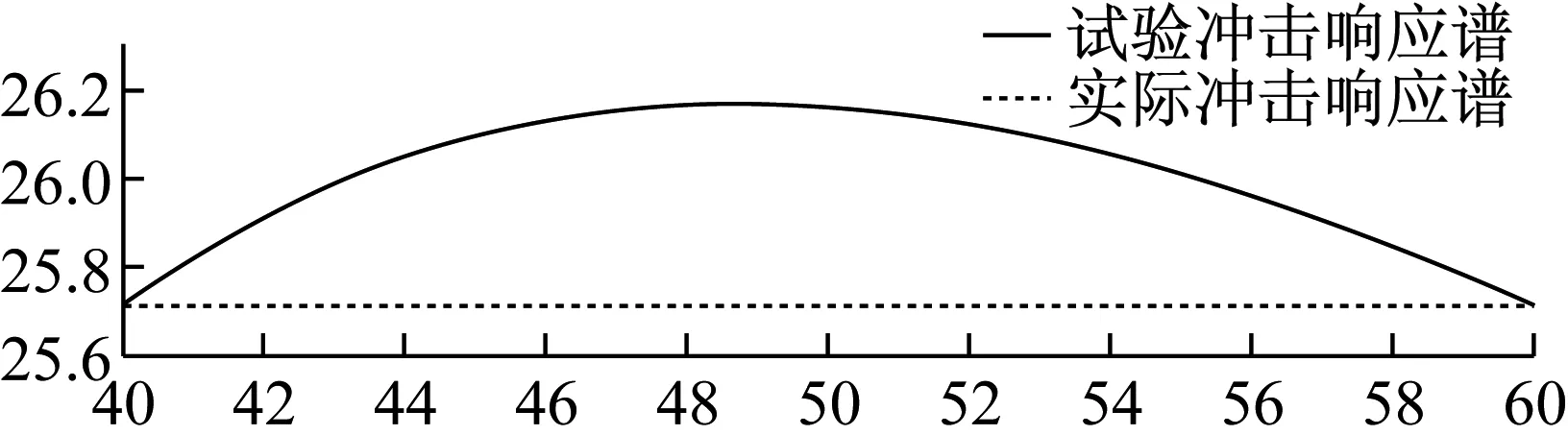
(a)x向试验/实验冲击响应谱

(b)y向试验/实验冲击响应谱

(c)z向试验/实验冲击响应谱

[1] 振动与冲击手册编写组.振动与冲击测试技术[C]//振动与冲击手册.北京：国防工业出版社，1990年.

[2] 董周战，秦庭森，李立名.空空导弹冲击试验及试验条件的确定[J].航空兵器，2001(3)：15-17.

DONG Zhouzhan, QIN Tingsen, LI Liming. Percussion experiment and institution of percussion experiment condition of air-to-air missile[J].Aero Weaponry, 2001(3)：15-17.

[3] 郭鹏.差分进化算法改进研究[D].天津：天津大学，2012年.

[4] 力学环境试验技术编写组.力学环境试验技术[M].西安：西北工业大学出版社，2003年.

[5] 赵玉刚.冲击响应分析方法及其应用[D].杭州：浙江大学，2004年.

[6] 任昌，潘宏侠. 基于冲击信号的冲击响应谱研究[J]. 火炮发射与控制学报,2010,21(2): 21-24.

REN Chang, PAN Hongxia. Study of shock response spectrum based on shocking signal[J]. Journal of Gun Launch & Control, 2010,21(2): 21-24.

[7] 王锡雄,秦朝烨,丁继锋,等.基于离散小波分解的火工冲击数据有效性分析与校正方法[J].振动与冲击, 2016, 35(14):1-6.

WANG Xixiong,QIN Zhaoye,DING Jifeng,et al.Validation and correction of pyroshock data based on discrete wavelet decomposition[J].Journal of Vibration and Shock,2016,35(14):1-6.

[8] 贺少华,吴新跃 . 一种多体系统冲击响应谱分析法[J]. 振动与冲击, 2011, 30(4): 127-130.

HE Shaohua,WU Xinyue. A shock response spectrum method of multi-body systems, 2011, 30(4): 127-130.

[9] 梁利华，荀盼盼，王保华. 基于ARMA模型的水下爆炸冲击谱预测[J]. 振动与冲击, 2013, 32(13): 23-26.

LIANG Lihua,XUN Panpan,WANG Baohua. Prediction of shock response spectrum of underwater explosion based on ARMA model, 2013, 32(13): 23-26.