航天器随机振动试验振动台驱动力估算方法

邓卫华，杨新峰，李艳辉，张玉梅

（航天东方红卫星有限公司，北京 100094）

0 引言

试验推力是振动试验设备的核心指标之一，足够的推力是振动试验顺利开展的基本条件，因此试验前对振动推力进行估算是必要的。文献[1]使用有限元建模分析的方法对某航天器振动试验推力进行估算，试验实测结果表明该方法对航天器正弦振动试验的估算误差为10%，能较好满足工程需要，但对随机振动试验的估算偏差较大。足够的经验数据能为推力估算提供帮助，但当新型号的航天器构型、质量等差异较大时，无法采用相似性类比的纯经验方法，因此需要寻求更科学、准确的估算方法。

准确计算航天器随机振动试验推力的主要困难在于结构在宽频随机振动环境下通常会产生复杂的动载荷，其值理论上是由从低频到高频的全频段所有振动贡献的综合。针对结构随机振动推力计算的研究一般都把推力计算转化为随机振动载荷识别问题。早在1954年，Miles就针对单自由度系统给出了白噪声激励下随机振动载荷近似等效为静态载荷的关系式，即著名的Miles公式[2]。但这种方法对于多模态的复杂结构是不适用的，于是有人在此基础上提出了模态质量参与法[3]，考虑到多自由度系统各模态对结构受载的贡献不同，在原公式中引入模态有效质量比作为权重系数。该方法概念清晰，简单易用，但在航天器上应用时需先解决2个问题：参与模态截止频率和非白噪声谱随机振动条件影响。前者决定了结构模态参与数量引起的误差，有研究基于应变等效的原则发现了应变的均方根值在频率远小于2000 Hz处就开始收敛，更有研究表明截止频率可取为400 Hz[4]。后者决定了试验输入量级引入的误差，但相关研究较少，往往被忽略不计。因此就航天器随机振动推力计算而言，采用当前的模态参与法仍会有较大误差。

本文基于模态参与的思想，针对截止频率和非均匀谱随机振动条件这2个主要误差因素，结合航天器随机振动的特征，对模态参与法进行改进和算法简化，并通过型号试验验证其可行性。

1 航天器随机振动试验基本特征

1.1 振动试验推力的构成

航天器振动试验一般在电动振动台上进行，振动台提供的推力Ft实际上需要支撑航天器、振动台运动组件（见图1）以及连接两者的夹具（见图2）3部分质量（mitem/mtable/mfix）的振动（Aitem/Atable/Afix），即

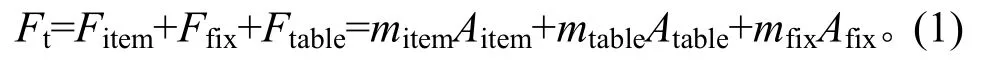
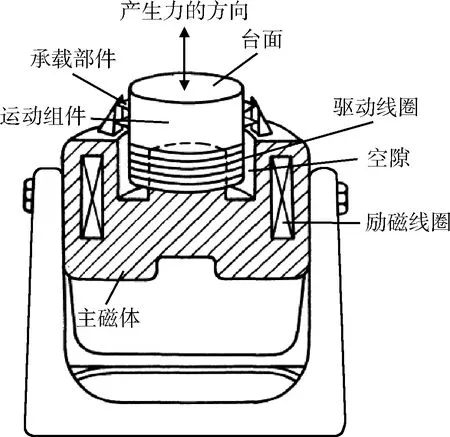
图1 电动振动台台体结构示意Fig.1 Sketch of the shaker structure

图2 航天器常用振动试验夹具Fig.2 The spacecraft vibration test fixture

根据电动振动台工作原理可知，其提供的推力Ft由激励电磁场强度B、驱动电圈电流I及其在磁场中的有效长度L决定[5]，即

对于某特定的振动台，B、L可视为常量，因此可由驱动电流I推算出振动推力Ft。工程上也常以监测驱动电流的变化来获得当时的振动台推力。

另外，工程实践也表明航天器振动试验推力根据振动方向的不同而有很大差异，一般可分为纵向振动与水平振动2种状态（见图3）或按3个轴向分别计算。

图3 航天器振动试验状态示意Fig.3 The spacecraft vibration test

1.2 航天器随机振动试验条件

试验推力的本质是要使航天器振动环境满足试验条件，因此Aitem/Atable/Afix都应与试验条件有关。航天器的试验条件谱线通常在全频段是不均匀的，而且需要在试验过程中根据航天器结构承受的振动载荷对原始试验条件进行下凹和响应限幅调整。试验推力的计算与试验条件相对应。图4给出了航天器典型随机振动的验收级条件曲线，纵向和横向振动的试验量级总均方根值分别为5.65grms和4.97grms。

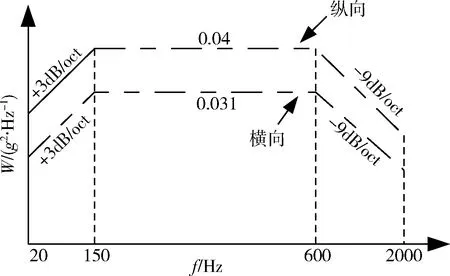
图4 航天器典型随机振动验收级条件曲线Fig.4 The typical spacecraft random vibration test condition curves

1.3 航天器振动试验动态特性

工程实践表明，相同的试验条件下，质量较小的航天器随机振动试验所需推力有时比质量较大航天器的更大。这与航天器各自独特而复杂的动态特性有关。因此计算航天器随机振动试验推力（关键是Aitem/Atable/Afix）必须考虑航天器自身的动态特性。这种特性与试验状态有关，不同方向也有明显差异。结构的振动特性通常用频率特性（或频率响应函数）H(f)来表示，对于单自由度阻尼系统[6]，

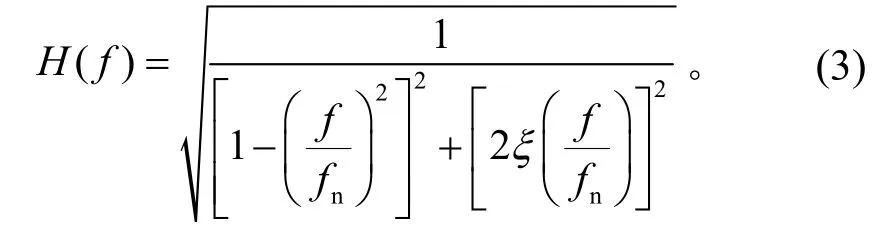
其中：f为激励频率；fn为系统固有频率；ξ为模态阻尼比。

对于类航天器等复杂结构系统，振动动态特性是多模态综合的结果，如何尽量准确地获得随机振动动态特性是决定试验推力计算结果准确性的关键。

2 模态参与法的改进与简化

2.1 模态参与法

模态参与法计算航天器随机振动载荷A的公式为

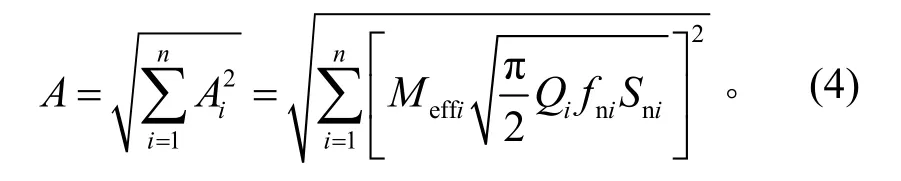
其中：Qi、fni、Meffi分别表示航天器第i阶模态的放大因子、固有频率、模态有效质量比；Sni表示随机振动试验条件谱在频率fni处的功率谱密度值。

模态参与法的计算过程为[7]：

1）用有限元法计算结构在截止频率内的各阶模态，以及对应的模态有效质量比Meffi；

2）从规定的试验条件加速度功率谱密度曲线中查出各阶固有频率对应的Sni；

3）确定各模态的放大因子，Qi=1/(2ξ)；

4）将以上数值代入公式(4)进行计算。

2.2 截止频率选取

综合分析多颗 500～1000 kg小卫星的随机振动试验数据，在其结构底部的应变测量值均方根，无论纵向或横向，一般在200 Hz以内就能达到全频段（20～2000 Hz）总均方根值的 95%以上；300 Hz处能达到99%（如图5所示）。这比NASA提出的截止频率[4]更低，从工程经验上可以认为截止频率一般不超过整星主要固有频率的2倍。

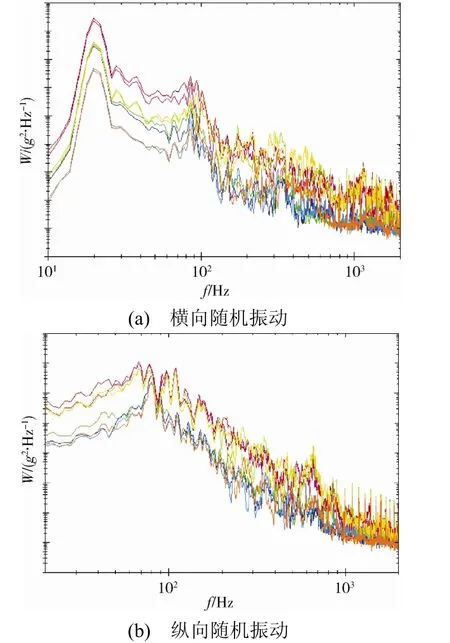
图5 某航天器结构底部随机振动应变测量功率谱密度曲线Fig.5 Strain PSD curves in random vibration test at the bottom of spacecraft structure

2.3 改进的随机振动载荷计算方法

模态参与法只考虑了随机振动条件在固有频率处对模态的影响，而忽略了非固有频率处对模态的影响。改进方法的随机振动载荷计算公式为

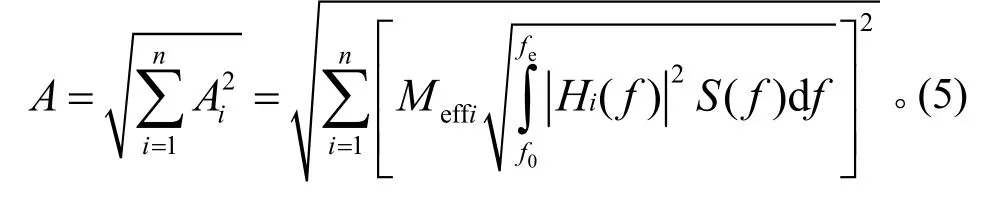
其中：S(f)为试验条件的功率谱密度函数；Hi(f)通过式(3)计算得到；f0、fe分别为计算的起始和截止频率。

相对于模态参与法，改进方法只需要将2.1节计算过程中第4）步的计算公式由式(4)换为式(5)即可。

2.4 改进法的工程经验简化

在工程中，作为试验条件的S(f)是一个分段的非均匀数列。根据Hi(f)的曲线特征（如图6所示），可以针对任意模态固有频率fni，将Hi(f)划分为 3个频段（即共振段、共振前段和共振后段）进行简化计算。

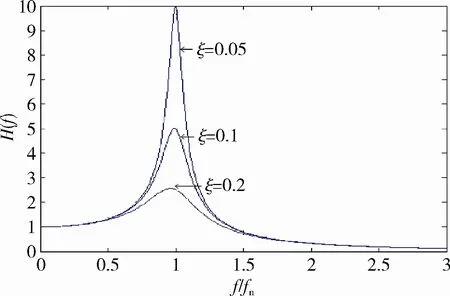
图6 单自由度阻尼系统频率特性曲线Fig.6 Frequency response characteristic curves of single DOF system

因此针对某个模态，其随机振动载荷贡献的算法可表示为

其中Ap、An、Aa分别表示共振前段、共振段和共振后段的加速度载荷。

Ap描述的是f＜fn频段。此时可以忽略模态阻尼的作用，由式(5)推得

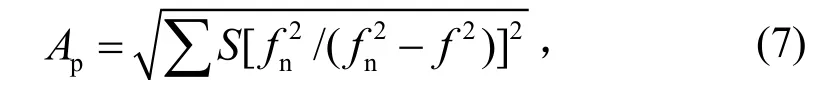
并可取计算频率范围为f0～0.92fn。

An描述的是f≈fn频段。该频段的加速度载荷值很大程度上取决于放大因子Q和计算带宽Δf。可依工程经验取Δf=0.16fn，在阻尼比较小的情况下可采用三角面积方法得到An的计算公式，

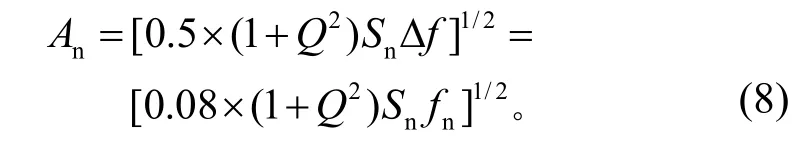
Aa描述的是f＞fn频段。此时也可以忽略模态阻尼的作用，得到

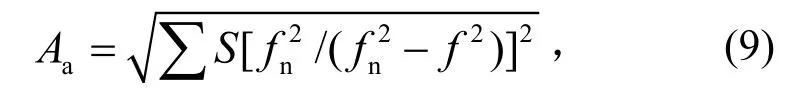
并可取计算频率范围为1.08fn～2fn或1.08fn～整星随机振动载荷截止频率。

2.5 改进法及其简化法的验证

首先针对单自由度系统，以100、200、300、400、500 Hz共5个不同主频率，分别在0.04g2/Hz均匀输入加速度谱（白噪声）振动条件为例，将采用改进法及其简化法（即三频段）计算得到的结果与采用模态参与法（即采用Miles公式）计算得到的结果进行比较（见表 1）。其中：三频段计算公式中频率最低取为1 Hz，最高为2000 Hz，放大因子Q=10；相对偏差是指各方法计算结果与模态参与法计算结果比较后的偏差。由表1可以看到：改进法与模态参与法的计算结果吻合；简化法与模态参与法的计算结果接近，偏差小于5%。可见，用这2种方法估算单自由度（或单一主模态结构）系统的随机振动加速度载荷是有效的。

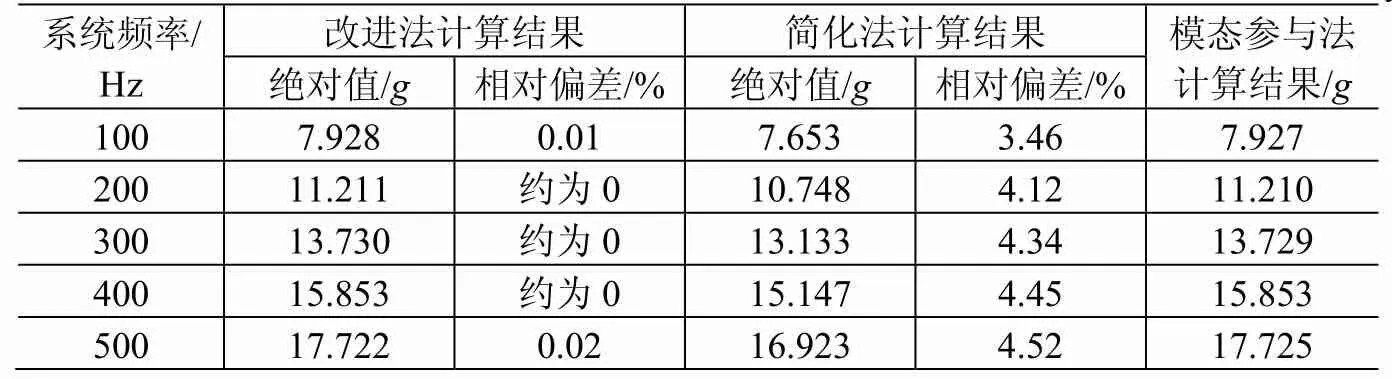
表1 改进法及其简化法与模态参与法对单自由度系统的计算结果对比Table 1 Comparisons between the improvement method and the Miles method for single DOF system

对于多自由度系统，以文献[8]中的三自由度弹簧-质量系统为例，系统的3个质量为m1=200 kg、m2=250 kg、m3=300 kg，3个弹簧刚度为k1=108 N/m、k2=2×108 N/m、k3=3×108 N/m。此系统受宽频带均匀基础激励，激励加速度谱S=0.01g2/Hz，放大因子Q=10。进行多模态分析，得到三阶模态频率分别为fn1=69.6 Hz、fn2=153.8 Hz、fn3=238.3 Hz，三阶模态质量比分别为Meff1=0.803、Meff2=0.149、Meff3=0.048，系统加速度载荷力为20 377 N。利用前述 3种方法进行计算，得到加速度载荷分别为2.770g（改进法）、2.686g（简化法）和2.778g（模态参与法），载荷力为加速度载荷与总质量750 kg的乘积（结果如表2所示）。相对于文献中结果，各方法的计算偏差均小于5%，其中改进法的偏差最小（小于0.1%）。这验证了改进法及其简化的三频段方法计算多模态结构加速度载荷的可行性。

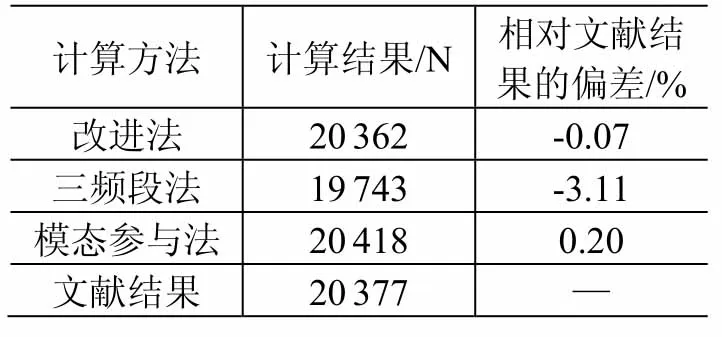
表2 改进法及其简化法与模态参与法对多自由度系统的计算结果对比Table 2 Comparisons between the improvement method and the Miles method for multi-DOFs system

3 工程应用实例

某航天器总质量mitem=1050 kg，纵向随机振动条件如图 7所示，试验量级的总均方根值为7.36grms。按照公式(1)，推力由航天器、台体活动部件以及夹具3部分构成（即Fitem/Ftable/Ffix）。由于是非白噪声激励，不能采用模态参与法计算Fitem，所以采用改进法：首先分析得到纵向前二阶固有频率为fn1=72.5 Hz、fn2=81.3 Hz，前二阶模态质量比为Meff1=31.52%、Meff2=37.59%，其他模态质量比很低，可以忽略；再利用三频段简化方法得到等效加速度为2.720 1g，则单独卫星的纵向随机振动所需推力约为2 856.1 kgf。（本节为方便计算，采用kgf作为推力单位，1 kgf=9.807 N）。纵向振动时，台体和夹具可视为刚体运动，故输入均方根加速度都为 7.36g；而台体与夹具的质量分别为mtable=149 kg、mfix=205 kg，则纵向台体与夹具需要的推力为(149+205)×7.36=2 605.4 kgf。因此，航天器纵向振动所需的总推力为5 461.5 kgf。试验中根据振动台驱动电圈电流I获得的推力为5 605.2 kgf，说明估算的推力与实际推力非常接近。

横向随机振动时，试验条件如图8所示，试验量级的总均方根值为 6.53grms。该状态下，卫星与夹具作为一体按弹性体考虑。分析得到主要模态：一阶频率 22 Hz，模态质量比 58.8%；二阶频率85 Hz，模态质量比 19.5%；忽略其他模态。计算得到等效加速度为1.493 7g，卫星与夹具一体的质量为1250 kg，因此组合体横向随机振动所需的推力约为1867 kgf。台体活动部分在横向振动时增加了水平滑台等部件，总质量增加到614 kg，台体可按刚体运动，按输入均方根加速度计算，台体需要的推力为614×5.6=3438 kgf。因此，航天器横向（y向）振动所需的总推力为1867+3438=5305 kgf。试验中根据振动台驱动电圈电流I获得的推力为4989 kgf，也与计算结果接近。

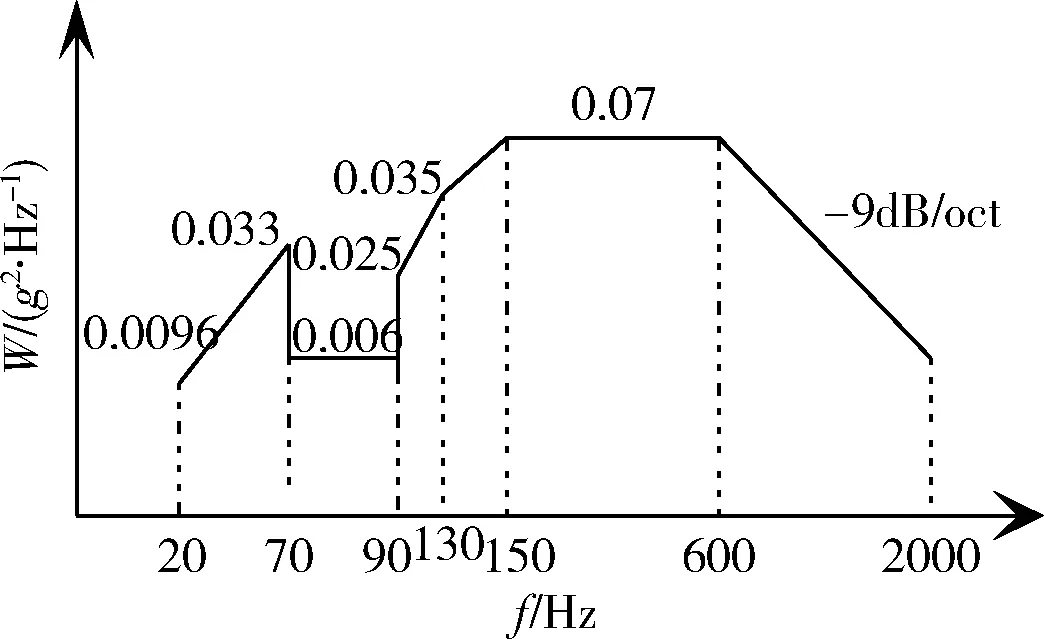
图7 某航天器纵向随机振动试验条件曲线Fig.7 The vertical random vibration test condition curve for a spacecraft

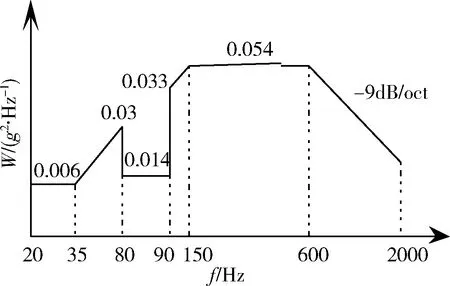
图8 某航天器横向随机振动试验条件Fig.8 The horizontal random vibration test condition curve for a spacecraft

4 结束语

本文提出了对模态参与法的改进方法，经验证可以用来更准确地计算非白噪声激励的随机振动载荷，其工程简化方法在实践中体现了简单易用的特点。使用改进方法可以在航天器随机振动试验实施前就展开试验推力的估算，评估振动试验设备能否满足试验需要。在工程中，还可以在总结经验规律的基础上进一步简化使用三频段法，快速获得满足工程需求的评估结果。

（References）

[1]李艳辉,邓卫华,王晓耕.卫星振动试验中推力的估算方法[J].航天器环境工程,2013,30(2): 160-164 LI Y H,DENG W H,WANG X G.The thrust evaluation for satellite vibration test[J].Spacecraft Environment Engineering,2013,30(2): 160-164

[2]MILES J W.On structural fatigue under random loading[J].Journal of Aerospace Science,1954,21(11):753-762

[3]Payload flight equipment requirements and guidelines for safety-critical structures: SSP52005B[S],1998

[4]George C Marshall Space Flight Center.Design and verification guidelines for vibroacoustic and transient environments: NASA TM-86538[R],1986

[5]柯受全.卫星环境工程和模拟试验[M].北京: 宇航出版社,1996: 34-49

[6]朱石坚,楼京俊,何其伟,等.振动理论与隔振技术[M].北京: 国防工业出版社,2008: 1-19

[7]杨宝宁.随机振动条件下设计载荷的确定[J].航天器工程,2006,15(3): 33-37 YANG B N.Engineering methods for determining quasi-static limit load for structures under random vibration[J].Spacecraft Engineering,2006,15(3): 33-37

[8]WIJKER J.Random vibrations in spacecraft structures design[M].New York: Springer,2009