基于正交试验设计的正交异性钢桥面系多因素优化研究

2018-02-26王柏文

西安建筑科技大学学报（自然科学版） 2018年6期

王柏文，唐焱，刘扬，王龙

(1.长沙理工大学土木工程学院，湖南长沙410114；2.中冶长天国际工程有限责任公司市政建筑工程公司，湖南长沙410205)

正交异性钢桥面板具有质轻、高强、易施工等优点，近年来被广泛应用于国内外大跨桥梁建设中.桥面铺装作为钢桥面板的保护层和荷载扩散层，在改善行车舒适性和安全性的同时，对钢桥面板耐久性也有重要意义.现有钢桥面系铺装层的一些病害问题较为突出，主要表现在纵横向裂缝破坏和铺装层与钢桥面间脱层[1-7].由于钢桥面板与铺装层间存在复合作用，铺装层的存在有效地降低了桥面板细节的疲劳应力，同时，由于正交异性板复杂的结构形式及显著的荷载局部效应，其构造参数对铺装层的应力场分布有着重要影响.桥面板与铺装层互相影响、共同受力，桥面铺装设计应与主梁设计同步、协调进行，以保证桥梁结构具有足够的刚度.为解决钢箱梁桥面铺装破坏的问题，国内外学者已进行了大量研究，黄成造[8-9]等研究了构造参数对铺装层应力的影响，提出在钢箱梁顶板纵向加劲肋之间加设横向加劲小肋的办法用以改善铺装层的受力状况，最终指导了珠江黄埔大桥钢箱梁桥面铺装层的设计.林广平[10]等基于BP神经网络模型，对钢桥面铺装体系构造参数进行了优化设计.明图章[11]等将钢桥面板与铺装层的性能要求结合在一起，以铺装体系造价和铺装层表面极限应力最小化为目标，进行了多目标优化设计.

以往的研究虽然取得了令人满意的结果，但也存在以下不足：1)未能明确正交异性板结构参数及铺装层材料与结构参数对铺装层力学特性影响的大小顺序；2)在对正交异性钢桥面系进行优化设计时，如何能以较少的计算成本取得良好的优化结果.

本文以某大跨悬索桥钢箱梁为研究对象，建立精细化的局部钢桥面系有限元子模型，将正交异性钢桥面板和铺装层作为整体进行分析，计算轮载作用下铺装层的应力分布状况并确定最不利轮载位置.通过正交试验设计方法，研究正交异性板结构参数及铺装层材料与结构参数对铺装层力学特性的影响.以桥面铺装体系质量最轻及铺装层内横向拉应力最小两类指标构造目标函数，通过建立变量间的响应面近似模型，对正交异性钢桥面系进行优化设计分析，以期为今后的正交异性钢桥面系设计提供借鉴与指导.

1 局部正交异性钢桥面系有限元分析

1.1 工程概况

国内某大跨悬索桥，主缆分跨192+820+176m，主梁采用钢箱梁形式，桥轴中心线处梁高3 m，宽29.78 m(不含风嘴)，桥面横坡2%；全桥共划分65个标准梁段，长度为12.8 m，内设4道横隔板，横隔板间距为3.2 m，厚度为10 mm；桥面铺装层为67 mm (35 mm改性沥青玛蹄脂碎石SMA-10+30mm浇筑式沥青砼GA-10+2mm钢桥面防水粘结层).钢箱梁桥面板采用正交异性板，主要组成构件的具体尺寸分别见表1所示.

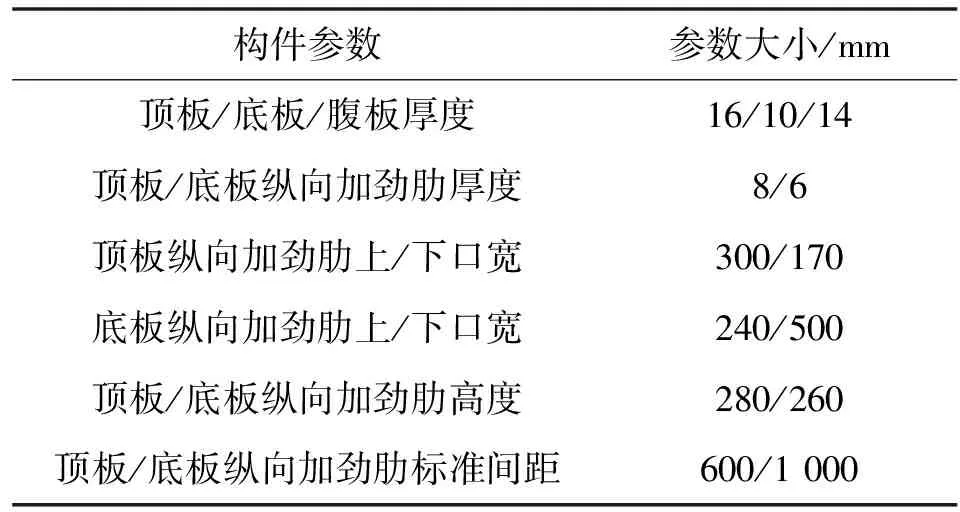
表1 钢箱梁主要构造参数

1.2 局部钢桥面系有限元模型

在用有限元方法对钢箱梁桥面铺装体系分析时，采用简化的局部子模型由于对用户和计算机要求不高而被广泛采用.为了保证选用的局部模型能反映结构实际的受力状态，同时提高计算精度、减少计算成本.文献[12]～[13]利用子模型技术和综合评价方法对局部钢桥面系模型几何尺寸与边界约束条件进行了优化，对比分析表明简化子模型具有较高的计算精度.文献[14]完成了局部子模型的参数优化分析，对某工程实桥进行测试，将采用优化的局部子模型分析得到的计算值与实桥加载得出的实测值对比，结果表明计算值与实测值差别不大，优化的局部子模型可作为钢桥面铺装计算模型使用.

基于上述研究成果，本文采用通用有限元分析软件Workbench建立了精细化的局部钢桥面系有限元子模型，模型初始构造参数均与原桥一致.模型纵向为三跨，横向有7个U肋，横隔板高1.2 m，正交异性板采用板壳单元Shell181模拟，弹性模量210 GPa，泊松比0.3；不单独建立钢桥面防水粘结层，另外两铺装层简化为材料一致的单层等厚铺装层，铺装层沥青混凝土采用solid186单元模拟，假定为各向同性且连续的完全弹性体，其模量与温度及材料密切相关，参考文献[8]取弹性模量为3 000 MPa，泊松比0.25.铺装层与钢桥面板之间采用Bonded接触，不考虑桥面板与铺装层间的黏结滑移效应.另外，由于铺装层的施工通常是在正交异性钢桥面板完全施工结束后才进行铺筑，因此在计算中可不考虑钢桥及铺装层自重[12-13].建立的有限元模型单元总数为68 761，节点总数为178 286，如图1所示.

图1 有限元计算模型Fig.1 Finite element model

1.3 计算结果分析

计算荷载按《公路桥涵设计通用规范》(JTG D60-2015)取公路-Ⅰ级550 kN车辆荷载后轴一侧车轮，单轮重70 kN，着地面积为0.6 m×0.2 m，考虑冲击系数和车辆超载的影响后轮压取0.7 MPa.模型边界条件设置为纵边自由，横边两侧为简支约束，横隔板底端固结.荷载纵向布置在第二跨跨中截面处，沿桥面横向布置了3个荷载作用位置，如图2所示：荷位1为车载施加于两U肋中心之间正上方；荷位2为车载以U肋一肋边为中心对称施加于正上方；荷位3为车载对称施加于U肋正上方.

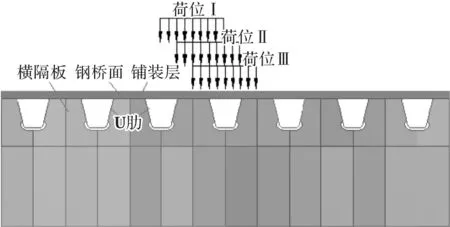
图2 荷载横向布置示意图Fig.2 Load diagram of transversal arrangement

计算结果表明：(1) 钢桥面铺装层荷载局部效应显著，建立的局部钢桥面系有限元子模型分析结果与文献[8]中的结论一致；(2)以铺装层横向拉应力或挠跨比为控制指标时，横桥向最不利荷位是荷位3，铺装层最大横向拉应力出现在荷载作用区边缘外加劲肋肋顶处.图3给出了轮载作用在最不利荷位3时，钢桥面铺装层纵横向拉应力、层间剪应力及弯沉值分布状况.

图3 荷载效应Fig.3 Load effect analysis

2 参数敏感性分析

2.1 正交试验设计法

正交试验法是一种对多因素多水平进行有效研究和处理的设计方法，根据正交性从全面试验中挑选出部分具有代表性的点进行试验，这些点具有“均匀分散，齐整可比”的特点[16-17].与全面试验相比，采用正交试验法，在保证试验结果可靠和结论正确的前提下，尽可能的减少了试验次数，因而在各学科领域应用广泛.近年来在土木工程领域也常见基于正交试验法的研究成果，如贾超[16]等基于正交试验设计对层状盐岩地下储库群进行了多因素优化研究.付宏渊[17]等运用正交试验法对岩质边坡进行了动力稳定性分析.

试验设计一般有以下几个步骤：(1)试验方案设计；(2)按照方案进行试验获得试验结果；(3)对记录的试验结果进行数据分析；(4)对结果进行试验验证.

2.2 数值模型与计算参数

引言部分介绍了铺装层破坏常见形式及原因，从实际安全角度出发，本文分别以铺装层最大横向拉应力δmax、层间最大剪应力τmax及铺装层最大弯沉值hmax为评价指标，旨在通过正交试验设计，利用数值模拟软件完成分析，明确影响因素对各评价指标的影响程度，通过合理的参数设计降低三种评价指标数值，以提高铺装层寿命，同时为今后同类桥梁结构铺装提供借鉴与指导.

对上述正交异性钢桥面系进行优化研究时，在已有的研究成果之上，结合《公路桥涵设计通用规范》(JTG D60-2015)主要构件的设计要求，按上节确定的最不利轮载方式加载，考虑了轮载作用下铺装层厚度、铺装层沥青混凝土弹性模量、钢桥面板厚度3个因素对钢桥面系力学特性的影响，每种因素分别选择3种不同的水平，如表2所示.

在确定了试验因素及其参数水平之后，选择一张合适的正交表至关重要，它不仅决定了整个数值模拟试验过程的进行，同时对结果的处理也有重要影响.本文拟选用L9(34)正交表，式中：“9”为正交表行数(试验数)，“4”是列数，表示在此正交数值模拟试验中最多可安排的因子个数，本次数值模拟试验共3个因子，故多余一列为空列，“3”表示试验中各因素的水平数.正交表设计与计算结果如表3所示.

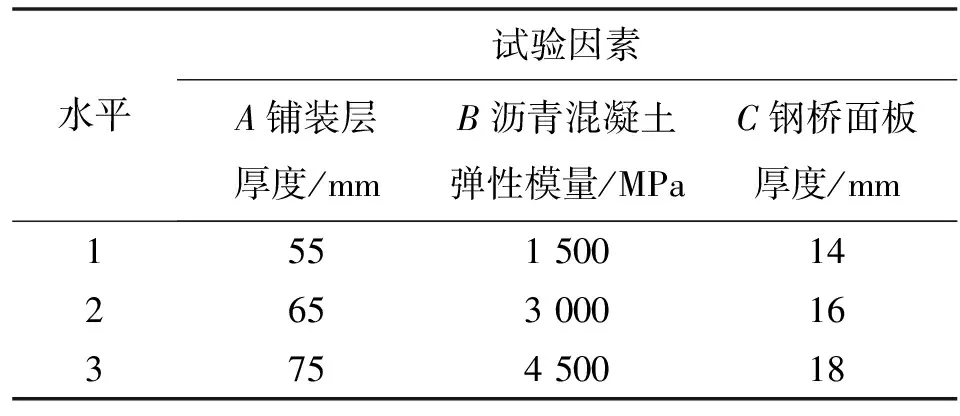
表2 影响因素及水平

2.3 数值计算结果分析

对数值模拟试验结果进行处理的目的在于确定试验因素对评价指标影响程度的主次顺序、各因素最优水平及试验范围内不同因素不同水平的最优组合.根据正交试验表的综合可比性，采用极差分析法(R)法可以直观快速的对试验结果进行分析，确定试验因素主次及最优组合.表4给出了对3种评价指标进行极差分析的结果，同时为了能够更直观地看出各因素水平变化时，各评价指标的波动情况，绘出因子和指标的关系如图4所示.

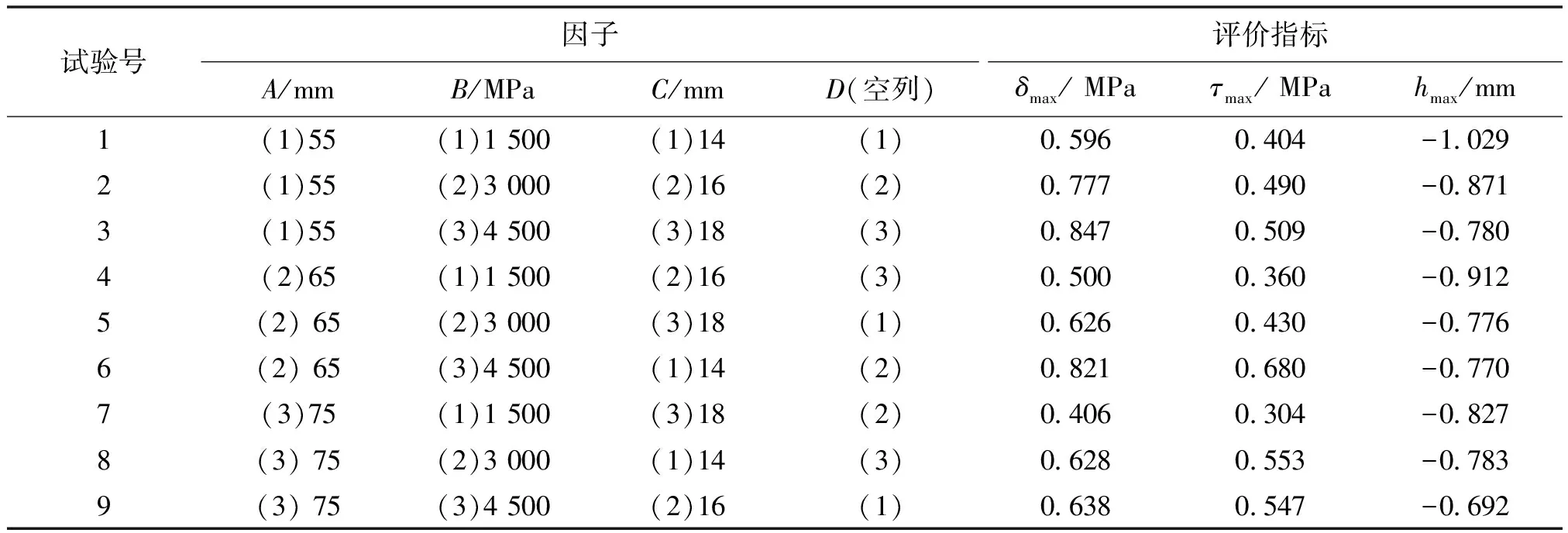
表3 L9(34)正交数值模拟试验设计

表4 极差分析

注：以最大横向拉应力δmax为评价指标为例，安排A因子的第1列时，记相应第i个试验号的结果为yi，第1列的k1就是对应于该列中“1”水平的3个试验结果数值相加后取平均值，同样方法分别计算k2、k3，R=kmax-kmin.如在第1列中：k1=(y1+y2+y3)/3=(0.596+0.777+0.847)/3=740×e-3，k2=649×e-3，k3=557×e-3，R=kmax-kmin=k1-k3=740×e-3-557×e-3=183×e-3.

从表4可以看出，采用3种不同的评价指标时，铺装层弹性模量B的极差R均大于铺装层厚度A及钢桥面板厚度C的极差R，说明铺装层弹性模量B是它们最显著的影响因素，铺装层弹性模量的改变对钢桥面系结构各方面力学性能都具有很大的影响.对于铺装层内最大横向拉应力，钢桥面板厚度变化时的极差R=56×e-3为最小，说明其对最大横向拉应力影响最弱，以降低横向拉应力为目标时，根据不同因素不同水平计算出的ki，列于表4，当因素ABC分别取水平3、水平1、水平3时，k指标分别是557×e-3、501×e-3、626×e-3，分别为不同因素各水平ki的最小值.因此可确定此时因素的最佳水平为A3B1C3；同理，对于铺装层与钢桥面板间最大剪应力，铺装层厚度对其影响最弱，以减小层间剪应力为目标，其因素的最佳水平为A1B1C3；对于铺装层最大弯沉值，钢桥面板厚度对其影响最弱，为保证安全需尽量减小铺装层弯沉值，因素的最佳水平为A3B3C3.

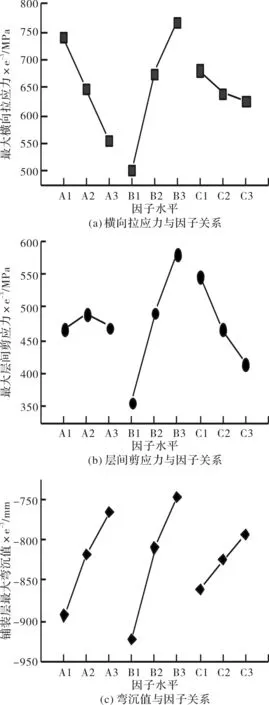
图4 指标与因子关系Fig.4 Relationship of target with factors

从图4可以看出，随着铺装层厚度的增加，铺装层内最大横向拉应力及铺装层最大弯沉值均有所减小，而铺装层与钢桥面间的最大剪应力变化不是很明显，铺装层厚度在逐渐增加的同时，层间剪应力先逐渐增加后慢慢减小；在铺装层的弹性模量逐渐增加的过程中，虽然铺装层的最大弯沉值在逐渐减小，但是铺装层内的最大横向拉应力及最大层间剪应力反而在逐渐变大；钢桥面板厚度逐渐增加的过程中，3个评价指标均有所降低，但效果并不明显.

钢桥面铺装层的破坏形式是多样的，其背后的原因也不尽相同，所以在进行钢桥面铺装设计时，应考虑多方面因素.若仅以一个参数为控制指标，往往会导致不合理的设计，造成顾此失彼的现象，最终降低了铺装层的寿命，也增加了后期维修加固的费用.具体到本次正交试验设计，若仅以铺装层内最大横向拉应力为控制指标，根据表4或图4可知，当铺装层内最大横向拉应力最小时，因素A的最优水平为水平3，因素B的最优水平为水平1，因素C的最优水平为水平3，故因素的最优组合为A3B1C3，但是我们可以发现，最优组合中B因子若取水平“1”，此时铺装层的弯沉值又会最大，这与我们想要达到的多目标最优并不一致.同样的，仅以其他两个参数分别为单一的控制指标时，也会面对同样的问题.基于正交试验设计进行多目标优化时，往往会由于评价指标间的矛盾性，带来方案的不可比较性，这使得在寻找满意方案的试验过程中会遇到困难；另外，基于正交试验的优化研究所确认的仅仅是因子的最优组合，组合的因子水平与最初设计有关，无法准确确定各因子最优取值.可以利用响应面法进行优化设计解决上述问题，本文将在下节做出详细介绍.

3 基于响应面法的多目标优化设计

响应面法(RSM)是以试验设计(DOE)为基础的用于处理多变量问题建模与分析的一套统计处理技术，其原理是当某点周围部分数量点的实际函数值已知时，通过某种方式利用这些已知点建立一个超曲面，将隐函数显化，在充分靠近这个点的区域内，可用这个近似曲面替代实际函数进行计算.响应面模型包含了前述正交试验设计点，克服了正交试验无法准确确定各因子最优取值的问题.基于响应面法的优化设计是结构优化设计上的一次质的飞跃，与传统的优化设计方法相比，它解决了传统优化过程中的繁重的迭代次数问题，大大提高了优化设计的效率[18].RSM方法的主要步骤如下：(1) 确定优化设计变量和目标函数；(2)制定DOE方案并完成试验设计；(3) 利用完成的试验设计点通过回归分析，建立响应面模型；(4)基于建立的响应面模型完成优化设计，并检验优化结果是否满足要求.

3.1 优化变量及目标函数

优化设计的目的通常体现在结构满足力学性能与功能要求的前提下，材料使用最少，结构质量最轻，达到经济最优的效果；同时，考虑到钢桥面铺装层破坏主要是纵横向裂缝破坏，前两节计算结果也表明，最不利轮载作用下，铺装层内横向拉应力比纵向拉应力要大.因此，本文将铺装层内最大横向拉应力δmax及钢桥面系的质量M作为两个优化目标，目标函数为：minG=d1minδmax+d1minM式中：d1、d2为权重系数，用来描述各目标函数的重要程度，这里d1、d2分别取0.3和0.7，主要基于以下几点：(1)单纯的以横向拉应力最小或结构质量最轻为目标，优化效果往往不够理想；(2)在保证横向拉应力处于安全范围的前提下尽可能减轻结构自重，降低工程造价.

在结构优化设计的过程中，需要优选参数作为优化设计中的设计变量，对优化目标影响较小的参数往往可以保持原设计值不变.由上节计算结果可以看出，最不利轮载作用下，铺装层厚度的变化及铺装层弹性模量的改变对铺装层内最大横向拉应力影响较大，设计规范给出了铺装层厚度可在30～80 mm之间，将铺装层厚度A及沥青混凝土弹性模量B作为设计变量，考虑到计算规模及响应面拟合精度要求，优化范围为在原设计值基础上变动±10%；钢桥面板厚度变化时，铺装层内最大横向拉应力变化不是很明显，且从施工及安全角度出发，钢桥面板厚度变化范围有限，因此可不将其作为设计变量.

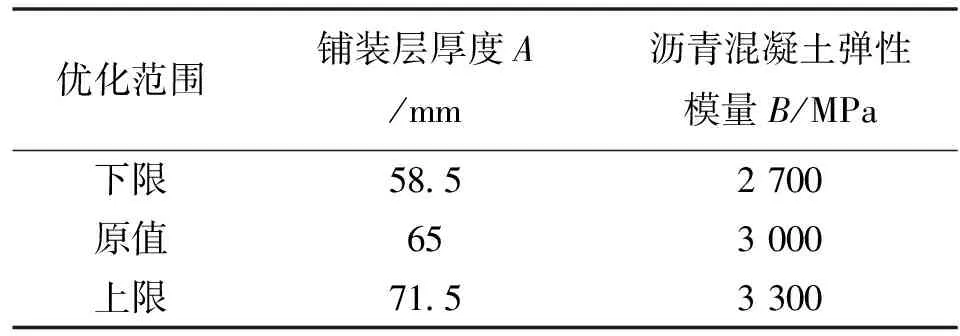
表5 设计变量取值

钢桥面铺装结构由正交异性钢桥面板与铺装层组合而成，在服役过程中的使用性能应满足要求.为防止铺装层与钢桥面板间发生铺装层剪切滑动破坏，最不利轮载作用下，最大层间剪应力τmax不得超过容许剪应力值[τ]容许，参考以往研究成果，[τ]容许取0.5 MPa[6].由于钢桥面系显著的荷载局部效应，荷载作用下，钢桥面板铺装层表面会形成高应力区域，局部挠度随之增加，降低了铺装层的抗裂性能.设计规范采用铺装层的局部挠跨比表征铺装层与正交异性钢桥面板的变形性能，最不利轮载作用下，局部挠跨比d/lmax不得超过容许值[d/lmax]容许，按规范[d/lmax]容许取1/1 000.

3.2 响应面模型建立

Workbench中运用模块Design Exploration，根据上节给出的设计变量取值范围，采用CCD法(中心复合设计)完成了两因素五水平设计，总共17次试验，基于Genetic Aggregation原则拟合得到设计变量与约束变量和目标变量间的响应面模型，拟合的相关系数平方(R2)均大于0.99，验证了响应面模型的准确性.图5给出了部分响应面模型.

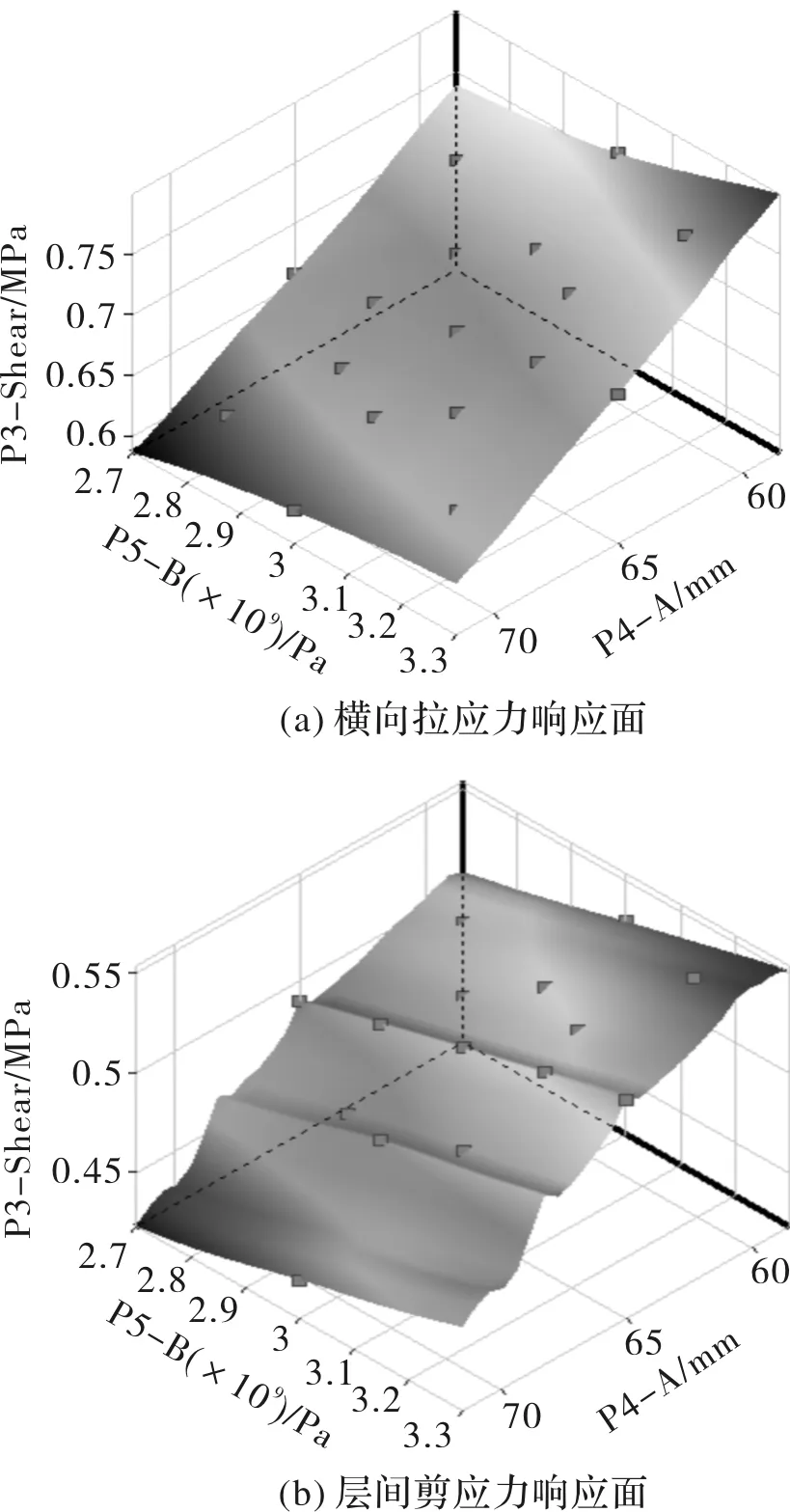
图5 变量间响应模型Fig.5 Response surface model between variables

3.2 优化设计及有限元验证

以上述拟合的响应面模型为基础，采用筛选法对试验模型进行优化设计，此方法是从1组给定的样本(设计点)中按照响应面模型得出最佳设计点，其优化精度与样本数量选取有关.本文将样本点设为10 000，在满足状态变量要求的前提下，按照优化设定目标，产生了三组候选的优化设计点，如表6所示.综合评价后选用第一候选设计点，其层间剪应力及挠跨比约束条件均满足要求，优化后的铺装层横向拉应力较原设计降低了0.99%，质量较原设计减小了2.12%.同时为了验证设计优化结论的准确性，按照候选设计点1的结构尺寸进行仿真分析，表7列出了优化前、基于响应面法优化及按照优化点仿真的计算结果对比.从表7结果可以看出优化结果与仿真结果误差较小，优化结果满足要求.由于本文仅针对局部子模型进行优化，同时优化考虑的因素有限，优化效果并不十分显著.若将此优化方法推广到整个桥面系中，同时考虑更多因素的影响，定会取得很好的优化效果，这将是下阶段要进行的主要工作.