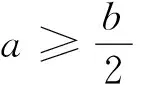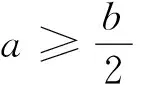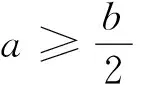梯形中平行四边形的面积最大问题
2018-02-26四川内江师范学院数学与信息科学学院
四川内江师范学院数学与信息科学学院
余小芬 刘成龙 (邮编:641100)
1 问题

图1
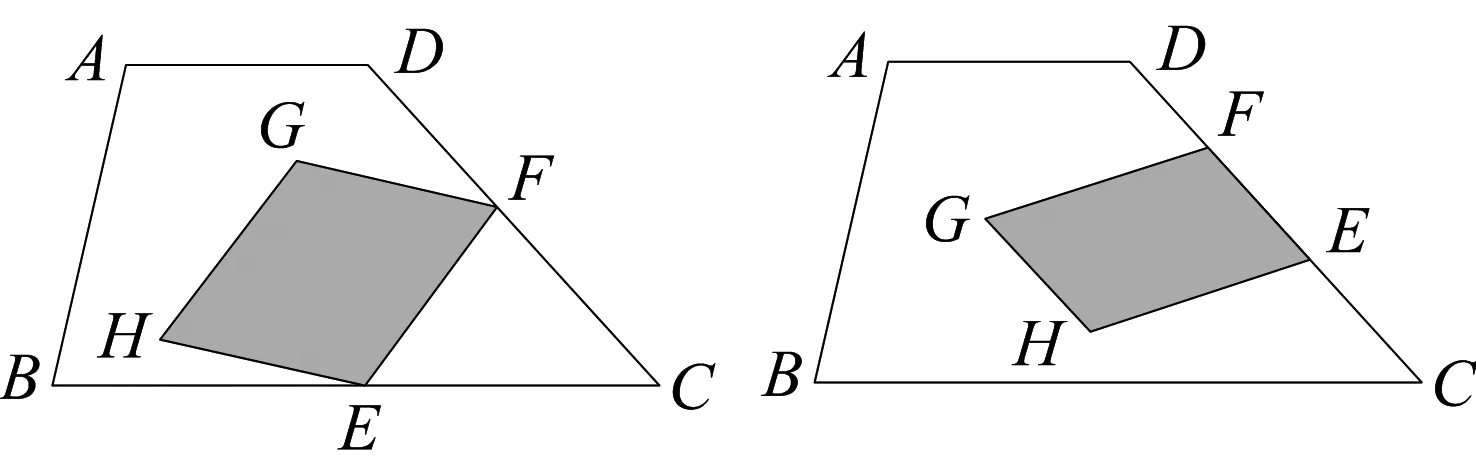
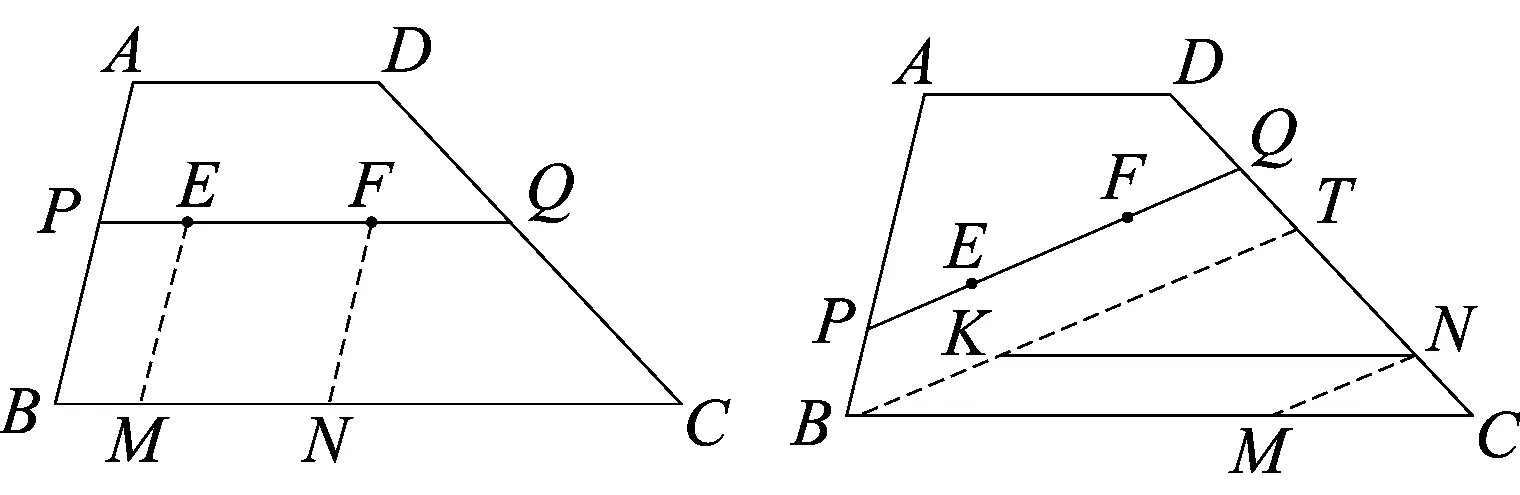
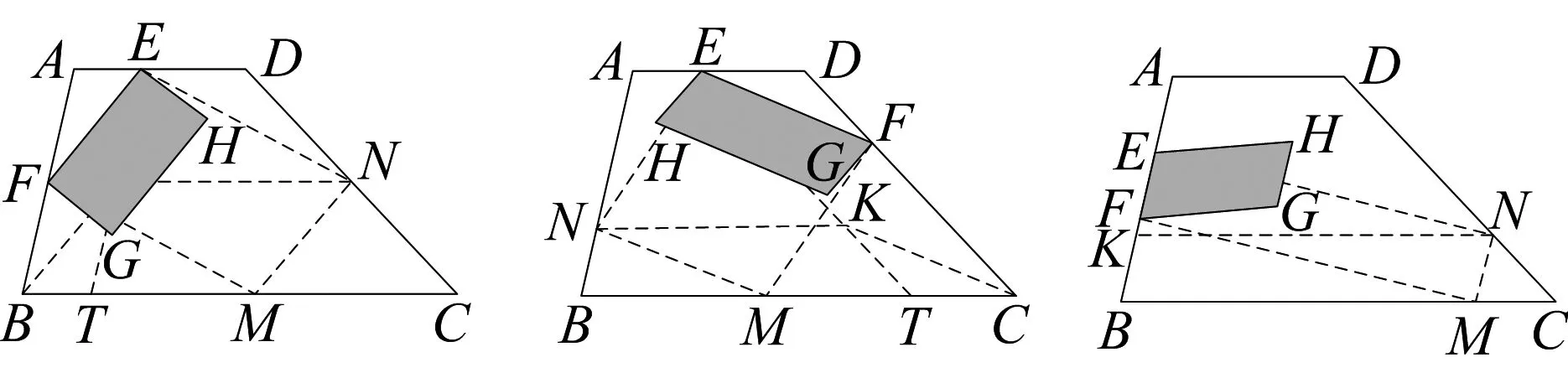
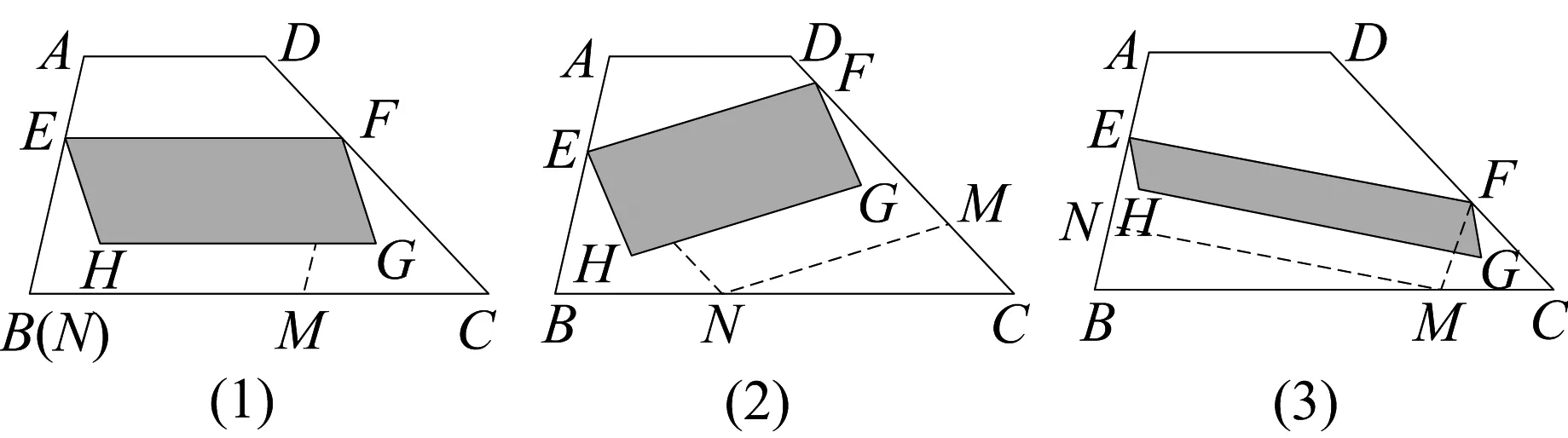
问题如图1,梯形ABCD中,AD//BC,AD=a,BC=b(a 引理1在梯形ABCD内任作EFGH,则EFGH至少有一边(不妨记为边EF)满足以下位置关系之一: (1)点E、F都落在梯形ABCD的边上; (2)点E、F不全落在梯形ABCD的边上.此时,总存在梯形边上的两点M、N,使得MNEF. 引理1的说明: (1)点E、F都落在梯形ABCD的边上,有以下情形(图2~图11): 图2 图3 图4 图5 图6 图7 图8 图9 图10 图11 (2)点E、F不全落在梯形ABCD的边上.此时,EF所在直线与梯形ABCD的边相交于P,Q两点(P、E重合与Q、F重合不同时成立),有以下情形(图12~图17): 图12 图13(1) 图13(2) 图13(3) 图14 图15 图16(1) 图16(2) 图16(3) 图17 特别要指出的是,图12~图17中,若构造出的MN恰好和EFGH的边GH重合,则可归结为引理1(1)的情形;若GH夹在EF和MN之间,则EFGH可扩大为EFMN;若EF夹在GH和MN之间,则EFGH可扩大为MNGH. 因此,按上述扩大方式,引理1(2)中扩大后的平行四边形都可归结为引理1(1)中情形.所以只需讨论引理1(1)中各类平行四边形面积的最大值即可. 下面依次给出图3,图5,图6,图7,图8,图10,图11对应扩张后的最大面积平行四边形的作法(由于图2,图4,图9情形简单,此处略). 观察图18~图24,不难得出梯形中面积最大的平行四边形的特征为:平行四边形的四个顶点全都落在梯形的边上. 图18 图19 图20 图21 图22 图23 图24 图25 引理2如图25,梯形ABCD中,AD//BC,AD=a,BC=b(a 证明如图25,过F作AB的垂线交AB(或AB延长线)于点N,过C作AB的垂线交AB(或AB延长线)于点K,过G作BC的垂线交BC(或BC延长线)于点P,交AD的延长线(或AD)于点Q. 下面给出梯形中平行四边形最大面积的结论. 图26 定理如图26,梯形ABCD中,AD//BC,AD=a,BC=b(a 证明如图26,延长EF与CB的延长线交于点K.设EFGH的边EF=s,EF边上的高为l,AE=m,AF=n,则ED=a-m,FB=c-n,其中0≤m≤a,0≤n≤c(特别指出,当不等式中的m或n取等号时,对应EFGH的顶点位置较为特殊.例如:当m=0时,点A、E重合,此时边EF落在梯形边AB上). 令f(n)=-(b-a)n2+(bc-2mc)n+mc2,其中0≤n≤c. 至此,本文开始提出的问题得到解决.2 对梯形中面积最大的平行四边形的特征分析

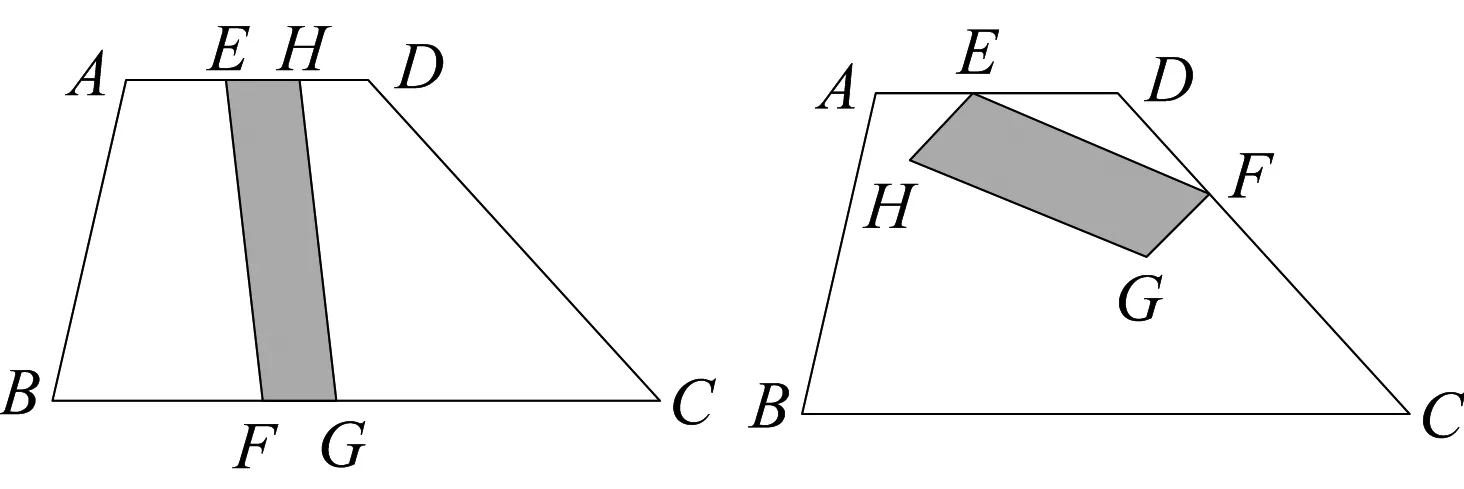








3 梯形中平行四边形最大面积的结论