高三复习课教学的一点尝试与思考

西安电子科技大学附属中学

汪贵宏 (邮编：638400)

1 提出问题

笔者参加了我区多个学校的高三教研活动，听了不少准备很充分的教学公开课和平时的自然课堂，通过听课、交流与反思，发现高三复习课教学效率低下现象较为普遍：先让学生板演，进而老师或者学生进行点评，指出解答中的问题；或者先让学生讲解题思路，师生一起求解.这样的教学模式，往往使成绩好的学生仅满足于最终答案的正确与否，不再关注问题的本质规律；成绩相对弱的学生虽然一直在听，但听到最后往往只是记住了这几道题的解法，换个方式又不会了.这种重知识方法的归类讲解、轻思维过程的引导，使得学生的学习能力没有得到明显的提升，致使课堂教学效率低下.具体而言，课前学生和老师应该准备什么，课堂做什么，课后又怎样安排，这都是课堂设计中必须深入思考的问题.

2 探究流程

高三复习课，并不是讲授新课，主要目的是让学生发现问题，回顾知识，形成体系.笔者尝试将高三复习课的流程布置如下：前测训练——方法联想——合作研讨——例题讲解——练习反馈.前测训练要求题目全面而又基础，方法联想是梳理知识网络结构，之后是学生合作研讨前测训练中发现的问题，自主完善知识体系，在例题探讨中进一步升华主题，探究本质，最后进行适当训练.

3 教学片段

以下是在陕西省高中数学骨干教师培训课程中开设的一节高三复习课公开课的片段.

就高考中的切线问题而言，已知函数表达式求定点的切线是常考点，这一点学生也不会有太多问题.而面对高考题中的公切线问题，由于学生并未从切线的本质去思考，从而难以顺利解答，因此，本节课的重点在于两条曲线的公切线问题的处理.由于学生对多个参数问题的化归和转化能力有所不足，所以本节课的难点是方程的建立和参数的处理.

3.1 布置前测作业、回顾基础知识

练习1(2017北京)已知函数f(x)=excosx-x，求曲线y=f(x)在点(0,f(0))处的切线方程.

练习2已知函数y=ln(x+1)图象的一条切线方程为y=k(x+1)，则k的值为______.

练习3若函数f(x)=lnx+ax存在与直线2x-y=0平行的切线，则实数a的取值范围是______.

练习4(2016年全国II 16)若直线y=kx+b是曲线y=lnx+2的切线，也是曲线y=ln(x+1)的切线，则b=______.

设计意图通过基础题的考查，让学生了解切线的基本应用的同时，也让他们能够体会切线的本质意义.于此同时，练习3中包含着本节主旨，给学生一定的前期思考.

3.2 深究切线本质、引出课堂主旨

师：昨天作业中的问题主要是什么问题？

生：函数图象的切线问题.

师：这个问题我们曾经学过哪些处理方法？

生：判别式法、导数法.

师：哪种方法解决此类题最为简洁，为什么？

生：导数法，因为判别式法只适合二次曲线，其他函数的图象不存在判别式.

师：那么，解决切线问题的核心是确定哪些量？

生：一点一方向，切点和切点处的导数值.

师：切线是一条直线，要确定直线就是确定点和方向.

3.3 合作研讨错误、直击问题根源

师：请同学们对这练习答案，小组合作探究自己出现的问题，并组内解决问题.

生：学生板演讨论结果，尝试概括提炼概念与方法.

3.4 例题再现重点、师生攻克难点

师：给出思考时间，思考后继续追问需要解决什么问题，和练习四有何异同，范围问题需要建立不等关系，曲线及切线问题有何等量关系和不等关系？

生：切点处有等量关系，函数值相等和斜率值相等.

师：大家都是这样思考的吗，不妨尝试一下.

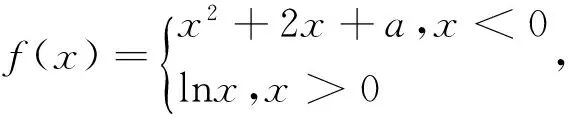
(Ⅲ)若函数f(x)的图象在点A、B处的切线重合，求a的取值范围．

设计意图：通过经典高考题，凸显高考中切线本质考查，同时，提升学生分析问题、转化问题、解决问题的能力.同时，将学生出现的疑问和错误让其他学生现场解答，再次提升能力.

3.5 师生共同提炼、布置练习巩固

提升探究：已知函数f(x)=x2-x+t,t≥0,g(x)=lnx,直线l与两函数都相切，对于确定的正实数t，讨论直线l的条数，并说明理由.

4 几点思考

4.1 发现问题是起点

就教师而言，互联网时代，学生有诸多方式辅助学习，因此教师首先需要知道学生想要什么，进而知道自己需要重点准备什么，最后是通过怎样的方式引导学生，引导的过程要讲究方法；对学生而言，预习发现问题，课堂深入思考、解决认知冲突，课下对课堂知识再巩固，这是教与学的本质所在，所以说问题的设计要有更好的针对性.

4.2 认知冲突是关键

对问题有了准确定位和识别后，就需要联想解决此类问题的常见方法，先想想以前的方法能否解决问题，解决这个问题涉及到几个量、能消去哪个量、有哪些等式或者不等式可以表达问题、最终问题是一个我们熟知的什么问题，怎么解决.

4.3 问题识别是根本

通过对问题的分析，能够识别出问题的本质，对同一问题的不同表达方式能够提出流程化的算法步骤，提高分析问题的能力，养成发现问题——识别问题——解决问题的问题研究方法，长期坚持，定能事半功倍，轻松应考.