疏而不漏有妙招
——关于动点问题中分类讨论的几种技巧
2018-02-26湖北省宜昌市第九中学
湖北省宜昌市第九中学
窦正安 (邮编:443000)
分类讨论思想是数学中重要的思想方法之一,对于增强学生逻辑思维的严密性大有裨益.在若干数学问题中,动点问题因常伴有分类讨论而成为学生们的一大困惑.在分类讨论时如何才能做到不重不漏呢?笔者撷取几例加以剖析,以飨读者.
1 根据几何性质确定动点位置
解题思路运用几何性质确定动点位置的关键是能根据几何性质分析出动点所在的轨迹,画出轨迹便可找出点的位置.

图1
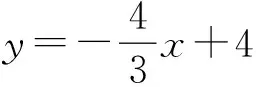
(1)求M、N两点的坐标;
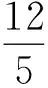
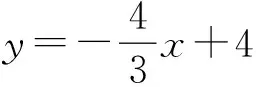
简解(1)M(3,0),N(0,4);

图2

当点P在直线MN的下方时,用上述的方法同理可求得P3(0,0).
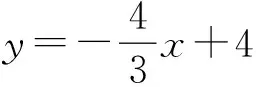
2 画“趋势线”确定动点位置
解题思路画“趋势线”确定动点位置的基本做法就是让动点在其轨迹上动起来,画出对应的趋势线,有几种情况便一目了然了.

图3
例2如图3,已知抛物线y=-x2+bx+c与一直线相交于A(-1,0),C(2,3)两点,与y轴交于点N.其顶点为D.
(1)抛物线及直线AC的函数关系式;
(2)若抛物线的对称轴与直线AC相交于点B,E为直线AC上的任意一点,过点E作EF∥BD交抛物线于点F,以B、D、E、F为顶点的四边形能否为平行四边形?若能,求点E的坐标;若不能,请说明理由.
分析根据题意分析出EF=BD是解决第(2)题的基础,而能否正确写出EF的长度表达式是本题的关键.
简解(1)抛物线的函数解析式为:y=-x2+2x+3,直线AC的函数关系式为:y=x+1;
(2)易求D(1,4)、B(1,2),则BD=2,由题意知:EF=BD=2,设E(n,n+1),则F(n,-n2+2n+3),
当E在F点的上方时,
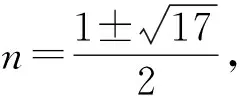

当E在F点的下方时,
EF=(-n2+2n+3)-(n+1)=-n2+n+2=2,
解之得:n1=0,n2=1(舍),此时n+1=1,
故E(0,1);

点评本题的关键是E点和F点的上下位置不确定,如果能画出E点在直线AB上运动时对应的EF的趋势线,便会直观地发现E、F上下位置的不同情况,同时结合EF=2也可以直观地发现一共有3种情况,对于计算的最终结果给予了最直观的印证.
3 运用数形结合 弥补思维缺失
解题思路运用数形结合的思想以数解形,即把几何问题代数化,从而避免分类的不完整,弥补思维上的缺失.
例3同例2
分析在上题中根据题意易知EF=BD=2.如果我们忽视了E、F的上下位置,那么怎样做才能弥补思维的缺失呢?很简单,只要在求EF表达式的时候加上绝对值就不会漏解了.
简解由题意知:EF=BD=2,
设E(n,n+1),则F(n,-n2+2n+3),
则EF=|(n+1)-(-n2+2n+3)|=|n2-n-2|=2,
所以n2-n-2=2或n2-n-2=-2,


点评我国著名数学家华罗庚曾说过:“数缺形时少直观,形少数时难入微”.本题若从代数的角度考虑问题,则无需讨论E、F两点的上下位置,只需在求EF的表达式时加上绝对值,便可回避因忽视两点上下位置而漏解的错误.正可谓:形有数时可入微!
