一类含有“任意性、存在性”问题的求解策略

安徽省太和中学

杨发廷 (邮编：236600)

在高考和模拟试题中经常出现一类函数存在性和任意性问题，它们有时出现在压轴题、把关题位置，是考试的热点之一.这类问题往往又是学生难以理解的知识,很多学生对这些问题模糊不清、模棱两可，而这类知识在学生进入大学后，继续学习高等数学时显得很重要，这类问题弄不清楚，也会影响他们对高等数学的学习,如高等数学的基础问题:数集的确界、极限的“ε-N”定义等,对于这样的衔接性问题,都需要理解好任意性、存在性的问题，才能理解好相关的概念.对于这类问题会涉及函数、不等式、方程等知识，综合性较强，很多学生一直都有“恐函症”，若这类问题再与“任意性、存在性”等逻辑用语相结合,又增“恐逻辑症”,更是难上加难,导致很多同学一见任意、存在就发懵,下面结合实例来辨析和整理含有“任意性、存在性”问题的解题策略.

1 含有不同变量的函数等式关系问题

策略1对于不同函数、不同变量的含有任意、存在的相等关系的问题可转化为相应函数的值域之间的关系，常见情况如下：

(1)∀x1∈D1,∃x2∈D2,f(x1)=g(x2)，可转化为{f(x)|x∈D1}⊆{g(x)|x∈D2}，

(2)∃x1∈D1,∃x2∈D2,f(x1)=g(x2)，可转化为{f(x)|x∈D1}∩{g(x)|x∈D2}≠∅，

(3)∀x1∈D1,∀x2∈D2,f(x1)≠g(x2)，可转化为{f(x)|x∈D1}∩{g(x)|x∈D2}=∅.

例题1已知函数f(x)=x2-2x,g(x)=ax+2(a>0)，若∀x1∈[-1,2],∃x2∈[-1,2]，使得f(x1)=g(x2)，则实数a的取值范围是______.

分析对于两个不同函数f(x)、g(x)，两个不同变量x1、x2，题中条件含有任意、存在的相等关系，把相等关系转化为函数值域之间的关系.

2 含有不同变量的函数不等式关系问题

策略2对于不同函数、不同变量的含有任意、存在的不等关系问题可转化为相应函数的最值之间的关系，常见情况如下：

(1)∀x1∈D1,∃x2∈D2，使f(x1)≥g(x2)，可转化为[f(x)]min≥[g(x)]min；

(2)∀x1∈D1,∀x2∈D2，都有f(x1)≥g(x2)，可转化为[f(x)]min≥[g(x)]max；

(3)∃x1∈D1,∃x2∈D2，使f(x1)≥g(x2)，可转化为[f(x)]max≥[g(x)]min.

分析对于两个不同函数f(x)、g(x)，两个不同变量x1、x2，题中条件含有任意、存在的不等式关系，把不等关系转化为函数最值之间的关系.

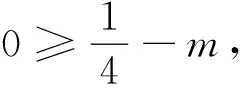
(1)若对任意x1∈[0,2]，任意x2∈[-1,3]，使得f(x1)≥g(x2)成立，求实数m的取值范围.

(2)若对任意x1∈[0,2]，存在x2∈[-1,3]，使得f(x1)=g(x2)成立，求实数m的取值范围.

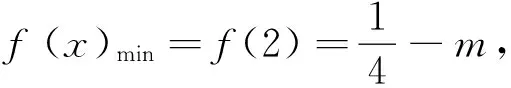
练习：

已知函数f(x)=2k2x+k,x∈[0,1],函数g(x)=3x2-2(k2+k+1)x+5,x∈[-1,0].

若对任意x1∈[0,1]，存在x2∈[-1,0]，使得g(x2)=f(x1)成立，求k的取值范围.

变式1若存在x1∈[0,1],x2∈[-1,0]，使得g(x2)=f(x1)成立，求k的取值范围.

变式2若存在x1∈[0,1]，x2∈[-1,0]，使得g(x2)>f(x1)成立， 求k的取值范围.

变式3若对任意x1∈[0,1]，存在x2∈[-1,0]，使得g(x2)

总之，对函数中的存在性与任意性问题，可把相等关系问题转化为函数值域之间的关系问题，不等关系转化为函数的最值问题.解题中要注意数学思想方法的应用:如转化与化归思想、数形结合思想、分类讨论思想等.

关于任意性、存在性的语言,我们的学生并不感觉陌生,在函数的概念中就涉及到它,同时在函数的单调性与奇偶性中也反复强调“任意”二字的内涵,又在系统的研究特称命题和全称命题的否定中进行了深化.以上各种变式题的解决均是从函数的最值、值域的角度解决考虑的.事实上, 任意性、存在性问题实质就是求函数的最值问题，但要分清是求相关函数的最大值还是最小值问题.说到底仍是从两个集合关系的角度分析问题,当我们的学生能够从集合的观点看待有关任意性、存在性的问题时,他们能“宏观上站得高,微观上看得深”,真正理解好这类问题，相信在遇到类似的问题时不再困惑迷茫.