习题为源生拓展 能力为本蕴发展——基于圆的一个最值问题题根的应用与拓展

江苏无锡市格致中学

陈 锋 (邮编：214125)

江苏无锡市东绛实验学校

薛 莺 (邮编：214125)

1 背景

动点运动的最值问题是近几年中考的热点和难点之一，这类中考试题多如牛毛，如果只是一味地见题做题，不对试题的本质进行研究和归纳整理，进而形成通性通法，则容易形成题海战术，不利于发展学生的数学思维.笔者在研究近几年的中考真题和模拟卷中，发现这类试题形式看似千变万化.但解题的本质是一样的，他们有着相同的本源，即“题根”，本文就是通过探究一个圆的最值问题的求解，来说明这个“题根”的精彩应用与拓展.

2 题根

2.1 问题

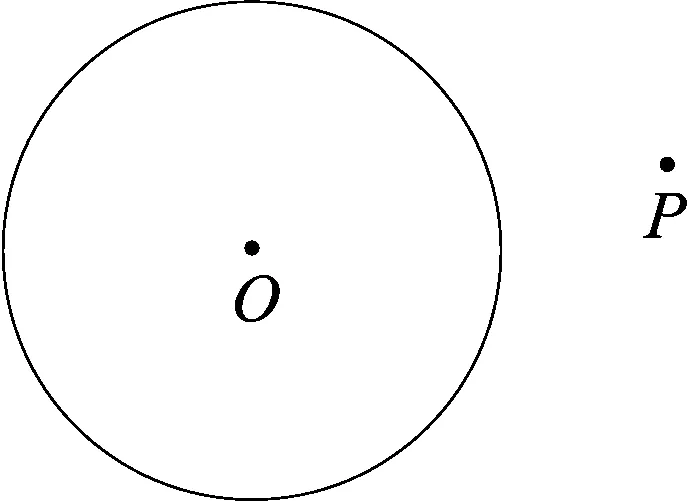
图1

(苏课版九年级上册教科书补充习题)如图1，P是⊙O外的一定点，试探求点P与圆上点的最小距离与最大距离.

2.2 解析

这个问题的本源是两点之间的距离，其中，一个点是圆外的一个定点，另一个点是圆上的动点.从变与不变的哲学辩证关系入手，我们发现，这里有两个定点，分别是点P点O，无论这个动点在圆上如何运动，这两个点的位置始终是不变的，再从特殊与一般的辩证关系出发，我们能自然生成作直线PO，如图2，直线PO与⊙O交于M、N两点，那么M、N两点是否就是我们所需要找的特殊点？我们需要进一步思考.

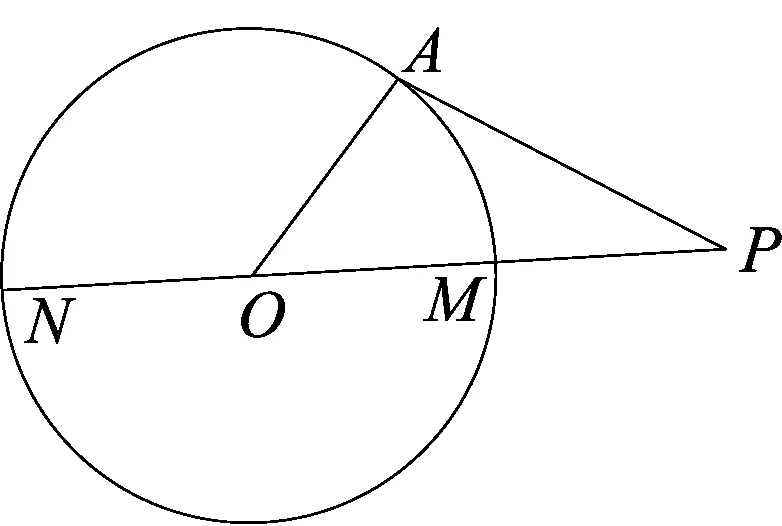
图2

如图2，在⊙O上任取一点A，连接OA、AP，易得：AO+AP≥OP(当O、A、P三点共线时，取等号)，所以AP≥OP-OA，所以AP的最小值=OP—OA=OP—OM=PM，即如果点P与⊙O上的所有点都连接起来，那么，PM的长是所有这些线段长度中的最小值.

因为OP+OA≥AP(当O、A、P三点共线时，取等号)，所以AP的最大值=OP+OA=OP+ON=PN，即如果点P与⊙O上的所有点都连接起来，那么PN的长是所有这些线段长度中的最大值.

综上所述，如图2所示，P是⊙O外的一定点，直线PO与⊙O交于两点M、N，其中PM的长度是点P与圆上各点间的最小距离，PN的长度是点P与圆上各点间的最大距离.

3 演绎

可以发现，求这类线段长的最值问题，要将题根的解法运用进去，这条线段的两个端点，必然一个是定点，另一个在一个定圆上运动，基于对题根的理解，我们明确解题的方向：寻找是否有线段的另外一个端点在圆上运动.

3.1 应用1——图中有圆见动点，利用条件直接运用题根

图3

例1(2014年三明市中考题)如图3，在Rt△ABC中，∠ACB=90°，AC=BC=2，以BC为直径的半圆交AB于点D、P是弧CD上的一个动点，连接AP，则AP的最小值是______.

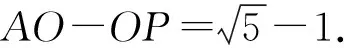
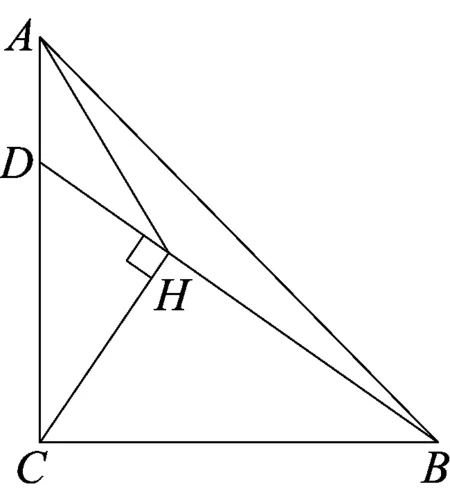
图4

点评对于同类求线段最值的问题，如果线段的两个端点，一个点是圆外的定点，另一个点是圆上的一个动点，那么，我们可以直接运用题根进行分析和解答.

3.2 应用2——图中无圆思构造，创建隐圆间接运用题根

例2(2016年无锡市区中考二模)如图4，等腰直角△ABC中，∠C=90°，AC=BC=4，D为线段AC上一动点，连接BD，过点C作CH⊥BD于H，连接AH，则AH的最小值为( )

图5

解析点A为定点，所以关键在于确定点H的运动轨迹，由CH⊥AD，得∠CHB=90°，可知点H是在以BC为直径的圆上运动.如图5， 以BC为直径作⊙O，由题意可得，点H的运动轨迹是⊙O在△ABC内部的部分.

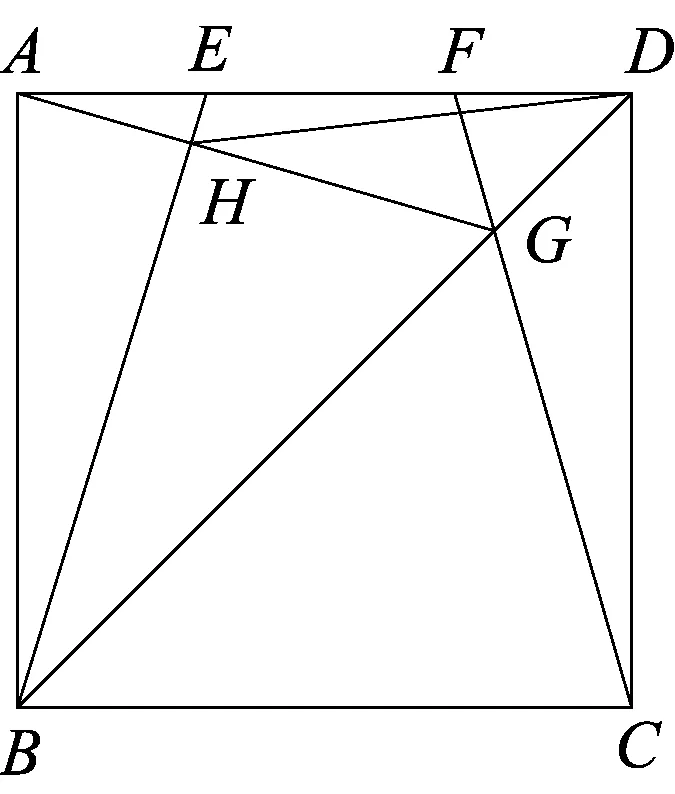
图6

图7

例3(2013年武汉市中考题)如图6，E、F是正方形ABCD的边AD上的两个动点，满足AE=DF，连接CF交BD于点G，连接BE交AG于点H.若正方形的边长为2，则线段DH长度的最小值是__________.

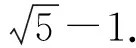
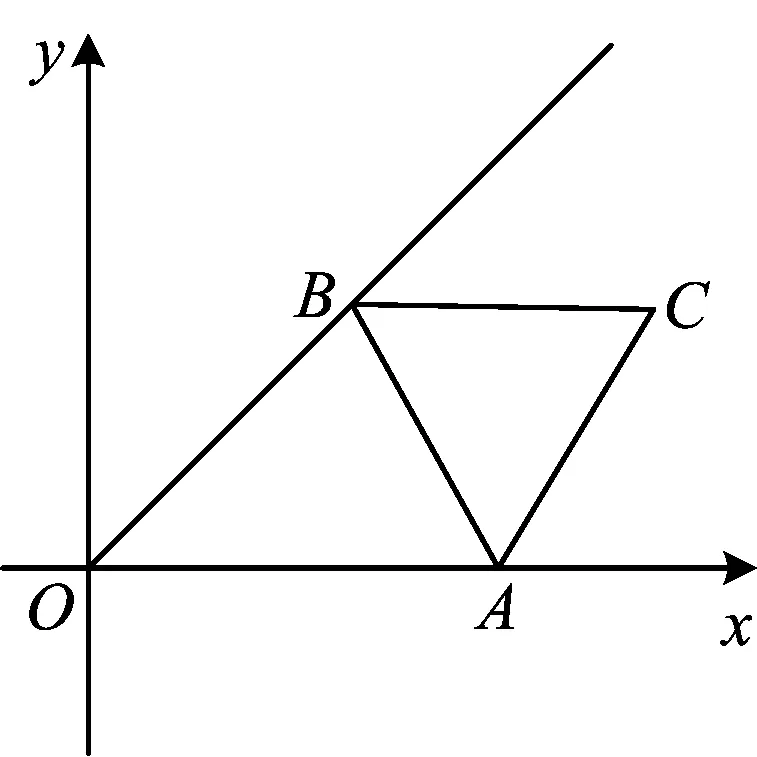
图8

例4(2014年南京市中考模拟题)如图8，在平面直角坐标系xOy中，已知正三角形ABC的边长为2，点A从点O开始沿x轴的正方向移动，点B在∠xOy的平分线上移动，则点C到原点O的最大距离是______.

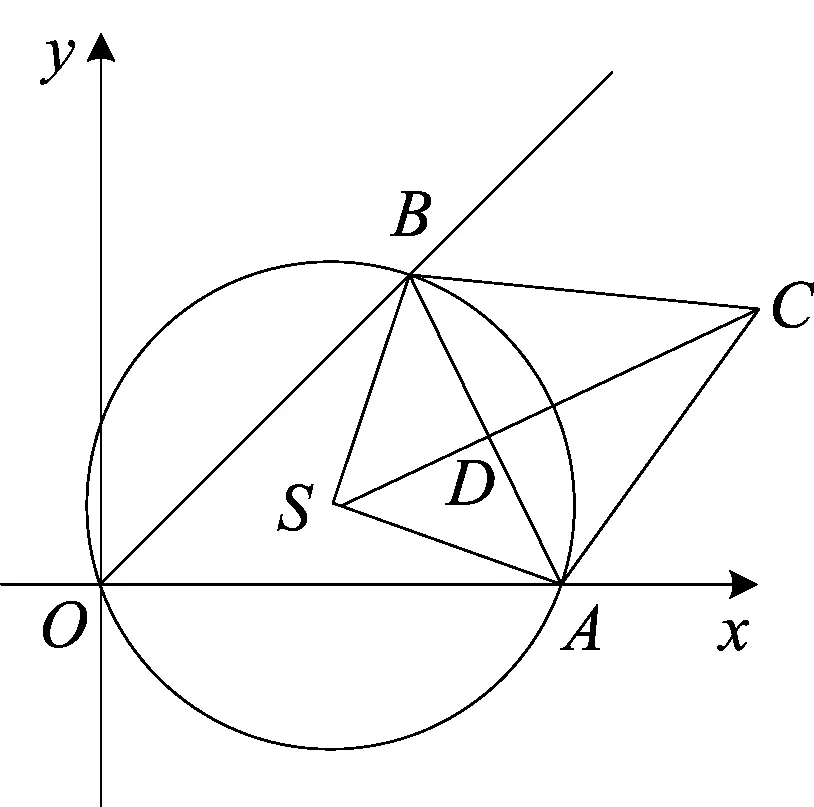
图9

解析运用动静互化的辩证方法，我们可以把△ABC看作是静止的，那么，相对而言，则O点为动点，因为∠AOB=45°，其中点A、B为定点，点O为动点，如图9所示，

由隐形圆的知识，我们可以构造一个⊙S，其中，圆心S与点C在AB的异侧，∠ASB=90°，

图10

点评例题2、 3、4，都还是一定点，一动点的情况.通过挖掘隐含条件，我们可以发现动点其实还是在一个圆上运动，这种在题目和图形中没有直接出现的圆，我们通常把它称为隐形圆或隐圆，挖掘出隐形圆，从而将问题转化为题根进行求解.因为题中并没有直接出现动点在圆上这一条件，所以我们要明晰对“隐圆”的识别：如图10，在△ABC中，定线段AB的长度与∠ACB的大小均为定值，且点C是动点，则点C在△ABC的外接圆⊙O的如图所示的一段弧上运动(点A、B除外).如果没有特别限制，我们要考虑如图10的两种情况.

3.3 应用3——对题根应用的进一步推广

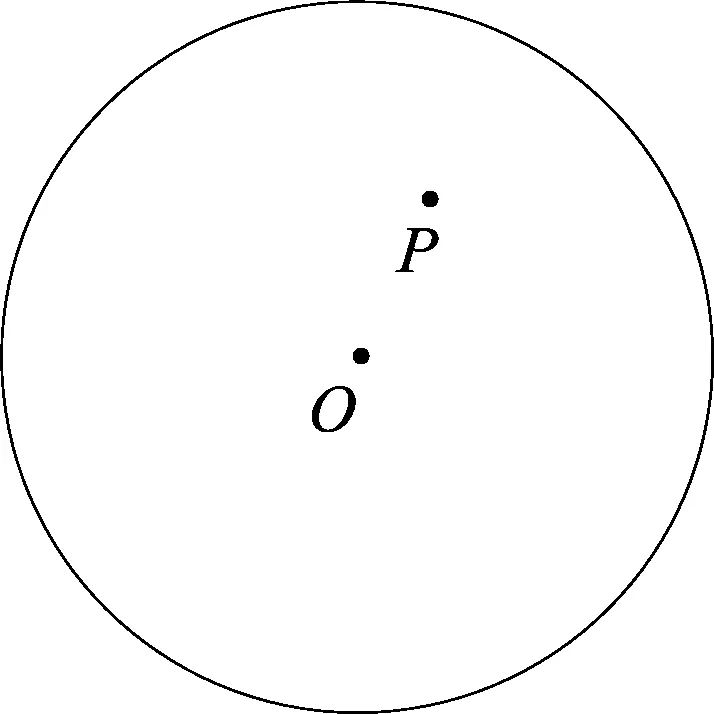
图11

我们不妨进一步思考，是否可以把题根进行推广：如图11，P是⊙O内的一定点，试探求点P与圆上点的最小距离与最大距离.

图12

图13

由对题根的解法我们易得，如图12所示，直线PO与⊙O交于两点A、B，其中，线段PA的长度是点P与⊙O各点距离的最小值，线段PB的长度是点P与⊙O各点距离的最大值.

图14

例5(2015江阴市初三第一学期期末)如图13，已知△ABC的外心为O，BC=10，∠BAC=60°，分别以AB、AC为腰向形外作等腰直角三角形△ABD与△ACE，连接BE、CD交于点P.

(1)判断DC与BE的关系；

(2)求OP的最小值.

图15

图16

图17

例6(2012年浙江义乌中考题)在锐角△ABC中,AB=4，BC=5，∠ACB=45°，将△ABC绕点B按逆时针方向旋转，得到△A1BC1.

(1)如图15，当点C1在线段CA的延长线上时，求∠CC1A1的度数；

(2)如图16，连结AA1、CC1.若△ABA1的面积为4，求△CBC1的面积；

(3)如图17，点E为线段AB中点，点P是线段AC上的动点，在△ABC绕点B按逆时针方向旋转过程中，点P的对应点是点P1，求线段EP1长度的最大值与最小值.

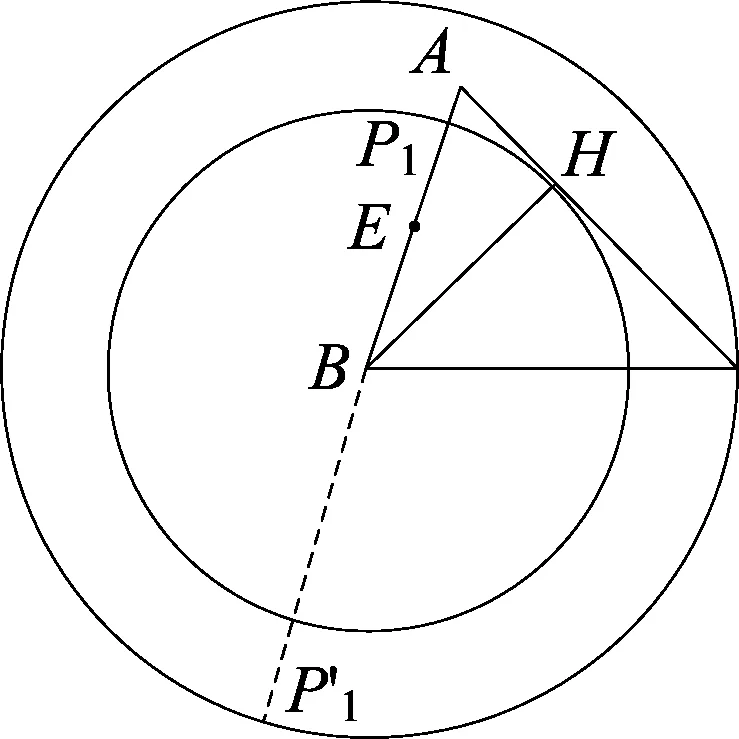
图18

点评我们对题根进行推广之后，题根中的定点，可以是平面内的任何一点，题根适合的范围进行了扩大，解题的主要重点放在动点的确定上，确定动点是否在一个圆上是解题的重点.这个圆可以是已知圆，也可以是隐圆，这对隐圆，我们结合隐圆的判定方式即可.

4 对题根应用的进一步思考

题根在解题时的运用，并不是依样画葫芦的套用，还是要在理解题根的基础上，再对问题展开分析，只有最后适合题根应用的时候，才能进行运用.

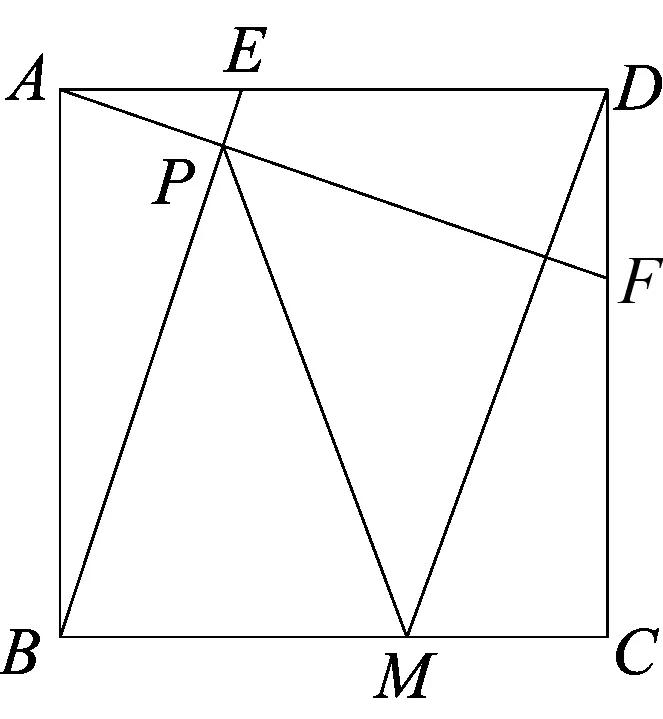
图19

图20

例7(2016年启东市一模)如图19，正方形ABCD中，AB=2，动点E从点A出发向点D运动，同时动点F从点D出发向点C运动，点E、F运动的速度相同，当它们到达各自终点时停止运动，运动过程中线段AF、BE相交于点P，M是线段BC上任意一点，则MD+MP的最小值为__________.

图21

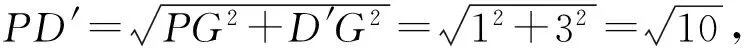
点评思维是灵活的，解题时我们不能局限在一题、一法之中.解一题，得一法，通一片，固然是我们所期待的思维增长的境界，我们其实更希望有更多的“通一片”的产生，从而构造出一个全面的思维观.

5 思考收获

数学新课程标准对原来的初中教学要求进行了重新修订，对原有的教学知识点进行了删减，而进一步强化了对学生能力的要求.使得各地的数学中考试题的设计已经突破了书本知识结论直接运用的简单模式，而是立足教材，对教材例题的典型题根进行不断变化、挖掘和拓展，让试题朝着考查学生的知识转化和能力运用的角度发展，因此对典型题根的研究不仅成为了中考命题的一个热点，也成为教师平时教学的一个方向.这就要求教师以题根这一隐性资源为突破，引导学生进行有效的观察、实验、猜想、归纳、类比等思维活动，不断探寻题根的内涵与外延，力求理顺问题的来龙去脉.这对于激发学生探索精神、求异创新思维等都有积极的意义.同时，这对教师也提出了更高的要求，首先，平时在接触了大量的数学题之后，如果数学教师能对题目中的条件进行分析，做好典型题根的分析和整理，明确题目题根的出处，了解出题者的考查意图，去发现当去除掉题目的背景干扰后隐藏的解决问题的数学本质，因此，加强对题根的学习和运用，对于数学解题，也将是一笔巨大的财富.其次，教学过程中教师注重对典型问题的发生、发散、发展过程的挖掘，明确问题的来龙去脉，寻求问题的解决方法，探究结论推广的可能，是非常重要和必要的.

学习数学离不开解题，解题是掌握数学、学会数学的基本途径，而从手头的第一手资料题根出发，反思题根的解题的思路、解题的方法、解题的过程对培养学生数学的思维显得尤为重要，这样做对于对学生数学思维的培养，也是大有帮助的.只有这样，才能使更多的充满数学味道的鲜活问题为提升学生的数学素养服务.

1 陈锋,薛莺.对初三“圆的复习课”的几点感悟[J] .中学数学(初中版)，2013(5):17-19

2 陈锋,薛莺.多元化的“微探究”：从机械记忆走向理解建构[J].中学数学(初中版)，2013(9):76-78

3 陈锋,薛莺.从课堂“微探究”谈初中数学有效教学[J].中学数学教学参考(初中版)，2013(4)