斜航条件下船舶水动力性能数值仿真
2018-02-26陈志明伍斯杰张娟侯玲黄晓恒
陈志明,伍斯杰,张娟,侯玲,黄晓恒
1广东海洋大学海洋工程学院,广东湛江524088
2太阳鸟游艇股份有限公司,广东珠海519055
3中船黄埔文冲船舶有限公司,广东广州510715
0 引 言
随着船舶建造朝向大型化、高速化的发展以及数字化造船技术的进步,通过计算机仿真模拟来预测新建船舶的水动力性能逐步得到推广应用。目前,通过数值模拟对船舶的快速性能进行预报的技术已颇为成熟,而船舶的水动力性能操纵性却由于问题的复杂性以及人为忽略等因素一直没能得到广泛研究。自1993年国际海事组织(IMO)通过了A.751(18)号决议“船舶操纵性暂行标准”[1]后,2002 年底又通过了 MSC.137(76)号决议“船舶操纵性标准”[2],而近年来由于船舶操纵性较差而频频发生的海难事故,使得人们开始重新重视船舶的操纵性。
国外在船舶操纵性数值研究方面起步较早,积累了较多的经验。早期,Ohmori[3]采用有限体积法对Esso Osaka油轮进行定常斜航运动性能计算,但未考虑自由液面的影响。Alessandrini等[4]采用有限差分方法,采用重叠网格技术和k-ω湍流模型,对Series 60船模做了非定常斜航运动并对相关湍流流场与水动力性能进行了计算,而且考虑了自由液面的影响。Kume等[5]以KVLCCM船舶为研究对象,对该船的水动力力矩及斜航艉伴流场进行试验研究并对试验数据进行了不确定度分析,相关试验结果为数值研究提供了参考依据。Turnock等[6]对KVLCC2模型全附体条件下在浅水中的螺旋桨推力性能进行数值研究,考虑了舵角不同时对螺旋桨推力带来的影响,并将相关结果与试验结果进行了对比,发现数值计算结果在推力和扭矩计算方面有较高的精度。
近些年,我国在船舶操纵性方面也开展了较多的研究并取得了一定的成果。邱磊[7]选取Wigley船型作为研究对象,应用开发的船舶粘性流求解器VSMAN,对漂角较大情况下的斜航运动进行了粘性流场和水动力性能计算。冯松波等[8]通过CFD软件FLUENT计算并分析了KVLCC2模型在不同漂角、不同舵角作用下船—舵系统的横向力与转艏力矩。田喜民等[9]分别采用SSTk-ω与RNGk-ε两种湍流模型对KVLCC2模型进行水动力及艉流场数值分析,并将计算结果与试验值进行了对比,得出SSTk-ω模型更适合斜航粘性水动力计算的结论。
在斜航研究方面,大都只考虑了约束模操纵性试验中的横向力及转艏力矩,而忽略了一定漂角情况下的船体流动分离现象。在国内外学者研究工作的基础上,本文拟使用数值模拟方法对不同漂角下船舶的横向力、船体压力分布进行数值模拟,并将相关结果与试验值进行对比以验证数值结果的有效性,且首次采用数值预报方式对不同漂角条件下的船体流域旋涡结构进行细致的划分,并将船体流动分离现象与船体流线等进行对比分析,可为研究船舶操纵性优劣提供一定的参考依据。
1 数学模型
采用CFD商用计算软件STAR-CCM+对目标船模进行斜航下的数值研究,其基本方法是基于有限体积法求解N-S方程,湍流模型采用SSTk-ω模型,相关控制方程与坐标系如下。
1.1 控制方程
计算域内不可压缩牛顿流体满足连续方程和动量守恒方程[10]:
式中:ui和uj为速度分量的时均值;xi和xj为对应速度分量的2个方向;P为压力的时均值;ρ为流体密度;μ为动力粘性系数;为雷诺应力项;Sj为动量方程的广义源项。
1.2 坐标系
相关坐标系如图1所示。图中:xoy为初始坐标系,满足右手定则;船舶航向U与初始坐标系的x轴方向一致;随船坐标系xooyo与初始坐标系的夹角β为船舶漂角;Fxo与Fyo为船舶所受水动力沿随船坐标系的2个分量;Mz为船舶围绕z轴的转艏力矩。
所有数值计算结果均进行无量纲化处理,相应的横向力系数和转艏力矩系数的无量纲化公式定义均参考文献[11],并将相关数值计算结果与其试验结果进行对比,以验证本文数值计算的准确性。无量纲化公式如下:
式中:Cy为横向力系数;Cm为转艏力矩系数;L为船长;T为船模吃水。
2 计算模型及网格
2.1 几何模型
采用ITTC推荐的KVLCC2标准模型进行数值分析,模型相关参数如表1所示,几何模型如图2所示。
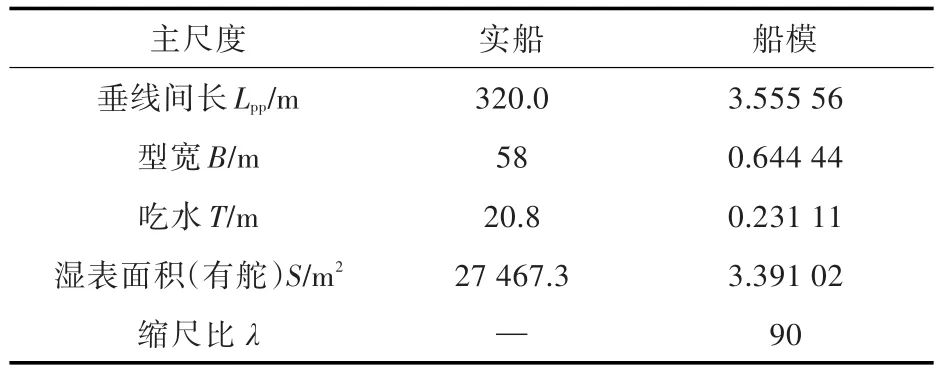
表1 KVLCC2主要参数Table 1 Main parameters of KVLCC2
2.2 网格划分
应用STAR-CCM+自带的前处理功能建立计算域并对其进行网格划分。其中,自由液面采用流体体积(Volume of Fluid,VOF)法捕捉,并在入口、出口和侧壁面进行数值消波,以防止自由表面反射回干扰。计算域及边界如图3所示,其大小为 -1.0Lpp≤x≤4.0Lpp,-1Lpp≤y≤1Lpp和 -1.0Lpp≤z≤2.0Lpp的长方体区域,网格数目为185万。边界层的网格质量通过y+值的范围确定,本次计算的y+值的范围为30~100,说明边界层网格划分合理。
3 计算结果及分析
针对KVLCC2模型(有舵,舵角为0°),分别在漂角较小(β=0°,2°,4°,6°)及漂角较大(β=30°)条件下进行斜航数值计算。船模航速U为对应的设计航速0.84 m/s。对比分析不同漂角情况下船模的水动力性能及流动分离状况,进而为预报对应实船斜航条件下的水动力性能,为实船操纵性能研究提供相关依据。
3.1 粘流下横向力矩及转艏力矩计算分析
分别计算漂角β=0°,2°,4°与 6°时作用在KVLCC2模型上的横向水动力及转艏力矩。并将数值计算结果与试验值进行对比,横向水动力结果如表2及图4所示,转艏力矩结果如表3及图5所示。文中误差定义为数值结果、试验值的差值与试验值的比值。相关试验结果来自文献[11]。
由图4可知,选取SSTk-ω湍流模型,采用RANS方法求解,在漂角较小情况下横向力数值计算结果与试验值相差不大,并且当漂角在0°~6°之间时,漂角越大精度越高。根据图5可知,转艏力矩系数的数值计算结果与试验值吻合度较高,说明数值模拟方法在船舶操纵性计算方面有一定的工程适用性。
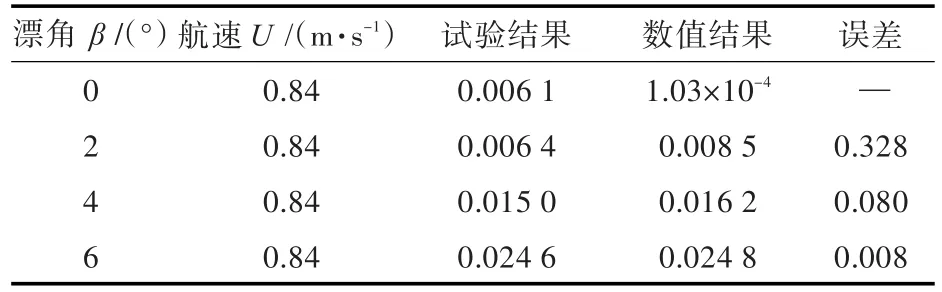
表2 横向力系数Table 2 Lateral force coefficients

表3 转艏力矩系数Table 3 Yaw moment coefficients
3.2 压力分布计算结果
根据数值计算结果绘制船体水动力压力系数CP分布曲线,将漂角β=6°时对应的压力系数曲线与同一母型船舶KVLCC2M的试验值进行对比(试验值来自文献[5]),以验证数值计算结果的准确性。压力系数CP定义如下:
式中,U为船模拖曳速度。
图6所示为KVLCC2模型在漂角β=0°时船体表面水动力压力系数分布的数值结果。图7(a)和图7(c)为KVLCC2模型在漂角β=6°时船体表面压力系数分布的数值结果,图7(b)和图7(d)为KVLCC2M模型在漂角β=6°时船体表面压力系数分布的试验结果。
图7 所示KVLCC2船模与同一母型船舶KVLCC2M的表面压力分布吻合度较高,表明数值方法在小角度斜航压力计算方面有着较高的精度。由图6和图7可知,在漂移角度较小且舵角为0°的情况下,船舵表面压力并没有明显的变化。当漂角β=6°时,船艏的压力中心偏移,压力中心位置在船艏迎流面0.9Lpp处,而船艉的压力中心位置则在0.15Lpp处。由于压力中心的不对称性,会产生转艏力矩,尾部压力中心在背流侧,这与船艉侧涡与舭涡脱离位置基本保持一致。
3.3 船身流动分离
图8 所示为KVLCC2模型在漂角β=0°,6°,30°时的船底涡系结构,其中涡系通过Q-Criterion的方式表示,且Q=10。图9为其对应船体表面约束流线。
由图8可以看出,虽然不同漂角下的船舶涡系结构差异较大,但船底涡核主要由船艏舭涡、船艉侧涡和船艉舭涡3部分构成。当漂角β=0°时,3种主涡的结构形式(船艏舭涡、船艉侧涡、船艉舭涡)可以清楚地辨别并且相对称;当漂角β=6°时,船艏侧涡、船尾发卡涡逐渐被辨别,船艏迎流面舭涡随船体附近向船艉发展,船艉侧涡呈现明显的不对称性;当漂角β=30°时,船艏背流面侧涡、船艉发卡涡可以清楚地观察到,船艏迎流面舭涡与船艏背流面侧涡明显脱离船体向船艉发展,船艏背流面舭涡涡核与迎流面船艉侧涡涡核开始沿船长法向方向发展。从以上现象可知:随着漂角的增大,船艏的流动分离现象相对船艉并不明显,船艏两侧压力不均并非由旋涡脱落造成,而船艉压力的不对称性则主要由船艉侧涡分离造成,这种压力的不均匀会导致横向力与转艏力矩的增加。
由图9可以看出,船体表面约束流线与船体表面涡核分离区域有着较好的一致性。当漂角β=0°时,船体表面约束流线沿船长方向对称;当漂角β=6°时,船底流线基本与来流方向一致,船体背流面一侧流线由于受船艏舭涡与船艏侧涡的影响出现了偏移;当漂角β=30°时,船体表面约束流线分布较复杂,这是由于当漂角较大时,船体周围流动分离,旋涡运动剧烈所造成。
4 结 论
本文主要针对KVLCC2船模在漂角较小(β=0°,2°,4°,6°)及漂角较大(β=30°)的情况下,对其水动力性能及粘性绕流场进行了数值分析,相关数值结果可为船舶操纵性数值研究提供相关依据。主要结论如下:
1)在预报船舶操纵性相关的横向力与转艏力矩方面,采用数值模拟方法满足一定的精度,并且在预报小漂角下的转艏力矩方面精度更高,符合工程应用的要求。
2)当漂角β=6°时,船艏压力中心偏移,压力中心在迎流面0.9Lpp处,艉部压力中心在0.15Lpp处,压力的不对称性与船身绕流场有关。由于压力的不对称性,产生了船舶横向力与转艏力矩。
3)船底涡核主要由船艏舭涡、船艉侧涡及船艉舭涡3部分构成。当漂角较大时,船艏侧涡与船艉发卡涡可以清楚地被观察到。船底涡系分离区域与船身约束流线分离区域相互对应,船身约束流线对于研究斜航条件下的船身旋涡分离脱落具有一定的参考意义。
4)船艏压力不均受流动分离影响较小,船艉压力不均主要是由船艉的侧涡脱离造成,侧涡的脱离导致船舶横向力与转艏力矩增加。
[1]IMO.Interim standards for ship maneuverability[S].International Maritime Organization,1993.
[2]IMO.Standards for ship maneuverability[S].International Maritime Organization,2002.
[3]OHMORI T.Finite-volume simulation on flows about a ship in maneuvering motion[J].Journal of Marine Science&Technology,1998,3(2):82-93.
[4]ALESSANDRINI B,DELHOMMEAU G.Viscous free surface flow past a ship in drift and in rotating motion[C]//Proceedings of 22th Symposium on Naval Hydrodynamics.Washington,DC,USA:[s.n.],1998:491-507.
[5]KUME K,HASEGAWA J,TSUKADA Y,et al.Measurements of hydrodynamic forces,surface pressure and wake for obliquely towed KVLCC2M model and uncertainty analysis[C]//Proceedings of CFD Workshop,Tokyo,Japan:[s.n.],2005.
[6]TURNOCK S R,PHILLIPS A B,FURLONG M.Urans simulations of static drift and dynamic manoeuvres of the KVLCC2 tanker[C]//Proceedings of SIMMAN 2008:Workshop on Verification and Validation of Ship Manoeuvring Simulation Methods.Lyngby,Denmark:[s.n.],2008.
[7]邱磊.船舶操纵相关粘性流及水动力计算[D].武汉:武汉理工大学,2003.QIU L.Computation of ship manoeuvring related viscous flow and hydrodynamic forces[D].Wuhan:Wuhan University of Technology,2003(in Chinese).
[8]冯松波,邹早建,邹璐.KVLCC2船-舵系统斜航水动力数值计算[J].上海交通大学学报,2015,49(4):470-474.FENG S B,ZOU Z J,ZOU L.Numerical calculation of hydrodynamic forces on a KVLCC2 hull-rudder system in oblique motion[J].Journal of Shanghai Jiaotong University,2015,49(4):470-474(in Chinese).
[9]田喜民,邹早建,王化明.KVLCC2船模斜航运动粘性流场及水动力数值计算[J].船舶力学,2010,14(8):834-840.TIAN X M,ZOU Z J,WANG H M.Computation of the viscous flow and hydrodynamic forces on a KVLCC2 model in oblique motion[J].Journal of Ship Mechanics,2010,14(8):834-840(in Chinese).
[10]WILCOX D C.Turbulence modeling for CFD[M].LA California:DCW Industries,Inc.,1994:15-20.
[11]王化明.限制水域操纵运动船舶粘性流场及水动力数值研究[D].上海:上海交通大学,2009.WANG H M.Numerical study on the viscous flow and hydrodynamic forces on a manoeuvring ship in restricted waters[D].Shanghai:Shanghai Jiao Tong University,2009(in Chinese).
