基于局部线性化方法的瘫船稳性敏感性分析及衡准完善

王廷昊 ，顾解忡 ，马骋远 ，马宁

1上海交通大学海洋工程国家重点实验室，上海200240

2高新船舶与深海开发装备协同创新中心，上海200240

3上海交通大学船舶海洋与建筑工程学院，上海200240

0 引言

国际海事组织（IMO）第2代完整稳性衡准考察的5种稳性失效模式包括参数横摇、纯稳性丧失、骑浪/横甩、瘫船稳性和过度加速度。基于诱发各稳性失效模式的必要条件，IMO将衡准划分为第1层、第2层和直接计算衡准（DSA），3个层次的计算复杂度和预报精度逐级提高［1］。瘫船稳性是稳性衡准中考察的第1个基于剧烈横风横摇物理条件的稳性失效模式，也称“气象衡准”。该模式考察的物理情景为：假设船舶失去动力无法推进或操舵并转向至横浪状态，船在风浪联合作用下发生自由漂移和共振横摇运动甚至是最终倾覆［2］。在IMO的瘫船稳性薄弱性衡准方法中，第1层主要基于2008完整稳性规范（2008 IS Code）中“气象衡准”，第2层衡准方法采用的是意大利提出的局部线性化方法。目前，这两层衡准方法基本达成一致，但第2层衡准的标准值仍未确定，第2层衡准和直接计算衡准的定稿工作预计将于2019年完成［3］。

国内外学者针对横浪状态下的船舶大幅横摇运动问题进行过许多研究，主要包括线性化理论和线性化处理方法、非线性动力学的应用以及直接数值模拟方法［4］。在IMO的提案中，针对第2层衡准方法，日本［5］和意大利［6］分别基于分段线性化和局部线性化两类线性化处理方法，提出了较为完善的衡准评估方案。在第55届载重线和渔船安全分委会（SLF）会议上，日本对两类线性化处理方法进行了对比研究，提议将局部线性化方法作为瘫船稳性第2层的衡准方法，分段线性化方法作为某些极端海况下的备选方案［7］。

Vassilopoulos［8］于 1971 年首次提出了局部线性化概念，通过谱分析得到了非线性项的等效统计值。Bulian等［9］基于局部线性化思想，对船舶回复力矩进行局部线性化处理，利用相当面积法计算了船舶在瘫船状态下的大倾角横摇倾覆概率。

本文拟针对瘫船稳性第2层衡准，选取C11集装箱船、某10 000 TEU集装箱船和IMO稳性工作组提供的研究船型CEHIPAR 2792集装箱船，采用局部线性化方法得到横摇运动的等效统计值，并据此计算倾覆概率。在样船计算的基础上，重点探讨船舶各设计参数、波浪谱选取、有效波倾系数以及尺缩系数（Size reduction factor）估计方法等敏感性因素对倾覆概率的影响，并对第2层衡准的标准值选取提出建议。

1 瘫船稳性局部线性化数学模型

1.1 单自由度横摇运动方程

局部线性化数学模型考察船舶的单自由度横摇运动，运动方程无因次化后表示为

式中：φ为横摇角；为无因次阻尼项，其中为无因次处理前的阻尼项，Jxx和ΔJxx为横摇惯性矩及附加惯性矩；为横摇固有频率，其中W为船舶重量，GM为初稳性高；为无因次回复力，其中GZ(φ)为回复力臂；为无因次风倾力矩，是阵风δMwind,tot()t和定常风作用之和；为无因次波浪激励力矩。

波浪激励力矩可由波浪谱进行有效波倾系数修正后计算得到。波浪谱采用Pierson-Moskowitz类型的 Bretschneider双参数谱［10］：

式中：HS为不规则波的有义波高，m；TZ为波浪谱的跨零周期，s；ω为角频率。考察长周期波浪作用特征时，HS和TZ可由北大西洋波浪分布表［10］统计资料的波浪散点图给出；考察短周期波浪作用特征时，回归分析表明两者与定常风速Vw有如下对应关系［4］：

式中，Δ为船舶排水量。风倾力矩可以分为定常风成分Mˉwind,tot和阵风成分 δMwind,tot()t，即

式中：ρair=1.222kg/m3，为空气密度；Cm为风倾力矩系数；v(t)为阵风风速；AL为船舶横向受风面积；Hw和Hyd分别为从风作用中心和波浪作用中心到水线面的距离。

阵风谱函数采用 Davenport谱［10］，表示为

1.2 横摇运动方程局部线性化

局部线性化方法的思路是假设船舶在定常风作用下产生平均横倾角φs，并始终围绕该横倾角做横摇运动。相对平均横倾角φs的横摇运动，可用下面的等效线性方程描述：

式中：x=φ-φs，为相对横摇角；阻尼项采用随机等效线性方法近似得到，

式中：μ，β和δ为一、二和三次项的阻尼系数；σx˙表示横摇角速度的标准差，可以通过迭代计算横摇运动谱的二阶谱矩得到

复原力矩项系数ω0,e在平均横倾角φs附近做局部线性化处理，可得

1.3 横摇运动方程近似解

经局部线性化处理的横摇运动方程为二阶常系数线性微分方程，包含了船舶受到的激励作用和横摇运动响应。将横摇力矩谱代入即可近似得到船舶横摇运动谱：

式中：H(ω)为随波浪频率变化的传递函数；Sm(ω)为无因次的波浪力矩谱。

2 倾覆概率计算模型

2.1 倾覆条件

局部线性化方法求解船舶的等效倾覆角采用相当面积法［2］，即等效线性化处理后的回复力臂曲线、定常风力臂在临界倾覆角范围内所围面积和原回复力臂曲线、定常风力臂在实际倾覆角范围内所围面积相等。求解过程如图1所示。

定义实际倾覆角分别为：

式中：φcap,+和φcap,-分别为顺风向和迎风向的实际倾覆角；φVW+和φVW-分别为顺风向和迎风向的稳性消失角；φcritical为临界角，取进水角φfl和50°的较小值。

则临界倾覆角可按下式计算：

式中：φcap,EA+和φcap,EA-分别为顺风向和迎风向的临界倾覆角；为除去定常风倾力臂的剩余回复力臂曲线；ζ为横摇角取值范围。

2.2 倾覆概率计算

在一定暴露时间内，横摇幅值超过临界倾覆角即认为发生了倾覆。假设船舶的倾覆事件符合泊松分布，可得到给定暴露时间Texp内的倾覆概率为

式中：CS为倾覆概率；取暴露时间Texp=1 h；σCS为横摇角的标准差；TZ,CS为横摇角的跨零周期。计算如下：

在实际船舶运营条件下，需要根据不同海区的波浪统计资料计算每个海况条件下的短期倾覆概率，根据各类海况发生的统计概率进行加权平均后得到特定海区的船舶长期倾覆概率数值，计算公式如下：

3 模型验证与敏感性因素分析

根据前文提到的衡准方法，编制相应的计算程序。首先，以C11集装箱船（APL China号）为例进行衡准计算，并与 SDC4/5/1/Add.3结果［10］进行对比，验证衡准计算模型的可靠性；然后，以某10 000 TEU集装箱船和CEHIPAR 2792船为对象，分析瘫船稳性敏感性与船舶各设计参数的关系。

3.1 样船模型

C11集装箱船、某10 000 TEU集装箱船和CEHIPAR 2792船的基本参数如表1所示。

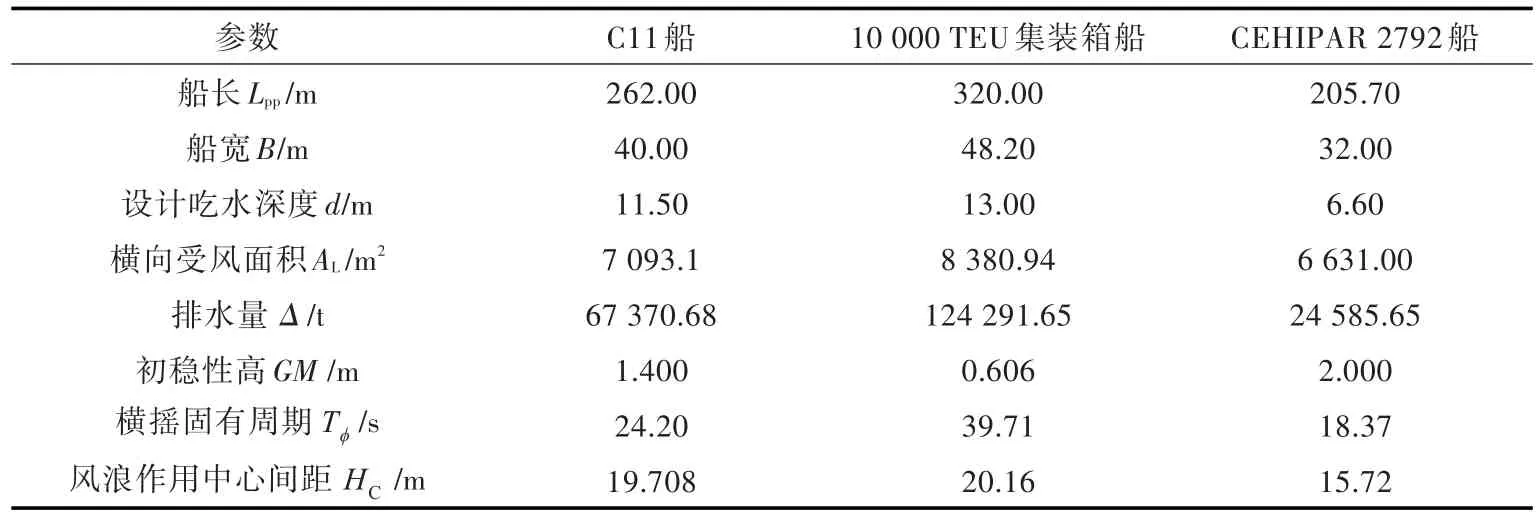
表1 样船基本参数Table 1 Basic parameters of sample ships

3.2 模型验证结果

针对C11船设计吃水载况，利用自编程序计算北大西洋海区波浪散布表所描述海况下的倾覆概率，暴露时间取1 h，程序计算结果和草案算例结果如图2所示。图中，W×CS为对应波浪条件下的船舶倾覆概率。

由图2可见，自编程序计算的结果同草案算例结果保持在同一数量级，且对于全部北大西洋海区波浪散布表描述的海况，计算得到的倾覆概率分布类似，证明了衡准计算模型的可靠性，两者之间的差异可能来自于回复力臂曲线等试验数据差异及曲线拟合精度不同等人为因素。

3.3 倾覆概率敏感性因素分析

3.3.1 船舶设计参数

针对某10 000 TEU集装箱船实际运营中的89个典型装载工况，首先基于局部线性化方法计算了暴露时间Texp=1h的长期倾覆概率。倾覆概率计算结果同各工况下船舶设计参数的对比如图3所示。由于第2层衡准的标准值尚未确定，这里暂时取为0.001［11］。为探究衡准值选取对两层衡准结果一致性的影响，同时进行了第1层衡准计算，并用定常风力矩与回复力矩曲线在迎风横摇角和下向进水角处围成面积之比b/a来表征船舶稳性特征，相关计算方法参见文献［2］，其结果如图4所示。

就本例而言，选择的89例船舶典型装载工况中包含压载（空船、靠港）、设计吃水和满载工况，根据集装箱布置的不同，船舶方形系数Cb略有差异，具体表现为：吃水深度d=4～15.5 m，对应的初稳性高GM=0.7～17 m；方形系数Cb=0.48～0.64。由图3和图4可以看出，随着吃水深度的增加，第2层衡准的倾覆概率结果出现整体先降低后升高的趋势；第1层衡准的面积比b/a则为整体先升高后降低，其含义为船舶稳性特征先改善后恶化，这说明两层衡准结果的趋势保持一致。其中，压载（空船、靠港）工况（吃水深度d=4～8 m）区域倾覆概率结果较高，未通过第2层衡准；设计吃水工况（吃水深度d=11～13 m）区域整体倾覆概率最低；满载工况（吃水深度d=15～15.5 m）区域整体倾覆概率略有提高，但依然可以通过衡准要求。而方形系数对倾覆概率的影响似乎并不明显。为进一步探索船舶吃水深度对倾覆概率的影响，分别考虑了联合风浪作用、单独风作用、单独浪作用下，在不同吃水深度下暴露时间Texp=1h时船舶倾覆概率，结果如图5所示。

由图5可见，当单独考察波浪作用时，船舶吃水深度增大引起倾覆的概率整体逐渐降低，这是由于船舶吃水深度增大引起船舶初稳性高GM降低，横摇固有周期Tφ增大，并逐渐偏离波浪谱峰周期，导致船舶横摇运动响应减小；当单独考察风的作用时，只有在吃水深度较大区域的倾覆概率出现增高，这是因为在满载条件下，船舶初稳性高GM较小，船舶横摇运动周期较大，受到低频阵风的作用更为明显。因此，在船舶各装载工况中，随着船舶吃水深度的增大，倾覆概率先减小后增大；其中压载时波浪对瘫船倾覆概率的影响大，而满载时风的影响大。

此外，对本例中出现的船舶压载（空船、靠港）工况两层衡准一致性矛盾的情况进行了分析。此工况下船舶初稳性高GM较大，稳性消失角φVW已经高于临界角50°和进水角φfl，此时较高的初稳性高GM非但不会使实际倾覆角φcap增大，反而会使临界倾覆角φcap,EA降低，因此计算得到的倾覆概率偏高。考虑到衡准的一致性，如果将第2层衡准的标准值取为0.02，则衡准通过率可由85.3%提升至96.6%，且此时除空船（Light weight）或靠港（Docking）状态外全部可通过衡准。

3.3.2 波浪谱

图6给出了在定常风速均为Vw=20 m/s时4种常用的波浪谱函数图像。图7给出了4种波浪谱下得到的CEHIPAR 2792船倾覆概率曲线。

由图6和图7可知，对于我国沿海波能谱、PM谱和ITTC双参数谱，三者波浪谱函数图像形态相近，ITTC双参数谱谱峰位置相对靠近高频区域，偏离船舶横摇固有频率，相同定常风速下倾覆概率计算结果相对较小；我国沿海波能谱谱峰幅值和波浪激励力矩最大，因此倾覆概率计算结果也最大；JONSWAP谱虽然谱峰值高于PM谱和ITTC双参数谱，但谱峰处波浪频率范围很窄，波能较低，倾覆概率计算结果也最小。可见，我国沿海波能谱的倾覆概率计算结果高出其他3种谱较多，JONSWAP谱和ITTC双参数谱的倾覆概率计算结果相对接近，对船舶抵抗倾覆能力的评估较为乐观，SDC4草案中选取的PM谱结果介于中间，衡准安全裕度适中。

3.3.3 有效波倾系数

以CEHIPAR 2792为研究船型，讨论有效波倾计算方法对衡准结果的影响。有效波倾的计算方法有3种：1）基于等效剖面的简化方法（SIM法）的计算结果［10］；2）SDC1衡准草案中基于STF切片法的直接计算结果［2］；3）我国海船稳性规范中的经验公式（EMP法）［13］。在SDC4衡准草案中，提出以SIM法作为第2层衡准中有效波倾系数的标准取法。图8和图9分别为CEHIPAR 2792船在正常吃水深度下采用3类有效波倾系数计算方法得到的有效波倾系数和横摇波浪力矩谱。

由图8可见，采用3种方法得到的有效波倾系数图像形态略有不同，SIM法和STF法有效波倾系数在低频区域随波浪频率振荡，当频率增至高频区域后，趋近于零，EMP法则取有效波倾系数为恒定值。这导致得到的横摇波浪力矩谱形态存在差异（图9），3种方法得到的第1个谱峰位置都接近0.5，EMP法由于有效波倾系数整体偏高，故峰值相对较高，SIM法居中，STF法最低。

图10给出了CEHIPAR 2792船采用3种有效波倾系数计算方法得到的倾覆概率曲线。可以发现，在15～30 m/s风速范围内，EMP法得到的倾覆概率值整体偏高，STF法最小，SIM法居中，这与波浪力矩计算结果趋势一致。因此可以认为，SDC4衡准草案中提出的有效波倾系数取法是一种衡准安全裕度较为适中的方案。

3.3.4 尺缩系数

以CEHIPAR 2792为对象，讨论尺缩系数对衡准结果的影响。选取两类尺缩系数计算方法：

1）SDC4草案中取恒定值的方法（CON法）［10］；

2）Vickery［13］基于风洞试验给出的经验公式（EMP法）。其中EMP法在SDC1草案中作为尺缩系数计算方法的可选项给出。图11和图12给出了以上2类方法得到的尺缩系数结果及CEHIPAR 2792船的阵风力矩谱。

由图11和图12可见，EMP法得到的尺缩系数随阵风频率的增加逐渐减小，在高频区域趋近于零，而SDC4草案中推荐的CON法结果整体高于EMP法，受此影响，CON法得到的阵风力矩谱峰值略高，对应的频率略大。图13进一步给出了采用两类尺缩效应计算方法得到的倾覆概率曲线。从中可以发现，CON法相较于EMP法，最终倾覆概率在风速20～25 m/s范围内略高，但差异并不显著，可以认为采用CON法对尺缩系数进行估算的精度满足要求。

4 结 论

基于IMO最新制定的瘫船稳性第2层衡准规则要求，采用局部线性化方法对船舶在横风横浪中的大幅横摇运动进行近似简化研究，并据此得到倾覆概率计算结果。

1）局部线性化法通过谱分析得到横摇运动方程中非线性项的等效统计值，并基于相当面积法有效求解船舶在横风横浪下的倾覆概率，计算结果显示：随着船舶吃水深度的增大，倾覆概率先减小后增大；其中压载时受波浪作用明显，而满载时风的影响大。

2）实船校核时，对于某些GM值较高船舶的压载工况，应用局部线性化方法可能出现衡准结果与第1层结论不一致的情况，建议将第2层衡准的标准值提升至0.02。

3）不同的波浪谱及有效波倾系数近似取法对倾覆概率计算的影响是存在的，应当根据海区特征选取适当的波浪谱，目前SDC4草案中的取法可以作为一种安全裕度适中的方案。

4）在本文算例中，不同尺缩系数取法对倾覆概率计算的影响较为有限，采用SDC4草案中取恒定值的方案精度满足要求。

［1］IMO.SLF 54-WP.3.Report of the working group（part 1）（working group）［R］.London：IMO，2012.

［2］IMO.SDC 1/INF.6.Vulnerability assessment for deadship stability failure mode［R］.Italy：IMO，2014.

［3］IMO.SDC 4/INF.8.Finalization of second generation intact stability criteria：direct stability assessment-information for further discussion［R］.Germany：IMO，2016.

［4］曾柯.船舶瘫船稳性衡准技术研究［D］.无锡：中国舰船研究院，2015.ZENG K.A study on criteria of dead ship stability［D］.Wuxi：China Ship Research and Development Academy，2015（in Chinese）.

［5］IMO.SLF 52/INF.2，ANNEX 2.Draft vulnerability criteria and their sample calculation［R］.Japan：IMO，2009.

［6］IMO.SLF 52/INF.2，ANNEX 3.Higher level dynamic stability assessment for dead-ship condition［R］.Italy：IMO，2009.

［7］IMO.SLF 55/3/11.Comparison study of draft level 2 vulnerability criteria for stability under dead ship condition［R］.Japan：IMO，2013.

［8］VASSILOPOULOS L.Ship rolling at zero speed in random beam seas with nonlinear damping and restoration［J］.Journal of Ship Research，1971，15（4）：289-294.

［9］BULIAN G，FRANCESCUTTO A.A simplified modular approach for the prediction of the roll motion due to the combined action of wind and waves［J］.Proceedings of the Institution of Mechanical Engineers，Part M：Journal of Engineering for the Maritime Environment，2004，218（3）：189-212.

［10］IMO.SDC4/5/1/Add.3-ANNEX 4.Draft explanatory notes on the vulnerability of ships to the dead ship stability failure mode［R］.Japan：IMO，2016.

［11］IMO.SLF 53/INF.10，ANNEX 7.Draft direct assessment on stability under dead ship condition and its numerical validation［R］.Japan：IMO，2010.

［12］盛振邦，刘应中.船舶原理（下）［M］.上海：上海交通大学出版社，2004：360-363.

［13］VICKERY B J.Load fluctuations in turbulent flow［J］.Journal of the Engineering Mechanics Division，1986，94（1）：31-46.