智能汽车非时间参考的螺旋弯曲坡道路径跟踪控制
2018-02-21江浩斌张旭培马世典
江浩斌,张旭培,马世典
(江苏大学 a.汽车与交通工程学院; b.汽车工程研究院, 江苏 镇江 212013)
自动泊车、自动驾驶等智能化技术是目前国内外汽车技术的研究热点[1-2]。全工况自主泊车既是自动泊车技术的发展方向,也是无人驾驶汽车的关键技术之一。对于智能汽车而言,在从地面进入地下停车场过程中,经常遇到螺旋弯曲坡道,要完成从地面到地下停车场的自主泊车,关键技术之一是智能汽车能够在螺旋弯曲坡道上安全稳定地自主行驶,其中在螺旋弯曲坡道上的路径跟踪尤为重要。
二维(平面)路径跟踪控制已有不少研究成果,大多采用减少预瞄横向偏差的控制策略进行路径跟踪控制[3-10],但是预瞄横向偏差在螺旋弯曲坡道上较难定义并获取。智能汽车在空间约束较强的螺旋弯曲坡道上自主行驶时,可能存在长时间停车避撞的行为,且基于时间变量的路径跟踪控制策略受时间和车速的影响较大,当智能汽车行驶过程中移动停止时,控制误差会随时间延长不断增大[11]。因此,当采用非时间参考控制策略进行路径跟踪时,控制器输出是基于设定的非时间参考量,当智能汽车停车避撞或停止移动,非时间参考量停止增加,控制器输出停止变化,相应控制误差不再增加[12-13]。目前,针对智能汽车在进入地下停车场的螺旋弯曲坡道中自主行驶路径跟踪的相关研究尚未见公开报道。
本文针对智能汽车在螺旋弯曲坡道内自主行驶的路径跟踪问题,通过分析汽车在螺旋弯曲坡道行驶的特点,建立智能汽车三维运动学模型;针对在三维空间内位置跟踪的三参数特点,提出以Z轴位置变量为非时间参考的因变量的路径跟踪控制方法,将三维空间位置跟踪的3个参数转化为二维平面位置跟踪的2个参数,期望路径就是一条几何曲线[14];采用非时间参考控制策略进行螺旋弯曲坡道路径跟踪,通过Carmaker与Simulink联合仿真,验证非时间参考控制律在螺旋弯曲坡道的路径跟踪的有效性。
1 智能汽车在弯曲坡道的自主行驶过程分析
智能汽车在地下停车场弯曲坡道的自主行驶过程如图1所示,具体描述如下:
1) 地下停车场弯曲坡道自主行驶系统开启后,通过车身四周的雷达传感器检测汽车相对于坡道的位置。
2) 自主行驶系统根据弯曲坡道高精地图及汽车当前位置,确定自主行驶的起始点并规划行驶路径。
3) 自主行驶系统根据规划的路径,通过控制车速和方向盘转角使汽车沿目标路径行驶。
4) 在路径跟踪的过程中,自主行驶系统需要通过传感器实时监测前方行驶区域是否有障碍物,若前方行驶区域存在障碍物,自主行驶系统需在狭小空间内进行车辆避障控制。
5) 当智能汽车自主行驶到地下停车场弯曲坡道的出口(即地下停车场弯曲坡道),自主行驶过程结束。
假设智能汽车在地下停车场弯曲坡道的行驶路径已成功规划,本文将进行步骤3)的工作,即对自主行驶中的汽车路径跟踪控制进行研究。

图1 智能汽车弯曲坡道自主行驶决策流程
2 车辆运动学模型
智能汽车在进入地下停车场的弯曲坡道自主行驶速度较低,因此忽略汽车的侧向滑动,将汽车视为具有非完整性的运动系统,其运动学方程可表示为:
(1)

由Ackerman转向几何原理可知:R=L/tan(φ),其中:φ为前轴等效转角;L为车辆轴距。车辆在X-Y平面的转向运动几何原理如图2所示。

图2 Ackerman转向运动几何原理
3 非时间参考路径跟踪控制律
3.1 路径跟踪问题分析
智能汽车在地下停车场弯曲坡道自主行驶的路径跟踪问题可描述为:汽车在弯曲坡道内低速自主行驶,自主行驶系统采用合适的方向盘转角控制律调整方向盘转角,使智能汽车沿规划好的路径自主行驶。由式(1)可知,当智能汽车轴距及当前坡道坡度确定后,汽车行驶速度及方向盘转角决定了后轴中点的行驶轨迹。因此,选择后轴中点为研究对象,在低速行驶工况下,研究智能汽车方向盘转角控制策略,控制汽车后轴中心沿已规划的路径行驶。
3.2 非时间参考路径跟踪控制律
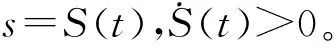
(2)
对于任意给定的空间几何路径f(xr,yr,zr,θr)=0,选取一个随时间单调递增的非时间参考量s,根据非时间参考量s寻找反馈控制律,对于任意给定ε>0,存在S>0,使得当s>S时,|f(x,y,z,θ)-f(xr,yr,zr,θr)|<ε,f(xr,yr,zr,θr)为目标路径,xr、yr、zr、θr为轨迹上的目标位置[15]。其中:xr为智能汽车后轴中心的目标X轴坐标,yr为智能汽车后轴中心的目标Y轴坐标;θr为车辆后轴中心的X轴坐标映射到目标路径上的航向角。由于本文选择-z(t)为非时间参考量,因此仅需考虑X-Y平面位置误差和航向角误差。根据图3所示的X-Y平面跟踪偏差,确定路径跟踪偏差,如式(3)所示。

图3 路径跟踪偏差
路径跟踪偏差方程为:
(3)
其中:ye为车辆在Y轴方向上的位置距离偏差;θe为航向角偏差。
由非时间参考量s=-z(t),非时间参考的路径跟踪偏差状态方程为:
(4)
即:
(5)
式中ρr为目标路径的曲率。
令:
其状态方程为:
(6)
令φ控制律为:
(7)
其中常数k1>0,k2>0,k1、k2分别为智能汽车位置偏差反馈系数、航向角偏差反馈系数,得:
(8)

4 路径跟踪仿真及结果分析
4.1 联合仿真模型搭建
本文运用Simulink与Carmaker进行联合仿真实验。Carmaker是一款成熟的参数化、面向总成特性的车辆动力学仿真软件。相对于Carsim等仿真软件,Carmaker具有以下几个特点:① 整车模型模块化更突出,更易进行模块更替;② 道路模型搭建容易,具有多样性;③ 拥有高精度的传感器,环境参数可以被传感器获取并输出;④ 可建立精确的动力学模型。
在Carmaker中建立道路模型和车辆模型,在Simulink中建立路径跟踪控制器模型,如图4所示。车辆参数按照实际车辆参数设置,如表1所示。

图4 Carmaker与Simulink联合仿真

参数数值轴距L/m2.6最大方向盘转角ϕmax/(°)540最大方向盘转速Ωmax/[(°)·s-1)]450转向系角传动比K19最大前轴等效转角φmax/(°)30
地下停车场弯曲坡道一般根据螺旋线进行设计施工,因此本文采用某地下停车场双圆筒螺旋坡道设计数据,在Carmaker中进行道路建模,如图5所示。该螺旋坡道由内外2个圆筒组成,坡道坡度为9%,其内圆筒内壁半径为6 m,外圆筒外壁半径为14 m。螺旋坡道顺时针下降,径向无坡度[16]。
本文选择螺旋坡道平面内某条螺旋线作为已知规划的跟踪路径,如式(9)所示。根据经验选取式(7)中的反馈系数k1=1.2,k2=0.8,智能汽车在地下停车场螺旋坡道低速自主行驶的期望速度为5 km/h,路径跟踪结果如图6所示。
(9)

图5 螺旋坡道三维示意图
4.2 仿真结果分析
图6是智能汽车在地下停车场弯曲坡道行驶路径跟踪的仿真结果。智能汽车在螺旋坡道自上而下低速行驶,以一条已规划的螺旋线路径为跟踪对象,低速行驶的期望速度为5 km/h,车速由智能汽车ESP模块控制。由图6(a)可见,车速能较快地稳定在5 km/h,显然,车速对位置偏差的影响可忽略。
路径跟踪控制器根据车辆实际位置与目标位置的偏差,由非时间参考控制律计算得出方向盘转角。根据式(7),方向盘转角由路径曲率和位置误差所决定。由图6(b)可知:初始位置误差较大,位置误差在控制律中占较大比重,控制律输出较大的转角值。当位置误差逐渐减小时,位置误差在控制律中的占比逐渐减小,控制律输出的转角逐渐由路径曲率控制。因此,方向盘转角逐渐减小到符合路径曲率的转角值上。
由图6(c)和图6(d)可见:在非时间参考的控制律作用下,随着方向盘转角由最大减小到符合路径曲率的转角值上,Y轴偏差逐渐减小并趋于0,航向角偏差也逐渐减小,车辆的位置误差逐渐减小并趋于0。由图6(e)可知:除初始位置偏差控制外,智能汽车在螺旋坡道自上而下低速行驶的跟踪路径与目标路径基本重合。

图6 路径跟踪仿真结果
根据上述仿真结果,当螺旋弯曲坡道的路径跟踪存在初始偏差的情况下,采用非时间参考的路径跟踪控制律能保证系统误差快速收敛趋近于0,并且方向盘角度抖动较小,具有较好的渐进稳定性。
5 结论
1) 提出了智能汽车非时间参考的螺旋弯曲坡道路径跟踪控制方法。智能汽车在低速泊车入库过程中,自上而下的跟踪路径与目标路径基本重合,位置偏差和航向角偏差趋于0。该方法以非时间参考量为因变量,降低了跟踪控制系统对于汽车行驶轨迹精度的要求,具有较好的三维空间路径跟踪效果。
2) 针对在三维空间内位置跟踪的三参数特点,提出以Z轴位置变量为非时间参考的因变量的路径跟踪控制方法,将三维空间位置跟踪的3个参数转化为二维平面位置跟踪的2个参数,降低了路径跟踪控制器设计的复杂度。
3) 采用Carmaker与Simulink联合仿真对路径跟踪控制策略进行验证,Carmaker中车辆模型与实车存在一定差距,建立的道路模型与实际施工建设的地下停车场坡道也不完全一致,下一步的研究将在实际地下停车场弯曲坡道上进行实车路径跟踪控制策略验证。同时将对地下停车场弯曲坡道内障碍物和墙壁的检测、车辆定位方法以及狭小空间避撞控制方法进行研究,以实现智能汽车在地下停车场自主泊车入库和出库。
