剪刀式隔离开关的有限元分析及试验

董洪达，黄 涛，梁晓鸥，王晓伟，宋 爽，葛志成，张赛鹏，陈捷元

(1. 国网吉林省电力有限公司电力科学研究院，长春 130021；2. 南京航空航天大学，南京 210016；3.国网长春供电公司，长春 130021)

隔离开关是变电站中数量最多的一次设备，其中剪刀式隔离开关以其操作的灵活性和快捷性在220 kV变电站中被广泛应用。在运行操作中，由于制造精度不够、动触头过长、使用时间过长等原因会引起隔离开关闭合不到位等故障[1]，隔离开关动、静触头之间接触压力不够，接触电阻变大，从而发生隔离开关异常发热。为了探究隔离开关是否闭合到位，对隔离开关进行在线监控和故障诊断分析，建立分析模型，同时进行动力学测试分析，对模型进行修正，得到和测试结果基本一致的准确分析模型。有限元分析方法建模准确、计算精度高，适合对设备结构进行动力特性分析和响应预测[2]，采用有限元分析方法作为隔离开关的建模分析方法更为切合。本文通过建立剪刀式隔离开关的有限元仿真模型，进行隔离开关模态试验，比较仿真分析与模态试验间的差异，对仿真模型进行修正，最终得到剪刀式隔离开关的准确有限元仿真模型。

1 有限元建模分析

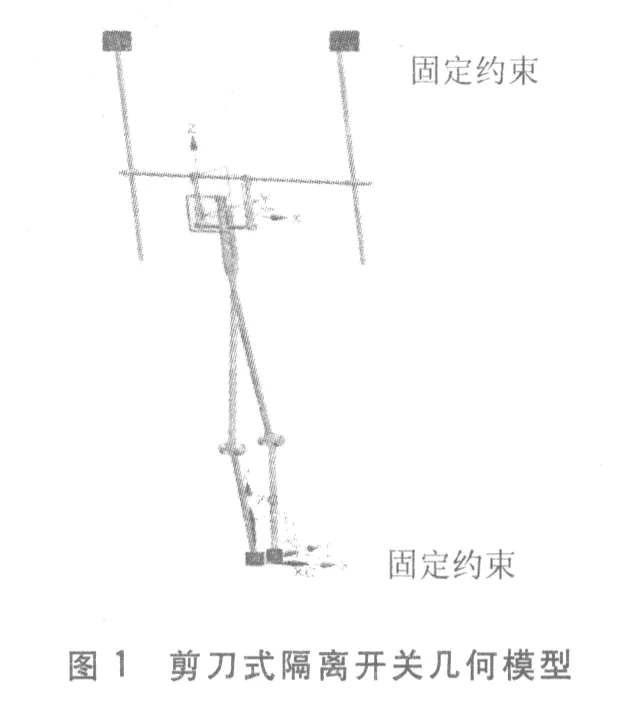
图1 剪刀式隔离开关几何模型

为研究剪刀式隔离开关闭合不到位等问题，对其进行有限元建模分析，以设备结构为基础，建立隔离开关的几何模型，在建模时充分考虑隔离开关的结构参数，使模型尽可能贴近于实际设备。根据剪刀式隔离开关的结构特征和尺寸测量参数，对处于闭合状态的隔离开关建立几何模型(见图1)。几何模型分为动触头和静触头2部分，隔离开关静触头与线路连接部分由于实际结构过大，此处用固定端约束进行代替，隔离开关的动、静触头及连杆均选用管状结构。

以隔离开关的几何模型为基础，对隔离开关进行有限元分析。模型中各部分之间采用刚性连接，在分析时采用实体单元对动、静触头进行网格划分，单元类型选取4面体10节点单元[3]，单元尺寸为8 mm，有限元模型的网格节点参数见表1。

表1 有限元模型网格节点参数

由于隔离开关在运行时，总存在一个或者多个振动频率，故障时，振动频率的频谱特征随之发生变化，因此在分析隔离开关闭合不到位等故障时，需要研究有限元模型的振动频率。

在对模型进行有限元分析时，对隔离开关施加面约束，计算隔离开关的振动频率和振型，得到有限元模型的5阶模态频率和振型(X向、Y向)，其中模型振动频率见表2，有限元模型的模态振型分别对应X向1阶、X向2阶,Y向1阶和2阶，Y向3阶。

表2 有限元模型振动频率

2 模态试验分析

为衡量有限元模型的准确性，对隔离开关进行模态试验，将仿真模型和模态试验结果进行对比，评估仿真模型的准确性并加以修正。

模态分析方法针对由若干部分组成，相互之间无质量、刚性连接的系统进行分析，从而确定其动力学特征[4]。本文通过对剪刀式隔离开关进行合理、有效、可靠的模态试验，获取其固有模态频率、振型等动力学参数，并与仿真模型的计算结果进行对比。

2.1模态试验方法

本次模态试验全部采用单输入多输出(SIMO)的模态试验方法，结合有限元模型对动、静触头的分析过程，对隔离开关进行合理布点，将模态试验分为横向与纵向两部分。在隔离开关各连接部位表面均匀布点，静触头上布置34个测点，动触头上布置32个测点,共计66个测点，传感器布置在第22、33及57号测点上(见图2)。

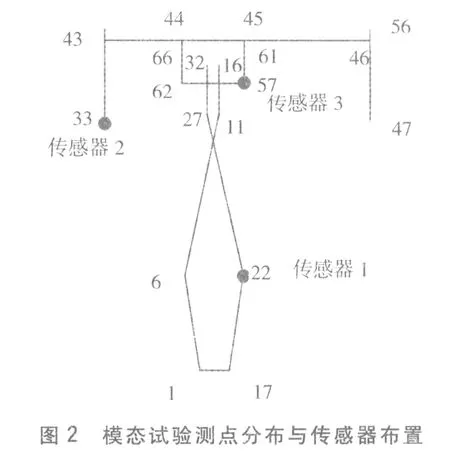
图2 模态试验测点分布与传感器布置

模态试验的激励方式为力锤激励，采用力锤依次对每个测点进行敲击，敲击方向尽量确保沿着径向垂直机匣表面。振动响应的测量方式为，在锤击激励的同时，使用传统的加速度传感器对测点位置进行振动加速度响应测量。模态分析时采用频域方法，即通过动态信号分析仪测量激励点和响应点的时域信号，进行快速傅里叶变换(FFT)，转变成频域信号，计算获取频响函数(FRF)，利用模态分析软件对FRF进行模态参数辨识，获取各阶模态的固有频率、振型等参数。其中，频响函数和模态参数之间的关系如下：

(1)

式中：αlp(ω)为激励点p、响应点l的频响函数；m为低阶残余模态；n为高阶残余模态；ωr、φr、r分别为第r阶模态的固有频率、振型向量和结构阻尼比；φpr、φlr分别为第r阶模态振型向量φr中p点、l点的振型数据；i为修正因子。

将被测隔离开关模型看作为弹性体，并离散化为多个集中质量，对应图2中66个测点。在测量获取频响函数之后，进行模态分析，获取频率、振型，然后按照每个测点的方位角进行分解，将径向激励径向测量的振型数据分解到X、Y方向，与有限元模型计算结果进行对比分析。

2.2 试验结果分析

为了更好地识别结构的模态参数，将每个传感器的测试数据单独分析，相互参考，然后将振型进行合成。在动态信号分析软件中，分析每个测点的测试数据，将3个传感器测点的数据合成对比，得到试验的模态频率和振型(X向、Y向)，其中频率结果见表3，此处列出前2阶测试数据的模态频率，试验的模态振型分别对应X向1阶、X向2阶、Y向1阶、Y向2阶、Y向3阶。

表3 模态试验频率

3 仿真模型与模态试验对比

为评估有限元模型的准确性，将仿真模型和模态试验结果进行对比见表4、表5。由表4、表5可知，前5阶模态的的振型数据能够匹配，但是频率误差阶较大，最大的频率误差是40.97%，模态置信准则(MAC)值也较低，第二阶的MAC值只有0.55。MAC值介于0～1，大于0.9说明两个模态向量有很好的一致性，两阶对应的模态为相关的模态对；若接近0则说明两阶模态向量有较大的差异，不是对应模态。在工程中，若两阶模态的MAC值大于0.6，就可认为二者是相关模态对。由此可见，仿真模型与模态试验结果有较大差异，需要进行修正。

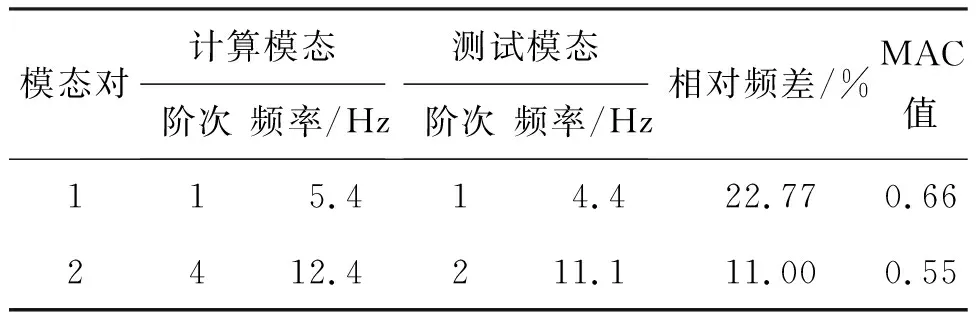
表4 仿真模型与模态试验结果对比(X向)

表5 仿真模型与模态试验结果对比(Y向)

4 有限元模型修正

上述有限元模型与模态试验之间存在较大差异的原因在于该模型是基于剪刀式隔离开关的测量数据建立的，建模过程中存在一定的测量误差，并且隔离开关的材料属性、几何形状、边界条件等均会导致有限元模型的分析结果出现偏差。在对有限元模型进行修正时，可采用直接法和间接法。直接法是通过直接修正有限元的质量或刚度矩阵，该方法简单直接，但通常修正结果缺少实际的物理意义；间接法则需要迭代求解，通过修正结构参数，来调整有限元模型的预测结果与模态试验数据的差异。本文选用间接法对有限元模型进行修正，采用基于灵敏度的迭代修正方法[5]。

在进行有限元模型修正之前，首先将隔离开关的结构划分为8个部分，剪刀式隔离开关拐臂下部、上部为M1、M2，动触头为M3，静触头为M4，静触头连接杆为M5，静触头连接母线为M6，两侧线路为M7、M8。将模型中每部分的弹性模量选为修正参数，在修正前每部分的材料参数均相同，采用基于灵敏度的方法对有限元模型进行修正。

经过模型修正后，仿真模型和模态试验结果对比见表6、表7。由表6、表7可知，经过模型修正后有限元模型的计算频率值精度得到了提高，最大频差仅为8.99%，MAC值也有相应的提高均在0.6以上。由此可知，经过基于灵敏度的迭代修正方法对模型修正后，得到了更为准确的有限元仿真模型；但MAC值仍较低，说明造成仿真模型计算误差的原因不仅仅是模型的材料参数误差，还存在其他的误差。通过对比有限元模型与隔离开关实际结构，发现实际结构的剪刀部位是通过铰链连接的，与仿真模型不同，因此隔离开关铰链结构部分的精确建模需要在以后的研究中加以考虑。

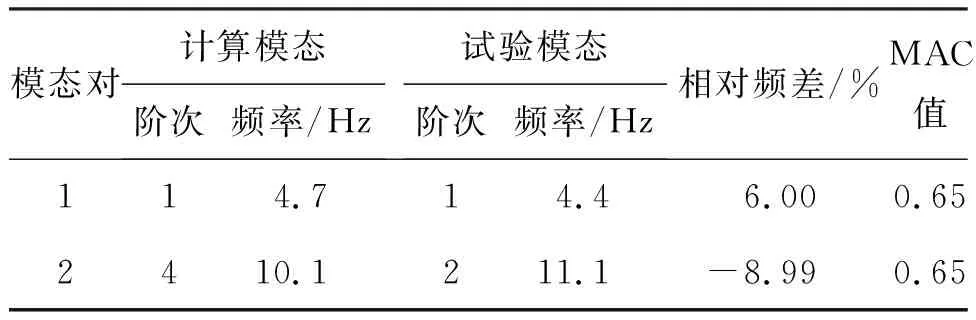
表6 修正后仿真模型与模态试验结果对比(X向)

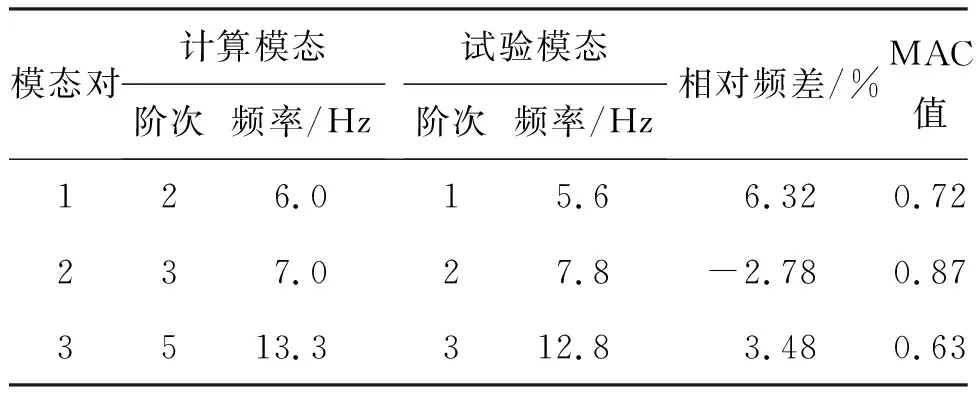
表7 修正后修正后仿真模型与模态试验结果对比(Y向)

5 结论

本文通过在实验室内对剪刀式隔离开关进行测绘，建立了隔离开关的有限元模型，获取该类型隔离开关的前5阶动力学特性；并针对剪刀式隔离开关进行模态试验，将仿真模型计算结果与模态试验结果对比，找出了二者之间的差别；然后采用间接法对仿真模型进行修正，经修正后，有限元模型与模态试验之间差异较小，得到了剪刀式隔离开关准确的有限元仿真模型，为以后剪刀式隔离开关的评估诊断和在线监测提供支撑。