交直流混联系统小扰动稳定性分析

2018-02-21李晨辉

吉林电力 2018年6期

黄冬，李晨辉，孟尧

(东北电力大学，吉林吉林 132012)

电力系统小扰动稳定性分析一直是关系到电力系统安全稳定运行的重要问题。近年来，随着区域电网互联规模不断扩大，基于电压源型高压直流输电(VSC-HVDC)工程数量的增多和传输容量的增大，直流系统和交流系统之间的互相影响，使电力系统小扰动稳定性分析面临新的挑战，因此，改善含VSC-HVDC混联系统的运行方式、提高混联系统的小扰动稳定性成为一个亟待解决的问题。

与此同时，半导体开关器件的性能有了很快的发展。门极可关断晶闸管(GTO)、绝缘栅双极晶体管(IGBT)等全控型电力电子器件的电压源型换流器(VSC)逐步得到广泛应用[1]。VSC-HVDC由于其优越的有功无功独立可控性，自1990年被提出来后，一直吸引着学术界科研工作者的广泛关注[2]。由于釆用了全控器件，VSC-HVDC不需要交流电网提供换相电压，不会出现换相失败[3]，可联结弱电网和向无源网络供电，成为代替传统交流联络线路，联接局部弱电网与主网的一种新选择，为提高系统运行稳定性、抑制低频振荡提供了新思路[4]。

1 混联系统小扰动模型及特征值分析法基础

1.1 VSC-HVDC各状态量关系

小扰动法分析关键在于准确建立反映各个状态量关系的状态函数关系式[5]，得到简便实用的数学模型。国内外很多文献对VSC-HVDC的小扰动模型有很好的参考价值，但在实际分析时，仍要考虑交直流系统间的交互作用。

假定P+jQ是VSC-HVDC系统流向交流系统的功率，Ui(i=1,2)是VSC两端与交流系统连接点处的电压幅值，则可得：

(1)

式中：ΔXac为交流系统的状态量;Aac、Cac为除交直流连接点以外交流系统线性化的系数矩阵；Bac、Dac为交流系统微分方程中交直流系统连接点处的系数矩阵；ΔS为交直流系统连接点处视在功率的状态量；ΔU为交直流系统连接点处电压的状态量。

其中：

ΔS=[ΔPΔQ]

(2)

式中：ΔP、ΔQ分别为系统流向交流系统功率的有功、无功功率状态量。

VSC-HVDC的状态空间模型：

(3)

式中：ΔXdc为VSC-HVDC系统的状态量，ΔXdc=[Δisdref,Δisqref]T,Δisdref、Δisqref分别为交流侧电流的d、q轴电流变量;Adc、Cdc为除交直流连接点以外VSC-HVDC系统线性化的系数矩阵；Bdc、Ddc为直流系统微分方程中VSC-HVDC系统连接点处的系数矩阵。

联立式(1)、式(3)可得：

(4)

式中：ΔX=[ΔXacTΔXdcT]T;A为全系统线性化模型的状态矩阵。

1.2 VSC-HVDC控制器模型

VSC-HVDC系统主要有定直流电压控制、定有功功率控制、定无功功率控制和定交流电压控制。其控制器测量值与给定值进行比较，通过PI调节器进行调节，从而达到相应控制的效果，其控制器框图见图1。

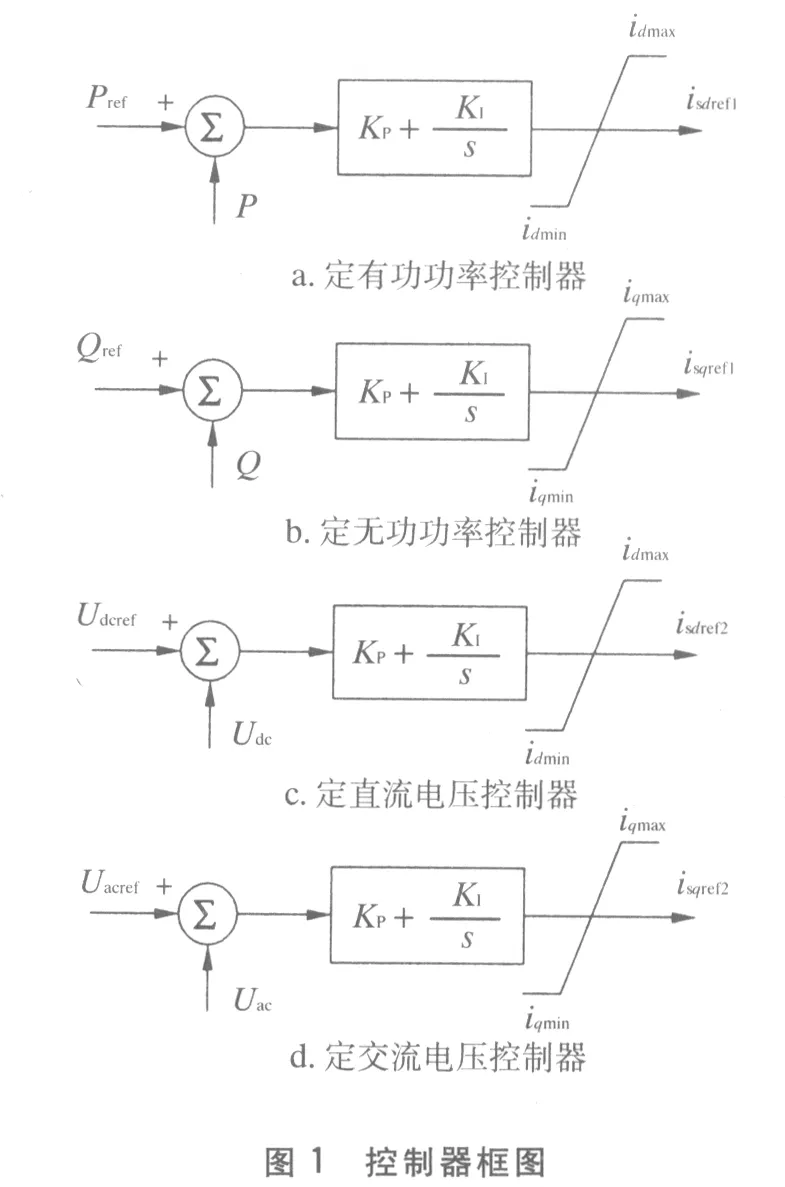
图1 控制器框图

其传递函数框图中P、Q、Udc、Uac为有功功率、无功功率、直流电压、交流电压控制器的测量值；Pref、Qref、Udcref、Uacref均为有功功率、无功功率、直流电压、交流电压的给定参考值；KP、KI为PI调节器设定值；isdref1、isqref1和isdref2、isqref2为交流侧电流的d、q轴电流分量；idmax、iqmax分别为d轴和q轴约电流最大值；idmin、iqmin分别为d轴和q轴约电流最小值。

以定功率控制为例说明控制器的建模方法：

(5)

现引入一个新的状态量MP：

MP=(Pref-P)KI/s

(6)

则可得到状态变量MP时域的微分方程为：

(7)

将公式(6)代入公式(5)可得代数变量isdref1的计算公式：

isdref1=(P-Pref)KP+MP

(8)

同理，定直流电压控制、定无功功率控制和定交流母线电压这3种控制方式分别引入一个新的变量MUdc、MQ、MUs，其时域下的微分方程分别为：

isdref2=(Udcref-Udc)KPUdc+MUdc

(9)

isqref2=(-Qref+Q)KPQ+MQ

(10)

isqref2=(Uacref-Uac)KPUac+MUac

(11)

式中：KPUdc、KPQ、KPUac分别为定直流电压控制、定无功功率控制和定交流母线电压这3种控制方式下的PI调节器设定值。

2 交直流混联系统小扰动分析

目前，针对含VSC-HVDC交直流混联系统的小扰动稳定性问题，国内外科研工作者进行了大量的工作。小扰动稳定性研究的方法[6]通常有：时域仿真法、特征分析法、普罗尼分析法、频域分析法。在电力系统小扰动分析中，与其他方法相比，特征值分析方法可揭示整个系统的动态稳定性，确定系统的弱阻尼或负阻尼模式，并提供特征值与系统参数间的灵敏度，在电力系统小扰动稳定性分析中得到广泛应用。本文分析含柔直系统的交直流混合系统小扰动稳定性的具体步骤如下。

2.1 算例分析

为了探究VSC-HVDC的最佳阻尼运行控制方式，本节采用修改的4机11节点交直流混合系统进行仿真分析，交流系统的具体参数见文献[7]，并对几种运行控制方式进行故障验证，而后求出其灵敏度，验证最佳阻尼运行控制方式具有良好的阻尼特性。

本节采用修改的4机11节点交直流混合系统, 两换流站的阻抗标幺值都设为1，两换流站最大桥臂内电压标幺值设为1.07，无功功率上限取值300 Mvar，下限取值-300 Mvar，交流电压控制斜率取值为0。

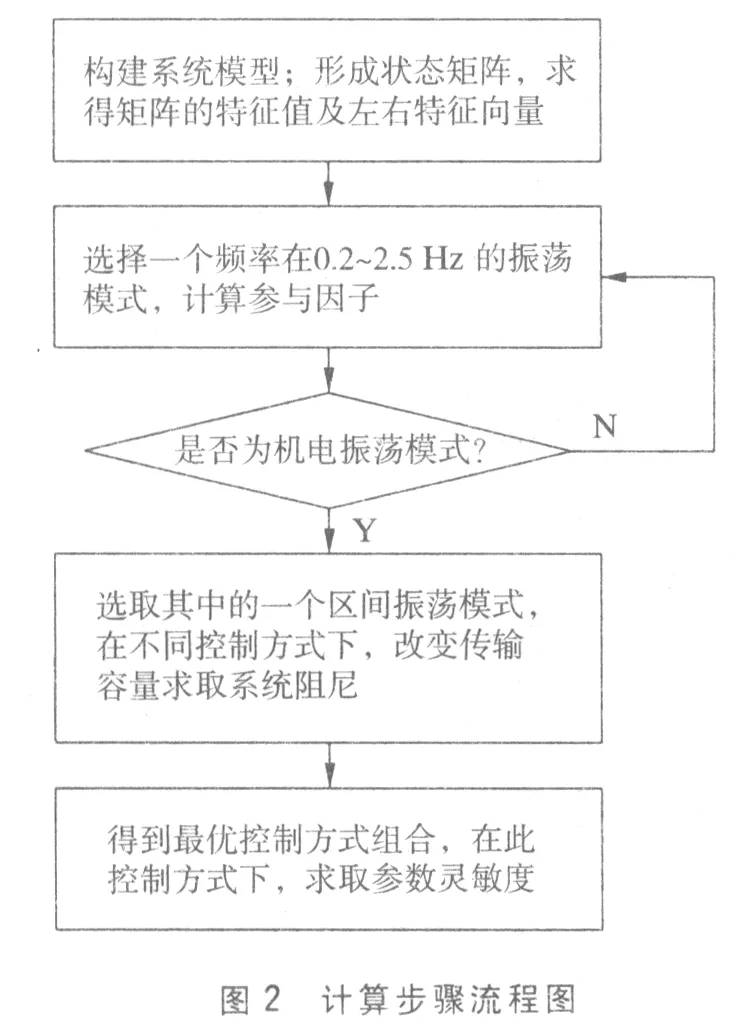
图2 计算步骤流程图

图3 改进的4机11节点系统

2.2 不同运行控制方式对阻尼比和频率的影响

换流站有功类运行控制方式有：定有功功率和定直流电压控制；无功类运行控制方式有：定无功功率和定交流电压控制；根据换流站1、2不同有功、无功功率运行控制方式的组合，有4种不同的情况(见表1)。

表1 换流站1、2的4种运行控制方式

基态下，经过特征值分析，该系统在不同运行方式下，共有3个机电振荡模式，分别为：f1=0.517～0.587 Hz，ξ1=0.009 7～0.046 5的区间振荡模式，在该振荡模式下，发电机1和2与发电机3和4相对运动；f2=1.026～1.063 Hz，ξ2=0.053～0.076为局部振荡模式，该模式下，发电机1与发电机2相对运动；f3=1.008～1.162 Hz，ξ3=0.051～0.072为局部振荡模式，该模式下发电机3与发电机4相对运动。选取该系统区间振荡模式进行分析，不同的柔直运行控制方式下，区域间振荡模式的振荡频率f1和阻尼比ξ1随柔直系统传输功率变化趋势见图4和图5。

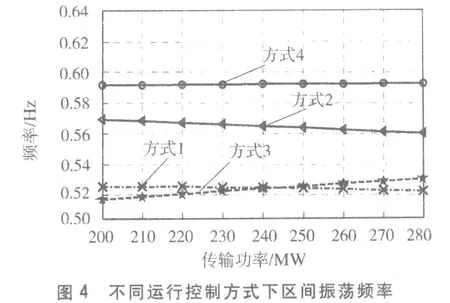
图4 不同运行控制方式下区间振荡频率

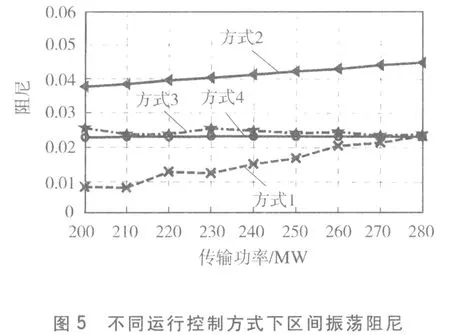
图5 不同运行控制方式下区间振荡阻尼

图4为该区间振荡模式下的振荡频率，由图4可知：方式4的运行控制方式下，在传输功率200 MW时，区域间振荡频率为0.592 Hz，在传输功率为280 MW时，区域间振荡频率为0.594 Hz，系统的区域间振荡随着直流传输功率的增大而略微增大；方式1与方式3的频率较为接近，变化范围为0.559～0.570 Hz；方式2的运行控制方式下，在传输功率200 MW时，区域间振荡频率为0.569 Hz，在传输功率280 MW时，区域间振荡频率为0.560 Hz，系统的振荡频率均随着直流传输功率增大而减小；在直流传输功率从200 MW到280 MW增大过程中，方式4的振荡频率一直大于其他3种运行控制方式。4种运行控制方式的区域间振荡频率变化范围均在0.519～0.595 Hz之间。

图5为不同控制方式下的系统区间振荡模式的阻尼比：在方式2运行控制方式下，传输功率为200 MW时，区域间振荡模式阻尼比为0.039 2；在传输功率为280 MW时，区域间振荡模式阻尼比为0.044 3，系统区域间振荡模式阻尼比随着直流传输功率的增大而增大；方式1与方式3在传输功率为200 MW时，区域间振荡模式阻尼比为0.024 0，在传输功率为280 MW时，区域间振荡模式阻尼比为0.025 0，随着直流传输功率增大，区域间振荡模式阻尼比增大趋势平缓；方式4在传输功率为200 MW时，区域间振荡模式阻尼比为0.009 1，在传输功率为280 MW时，区域间振荡模式阻尼比为0.025 0，随着直流传输功率的增大，区域间振荡模式阻尼比增大趋势显著，该现象表明：适当增大VSC-HVDC所传输的有功功率可有效提高系统区域间低频振荡的阻尼比，改善系统的动态稳定性。

在直流传输功率为200 MW时，4种运行控制方式的阻尼分别为0.024 0、0.039 2、0.024 0、0.009 1；在直流传输功率为280 MW时，4种运行控制方式的阻尼分别为0.025、0.044 3、0.025 0、0.025 0；在直流传输功率从200～280 MW增大过程中，方式2即在换流站1定有功功率和定交流电压，换流站2定直流电压和定无功功率的阻尼一直大于方式1、3、4，而方式1、3、4的阻尼值较为接近，反映了在区间振荡模式下，同一传输功率，不同运行控制方式中，方式2即换流站1定有功功率和交流电压，换流站2定直流电压和无功功率运行控制方式的系统阻尼特性最好，为最佳阻尼运行控制方式。

2.3 故障分析

对运行控制方式2进行故障验证。以发电机1为参考机，5 s时母线10、11相连的线路发生三相短路，短路持续时间0.1 s，即在时间5.1 s时短路故障切除。不同运行控制方式下，发电机3的转子角振荡曲线见图6。

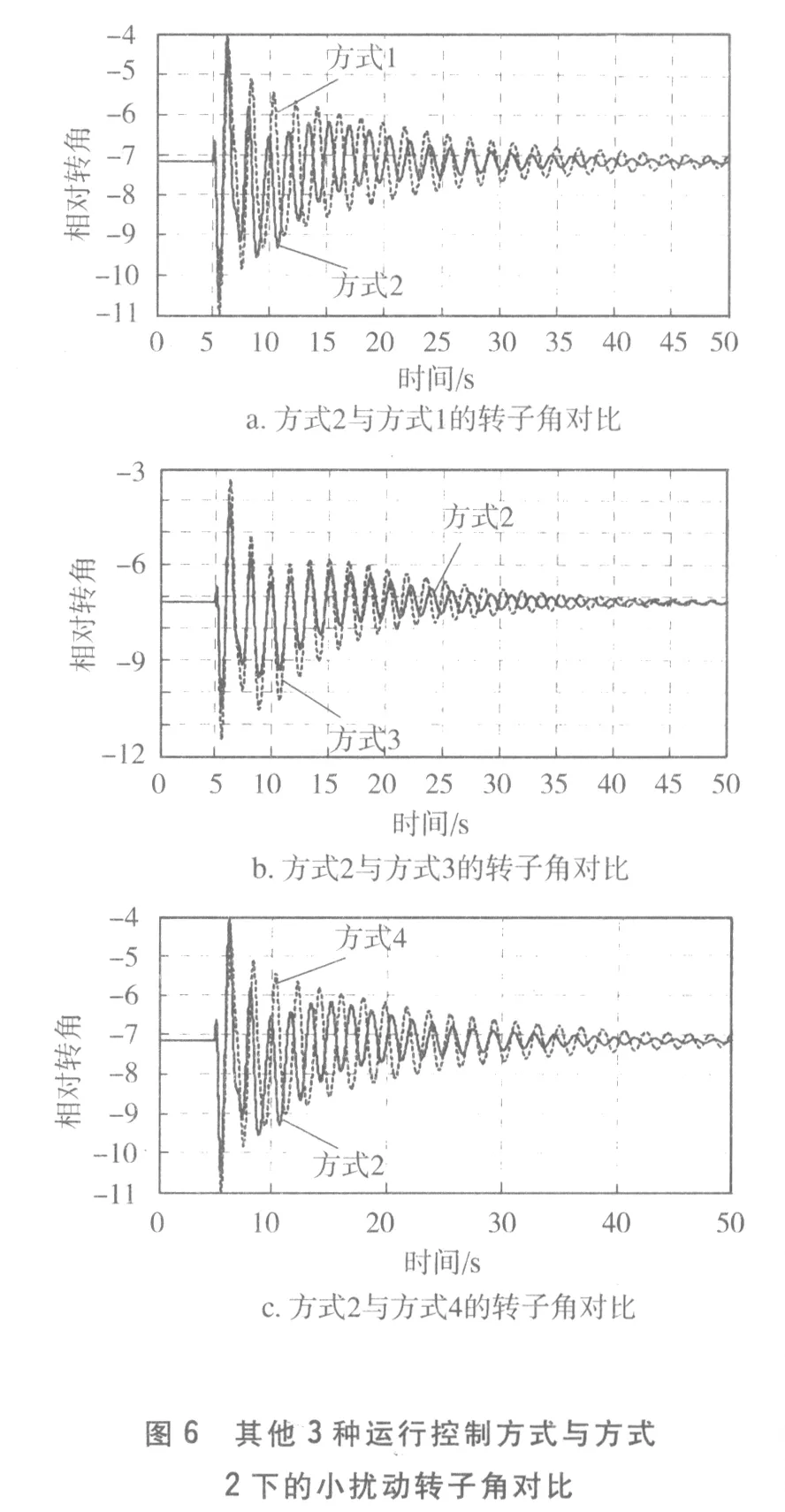
图6 其他3种运行控制方式与方式2下的小扰动转子角对比

由图6可见，在5 s时系统发生扰动，各种柔性直流系统运行控制方式下，发电机转子角均发生摇摆，切除扰动，仿真持续到50 s时。方式2下的相对转子角恢复稳态，持续到55 s时方式1、3、4下的相对转子角才恢复稳态；发生扰动后，方式1、2、3、4的转子角幅值超调量分别为44.7%、41.8%、44.9%、42.1%；在方式2下，系统恢复至稳态的时间最短，超调量最小，反映了采用方式2运行控制方式，系统具有良好的区域间振荡阻尼特性。

2.4 灵敏度分析

进一步对区域振荡模式阻尼比对直流参数的灵敏度进行分析。方式2运行控制方式下，改变直流传输功率，计算区域振荡模式阻尼比对柔性直流系统参数的灵敏度。在保持换流站交流换流母线电压为定值，不同直流传输功率下，区域间振荡模式阻尼比对交流换流母线电压的灵敏度见图7a；在保持换流站无功功率为定值，不同直流传输功率下，阻尼对换流站定无功的灵敏度见图7b；在保持换流站直流电压为定值，不同直流传输功率下，阻尼对直流电压的灵敏度见图7c。