基于e-σ修正的自适应控制器及容损飞行验证*

程鹏飞,苗昊春,张 宝,吴成富

(1 西安现代控制技术研究所,西安 710065;2 西北工业大学无人机特种技术重点实验室,西安 710065)

0 引言

近年来,自适应控制的理论和算法体系框架在深度和广度上的推导与综合不仅力求严格遵守稳定性理论,而且在工程上较其他先进控制算法更加快速的朝着工程实用方向发展[1-5]。当飞行器发生舵面卡死甚至是遭受严重的非对称损伤时,传递函数会发生众多本质性的改变,而传统PID控制器对这些变化的适应能力将明显不足。近年国内外部分院校的学者在传统σ修正律、e修正律的模型参考自适应控制(model reference adaptive controller,简称MRAC)基础上不仅继续对自适应容错姿态及轨道控制进一步深入探索[6-9],而且对系统镇定/跟踪过程中暂态性能的提升做出了贡献[10-11]。文中首先给出e-σ修正混合自适应律模型参考自适应飞行控制算法的简要设计过程。最后通过接入航点绕飞制导律,给出控制突发单侧机翼大面积损伤飞机快速稳定和性能恢复过程的试飞验证结果。

1 鲁棒模型参考自适应控制方案

1.1 控制结构

MRAC闭环控制方案由指定好参数的参考模型系统、控制给定组成的前馈信号部分、系统输出组成的反馈信号部分、以及控制参数更新律(自适应律)组成。控制参数受到更新律的调节,改变控制量并最终使得变参数系统的输出跟踪参考模型的输出。

1.2 改进的e-σ修正混合自适应律

为了进一步减小上述传统更新律下的控制参数误差和系统输出误差界限值,提出e-σ修正混合自适应律,下面分别简要给出在外部扰动和未建模动态下改进自适应律的方法和性能分析,详细的推导证明和数字仿真见文献[12]。

1.2.1 外扰情况

σ1>0

(1)

2σ2)φTθ*-(2σ1|e1|+2σ2)φTφ

(2)

(3)

a≤‖e‖≤b

(4)

(5)

(6)

R.W. Cooke 和 G. Price[18]将试验桩压入超固结的伦敦黏土中，并测试了沉桩后桩周土体的变形规律，没有进行土压力的测量.张忠苗等[19]在静压预应力混凝土开口管桩试验场地中央和防挤沟两侧埋设了6个土压力计，并在桩端安装了土压力计，成功测试了静压开口管桩沉桩过程中桩端及桩周一定距离土体中径向土压力的变化情况.

(7)

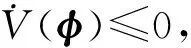
(8)

∃(σ1|ε1|+σ2)>0

(9)

σ1>0,σ2>0

(10)

1.2.2 未建模动态情况

2 综合自适应制导与控制算法系统

图1为基于e-σ修正输出反馈型MRAC的综合自适应制导与控制算法系统框图。前端外环制导算法系统由纵向PID高度制导式(11)、横向PD航线跟踪制导式(12)和式(13)、偏航角ψ制导组成。其中dy为飞机距离当前航线的地面投影有符号垂向距离,Vcrosstrack为垂直于航线方向的速度分量在地面的投影。后端内环姿态控制算法系统由俯仰角控制、滚转角控制和偏航角控制组成。俯仰角控制通道由PID实现,滚转角和偏航角控制通道由1.2节e-σ修正自适应棒输出反馈MRAC算法实现,在此不再赘述。

(11)

φc=Kdy·dy+Kvct·Vcrosstrack

(12)

(13)

3 试飞验证

3.1 飞行验证系统

图2为试飞验证平台系统设备实物图,主要分为载机平台部分和地面站终端部分。图中红色部分为40%面积矩损失的残翼,试飞时在空中突然抛离所用。载机平台内部还具备制导控制计算机、空速管、航姿传感器、舵机、GPS定位、数据链天线、电池,以及应对突发情况的应急降落伞。地面站终端包含运行地面站软件的笔记本、数据链天线基站、差分GPS地面设备组件以及2.4 GHz频段无人机遥控器。

3.2 试飞场景

图3为飞行航路示意图。未损伤无人机从图示中的0号点开始滑跑起飞,随后飞机在基本制导控制算法下一次依次飞过1至4号航点。过4号点后切进所设计的综合自适应航线制导与姿态控制算法系统。切换成功大约5 s后抛离右外翼40%面积矩部分,损伤飞机继续保持稳定姿态并朝着5号点重新进行航线绕飞,直到飞过6号点并定高平飞稳定后结束。

3.3 试飞结果

图4为40%面积矩右翼瞬间抛离后无人机在控制系统的作用下的飞行画面。可以看出在很短的时间内就成功完成了“折翅过程”。分离后,飞机短时间内发生恶性滚转,但随后在自适应控制系统的调整下很快阻止了翻滚并成功改平飞机,最后继续稳定飞行。

下面结合实际的试飞数据进行分析。图5为标有关键事件点的整个3D飞行航迹图,图6为对应的飞行全过程相关状态曲线。无人机在8 000拍(1拍5 ms)左右从传统PID算法成功切换成了综合自适应制导控制算法系统,在9 000拍左右成功实现右翼40%面积矩抛离动作。图6(a)中可以看出,抛离后φ瞬间恶性滚转到76°,但很快就改回姿态。同时从图7中看出,稳定后的航迹与航线方向存在固定偏差角。从理论上讲,这个偏差角的出现不仅跟相比损伤前,损伤后机体传递函数出现的未建模动态有关,而且与自适应增益值的大小相关。另外由于损伤导致机体过弯能力不足,出现了过弯半径较大的现象。

图6(c)中,滚转控制通道的控制参数向量θφ在机体遭遇严重损伤后增加了学习速度,出现了一个峰值,目的是通过控制参数智能且快速调整实现快速打舵,从而迅速补偿损伤带来的巨大机体动力学误差导致的恶性滚转。图6(d)中,左副翼adal在损伤发生后通过自适应学习迅速改平机体。可以看出,之所以在左副翼出现饱和时仍旧能够成功的稳定和过弯,是因为与此同时外环航线制导算法出侧滑角所致。

4 结论

文中提出了基于e-sigma修正自适应律控制器,并在扰动和未建模舵动态下,针对相对阶等于1和大于1的传递函数,严格证明了有界稳定。在此基础上又提出改进后混合自适应律中自适应增益选取的策略。通过试飞验证了该控制器在实际有限舵偏限制下,能有效的对单侧机翼大面积损伤飞机进行快速稳定、性能恢复并使之继续航点绕飞。理论有效性和工程成熟度得以验证。