某型迫弹半爆弹射程偏近原因分析*

孙 浩,马 骏,关艳军

(中国华阴兵器试验中心,陕西华阴 714200)

0 引言

在某型无人飞行器系统设计定型试验中,需要射击某型迫击炮远程杀伤榴弹,每次实弹射击之前,都先射击2发改装的半爆弹来指示落点大概范围。从连续3天的射击结果来看,半爆弹落点比实弹落点普遍偏近200 m左右,下面仅列举其中一天的相关数据,如表1所示。

表1 实弹和半爆弹数据对比

注:质心位置指质心在弹丸几何轴线上的投影点到弹底的距离;表中*代表某数。

从表1中数据可以看出,两种弹药在装药号、弹重、初速和射角等参数方面基本相同,唯独质心位置偏差较大,半爆弹的质心位置相比实弹下降约0.038 m。因此,分析射程偏近原因应主要从改装前后弹丸特征量的变化对外弹道的影响入手。文中研究思路是在质点弹道模型的基础上,对弹道方程进行改进,并利用实测落点数据对弹道模型进行修正,仿真分析实弹和半爆弹在特征量参数方面的差异对射程和飞行攻角等弹道参数的影响,并探讨避免半爆弹出现射程偏近的对策措施。

1 弹道模型建立

尾翼稳定弹丸主要是通过外形设计将飞行中的空气压力中心移到质心的后面,于是空气阻力对质心形成的阻力矩是一个稳定力矩,它力图使章动角减小,这种稳定也叫静态稳定[1-3]。根据迫击炮外弹道特点,结合外弹道学相关知识,经典的迫弹质点弹道模型有如下基本假设[2]:

1)迫弹为理想的轴对称体,无旋转运动,在整个飞行过程中攻角为0;

2)气象为标准气象,无风雨;

3)地表面为平面,重力加速度g垂直于地面,大小恒为9.8 m/s2;

4)忽略地球自转引起的科氏加速度。

自然坐标系是取跟随弹丸质心运动的方向为切线方向τ,而垂直的方向为法线方向η,如图1所示。

在基本假设条件下,迫弹飞行轨迹是一条在射击平面运动的理想弹道,此时迫弹只受重力和空气阻力影响,可得以时间为自变量的运动方程组[4-7]:

(1)

初始条件:t=0,x=y=0,v=v0,θ=θ0。

方程组中:C为弹道系数,C=id2/m×103;H(y)=(1-0.000 021 905y)5.4,0≤y≤9 300 m;F(v)=4.732×10-4ν2Cx(Ma);i为弹形系数;Cx(Ma)为弹丸空气阻力系数;v为弹丸飞行速度(m/s);g为重力加速度(m/s2);t为弹丸运动时间(s);y为弹丸射高(m);x为弹丸水平射程(m);θ为弹道射角(rad)。

实际上迫击炮弹在飞行过程中不可能攻角为0,即弹轴与速度矢量不重合,而是随着飞行速度和飞行位置变化而变化。于是,弹丸由于迎气流面积变大,空气的阻滞作用加强,在这种情况下空气总阻力加大,空气对弹丸作用力的合力不再与弹轴共线反向,其作用点即压力中心以速度矢量为准,向弹顶一方偏离,如图2所示。

(2)

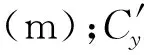
在有攻角存在的情况下空气阻力系数有[1]:

Cx(Ma,δ)=Cx0(Ma)(1+Kδ2)

(3)

式中,Cx0为攻角为0时的空气阻力系数,实际计算中可以采用差值法编写空气阻力系数查表子程序来获得;K为攻角系数,在亚音速条件下,通常取21.1[8]。

将弹丸等效为刚体,根据刚体平面运动特点及力的平移定理,把作用于压心的升力平移到质心,则同时附加一个绕质心的力偶,这个附加力偶的矩就等于平移前升力对质心的矩,即稳定力矩。弹丸在飞行过程中主要靠稳定力矩作用使弹丸绕着质心转动,其微分方程如下:

(4)

式中:JC为弹丸赤道转动惯量(kg·m2);δ为攻角(rad);MC为稳定力矩(N/m)。由于迫弹飞行过程中不旋转,因此稳定力矩主要是由空气阻力的垂直分量即升力产生的,升力可按下式计算[1]:

(5)

则稳定力矩可推导为:

(6)

将公式(2)和(6)带入公式(4)可得:

(7)

根据式(7)即可计算出全弹道攻角变化情况。切向阻力Rx又称迎面阻力,考虑到攻角时有[1]:

0.473 7×d2H(y)ν2Cx0(Ma)(1+Kδ2)

(8)

进而可得到存在攻角的条件下,沿飞行方向的加速度计算公式:

(9)

将公式(2)代入公式(5)可进一步推导为:

(10)

进而可得到存在攻角条件下,沿飞行法线方向的角速度微分方程:

(11)

至此,可得到将攻角、阻力臂和赤道转动惯量等参数引入弹道计算的改进弹道模型如下:

2 弹道仿真对比分析

根据推导的弹道微分方程组(12),运用Matlab/Simulink仿真软件进行外弹道模拟仿真,并采用插值法编写空气阻力系数Cx0的查表子程序,仿真程序如图3所示。

2.1 阻力臂对弹道的影响分析

2.1.1 通过迭代仿真求取实际阻力臂

因为阻力臂无法用公式计算求出,因此可将阻力臂设为常量,通过实测落点数据进行迭代仿真逼近,确定近似的阻力臂值,然后将质心后移导致的阻力臂缩短值带入仿真,检验落点变化情况。迭代仿真之前先分析临界稳定的阻力臂,将阻力臂从0.01 m开始逐渐增加,仿真结果如图4所示。

可见,当阻力臂过小时,弹丸将出现明显的飞行不稳定现象。下面通过迭代仿真求取该型迫弹的实际阻力臂,阻力臂h从0.05开始逐渐增加,求取实际阻力臂的迭代仿真弹道曲线如图5所示,迭代仿真结果如表2所示。

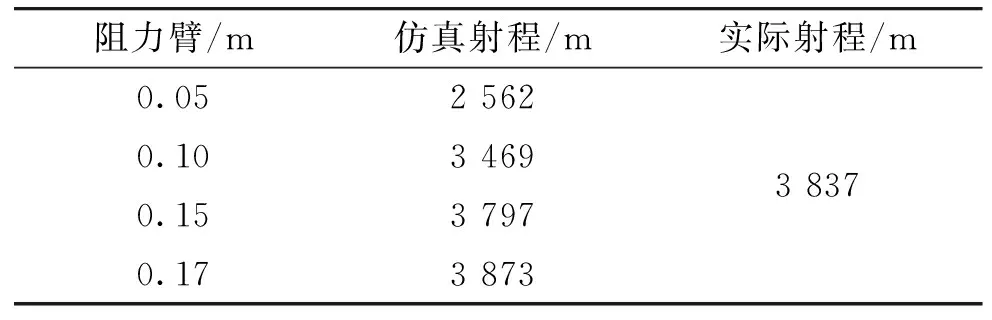
阻力臂/m仿真射程/m实际射程/m0.052 5620.103 4690.153 7970.173 8733 837

仿真结果显示实际阻力臂约为0.16 m,而且从图4和图5中可以明显看出阻力臂越小,射程越小。

2.1.2 阻力臂影响射程的机理分析

下面单从阻力臂角度分析半爆弹射程偏近的原因,假定实弹改装成半爆弹后,质心位置下移0.038 m并未引起赤道转动惯量的显著变化,但是造成阻力臂减小0.038 m,实弹(h=0.16 m)和半爆弹(h=0.122 m)的弹道仿真结果对比如图6所示。

仿真结果显示,阻力臂缩短0.038 m造成了理论射程偏近190 m,与实际射程偏近程度相当。为全面了解半爆弹和实弹在整个飞行过程中的相关参量变化,分别得到了飞行速度对比如图7所示、攻角对比如图8所示、飞行阻力对比如图9所示。

可见,由于质心后移0.038 m导致的阻力臂缩短直接造成稳定力矩减小,整个弹道过程中飞行速度、弹道倾角、攻角等过程参数都发生变化,特别是飞行中攻角的普遍增大,使飞行阻力增加,最终导致射程偏近较大。

2.2 赤道转动惯量对弹道的影响分析

该批迫弹实弹的平均赤道转动惯量Jc=0.033 17 kg·m2,为分析改装前后赤道转动惯量变化对弹道的影响,设定赤道转动惯量依次变化0.003 kg·m2,同时保证初速、射角、弹重、阻力臂等参数不变,可得在不同赤道转动惯量情况下的理论弹道曲线,如图10所示。

从图10可以看出,赤道转动惯量越小射程越大。同时,根据赤道转动惯量定义可知:弹重的变化会直接影响弹丸的赤道转动惯量,因此,通过改变弹重来影响射程从理论上分析是可行的。

2.3 避免半爆弹射程偏近的对策分析

从2.2中的分析可知,如果弹丸装填时通过改变弹重使赤道转动惯量减小,就会提高射程。因此,文中利用已有试验条件对1发该型迫弹进行反复装填和测量实验,装填时尽量不改变原有装填密度,相关实测数据如表3所示。

表3 某型82迫砂弹装填数据对比表

注:表中*代表某数。

可以看出弹丸质量每降低100 g对应质心位置增大4 mm左右,对应赤道转动惯量要减小0.8×10-3kg·m2。将数据代入弹道方程进行仿真,结果如图11所示。

可见,随着弹丸质量的逐渐减少,射程逐渐增加,当弹丸质量减少了200 g时,比实际射程近104 m。当减小了300 g时,比实际射程只近62 m,而且并未影响飞行稳定,只是弹道高相比实弹要大,可见该方法是可行的。

3 结论及建议

1)造成该型迫弹半爆弹射程偏近的主要原因是质心位置后移导致的阻力臂缩短幅度较大,而阻力臂的缩短又促使全弹道攻角普遍增大,飞行阻力增加,最终影响到射程,如果阻力臂缩短到一定程度后,还会严重影响飞行稳定性。

2)该型迫弹的质心位置和赤道转动惯量两个参量中,质心位置对飞行稳定性和射程影响最大,赤道转动惯量次之。

3)为避免该型迫弹半爆弹出现射程偏近,可采取两种措施:一是改装半爆弹时,不是靠压缩填料而是靠减少填料来为炸点指示剂预留足够的空间,以此来减小弹丸赤道转动惯量,最终提高射程。二是改进炸点指示剂,可尝试使用压制成型的炸点指示剂,成分接近曳光剂和烟幕剂,在保证产生足够强度的指示效果的前提下,尽可能减小弹丸头部预留装填空间,保证改装前后质心位置变化不大。