基于有限时间速度障碍法的UAV避障研究*

杨秀霞,华 伟,孟启源

(1 海军航空工程学院控制工程系,山东烟台 264001;2 海军航空工程学院研究生管理大队,山东烟台 264001)

0 引言

无论是在军事领域还是民用领域,UAV也都得到了广泛应用[1-8]。为了保证UAV的运行安全,UAV需要通过自身携带的机载传感器对周围的飞行环境和其他飞行器的运动状态进行实时感知和判断,并作出合理的机动进行避障。

近年来,针对UAV的自主避障问题,国内外许多学者进行了相关研究,这些方法包括势场法[9],导引法[10-11],微分几何法,随机搜索算法和速度障碍法[12]等等。文献[9]通过改进的人工势场法避免了传统人工势场法易陷入局部陷阱的问题,实现了多机动态航路规划,文献[10]通过确定UAV和障碍物之间的相对位置和相对速度关系确定最优避障速度向量,并将相对速度导引至避障向量上实现避障,文献[12]通过建立速度障碍锥,并将UAV速度偏转出速度障碍锥完成实时避障,但是上述算法都没有考虑碰撞发生时间,因此在速度障碍法基础上,文中提出了一种基于有限时间速度障碍法的避障方法。

1 UAV运动学模型的建立

(1)

式中:X=[x,y,vu,σu]T,x和y、vu、σu分别为UAV在二维平面内的坐标、速率和方向角;u为UAV的控制输入。在实际仿真应用中,通常将UAV的连续运动学模型进行离散化,UAV的离散状态方程为：

(2)

式中ΔT为仿真步长。动态障碍物的运动学模型可同理得到。由于UAV的运行环境是实时变化的,因此UAV需要通过自身携带的机载传感器对周围的飞行环境进行实时感知和判断,UAV的实时避障工作原理图如图1所示。

图1 UAV避障工作原理框图

2 速度障碍法的原理

如图2所示,根据UAV和障碍物之间的相对位置和相对速度关系,如果相对速度位于相对障碍锥内(图中阴影部分),那么经过一段时间之后,UAV与障碍物之间就可能发生碰撞,为了进行避障,需要将相对速度偏转出障碍锥。

如图2所示,障碍锥可由相对障碍锥顶点坐标pu,开口方向q,夹角大小γ三个参数进行表示。

(3)

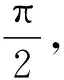
但是通常情况下都希望通过UAV速度矢量来进行碰撞判断,并进行相应的机动实现避障,为此Fiorini和Shiller[12]在20世纪90年代提出速度障碍法(velocity obstacle,VO),作为一种一阶避障方法,在进行避障时,该方法将障碍物的位置和速度同时考虑在内,比较好地解决了动态环境下UAV的避障问题。如图3所示,将相对障碍锥移动矢量vo,即可得到绝对速度障碍锥(阴影部分),如果UAV的速度矢量vu落于速度障碍锥内,说明经过一段时间之后,UAV与障碍物之间会发生碰撞,通过将UAV的速度矢量偏转出速度障碍锥,即可实现避障。

图2 基于相对速度和相对位置的UAV避障示意图

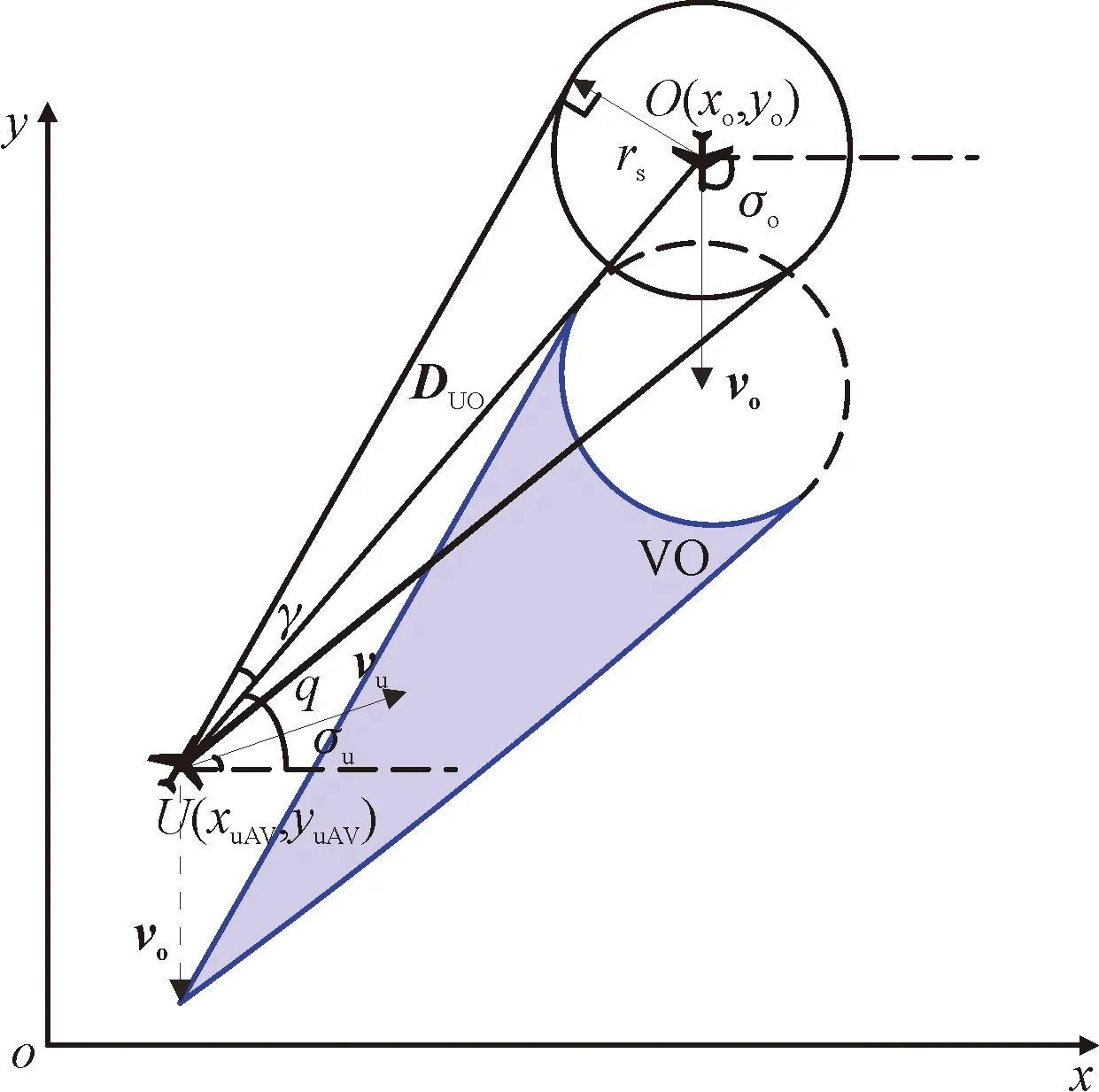
图3 速度障碍法(VO)示意图

对于飞行器U,由障碍物O诱发形成的速度障碍锥VOU|O可定义为：

VOU|O={v∃t>0,pu+(v-vO)t∈⊙(pO,rs)}

(4)

式中:pu为UAV的位置坐标;v为UAV的任一速度矢量;po、vo分别为障碍物的位置坐标和速度矢量,⊙(po,rs)表示以po为圆心,rs为半径的圆域。

3 速度障碍法的改进

通过前文的描述,速度障碍法将所有会导致碰撞的速度都排除在外,即使要经过很长一段时间,碰撞才会发生,这就造成了UAV可选避障速度向量范围的减小,甚至是避障失败。为了克服这一问题,文中在此基础上考虑碰撞发生时间,假设飞行器以某一速度运行,该速度位于速度障碍锥内,飞行器与障碍物之间存在碰撞危险,但是要经过很长一段时间,碰撞才会发生,在这种情况下,为了避免不必要的机动,仍然可以将该速度作为避障速度,为此提出有限时间速度障碍锥(finite time velocity obstacle,FVO)避障方法。

图4 有限时间速度障碍法示意图

如上图所示,对于飞行器U,由障碍物O诱发形成的有限时间速度障碍锥(阴影部分)可定义为:

FVOU|O={v∃t>0且

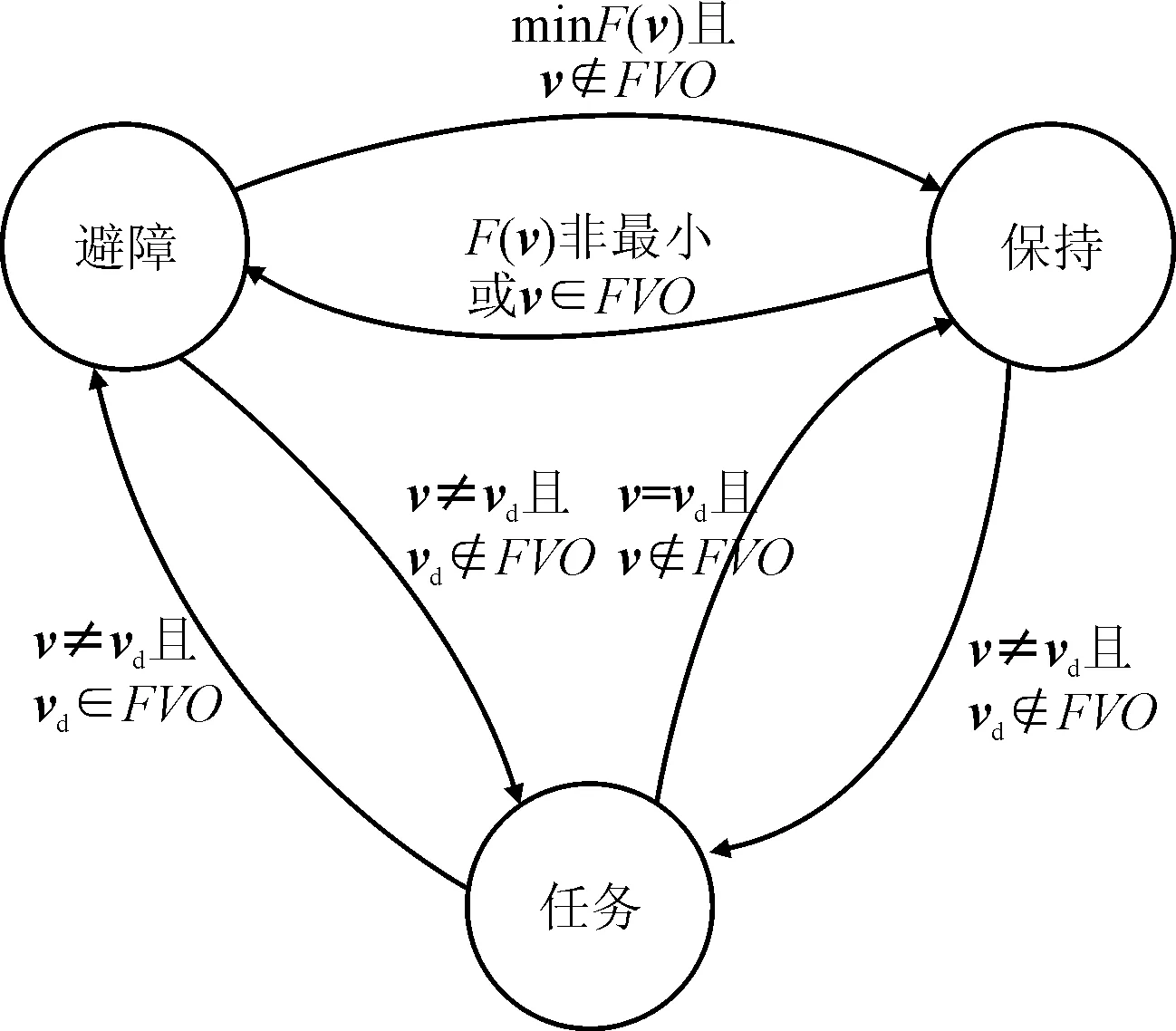
t≥ts|pu-po+(v-vo)t|

(5)

式中：ts为最小允许碰撞发生时间,即飞行器以速度v运行,至少经过ts才会发生碰撞,在此之前,飞行器可以保持当前速度继续运行,这样就为飞行器提供了更大范围的可选避障速度向量范围。

4 基于FVO的最优避障速度选取

通过前文的描述可知,尽管通过有限时间速度障碍法,UAV的可选避障速度向量范围变大了,但是上述方法仍将速度范围简单的化为碰撞速度(collision velocity)和无碰区域(collision-free velocity),为了选择最优避障速度矢量,本节通过设立一系列评价指标来对UAV的待选避障速度矢量进行评价,从而确定最优避障速度矢量。通过选择期望速度,UAV与障碍物之间的相对垂直距离,经过障碍物的时间三个变量作为评价指标来确定UAV的最优避障速度[13]。

4.1 期望速度vd的评价函数

如图5所示,假设UAV的目标点位置已知,那么UAV的期望速度vd的方向为UAV当前位置指向目标点的方向,期望速度的评价函数可表示为：

f1=kv|vd-v|

(6)

式中v为待选的避障速度矢量。

4.2 经过时间tp和相对垂直距离dv的评价函数

相对垂直距离dv定义为UAV与障碍物之间的相对位置向量到相对速度的垂直距离,如图5所示。

图5 期望速度、经过时间和相对垂直距离示意图

由图5可知:

vrel=vo-vu

(7)

dv越小,意味着障碍物的危险程度越高,因此关于相对垂直距离dv的评价函数可定义为：

(8)

经过时间tp可定义为UAV与障碍物之间距离最小的时间,如果UAV与障碍物之间会发生碰撞,那么经过时间就变为碰撞时间,tp可由下式得到：

(9)

从式(19)可以看出,tp有可能是负的,当tp为负值时,说明UAV已经经过了障碍物。同样的,tp越大,说明障碍物的危险程度越低,因此关于经过时间tp的评价函数可定义为:

(10)

但是当相对垂直距离足够大时,即使经过时间较小,对UAV来说,障碍物的危险程度也是较小的。同样的,当经过时间足够大时,即使相对垂直距离较小,对UAV来说,障碍物的危险程度也是较小的,因此为了对障碍物的危险程度进行更加客观的评价,应该同时考虑UAV与障碍物之间的相对垂直距离和经过时间。修正后的评价函数可定义为：

(11)

式中k=k1k2。

最终,总的评价函数可定义为：

F(v)=f1+f2

(12)

f1和f2的权重可以通过选择适当的系数来进行调整。kv越大,说明UAV越倾向于趋近目标,同样的,k越大,说明UAV越优先进行避障。

在UAV运行过程中,可将UAV的运行状态分为避障机动,匀速保持和执行任务三个状态,UAV的三个运行状态之间的转换示意图如图6所示。

图6 UAV运行状态转换示意图

5 仿真验证与分析

假设UAV在二维平面内运行,UAV和障碍物的初始条件如表1所示。

表1 UAV与障碍物初始条件

UAV与障碍物均假设为安全半径为r=1.5 m的圆,最大允许碰撞时间为ts=5 s,仿真步长ΔT=0.1 s,UAV的目标点坐标为(-10 m,-10 m)。

根据有限时间速度障碍法进行判断可知,如果UAV保持当前运动状态,那么经过一段时间之后,UAV与障碍物之间有可能会发生碰撞,为此需要采取一定的机动措施进行避障。在仿真过程中,根据最优避障速度矢量选取原则,实时确定UAV的最优避障速度矢量方向,并在UAV的最大加速度约束范围内将UAV的速度矢量尽快导引至最优避障速度矢量上,从而完成避障。基于有限时间速度障碍法的避障过程示意图如图7～图10所示。

图7 UAV和障碍物初始状态示意图

图8 UAV躲避障碍物1示意图

图9 UAV躲避障碍物3示意图

图10 UAV躲避障碍物2示意图

图11 UAV与各障碍物之间相对距离曲线

通过图11可以看出,在UAV运行过程中,UAV与障碍物之间的相对距离总是大于最小安全半径,说明了文中提出的避障方案能够保证UAV运行过程的顺利避障和运行安全。

6 结束语

针对复杂动态环境下UAV的多障碍物避障问题,文中在速度障碍法的基础上,将碰撞发生时间考虑在内,提出了有限时间速度障碍法,通过设计一系列指标函数,在UAV运行过程中,实时确定UAV的最优避障向量,仿真结果验证了所提出的避障方法的可靠性和有效性。文中提出的避障方法具有良好的适应性,可为UAV的现实避障应用中提供一定的理论依据和借鉴意义。