某型导弹折叠舵动力学仿真与可靠性分析*
2018-02-21王国超金明鑫刘永寿
王国超,李 瑞,程 迁,金明鑫,刘永寿
(西北工业大学力学与土木建筑学院,西安 710072)
0 引言
导弹作为一种现代的高科技战略武器,被广泛的应用于国防装备中。折叠机构用于缩小导弹的横向尺寸,便于箱筒式贮装、发射,扩大车辆、舰艇和飞机的运载能力,提高装备的综合作战效能[1]。折叠展开机构在导弹系统中占据着非常重要的地位,其工作可靠性的高低,关系到能否使处于折叠状态的翼、舵快速展开到位,并准确、可靠的锁定,对导弹发射的成功与否起着决定性的作用。
针对某型折叠舵,虚拟样机仿真软件如Adams,可以在多个随机因素影响下,对折叠舵展开机构进行多次试验仿真,进而对展开机构进行工作可靠性评估与分析。折叠机构的结构及工作环境复杂,失效模式多样、失效机理复杂,经典的可靠性分析方法较难满足折叠舵展开机构工作可靠性分析要求[2]。目前,折叠机构的动力学和可靠性研究工作尚不完善,国内这方面的研究主要有:张钦等以无人机折叠翼为研究对象,得到机翼展开角度、角速度、角加速度和冲击载荷曲线[3]。李东等以空空导弹折叠舵为研究对象,从理论上解释了折叠舵受载的合理性[4];甄文强等对导弹横向折叠翼展开过程进行研究,建立了展开过程的数学模型、动力学仿真模型,并开展了地面试验研究[5]。
产品可靠性的定义是指在规定的条件下,在规定的时间内,完成规定功能的能力。刘吉军等人2009年就在《四川兵工学报》上发表过关于无线电导航系统可靠性的指数型寿命数据评估的文章[6];张建国、苏多对空间柔性机构建立了动力学微分方程,对展开机构的运动可靠性进行了分析与仿真[7]。刘飞、陈文华等利用Monte Carlo模拟计算方法计算得到导弹折叠展开机构工作可靠性[8];于卫东等人提出一种采用模糊故障树分析法研究舰空导弹系统可靠性的方法[9]。叶豪杰等人针对成败型复杂系统进行可靠性评估时综合方法易混淆使用造成评估结果错误的问题,提出了确定几种常用综合方法适用条件和范围的分析方法[10]。李海军等人指出[11-12],弹射装置及其挂钩闭锁机构的性能关系到导弹能否快速、准确并且安全地被弹射,需要设计可靠的能够同时解锁的弹簧蓄能弹射装置闭锁机构及其挂钩的闭锁机构。
文中以折叠舵展开机构为研究对象,首先应用UG软件建立折叠舵几何模型,然后导入Adams中进行动力学仿真,得到展开机构的角度、角速度及角加速度。最后基于Adams/Insight与响应面法的抽样思想,对折叠舵进行展开时间失效的可靠性分析,得到了相应的可靠度与灵敏度数据。
1 折叠舵结构及工作原理
某型导弹折叠舵的折叠状态外形如图1,其内部结构简图如图2。图1所示为舵体折叠时上舵体与下舵体成一定角度,并通过初始锁锁定。机构收到展开指令后,初始锁解锁,气缸内的火药开始燃烧做功,推动活塞。折叠舵上下舵面之间通过动轴与定轴连接,活塞运动时可以拉动其中的动轴,如图2。两转轴之间具有偏心距,偏心距使两转轴受转动力矩的作用,带动上舵体展开。展开后期,终位锁插入上舵体上的销孔,至180°时舵体完全展开并锁定。

图1 折叠舵折叠状态外形
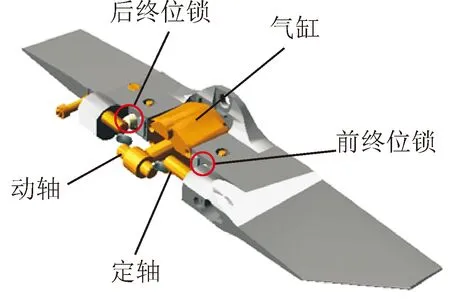
图2 折叠舵内部结构简图
2 折叠舵动力学仿真
2.1 动力学建模
文中利用UG建立折叠舵三维模型,然后导入Adams中建立动力学仿真模型,如图1所示。正确分析折叠舵受力情况是动力学模型仿真验证的关键,折叠舵舵面除受到气动力外,还受到火药做功产生的推力及舵面自重等。结构间的摩擦力等较小量值的力对模型机理验证结果产生的影响较小,不予考虑。建模时,正确施加迎风载荷(阻力)是重点。在理论和工程实践中常采用下式来简化计算迎风载荷[13]:
(1)
式中:C为气动阻力系数;ρ为空气密度;v为导弹相对气流速度;S为折叠机构(上舵体)的迎风面积;θ为上舵体展开角度。对于空空导弹,导弹发射或折叠机构展开的瞬间,导弹具有的速度近似等于载机的速度。
迎风载荷以分布力的形式作用于舵面,文中处理时将其等效成集中力,作用点位于上舵体几何中心。将建好的几何模型导入Adams/view中,定义各零件材料属性,并依据折叠舵工作原理定义零件间的约束、接触、驱动及运动副间的关系,建立符合实际的虚拟样机简化模型。
2.2 动力学仿真分析
折叠舵的运动仿真过程主要包括3个阶段:1)初始锁解锁;2)上舵体展开;3)终位锁锁止。其中第一个阶段由输入命令控制,仿真中不予考虑。第三个阶段伴随第二个阶段进行,上舵体展开结束时,终位锁锁止过程同时结束。
在Adams/simulation中设定仿真时间及仿真步数,仿真开始。进入Adams后处理模块,如图3~图5所示,给出了机构展开时上舵体展开的角度、角速度及角加速度随时间(s)的变化曲线图。
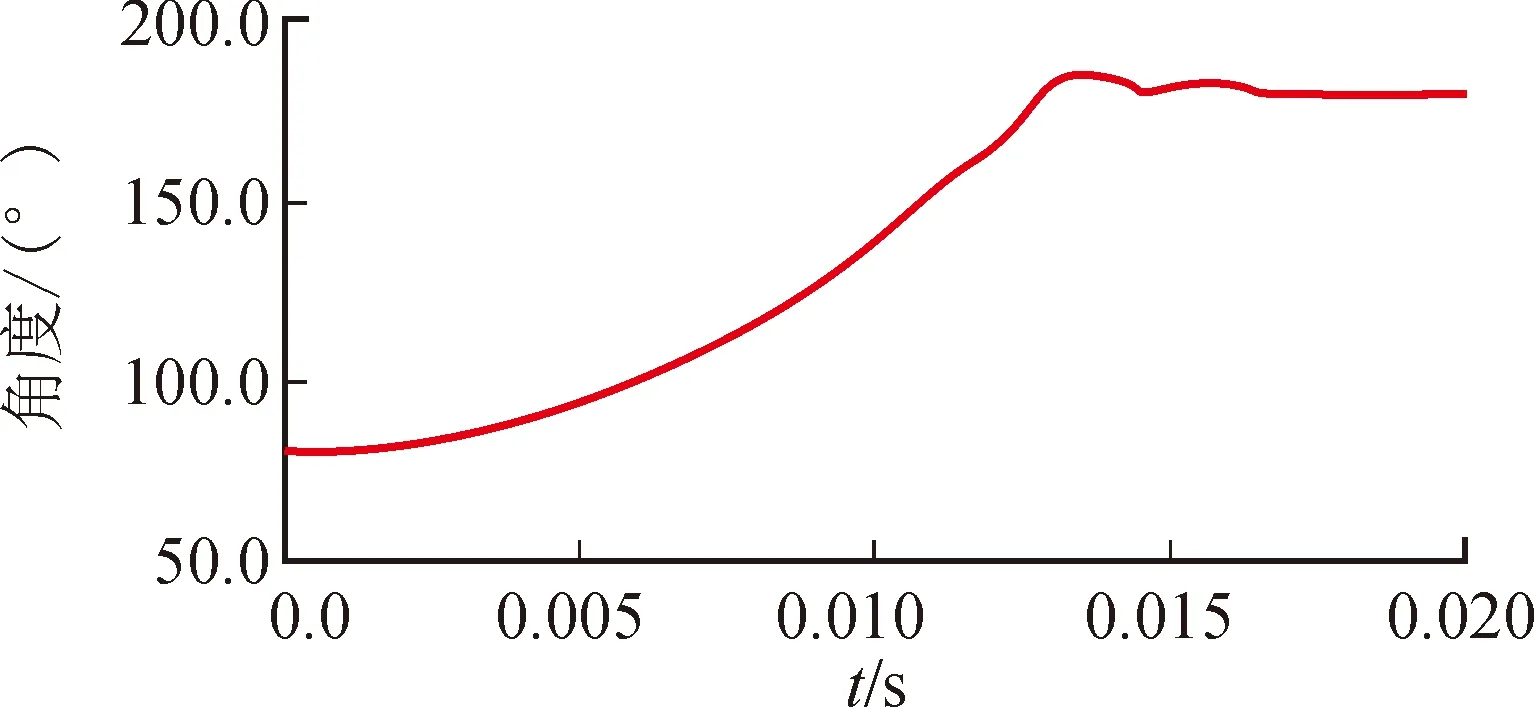
图3 上舵体展开角度变化曲线图

图4 上舵体展开角速度变化曲线图
由图3~图5中的曲线可以看出:展开指令发出后,上舵体平稳展开;展开即将结束时,出现微小振动,上舵体最终锁止在展开位置处。折叠舵动力学仿真结果表明:该折叠机构结构紧凑、可折叠、节约储存空间,有效满足了载机携带更多导弹的需求,符合工程实际;同时,折叠舵虚拟样机运行稳定,展开到位准确,可以为折叠舵物理样机的制造与改进提供一定的技术支持。
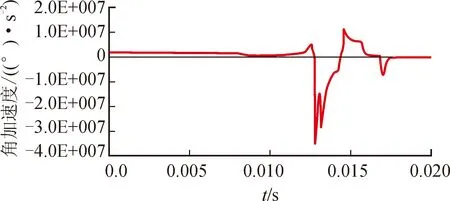
图5 上舵体展开角加速度变化曲线图
3 折叠舵可靠性建模
3.1 失效模式及随机变量
一般情况下,导弹翼面或舵面在整个展开过程会遇到两种极端情况:满载和空载。文中的可靠性分析工作针对满载情况展开。
满载时,折叠舵所受气动载荷做负功。若载荷过大,可能造成展开迟滞,甚至不能展开的极端情况。机构规定的满载时极限展开时间为20 ms,文中以展开时间失效为失效模式对机构进行可靠性分析:当展开时间超过规定时间或无法展开时,认为展开失败。另外,满载情况下引起展开时间失效的随机因素众多,变量选取过多会使得机构可靠性分析复杂,也不便于构造功能函数。因此文中选取满载情况下机构中相对重要的3处动摩擦因数作为随机变量。
3.2 模型参数化及试验设计
对模型进行参数化和试验设计是为了得到实验样本数据以便拟合得到响应面函数,即功能函数。
3.2.1 试验抽样方法及响应面函数选取
试验设计需要进行抽样,选定试验点。文中抽样思想借助于响应面法。从响应面法的基本原理可以看到,响应面法的实现过程中应该确定实验样本点的抽取方式。目前的取点方式主要有:Bucher设计、两水平因子设计、中心复合设计等,图6给出了二维情况下三种取点方式的抽样示意图。偏离距离一般取为f倍基本变量x的标准差σxi,f称为插值系数,一般取为1~3。文中综合3种抽样方式进行抽样。
结合经验以及工程实践,文中采用不含交叉项的二次多项式作为响应面函数形式,该多项式较好的折中了计算工作量与计算精度。由于响应面法已使隐式极限状态方程显式化,因此可以采用任何一种可靠性方法来计算可靠度及灵敏度,如Monte Carlo法。

图6 Bucher设计、两水平因子及中心复合设计抽样示意图
3.2.2 随机变量参数化
文中选取前后两组终位锁的锁销与上舵体之间的动摩擦因数、活塞与气缸壁之间的动摩擦因数这3个变量进行参数化。考虑到折叠舵的不对称性以及制造设计误差,在舵体展开时两组终位锁受到力的大小必然不同,因此需要将前后终位锁设计为独立的随机变量。在Adams/view中的Design Exploration版块中对变量进行参数化,分别将其命名为DV_suoqian、DV_suohou和DV_huosai。表1给出了各变量的均值(抽样中心)xi、标准差σxi以及插值系数f。
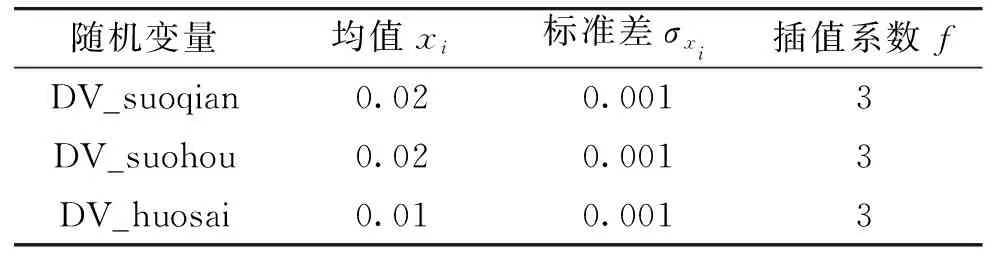
表1 随机变量基本数据及抽样插值系数
3.2.3 Adams试验设计
在Adams/Design Exploration版块可以进行试验设计,该板块可以用仿真试验代替实际的物理样机试验。给定设计变量的实验样本点后,利用Adams试验设计进行循环仿真,便可以得到需要的展开时间试验数据,表2给出了试验设计完成后前十组试验数据。

表2 仿真得到的部分数据 ms
3.3 功能函数和极限状态方程
3.3.1 功能函数的确定
分别设DV_huosai、DV_suoqian、DV_suohou值为x1、x2、x3,设展开时间值为y,选取不含交叉项的二次多项式作为响应面函数:
(2)
应用MATLAB结合最小二乘法对假设多项式进行拟合,拟合结果如表3所示。

表3 最小二乘法拟合结果
将结果代入式(2),得功能函数为:
(3)
3.3.2 极限状态方程
按要求折叠舵在满载情况下展开时间不能超过20 ms,否则认为失效,由此定义折叠舵基于展开时间失效的极限状态方程为:
gi(x1,x2,x3)=T-ti(x1,x2,x3)
(4)
式中:ti为折叠机构实际展开时间,即功能函数值,i为第i次仿真,T为规定的极限展开时间(20 ms)。若gi<0,即认为折叠机构展开失败。
4 可靠性计算分析
4.1 可靠度计算
极限状态方程确定后,利用Monte Carlo法进行可靠度计算,文中研究对象的失效模式为单失效模式。假设x1、x2、x3均服从正态分布,利用MATLAB进行循环抽样并依据可靠度公式计算,得到模拟仿真100 000次后的机构可靠度各项指标,如表4所示。
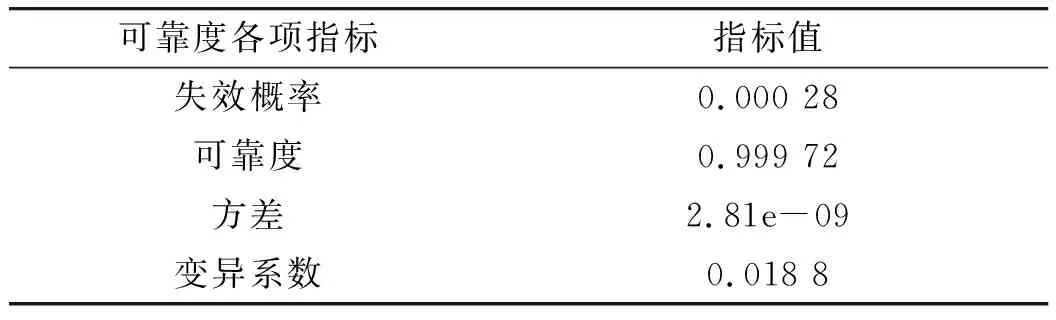
表4 可靠度各项指标
由表4可知,考虑机构3处动摩擦为影响参数时,折叠机构在满载情况下的展开时间失效概率为0.000 28,可靠度为0.999 72,可靠度较高;同时失效概率方差为2.81e-09,说明算法较为可靠。
4.2 灵敏度计算
依据Monte Carlo可靠性灵敏度分析方法,利用MATLAB进行循环抽样并依据灵敏度公式计算,得到机构各参数均值与方差的灵敏度结果如表5所示。
表5中Sa,Sb分别表示随机变量DV_suoqian、DV_suohou,Sc表示DV_huosai;1表示均值灵敏度,2表示方差灵敏度。由表5可知,在该折叠舵机构中,活塞与气缸壁之间动摩擦因数(DV_huosai)的均值灵敏度和方差灵敏度都大于其余两个随机变量的值,说明该参数对展开时间影响更大,为关键参数。同时Sc1值为负,说明DV_huosai变量的均值与可靠度成负相关,即均值越小,机构的展开可靠度越高。

表5 各项参数均值及方差灵敏度值
5 结论
1)文中以某型导弹折叠舵展开机构为研究对象:设计模型虚拟样机,进行动力学仿真分析,样机运行稳定,展开到位准确。结果验证了折叠机构体积小、结构紧凑、可折叠、节约储存空间,有效满足了载机携带更多导弹的需求。
2)以前后终位锁的锁销与上舵体之间的动摩擦因数和活塞与气缸壁之间的动摩擦因数为随机变量,以展开时间失效为失效模式,对折叠机构进行可靠性分析,结果表明机构可靠性水平较高,运行安全。
3)活塞与气缸壁之间的动摩擦因数为关键参数,相比于其它两处的动摩擦因数对展开时间影响更大,在今后设计中应重点优化。
