基于改进Memetic算法的区域防空优化部署方法*
2018-02-21陈西成
陈西成,文 童,刘 曙
(空军工程大学防空反导学院,西安 710051)
0 引言
区域防空的布防范围大,需掩护的群体较多,并且不同掩护目标的重要程度也不同,传统的将区域防空优化部署作为组合优化问题时,得到的部署方案在实际的防空作战中难以满足某些重要掩护目标的防空需求[1]。针对区域防空导弹部署问题,国内外学者进行了大量的研究[2-7],文献[5]建立兵力优化分配的数学模型,并对传统遗传算法改进,取得良好的部署效果。文献[6]以抗击效果为目标,建立多种类型防空导弹的混合部署优化模型。文献[7]综合考虑掩护能力和保卫目标重要度,建立以掩护价值为优化目标的区域防空部署优化模型。
以上研究大多是将区域防空部署作为组合优化问题建立求解模型,并从总体角度出发构建防空阵地网。但是从总体角度得到的部署方案在实际的防空作战中难以满足某些重要掩护目标的防空需求。因此在总体部署的基础上需对某些重点掩护目标增强火力分配。
因此,文中从总体出发进行区域防空导弹优化部署的同时,为保证重要掩护群的防空需求,提出局部部署与全局部署相结合的优化部署方法。区别于覆盖面积等单一的部署指标,将火力覆盖均匀度和拦截纵深作为优化建立部署模型。最后针对文中建立的模型,采取Memetic算法求解,选取差分进化算法[7]作为全局搜索算法,结合Baldwin效应[8]加大局部搜索成功个体的被学习概率,改进算法易陷入局部最优的问题。
1 区域防空部署问题分析
1.1 区域防空的特点分析
图1为某一防空区域的简化示意图,防区由防御中心A和重要掩护目标B、C和D组成,它们分别代表市区、机场、火车站、渡口等。在进行防空部署时可将市区A作为部署中心重点防护,同时对B、C和D这些可能会存在防空导弹火力防护不足的重要点状对象加强火力补充。

图1 防空区域简化示意图
1.2 防空导弹火力杀伤区描述
防空导弹火力杀伤区,表示部署的所有火力单元杀伤区组合后的杀伤目标空域,有关防空导弹杀伤区参数的描述如图2所示。

图2 线形部署三个防空导弹火力单元的火力区
图2中,拦截正面宽度L,是指垂直来袭方向连续的火力区最大宽度,拦截纵深h,是指在来袭方向上火力区的长度。目的就是为了得到大拦截宽度、长拦截纵深的防空导弹部署方案。
2 区域防空部署优化模型
2.1 部署阵地数学描述
防空部署可分为圆形部署、扇形部署、方形部署等,扇形部署能够判断敌武器来袭方向[9],从而集中主要兵力部署在可能的空袭主要方向。文中将进攻范围化分为不同区域,作为防御侧重的主要依据[9]。防空部署阵地离散网格化处理如图3所示。

图3 防区网格化示意图
图3中,网格中每个交点Pij=(θij,ρij)代表部署选样点,ρij表示待部署阵地距中心点的距离,θij表示方位角度。网格的分割根据防空地域的大小和部署的需求决定,并且要考虑防空武器的最小部署间距,网格的划分应使得备选位置间的距离大于最小部署间距。
2.2 优化目标
在防空部署中并不是“杀伤区的重叠次数越多越好”,某一方向过多的杀伤区重叠会造成资源的浪费[10]。文中选取火力覆盖均匀度和火力拦截纵深为优化目标[11]。
2.2.1 防空导弹火力覆盖能力

(1)


图4 目标杀伤区飞行距离计算示意图
在图4中,OA为防空导弹A部署点距区域中心的距离;Rmax和Rmin分别代表防空导弹的杀伤区远界和杀伤区近界:θ1代表OA和OD的夹角;θ2代表OA与OF的夹角;θ3表示最大航路角。
当θ1=θ2=0时,
(2)
当0≤θ2≤θ1时,
(3)
当θ3≤θ1≤θ2时,
(4)
(5)
2.2.2 防空导弹火力拦截纵深能力

(6)
所有防空导弹单元在整个防空区域的纵深性可以用式(7)的目标函数进行描述。
(7)
2.3 约束条件

(8)
2)地理环境约束:dxk表示该型号防空导弹距区域防空的中心距离;S表示不适合部署防空导弹的地域,dxmin表示防空导弹最小配置间距。
dxk≥l
zij∉S
dxkxk-1≥dxmin
(9)
3)重点方向拦截纵深要求:以区域中心的ω方向上要加强拦截能力。Zωi表示所有导弹在ωi方向形成的拦截纵深之和,Zmin表示最小拦截纵深。
(10)
2.4 优化模型
综上所述,根据区域防空导弹部署的战术需求,优化目标为保证拦截纵深不小于给定值的前提下,使得防空覆盖均匀度最大,模型如下所示:
minF=min{-fcov+min(fzs)}
(11)
(12)
3 Memetic算法设计
Memetic算法[12]是一种基于种群的全局搜索和基于个体的局部启发式搜索的结合体,具有很强的寻优能力和普适性。特别是在具有多极值特性的优化问题中,取得了很好的效果,针对文中模型对算法进行改进,改进思路如下。
3.1 个体编码
为保证能够在优化部署的同时满足重点地域加强火力防护的要求,采取多层编码方式如下式。
X=[x1,x2,…,xk,y1,y2,…,yk]
xi表示待部署阵地位置,对应防区网格矩阵的一维化的序号,yi代表的是防空导弹型号。将部署位置和导弹类型分开编码有利于分别优化部署位置和导弹分配。为确保s个重要地域获得防护,在初始化编码时需要固定染色体的前s位的数值。
3.2 基于学习率的变异操作
Baldwin效应中,个体学习到的好的性状无法通过基因遗传给后代,因此需引导种群发生与该性状相关的变异[8]。通过引导种群其他个体向好的个体学习并增加学习的概率来影响种群进化的方向。
以个体适应度值的倒数作为个体被种群学习的概率,被学习率li(t)通过式(13)产生。
(13)
式中:fi,s(t)表示个体本身的适应度,fi,ls(t)表示进行局部搜索之后所得适应度值,ω为缩放因子,取值为1。
在新一轮迭代中,算法按式(14)进行变异操作:
Vi,G=Xr1,G+Fi(Xr2,G-Xr3,G)
(15)
Xr1,G根据li(t)采用轮盘赌算法从全体种群中随机选取。
3.3 选择操作
若对所有个体均进行局部搜索,会产生不必要的运算代价;但若只对极少数精英个体实施局部搜索,则仅会对算法性能产生细微影响。由于种群中优质个体比其它个体更能代表种群的发展方向,因此对优质个体进行较多局部搜索而对较差的个体实施较少的局部搜索,有利于减少算法运算代价,提高搜索速度。同时为了避免过多运算代价,每次迭代中仅对部分较少个体实施局部搜索,数量为λ·NP(0<λ<1)。
经实验对比、验证,依概率pi(t)(求解最小值问题)从种群中挑选出较优个体进行模式搜索。
(15)
式中λ取值为0.5;函数示意图如下:

图5 pi(t)取值示意图
根据式(15)可以得出,当个体的适应度值为fbest(t)时,其被选中进行模式搜索的概率最大,为λ。
图5中横坐标代表某一代个体的适应度值,fbest(t)、favg(t)和fworst(t)分别表示这一代中最好的个体(设定中求最优适应度个体为求解最小值问题,即fbest(t)位于坐标轴的最左边),平均值和最差个体的坐标点。纵坐标代表个体被选中参与局部搜索的概率,函数为个体的适应度值跟被选中进行局部搜索的概率之间的关系。
3.4 步长自适应局部搜索算子
BMDE将简化的模式搜索作为局部搜索算子添入Memetic差分进化算法框架中[13]。对需要实施局部搜索的个体分别进行一次探测移动和一次模式移动。
探测移动从某点xk出发,依次在坐标轴e1,e2,…,eD上加减步长α,进行探测性移动;保留被探测点中适应度值最优个体xk′。若f(xk′)
模式移动按照式(16)进行:
xk+1=xk+β(xk+1-xk)
(16)
BMDE中β取0.5。
文中提出一种步长自适应策略,利用成功进行模式搜索个体的经验指导新一代个体的步长选择。BMDE中,每个个体进行模式搜索的初始步长取值如下:
αi,G=Norm(μG,0.1)
(17)
式中:αi,G是第G代种群中第μG个个体Xi,G使用的初始步长,服从均值为μG,标准差为0.1的正态分布。μG采用如下递推更新策略:
μG,lp=ημG+(1-η)mean(SG)
(18)
式中:η为松弛因子,取固定值0.5;mean(·)表示指数为1.5的幂均值;SG为第G代个体中成功进行模式搜索时所用α值的集合;μG的初值μ0取0.1。
4 MATLAB求解结果
现对以城区A为中心,极角120度范围,极径为200 km内的防空区域进行防空优化部署。防区内存在的重要掩护目标有机场A和B、火车站C。河域D为不适合部署防空导弹地域,现有防空导弹性能参数如表1所示。根据区域防空部署的要求,在部署优化时,要保证在距区域中心线正负20°内的最低火力拦截纵深达到150 km,并且总火力杀伤纵深最低的要求不小于1 000 km。

为验证所提方法的有效性,将文中提出的BMDE与标准DE和文献[14]提出的改进DE算法进行比较。各算法参数设置如下:
1)DE/rand/1/bin:F=0.7,CR=0.5.
2)SaDE:LP=50.
3)BMDE:F=0.7,CR=0.5.
设置种群规模为150,最大迭代次数为300。将三种算法分别独立运行10次,截取最终运行结果如表2所示。
算法运行最优解适应度曲线对比如图5所示,结合表2数据可以看出,文中提出的BMDE收敛速度快、搜索精度高;通过与传统的DE和改进的DE算法比较,验证了文中提出的BMDE在解决防空优化部署问题中的优越性。图6给出了通过BMDE运行得到的一个区域防空部署结果示意图。由图6可以看出,应用文中提出的模型和算法,能够在区域部署阵地中形成紧密衔接的防空火力网,并且完成了重点掩护目标的防空区火力强度的要求。
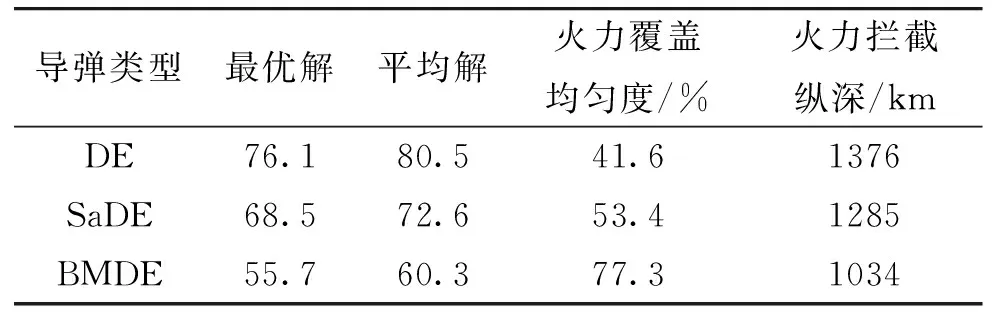
表2 算法性能对比

图6 适应度值收敛对比曲线

图7 区域防空部署结果示意图
5 结论
针对区域防空优化部署问题,提出对重要掩护地区加强火力分配的部署方案,分析区域防空问题并对杀伤区进行了相关描述,将问题抽象为简单扇形防空阵地优化部署问题。建立以防空火力覆盖度和火力拦截纵深为目标的优化部署模型。构造了基于差分进化的Memetic算法,对Baldwin效应进行了创新应用,改进了算法的性能。通过仿真实验,验证了文中模型的可行性与提出算法的有效性。
