无量纲参数滚动轴承长相关故障趋势预测
2018-02-20李宇飞宋万清陈剑雪
李宇飞,宋万清,陈剑雪
(上海工程技术大学 电子电气工程学院,上海 201620)
滚动轴承的故障很多时候不是突然出现的,存在一个从磨损到故障的缓变过程[1]。故障趋势预测对于实现机械设备的故障预警和预报、保障长期安全运行、减低维修费用和提高使用率具有重大的意义。故障预测的2个基本问题是:机械运行状态和故障趋势特征量的提取方法;根据故障特征序列特性进行的趋势预测方法。
目前故障趋势特征量主要有:基于数学形态谱的趋势预测特征提取[2]、基于循环平稳度的趋势预测特征提取[3]、基于经验模态分解的趋势预测特征提取[4]和基于无量纲参数的趋势特征提取[5]。形态谱的理论基础为数学形态学,其从物体形态的角度出发,发现信号的变化情况,能明显反映信号较小的变化,但计算速度跟不上,不适用于实时监测;循环平稳度是利用刚开始出现故障时时域波形出现周期趋势这一特征被提出的,但随着故障程度的加重和复杂性的变强,循环平稳性变差且分析过于耗时;经验模态分解自身存在端点效应,需进行优化提高精度,复杂性较高。因此,本文提取稳定性强、精度高的无量纲参数作为振动趋势预测的特征值。故障特征序列的预测有:基于模型的故障趋势预测方法、基于人工智能的趋势预测[6]方法、基于支持向量机的趋势预测[7]方法。模型预测没有陷入局部极小值而带来的精度问题;也不用担心样本的选择质量问题。
近年来无量纲幅域参数越来越受到关注,如波形指标、峰值指标、裕度指标、峭度指标[8-9]。它们对幅值能力变化不是很敏感,与机器工作条件关系不大,但是对设备故障足够敏感[10],并且计算简单,便于在线应用。由于轴承的故障类型和程度不同,这些无量纲参数对故障的敏感程度各不相同,一般都会将多种无量纲参数及有量纲参数相结合使用,才能更准确地判断故障有无及故障的发展趋势。
但是,传统的无量纲幅域参数仍是与能量有关的指标。与能量有关的指标会受到剧烈的工况负荷变化的干扰,或者因为信号能量变化不明显而失去故障特征量的意义。为了克服传统的信号波形无量纲参数仍与能量有关或者与能量无关但只能定性分析的缺点,基于时域波形统计分析,构建了几个新的对能量不敏感的无量纲幅域参数:重复性描述因子、相似性描述因子和跳跃性描述因子[11]。它们能定量分析与故障有关的波形形状信息,能更好地反映变负荷下的轴承故障发展趋势。
1 轴承振动的跳跃性描述因子
基于整周期采样,轴承的振动波形常呈现跳跃性,随着故障的恶化,波形跳跃性也发生改变,波形跳跃性的本质是波形的幅值调制。为了能定量描述跳跃性,分别对平均重复波形和分段波形数据{x11,x12,…,x1m;…;xn1,xn2,…,xnm}取x11、x12、…、x1m中的极小值xmin=x1p,1<p<m,均值方差则跳跃性描述因子Jf=Dx。
以实验平台中ZA-2115双列球轴承为研究对象,进行为期7天的全寿命周期振动信号采集。提取振动烈度[12]、相似性因子和敏感性因子,通过分析与比较选择合适预测的量纲参数。实验平台包括了一个电机、加速度计和热电偶。轴承中经为2.825英寸,滚珠数为16,同一轴上安装4个轴承。主轴转速为2 000 r/min,带有恒定负载,通过DAQ-6062数据采集卡每隔10分钟采集一次数据,采样频率为20 kHz,采样点数为20 480,以此获得全寿命周期7天从轴承完好到发生故障的振动数据,提取轴承全寿命周期振动信号进行无量纲参数构建。实验装置如图1所示[13]。
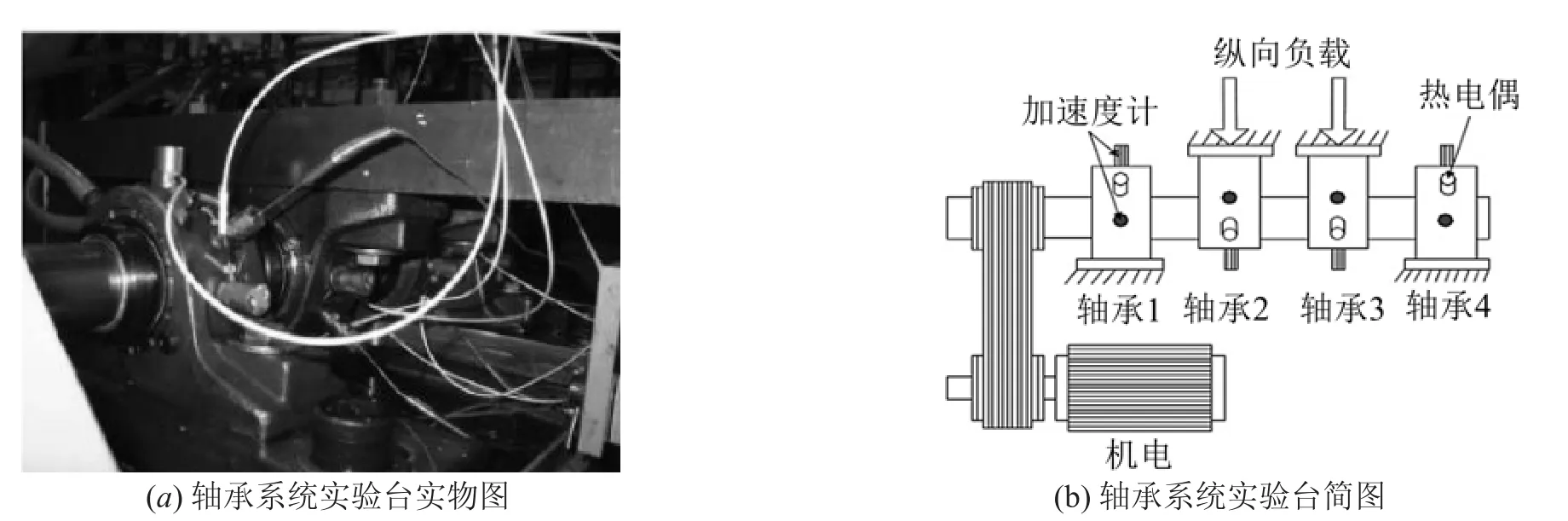
图1 滚动轴承故障诊断实验平台
2 不同无量纲参数缓变故障序列
实现故障预警的量纲参数需满足两个条件:
(1)在无故障的情况下,量纲参数不因滚动轴承振动信号的非线性、非平稳特性而产生较大的波动,具有相对稳定性。
(2)量纲参数需对轴承早期故障具有一定的敏感性,且有迹可循,能够进行故障早期预警与预测。
根据实验2以及参考文献[13]里的数据可得,振动烈度值、相似因子值和跳跃性因子值在7 000 min左右均发生较为明显的变化,满足故障预警条件。
图2中红线左侧7 000 min前,振动烈度值在1.8左右,7 000 min后出现微弱波动,但不够明显。仅在故障后期才出现烈度值大于1.8的较大波动,由此说明振动烈度对早期故障存在不敏感性或者对故障信息存在滞后性,不适合作为故障预警信息。
新无量纲参数即图3所示的相似性因子和图4所示的跳跃性因子均在故障早期开始了较为明显的变化,但随着故障程度的加深,相似性因子由正常状态下的1.73左右变化为故障出现后展现出一种随机性与无规律性,同样不适合作为预测对象。而跳跃性因子在正常状态下的趋近于0,到故障出现后开始逐步增大,反映出滚动轴承具有故障恶化的趋势,说明跳跃性因子同时具有无故障时的相对稳定性和对故障的敏感性,可以作为故障预测的实施依据。
3 趋势预测长相关模型
为了更好地对轴承故障趋势进行预测分析,所建模型应考虑轴承故障信号特性。一方面,轴承振动信号时间序列呈现非线性、非平稳特性,导致从中提取的无量纲特征量序列也呈非线性发展的趋势;另一方面,轴承振动特征量因其目前状态与过去状态的相关度,还会具有短相关性或长相关性。基于此,我们将采用非线性时间序列预测模型:自回归积分滑动平均模型(Autoregressive Integrated Moving Average Model,ARIMA)和分数差分自回归求和移动平均模型(Fractionally Autoregressive Integrated Moving Average Model,FARIMA),其中,ARIMA能通过整数阶差分提取时间序列的发展趋势,较准确地预测具有短相关性的特征量发展趋势,FARIMA则是在ARIMA的基础上,针对长相关序列进行分数阶的差分,防止过差分去除长记忆低频成分。最后,文中将利用MIX-ARMA把ARIMA和FARIMA相融合,使MIX-ARMA模型既适用于短相关时间序列,又适用于长相关时间序列。
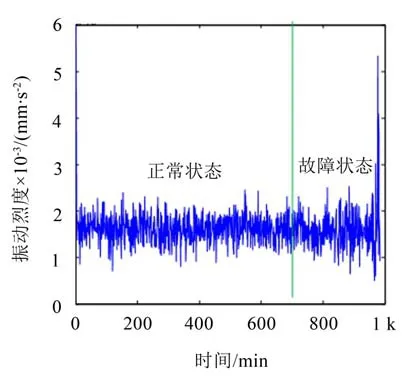
图2 振动烈度趋势图

图3 相似性因子趋势图
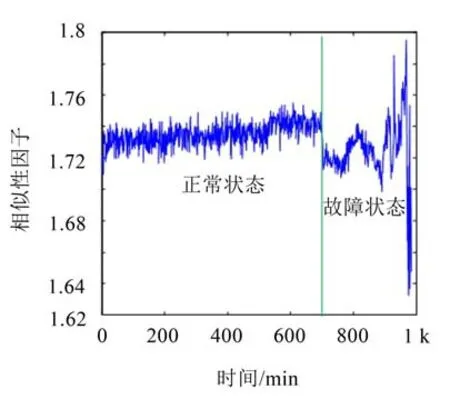
图4 跳跃性因子趋势图
3.1 FARIMA长相关预测模型
FARIMA(p,d,q)是ARIMA(p,d,q)的一种扩展形式,其可被分离为分数差分噪声FARIMA(0,d,0)和ARMA(p,d)2部分[14],可表示为
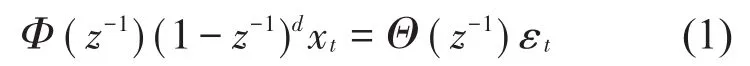
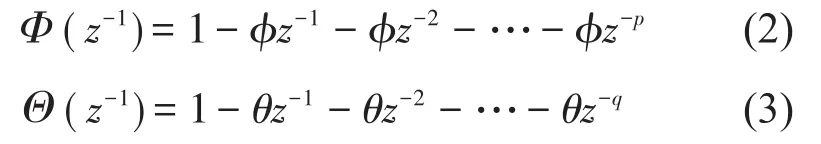
针对具有长相关特性的数据,为了防止利用ARIMA(p,d,q)过度差分消除长相关趋势,FARIMA(p,d,q)中的差分阶数d∈(-0.5,0.5)。FARIMA(p,d,q)的预测过程与ARIMA(p,d,q)相似,首先利用分数阶对原始数据进行差分,然后用传统的ARMA模型进行分析和模型结构识别,使用最小二乘法确定模型参数,最后进行预测结果的分析,因此,重点是判断目标数据是否具有长相关特性和差分阶数d的计算。
对于一平稳时间序列x(t),-∞<t<+∞,利用rxx(τ)=E[x(t)x(t+τ)]定义其自相关函数,当rxx(τ)可积时,x(t)被称为短相关时间序列[15],且

而当rxx(τ)不可积时,x(t)满足长相关特性[16],且
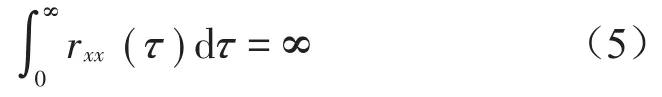
自相关函数的渐进式还可表示为

其中:c>0为常数,0<β<1。
检验时间序列的长相关性一般采用Hurst参数估计方法[17],当Hurst指数取值为0.5<H<1时,就可表明此时间序列具有长相关特性,且H越接近于1,序列的相似程度越大。除此之外,Hurst指数H与FARIMA(p,d,q)中d存在H=d+0.5的关系,因此,还可通过H来计算差分阶数的值。目前,重标极差法(R/S分析)[18]是计算Hurst指数最常用的方法,其在具有较快运算速度的同时还保持了计算的精度。
3.2 MIX-ARMA自适应预测模型
由ARIMA和FARIMA分析可知,二者的基础模型都为ARMA,仅在数据预处理差分阶段存在区别,这样就可以将二者合并为MIX-ARMA(p,d,q)自适应预测模型,定义其模型为
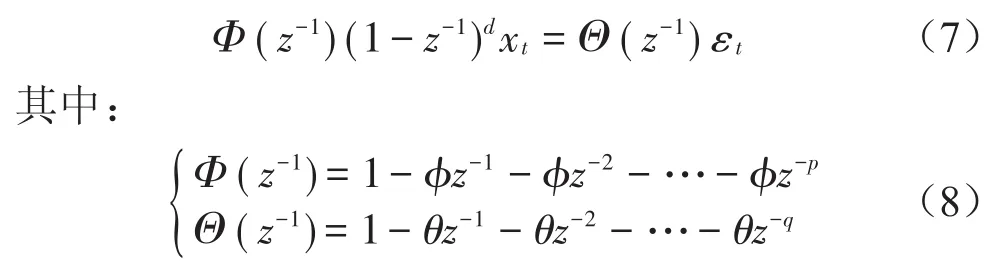
式(7)所定义的模型与FARIMA模型相似,只是差分阶数d∈(-0.5,0.5)⋃{0,1,2,…,n},也就是差分系数d既可以取到分数,又可以取到整数,说明此模型既适用于短相关时间序列,也适用于长相关时间序列。由式(8)可发现,MIX-FARIMA的建模过程需确定3个模型参数:差分阶数d、自回归阶数p、移动平均阶数q。差分阶数d的取值同样适用Hurst指数的计算过程,总平均预测误差APEZ则使用改进交叉核实准则

其中:Q=5,m=0.1N。改进的交叉核实准则是将时间序列的历史数据根据预测需求分成两部分,前一部分用于建立模型,后一部分用于检测模型的预测误差。其中后一部分数据又被分为Q段,每段长m。用每一段数据检测模型的预测误差,并且在一段数据被检测完之后,该段数据被加入前一段部分数据中,作为建立模型的新数据。最终取每一段预测误差的平均值APEZ作为模型的预测误差。使得预测误差APEZ最小的参数即为最优模型参数。
4 不同无量纲参数缓变故障序列
为了选取更适合的预测模型,利用上述介绍的Hurst指数法先对将要预测的时间序列进行分析。图5和图6代表利用R/S法分别对轴承振动信号和跳跃性因子序列所做的自相似曲线,其中,轴承振动信号的Hurst指数为0.647 7,同时由振动信号提取的跳跃性因子的Hurst指数为0.894 1,两者的H值都大于判断标准0.5。可见,一般的轴承振动信号除了具有非线性、非平稳性外,还具有长相关性。我们发现轴承振动信号具有自相似特性。自相似序列的典型特征是具有长相关性,即轴承振动信号在较长的时间范围内都具有相似性,且这特性不能被忽略[19],通过对H值的计算,更是定量确定了研究对象的长相关性。
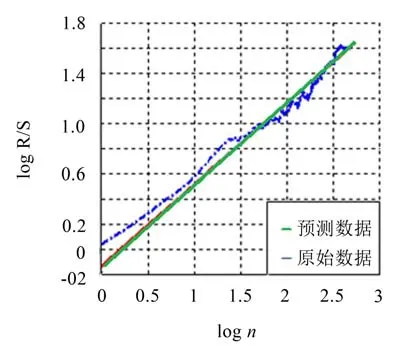
图5 轴承振动信号的R/S
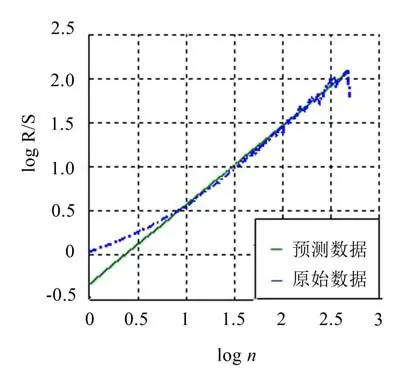
图6 跳跃性因子的R/S
在进行预测时,选取跳跃性因子前700个数据用于建模,后280个数据作为预测的比较值,利用ARIMA和FARIMA模型。ARIMA对数据进行1阶差分,FARIMA对数据进行d=0.394 1阶差分,图7则显示了原始数据和差分后数据对比图。
从图中可以明显看出,当对原始数据进行1阶差分时,轴承发生故障之后的抖动数据被过度平滑化,大部分特性被抹灭,其Hurst指数也被降到0.5以下,不再具备长相关特性。而被分数差分后的数据,相比较1阶差分,保留了大部分的数据抖动内容,其Hurst指数同样保持在0.5以上,此数据仍具备长相关性。
针对跳跃性因子,利用ARIMA和FARIMA模型所得预测结果已显示在图8和图9中,当此时间序列具有长相关性时,FARIMA模型和MIX-ARIMA模型是相同的。
针对具有长相关性的跳跃性因子进行建模预测分析,从第700个数据开始进行预测,每次预测10个数据后,将实际的这10个数加入到前一部分序列中,作为新的模型预测数据,最终将所有的预测数据与实际数据对比,从图形上看,FARIMA模型的预测值非线性趋势更强,更贴近真实数据,由表1的对比结果发现,无论是平均绝对误差还是平均相对误差,FARIMA模型的预测精度都比ARIMA模型高,可见,当跳跃性因子呈现长相关特性时,FARIMA模型更适合。
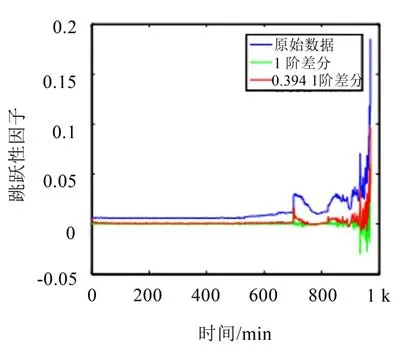
图7 差分结果图
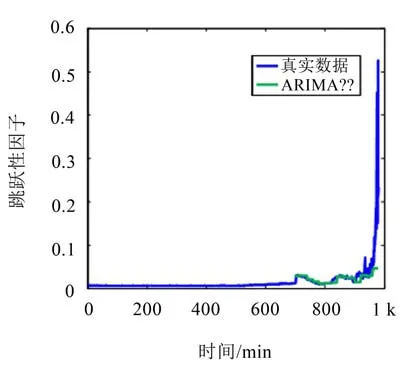
图8 ARIMA模型预测对比

图9 FARIMA模型预测对比

表1 ARIMA与FARIMA预测对比
5 结语
针对轴承故障时间序列的预测问题,寻求解决这一问题的方法:选择量纲参数指标作为轴承振动信号趋势预测特征值,在传统有量纲的振动烈度值无法满足量纲预警条件下,提出使用新的无量纲参数——重复性因子、相似性因子和跳跃性因子,最终选择最符合预警条件的跳跃性因子作为趋势预测特征值;通过研究发现,预测模型ARIMA和FARIMA两者都基于ARMA模型,因此将短相关时间序列模型ARIMA和长相关时间序列模型FARIMA相结合,提出MIX-ARMA自适应预测模型,其可以基于时间序列的相关性自动选择合适的模型;基于轴承跳跃性因子序列的长相关性,对其进行FARIMA模型的预测建立,与ARIMA模型相比,其具有精度更高和自适应的优点。
